均勻重力場中質點在光滑圓柱面上的撓曲線運動
李 力
(重慶清華中學,重慶 400054)
在理論力學和分析力學課程里,通常研究質點的平面曲線運動。這些做平面曲線運動的質點,多數被約束在二維平面上,也有一些被約束在二維曲面上。約束在二維曲面上發生的一般的空間撓曲線運動,卻很少涉及。空間曲線不僅有彎曲的性質,而且還有扭轉從而離開平面形式的性質。前一性質用曲率描述,后一性質則用撓率刻畫。平面曲線的撓率恒等于零,反之,撓率恒等于零的曲線必是平面曲線。所謂撓曲線,就是撓率不恒為零的曲線[1],這種空間撓曲線運動的處理,不可避免地要用到更多的數學方法,比如微分幾何的曲線、曲面論,某些特殊函數的知識等。
本文研究了均勻重力場中的質點在光滑圓柱面上的撓曲線運動,用牛頓定律或拉格朗日方程推導質點的運動微分方程,然后解得質點脫離圓柱面的位置滿足的方程以及脫離前的運動時間,最后導出用橢圓積分表示的撓曲線運動軌跡的參數解析表達式。
1 質點在光滑圓柱面上的運動微分方程
在如圖1所示的光滑1/4圓柱面以及圓柱坐標系(ρ,φ,z)中,質點的初位置在圓柱面的最上端A(R,0,0),初速度v0在過A點的水平切面內,與Oz軸夾角為α,沿Oz、Oy軸的分速度分別為v1,v2。顯然有初始條件?z0=v1=v0cosα,R?φ0=v2=v0sinα,即
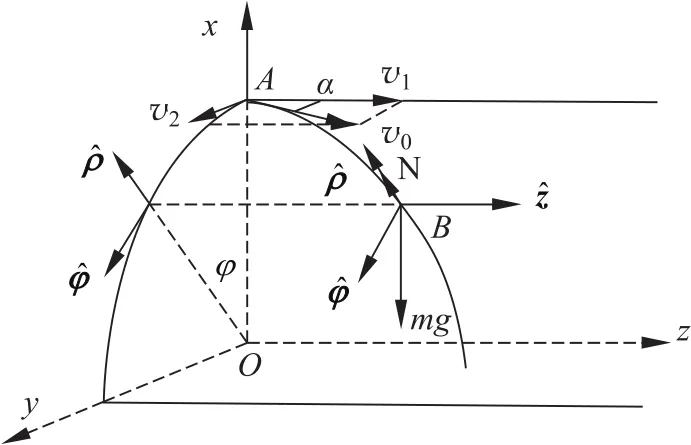
圖1 質點在光滑圓柱面上的撓曲運動
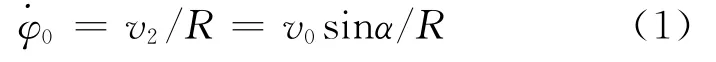
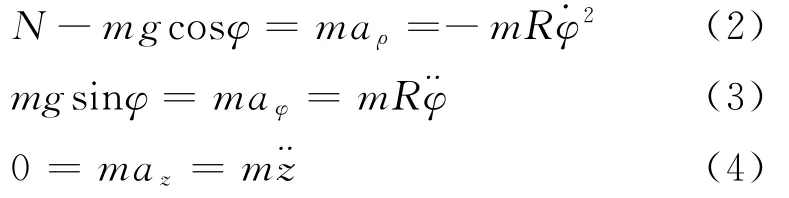
順便指出,用拉格朗日方程也可以簡便地推導出(3)、(4)兩式,此處不再贅述。
2 z和?φ的推導
由式(4)積分,并考慮初始條件,得?z=v1,故
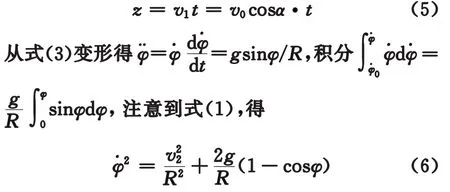
因?φ>0,故取
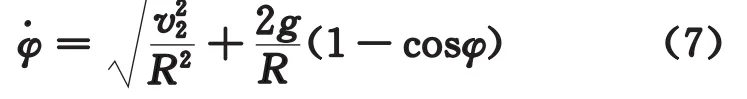
3 脫離位置與脫離時間
將式(6)代入式(2),并令 N=0、φ=φm,有
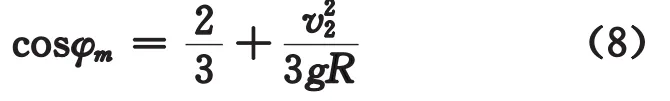
由于在A點不脫離圓柱面,須v2< g R,從而式(3)右端另外,若v=0,則脫離2位置cosφm=,這正是理論力學課程中熟悉的結論[3]。
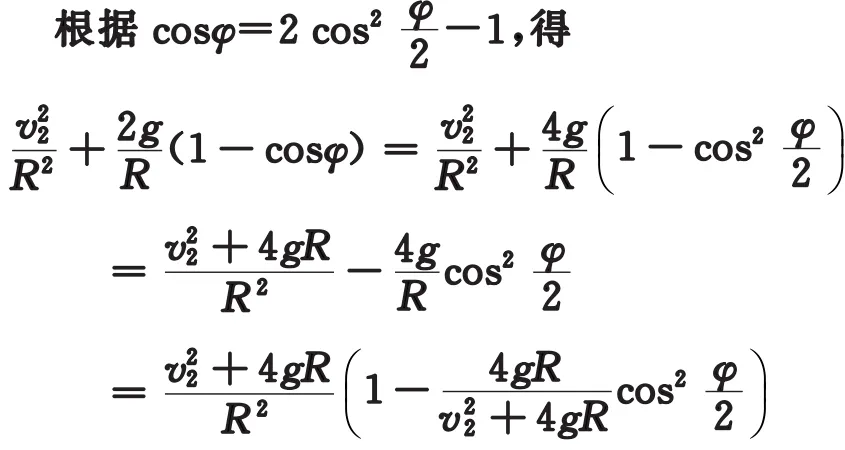
故式(7)化為

得到脫離時間
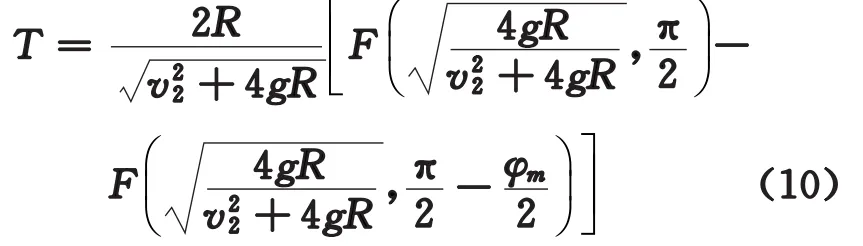
其中F(k,φ)是勒讓德第一類橢圓積分[4],即而φm由式(8)定出。
4 運動軌跡方程的解析表達式
為了得到在圓柱面上的運動軌跡方程,只需在式(10)中作代換T→t,φm→φ,并同式(5)聯立,即得用橢圓積分表示的撓曲線運動軌跡的參數解析表達式為
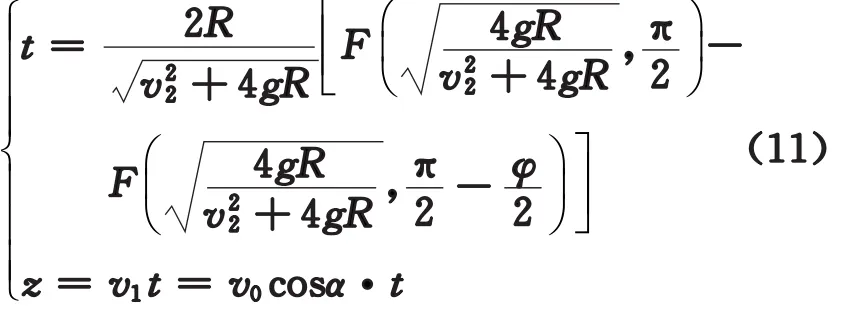
或者直接寫成
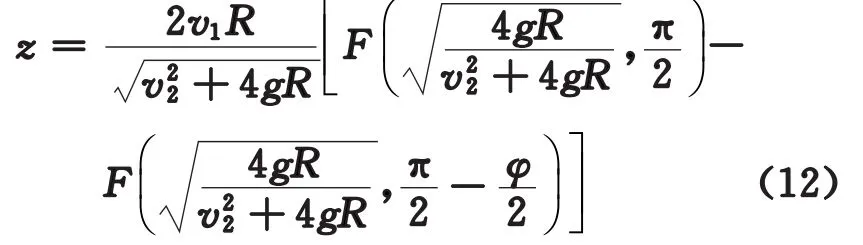
按照微分幾何曲線論[1],得到運動軌跡在直角坐標系中以時間t為參數的曲線表達式為

如果以z為參數,則曲線的參數方程可寫為
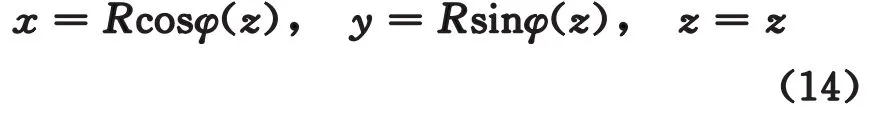
其中φ(t),φ(z)分別是由式(11)和式(12)所定義的φ與t、φ與z之間的函數關系。
5 結語
研究均勻重力場中的質點在光滑圓柱面上的撓曲線運動,有一定的理論意義和應用價值。本文用牛頓定律或拉格朗日方程推導質點的運動微分方程式(2)~(4),然后解得質點脫離圓柱面的位置滿足的方程(8)以及脫離前的運動時間式(10),最后導出用橢圓積分表示的撓曲線運動軌跡的解析參數表達式(11)~(14)。
因為圓柱面上過A點的沿v0方向的平面截線是橢圓,而式(11)~(14)表明運動軌跡并非橢圓,所以質點做撓曲線運動;又由變分法可知,圓柱面上的測地線(即短程線)是螺旋線[5],故質點的運動軌跡也不是測地線。另外,用微分幾何可以證明,在只受曲面法向約束力時,質點必沿測地線運動[6],而我們討論的本問題還要考慮均勻重力場的作用,因此更為復雜。由此可以看出,均勻重力場中的質點,在任意形狀的光滑曲面上的空間撓曲線運動,求解起來有相當的難度,一般而言是不容易得到或者根本不存在解析表達式的。

