基于同步壓縮小波法的行波故障測距應用研究

陳雅芳，蔡世翔（.廣州中光電氣科技有限公司，廣東 廣州 50660；.廣東電網公司云浮供電局，廣東 云浮 57300）

0 引 言

隨著電力系統規模的逐漸加大，國民對用電可靠性和運行穩定性的要求越來越高。所以，要減少電力系統運行故障的發生，且需在電力系統發生故障后快速、準確地定位故障并排除故障。快速準確的故障測距定位是電力系統安全穩定運行的前提條件，可以有效提高線路巡線人員的工作效率，減小停電造成的各種經濟損失，具有重大的社會經濟效益[1]。行波測距不易受系統參數、線路負荷等外界條件干擾，定位速度迅速且測距精度較高，是近年來輸電線路故障測距的發展方向與研究熱點之一。

1 同步壓縮小波變換原理

小波分析被認為是在傅里葉分析基礎上的重大發展。它在時域和頻域都有很好的局部化特性，因此在計算機視覺、數據壓縮和信息編碼解析等眾多應用學科領域得到了廣泛應用。本文利用信號在不同尺度上小波變換的Lipschitz指數、模極大值來表征信號的突變特點，即利用信號的奇異性對電力線路行波故障測距進行研究和應用。

同步壓縮小波[2-3]支持信號重構，且時頻分辨率比傳統小波方法高，原理如下。

對于信號x(t)，它的傅里葉變換可表示為：

其中，ω代表角頻率，其反變換為：

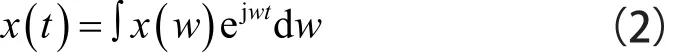
則信號x(t)可以表示為一組不同頻率的諧波之和。這種現象可以表述為式（3），對信號s(t)有：

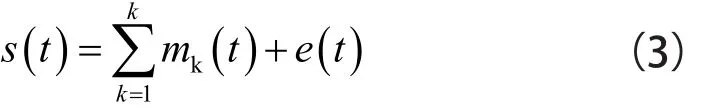
式中，mk(t)=Akcos(φ(t))表示第k個時變諧波成分，其中Ak(t)表示信號的瞬時振幅，φk(t)表示第k個諧波成分的瞬時相位；e(t)表示擾動或噪聲。

由相位求導得到瞬時頻率fk(t)：

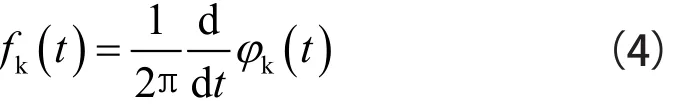
將小波變換重新計算至頻率域，得到：

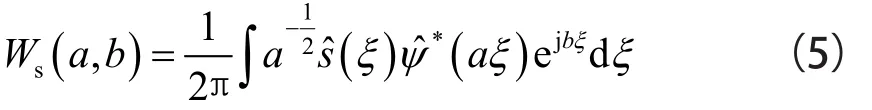
式中，a為尺度因子，b為時間平移因子，ξ為角頻率，ψ^( ξ) 為母小波的傅里葉變換。

將單一諧波信號s(t)=Acoswt進行小波變換，結果為：

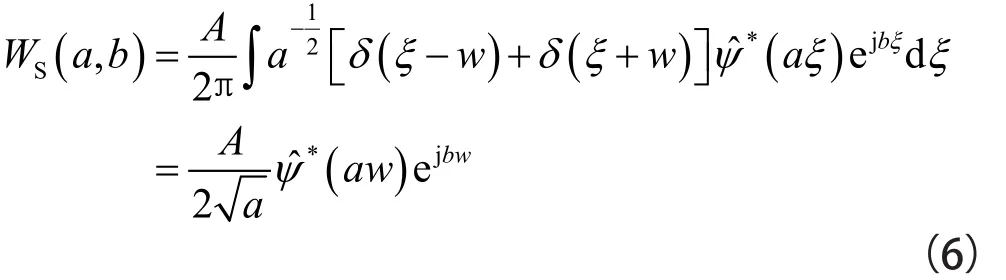
若母小波的主頻是w0，那么其小波系數譜理論上集中在尺度a=w0/w的位置，即母小波與子小波的頻率之比。實際上，即使小波系數在尺度方向存在擴散現象，但由于其相位是保持不變的，所以針對小波系數WS(a,b)可以計算其瞬時頻率：

其中，arg(·)為小波系數的相位。

同步壓縮小波變換是通過計算瞬時頻率，把小波系數從(b,a)投影到(b,ωs(a,b))。而對于離散情況，尺度坐標和頻率坐標都是離散值(Δak=ak-ak-1，Δwl=wlwl-1)。因此，同步壓縮小波變換的公式可以表示為[4]：

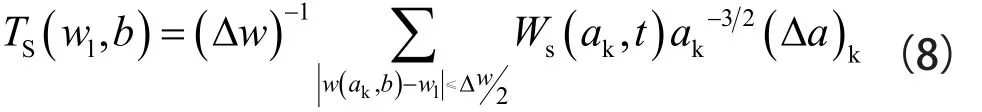
其中，ak為尺度坐標(k=1,2…)，wl為頻率坐標（l=1,2…）。

由于同步壓縮小波變換在頻率方向將復小波系數進行了重新排列，因此該過程是可逆的。將其進行逆變換，結果為：

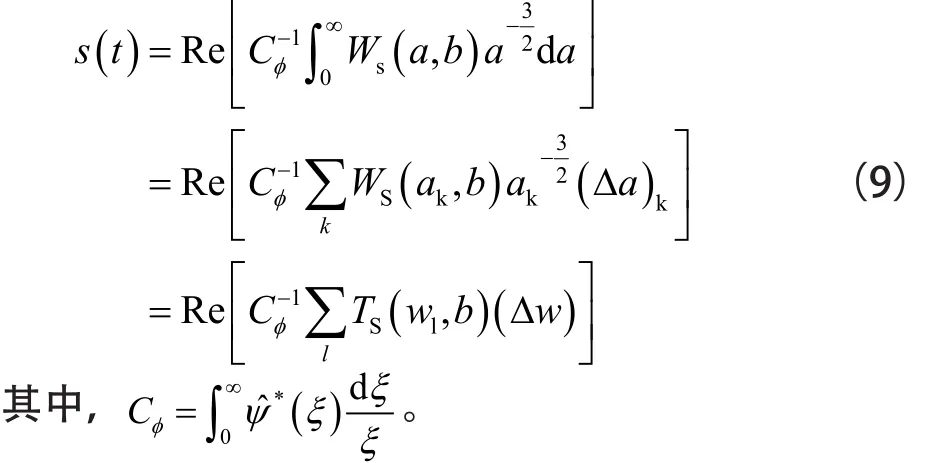
2 理論信號分析

首先對一組合成信號進行驗證分析，以驗證同步壓縮小波變換的高分辨率特性。合成信號波形如圖1所示，該信號是由一個頻率為50 Hz、幅值為1的正弦波和一個頻率為100 Hz、幅值為1的正弦波疊加而成。合成信號進行小波變換，結果如圖2所示。對合成信號進行同步壓縮小波變換，結果如圖3所示。對比以上兩種小波變換的結果可以看出，同步壓縮小波變換具有更高的分辨率。

圖1 合成信號波形

圖2 合成信號小波變換結果

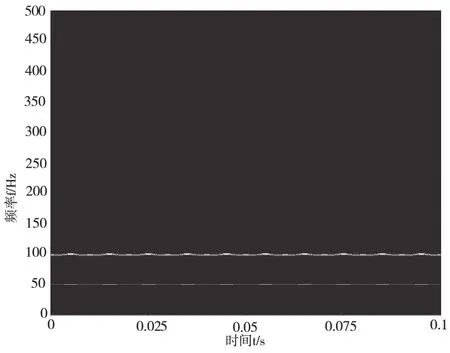
圖3 合成信號SWT結果

綜上分析，因為同步壓縮小波變換在數學上是可逆的，所以通過對信號的反變換可完全恢復處理前的原始信號。對信號的同步壓縮小波結果進行反變換，結果如圖4所示。可以看出，重構信號與變換前的原始信號基本重合，重構誤差很小[5]。

圖4 SWT反變換結果與原始信號

3 仿真分析

3.1 不含噪情況

為了驗證該方法對電力系統單相接地故障電壓數據分析的效果，在仿真軟件MATLAB上搭建了雙端線路模型M-N進行雙端行波測距。測距流程圖如圖5所示，M端電壓線模分量如圖6所示，M端α模分量SWT結果如圖7所示，對得到的SWT變換做反變換的結果如圖8所示。可見，結果基本與原始信號吻合，符合SWT的數學特性。

圖5 SWT雙端測距流程圖

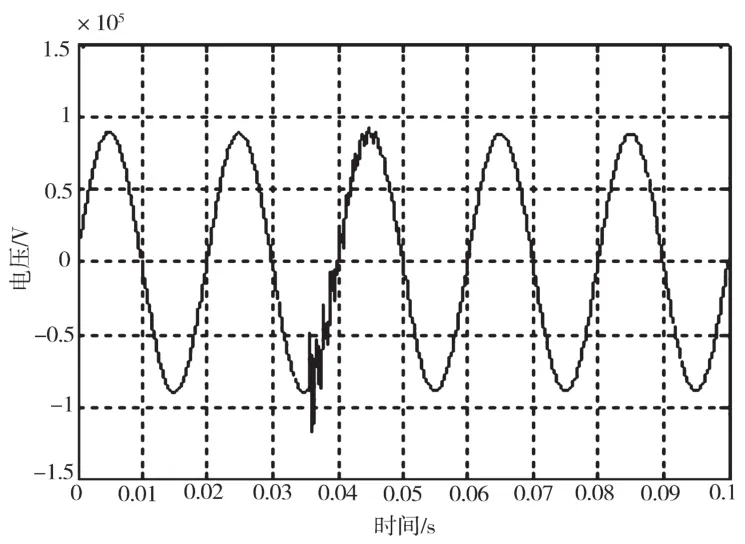
圖6 M端α模分量

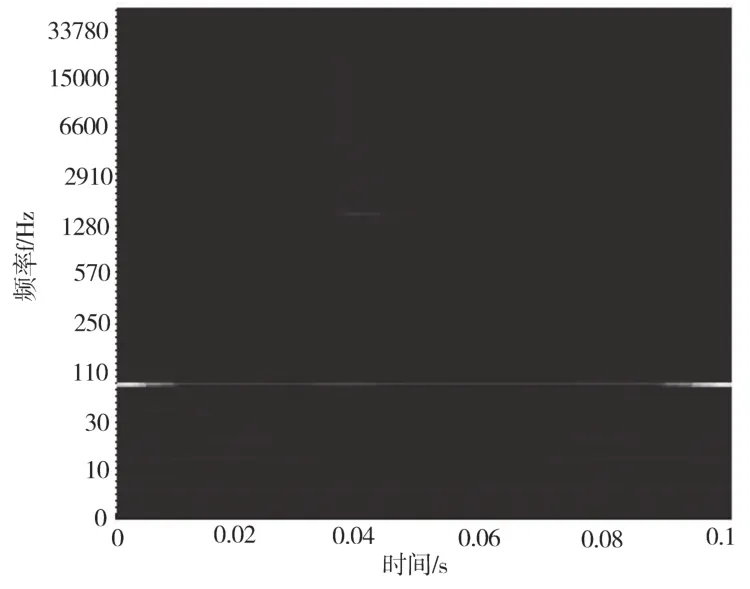
圖7 M端α模分量SWT結果

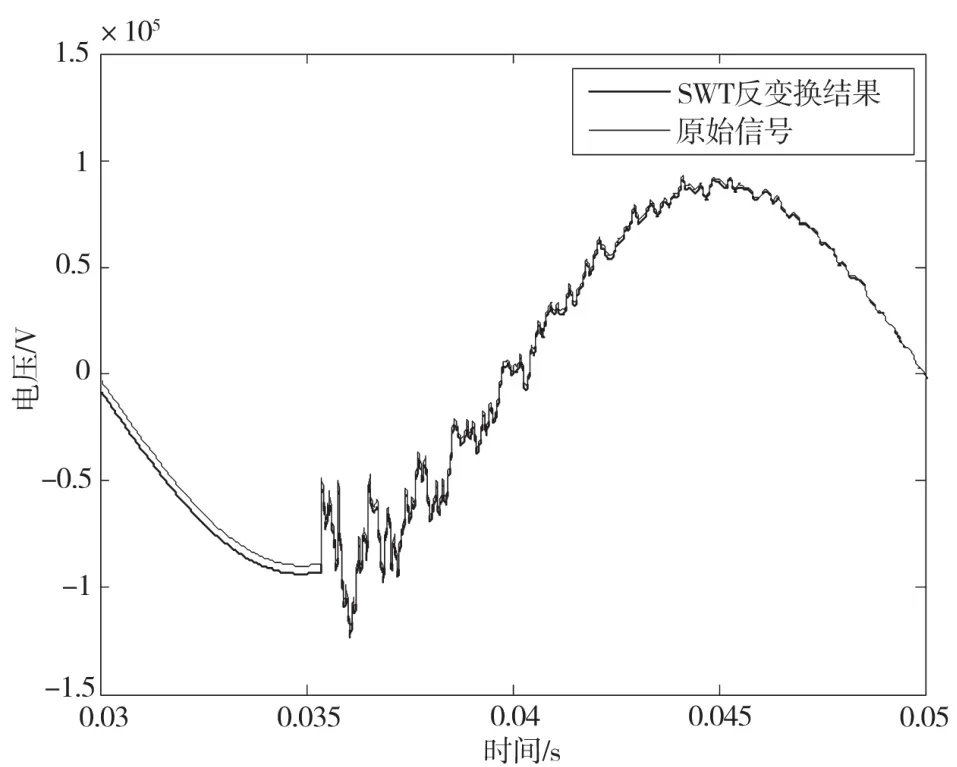
圖8 SWT反變換結果

得到四端的30 kHz故障行波分量波形，如圖9所示。

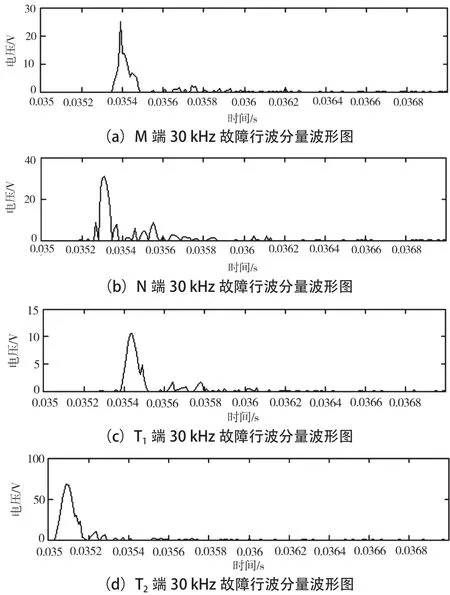
圖9 不同端30 kHz故障行波分量波形圖

得到M、N、T1和T2四端的初始行波波頭到達時 間 分 別 為 0.035 40 s、0.035 2 s、0.035 44 s和0.035 09 s。下面采用SWT的多端測距結果與小波變換（CWT）測距結果進行比較，結果如表1、表2所示。可見，SWT變換與CWT相比，測距精度與計算速度獲得了大幅提高。

3.2 含噪聲情況

在模型中附加40 dBW，對其線模分量進行SWT，結果如圖10所示。

最終得到的測距結果為25.18 km，誤差180 m，表示同步壓縮小波法可以準確定位故障位置。

表1 采用SWT的多端網絡故障測距仿真結果

表2 采用CWT的多端網絡故障測距仿真結果

圖10 不同端經SWT后的故障行波

4 結 論

本文采用同步壓縮小波變換對單相接地故障發生時產生的故障行波進行了時頻分析，并得到了最終的測距結果，發現同步壓縮小波變換可以較為準確地識別行波波頭，并定位故障點，取得了較好的分析效果。

[1] 嚴 鳳，楊奇遜，齊 鄭，等.基于行波理論的配電網故障定位方法的研究[J]. 中國電機工程學報，2004，24（9）：37-43.

[2] Montejo L A，Vidot-Vega A L.Synchrosqueezed Wavelet Transform for Frequency and Damping Identification from Noisy Signals[J].Smart Structures and Systems，2012，9（5）：441-459.

[3] 汪祥莉，王 斌，王文波，等.混沌干擾中基于同步擠壓小波變換的諧波信號提取方法[J].物理學報，2015，64（10）：100201.

[4] 秦 晅，宋維琪.基于同步壓縮變換微地震弱信號提取方法研究[J].石油物探，2016，55（1）：60-66.

[5] 覃 劍，吳成琦.利用小波變換的雙端行波測距新方法[J].中國電機工程學報，2000，20（8）：6-10.