基于置換理論的等級調制糾錯碼新構造方法*

張用宇

（中國人民解放軍91469部隊，北京 100841）

0 引 言

閃存（Flash Memory）是一種采用浮柵結構的長壽命非易失性存儲器[1]，即使在斷電情況下仍能保持所存儲的數據信息。置換碼是一種多進制糾錯碼。近年來，由于陸續發現了置換碼在電力線數據傳輸和多級閃存等領域的新應用[2-3]，置換碼重新引起了學者的關注。雖然閃存技術飛速發展，但仍然存在兩個問題制約其發展。一是閃存讀寫操作過程中電荷注入的問題，如過量注入導致的過度編程（單元注入電荷值高于目標電荷值）；二是數據的可靠性，如閃存中存儲的數據受到了電荷泄漏、數據保持問題、讀/寫干擾等影響而受到損壞。采用等級調制方案[4-6]可以避免閃存單元過度編程的風險，還可以降低電荷泄漏等噪聲引起的非對稱錯誤影響。當讀寫單元的電平值時，僅需要比較不同單元之間的電位值。當電位值向一個方向偏離時，它們的等級不會像絕對值受到影響。因此，等級調制可有效提高寫入速度，減少非對稱錯誤，提高數據可靠性。

因為閃存設備中產生錯誤的特殊性，所以RS碼、LDPC碼等差錯控制編碼方法不能有效糾正這些錯誤。基于置換理論的等級調制糾錯碼適合于多級閃存中多個單元電位值具有相同等級的等級調制糾錯方案。與置換碼[7-8]相比，基于置換理論的等級調制糾錯碼可以有效提高閃存的可靠性，達到較高的信息存儲率。

針對有限強度錯誤的研究，文獻[2，9]提出了等級調制糾錯碼的構造方法。在Chebychev度量下，Min-Zheng Shieh提出了直接和遞歸的多重置換碼構造方法[7]。在此基礎上，本文提出了兩種基于置換理論的等級調制糾錯碼的構造方法，一種是直接方法，即通過多重置換集進行直積運算得到；另一種是間接方法，即通過對已有多重置換集進行運算得到新的多重置換集，進而再進行直積運算構造出等級調制糾錯碼。

1 基本概念

對于正整數n∈?，設[]n表示集合{1,2,…,n}，SA是集合A的對稱群，即基數為n的集合A上所有置換的集合， []nS 簡記為nS。對于具有n個閃存單元的等級調制編碼，假設n個閃存記憶單元分別命名為1,2,,n…。每個單元的電平等級記為ic，其中i。n個閃存單元的排序為集合Sn上的一個置換，并設其中一個置換為一個閃存單元等級相對值由高到低的一個排列。設表示置換映射其中等級調制方法由編碼和譯碼兩個函數定義。編碼函數輸入信息a∈Q映射成一個置換譯碼函數D：nSQ→。由于置換f會被可能的擾動影響，影響后的置換記為f′，譯碼的目標是使()D fa′=。

定義一個多重集（Multiset）為：

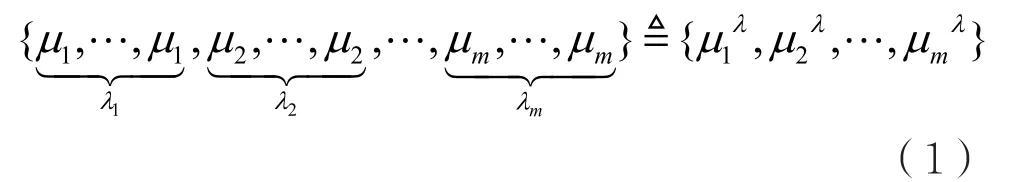
其中，且

考慮一種特殊的情況，令且則多重集變為：

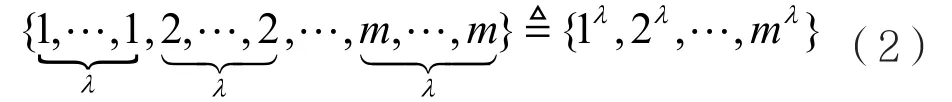
設是式（2）的對稱群，即式（2）所有置換的集合。

定義1 對于定義f與g之間的切比雪夫距離函數為：

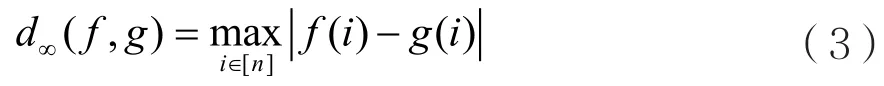
定義2 基于置換理論參數為(λ,n,d)的等級調制碼C定義為 Sn的子集，即其基數為C中碼字的個數，記為M，且對于所有,f gC∈，fg≠，有

2 構造方法

構造1 設,,mdλ∈?，nmλ=，2λ≥，對于

i∈[d]，令：

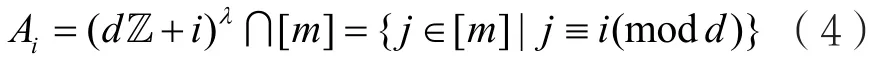
設是iA（[]id∈）的對稱群，構造多重置換碼的直積，即：

構造的碼C是Chebyshev度量下的一個基于置換理論的(,,)n dλ等級調制碼。

定理1 構造的(,,)n dλ等級調制碼的基數為：

證明：令,f gC∈是任意2個不同的碼字。對于i∈[n]，有由多重置換集Ai的定義，可知可得對于由Chebyshev距離函數定義可得：

因此，構造的碼C是一個(,,)n dλ多重置換碼。

由構造條件可知，d個多重集iA（[]id∈）是多重集的一個劃分，其中n=mλ。設正整數[]id∈，如果d不能整除m，每一個多重集iA（[]id∈）中元素的個數至多為如果d能整除m，每一個多重集中元素的個數都為在Ai個多重集中恰好有m (m odd)個多重集，其中每個多重集包含個元素。由于每個元素在對應的多重集中分別出現λ次，每個多重集中重復的個數為其余的個多重集，其中每個多重集包含個元素。考慮到每個元素的重復次數，每個多重集中重復的個數為因此，構造的(λ,n, d)等級調制碼的基數為：

例1：設正整數11m=，2λ=，3d=。由構造1中的定義可得對于表示 A 的對稱群，i即多重集iA上所有置換的集合。它在Chebyshev度量下的最小距離為 d = 3 。例如，當 i = 3 時，的基數為由構造方法1得到等級調制碼它在Chebyshev度量下的最小距離為 3d=，碼長即C是一個(2,22,3)等級調制碼。通過式（6）可得，碼C的基數M為571 536 000。

例2：設正整數12m=，2λ=，3d=。此時，d能整除m。由構造1中的定義可得

每一個多重集Ai包含8個元素，集合的基數都為2 520，在Chebyshev度量下的最小距離為d= 3 。由構造方法1得到等級調制碼其在Chebyshev度量下的最小距離為 3d= ，碼長即C是一個(2,24,3)等級調制碼。通過式（6），可得碼C的基數M為16 003 008 000。

構造2 設,,mkλ∈?，nmλ=，2λ≥，對于令：

定義運算：

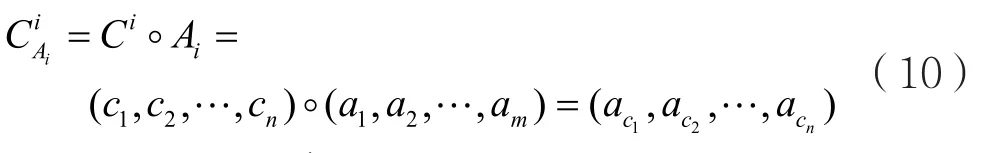
其中

構造碼字

定理2 構造的碼字C是一個基于置換理論的(,,)n dλ等級調制碼，其基數最小距離

證明：由構造方法容易得到碼字的長度nmλ=，等級調制碼C的基數大小

由構造2可知，是最小距離為ikd的多重置換集。令,f gC∈是任意2個不同的碼字，對于有是k的倍數。因此，最小距離

例3：設正整數7m=，2λ=，3k=。由構造2給出的方法可得到其基數13M=，22M= ，32M= 。設碼1

C是由構造1的方法得到的碼長最小距離12d=的(2,6,2)等級調制碼：

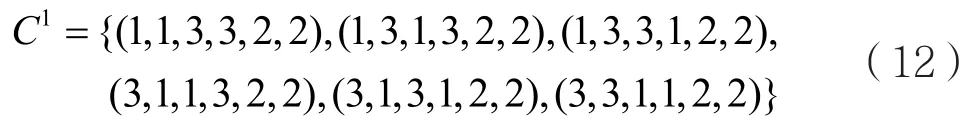
根據構造2的方法，中各碼字在集合1A上構成一個多重置換集即：

在Chebyshev度量下最小距離為 k d= 6 。1

同理，設碼2

C是由構造的方法得到的碼長最小距離d2=1的(2,4,1)等級調制碼：

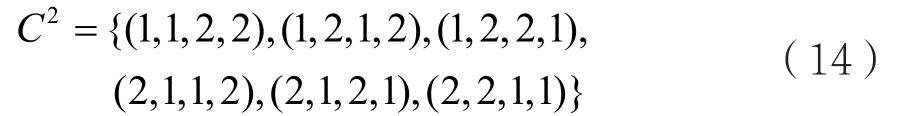
C2中各碼字在集合 A2上構成一個多重置換集

在Chebyshev度量下最小距離為 k d= 3 。2

設碼3C 是由構造的方法得到的碼長最小距離d3=1的(4,2,1)等級調制碼：

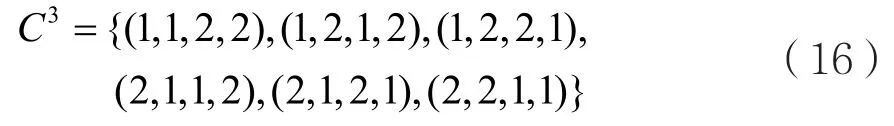
中各碼字在集合3A上構成一個多重置換集最小距離為的(2,14,3)等級調制碼C，其基數為：

在Chebyshev度量下最小距離為 k d= 3 。3

由提出的構造2的方法，可得到一個碼長為

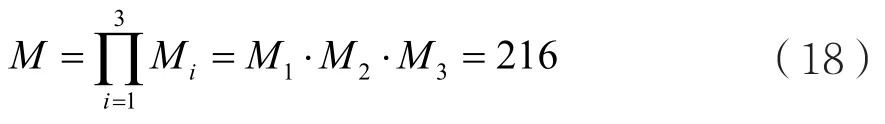
(2,14,3)等級調制碼C如表1所示。

表1 (2,14,3)等級調制碼C

3 結 語

閃存具有高性能、非易失性、能耗低和存儲容量大等優點。在多級閃存中，采用等級調制方案可有效克服閃存的有限強度錯誤。針對這一問題，基于多重置換理論提出了采用直積運算直接和間接等級調制糾錯碼的兩種構造方法，構造方法簡單直觀，易于編譯碼，并通過計算實例表明了構造方法的正確性。多重置換碼的研究對基于多重置換碼的等級調制方案的設計具有重要意義，在多級閃存和無線通信等領域可有效對抗信道中的脈沖噪聲、窄帶噪聲、背景噪聲和衰落等干擾。

[1] Cappelletti P,Golla C,Olivo P,et al.Flash Memories[M].Boston MA:Kluwer,1999.

[2] Tamo I,Schwatz M.Correcting Limited-magnitude Errors in the Rank-modulation Scheme[J].IEEE Transactions on Information Theory,2010,56(06):2551-2560.

[3] 慕建君,趙鵬,焦曉鵬.一種糾單個閃存單元移位錯誤的譯碼方法[J].西安電子科技大學學報(自然科學版),2016,43(06):51-55.

MU Jian-jun,ZHAO Peng,JIAO Xiao-peng.Decoding of Codes Correcting a Single Translocation Error for the Cell’s Level of Flash Memory[J].Journal of Xidian University,2016,43(06):51-55.

[4] Jiang A,Mateescu R,Schwartz M,et al.Rank Modulation for Flash Memories[J].IEEE Transactions on Information Theory,2009,55(06):2659-2673.

[5 Gabrys R,Yaakobi E,Farnoud F.Codes Correcting Erasures and Deletions for Rank Modulation[J].IEEE Communications Letters,2016,62(01):136-150.

[6] Holroyd A E.Perfect Snake-in-the-box Codes for Rank Modulation[J].IEEE Transactions on Information Theory,2017, 63(01):104-110.

[7] Shieh M Z,Tsai S C.Decoding Frequency Permutation Arrays under Chebyshev Distance[J].IEEE Transactions on Information Theory,2010,56(11):5730-5737.

[8] Liu X,Draper S C.LP-decodable Multipermutation Codes[J].IEEE Transactions on Information Theory,2016,62(04):1631-1648.

[9] Kl?ve T,Lin T T,Tsai S C,et al.Permutation Arrays under the Chebyshev Distance[J].IEEE Transactions on Information Theory,2010,56(06):2611-2617.