基于Simulink的跳頻通信系統的抗干擾性能分析*

王 欣，陶 杰，崔佩璋，胡建旺，孫慧賢

（陸軍工程大學石家莊校區，河北 石家莊 050000）

0 引 言

跳頻系統的抗干擾能力強，廣泛應用于軍隊和人們的日常生活。軍隊里各種電臺基本都有跳頻通信的功能，主要是為了躲避敵人搜索信號或者敵人對某一頻率的信號進行干擾。日常生活中，頻率資源有限，zigbee、WiFi和藍牙的頻率都在2.4 GHz，同時使用勢必會互相干擾。但是，它們都劃分了很多信道，會自動選擇干擾少的信道使用，即采用跳頻技術。可見，跳頻技術已經應用于生活和工作的方方面面，分析其原理和抗干擾性能將具有極其重要的意義。

1 跳頻通信系統原理

跳頻通信是指使發射機的載頻在一個信息碼元的時間內按照預定的規律離散地快速跳變，從而達到擴展頻譜的目的。載頻跳變的規律一般由偽碼控制頻率合成器生成。當跳頻序列值改變一次，載波頻率將跳變一次。信號調制到這些不同的頻率中，即形成跳頻信號[1]，然后進行傳輸。在接收端，用相同的偽隨機碼控制頻率合成器產生本振信號，接收端收到的信號與本振信號相乘，再經過中頻濾波得到穩定的中頻信號，最后經過解調恢復原始的信號。而其他的跳頻信號、干擾信號和噪聲，不可能與本地頻率合成器的信號混頻成固定的中頻，所以解跳時這些信號落在中頻濾波器通帶外，不會對有用信號的解調產生影響。

2 跳頻模型建立及主要模塊

2.1 基于Simulink的跳頻通信仿真模型

根據跳頻通信系統的基本原理，用Simulink對跳頻系統建立仿真模型。圖1為根據跳頻系統原理框圖在Simulink仿真平臺上搭建的FH/MFSK通信系統仿真模型。設置本跳頻系統為慢跳頻系統，即跳頻速率低于信息比特率，每跳可傳輸連續幾個比特率。信源為二進制隨機序列，數據速率為100 b/s，調制方式選用BFSK調制，BFSK頻率間隔為2 kHz，BFSK頻率點數為16個，跳頻速率為100跳/s，跳頻頻率間隔為100 kHz，信道為AWGN信道。

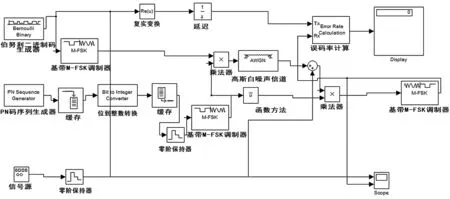
圖1 跳頻系統仿真模型

由設置的參數可以看出，此系統輸出的信號為100 kHz×16=1.6 MHz，頻率范圍為-0.8～0.8 MHz。如果仿真頻譜范圍達到-2～2 MHz，根據低通抽樣定理，采用頻率為4×10-7次/s。下面介紹它的主要模塊和參數設置。

2.2 信源模塊

如圖2所示，信源模塊采用Bernoulli BinaryGenerator模塊。因為要求的輸入數據速率為100 b/s，所以輸入一個數據需要0.01 s。設置參數時，采樣時間應為0.01 s。

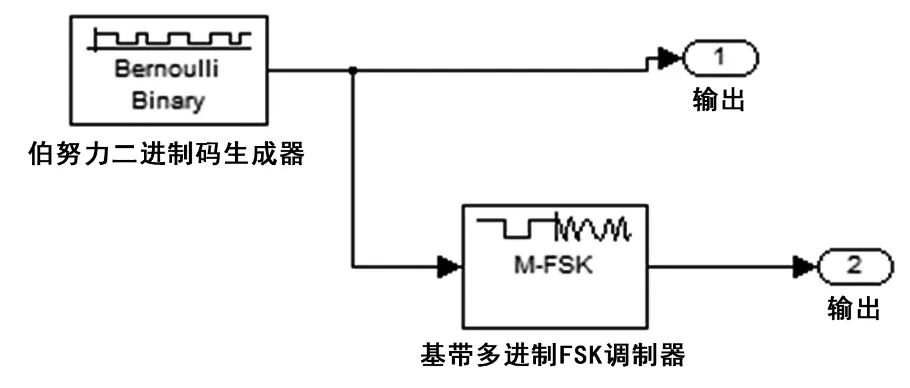
圖2 仿真系統中的信源子系統展開結果

2.3 BFSK調制/解調模塊

調制解調模塊采用M-FSK Modulator Baseband。此模塊中，設置M的值實現不同進制的頻移鍵控。如何實現輸出信號采樣率為4×10-7次/s？因為輸入數據速率為100 b/s，所以每個符號的采樣點應該是4×10-5，填到對應的每符號采樣點即可。

2.4 跳頻信號產生模塊

跳頻信號產生模塊如圖3所示。圖3中的跳頻信號的產生過程為：PN Sequence Generator產生的偽隨機碼為m序列，Buffer的作用是把輸入為一列的二進制序列變為4列二進制序列輸出，通過Bit to Integer Converter后變為一列十六進制整數。然后，通過解緩存器Unbuffer和零階采樣保持電路Zero-Order Hold，偽隨機序列發生器產生的二進制數轉變為十六進制的整數，饋送到M-FSK Modulator Baseband的控制輸入，從而輸出跳頻信號。

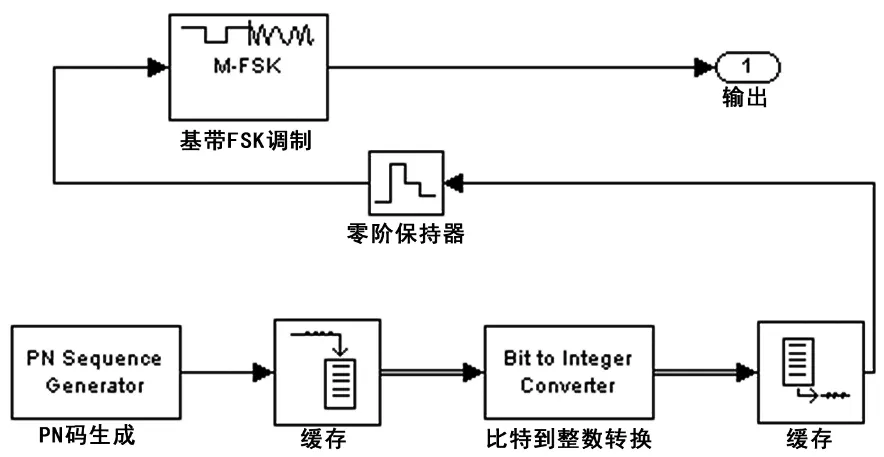
圖3 仿真系統跳頻子系統展開

2.5 跳頻通信系統的仿真結果

從圖4可以看出，系統各節點頻譜與理論基本符合，收發數據的波形基本一致。通過仿真波形可以看出，此仿真模型的建立是正確的。為了分析跳頻系統的抗噪聲性能，可以先分析其頻譜特征，進而分析其抗噪聲性能。圖5為信源信號頻譜，圖6為經過跳頻系統后的信號頻譜。通過分析跳頻通信系統的頻譜發現，其頻譜比信源信號頻譜展寬了，說明即使有干擾，由于信號頻譜展寬了，對信號的影響也會變小。對于不同的干擾，跳頻系統存在一定的抗噪聲性能。下面就典型干擾對跳頻系統的影響展開分析。

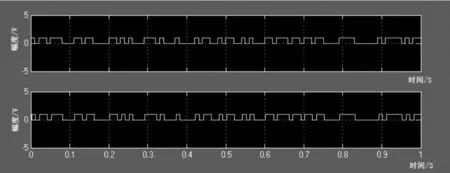
圖4 系統收發數據對比結果

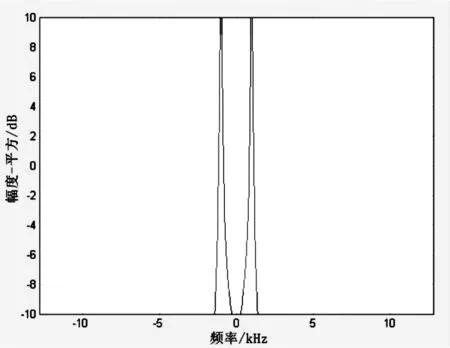
圖5 信源頻譜

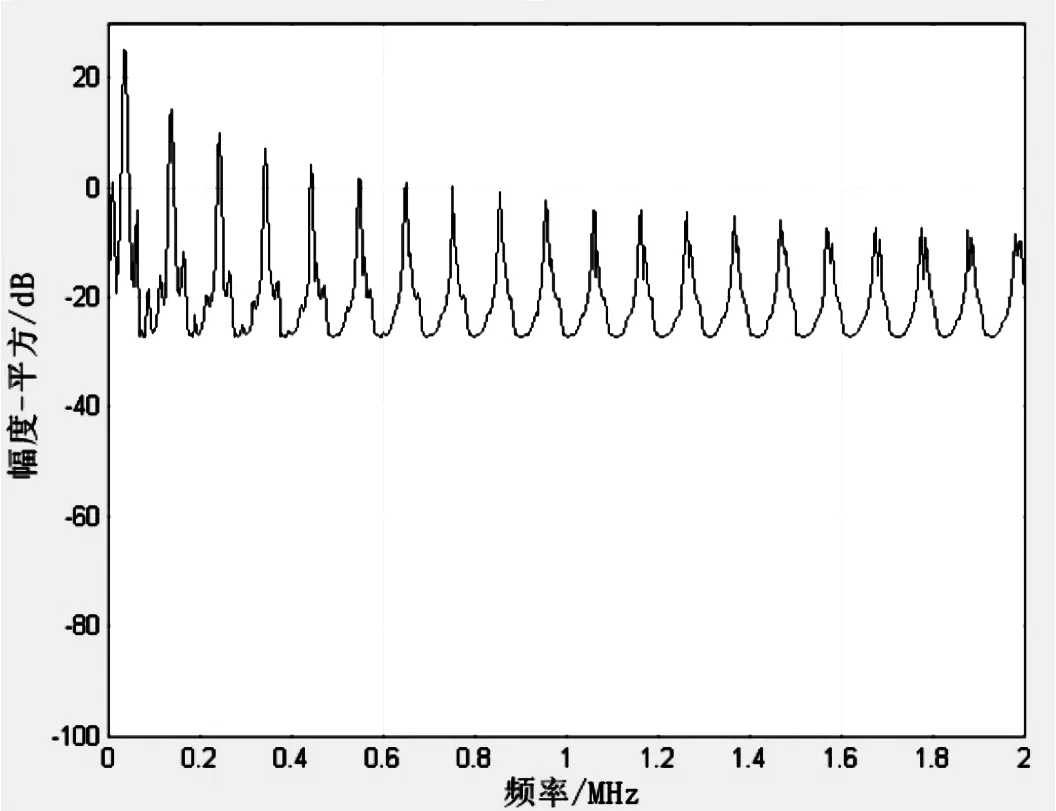
圖6 跳頻通信后輸出信號頻譜

3 典型干擾對跳頻系統的影響

跳頻通信是快速改變信號的頻率，使敵方無法偵查到有用信號。信號速度改變越快，敵方越不容易偵查到。但是，提高跳速，成本必定提高。綜合考慮各種性能與成本，下面分析寬頻帶干擾、單頻干擾和多頻干擾下的跳頻通信系統的抗干擾性能[2]。

3.1 寬頻帶干擾

寬頻帶干擾即全頻段干擾，利用Simulink中的加性高斯白噪聲AWGN模塊，將其疊加到信號上進行干擾。調整模塊中干信比的大小不同，此跳頻系統的誤碼率也不同。圖7為Matlab仿真得到的寬帶干擾頻譜。

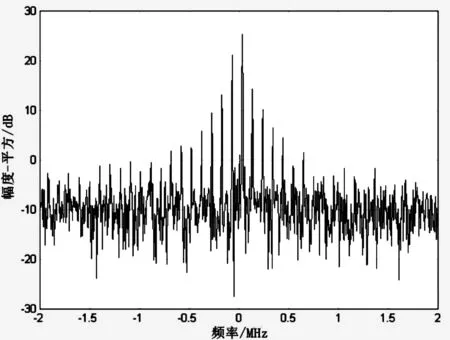
圖7 Matlab仿真下的寬帶干擾頻譜

其他參數設置不變的情況下，改變干信比的大小，得到如圖8所示的誤碼率干信比曲線結果。

由誤碼率曲線圖可知，全頻段干擾對通信系統的干擾效果非常明顯。當干信比上升時，誤碼率急劇上升。可以看出，干信比在0 dB時，誤碼率為10-2，一般的通信系統可以進行正常通信；當干信比高于7 dB時，誤碼率已經達到0.1，此時跳頻系統已經不能正常通信；當干信比為20 dB時，誤碼率已經接近0.5，此時系統已經完全無法通信。當然，全頻段干擾付出的代價必定也很大，需要設備更復雜、功率更高。

3.2 單頻干擾

單頻干擾也稱點頻干擾，即只有一個頻率上有干擾信號，也就是一個信道上有干擾。本次仿真采用正弦波發生器實現單頻干擾，通過改變其幅度和頻率的值，觀察其對跳頻系統的影響。仿真模型如圖9所示。

圖9 單頻干擾仿真模型

采用一個頻點為0.5 MHz的正弦波發生器模塊進行干擾。在信噪比為10 dB的情況下，不同信干比得到了不同的誤碼率。從圖10的仿真結果可以看到，單頻干擾對跳頻系統的干擾影響較小，誤碼率較小。當信干比越大時，誤碼率趨于不變，總小于10-1。所以，單干擾不能對跳頻系統造成有效干擾。理論上，單頻干擾只影響信號的很少一部分，也就是在干擾頻率上被干擾，而其他頻率不受影響。所以，通過仿真得到的結果與理論分析的單干擾對跳頻系統不起作用的結論基本吻合，說明跳頻系統對單頻干擾具有良好的抗干擾性能。

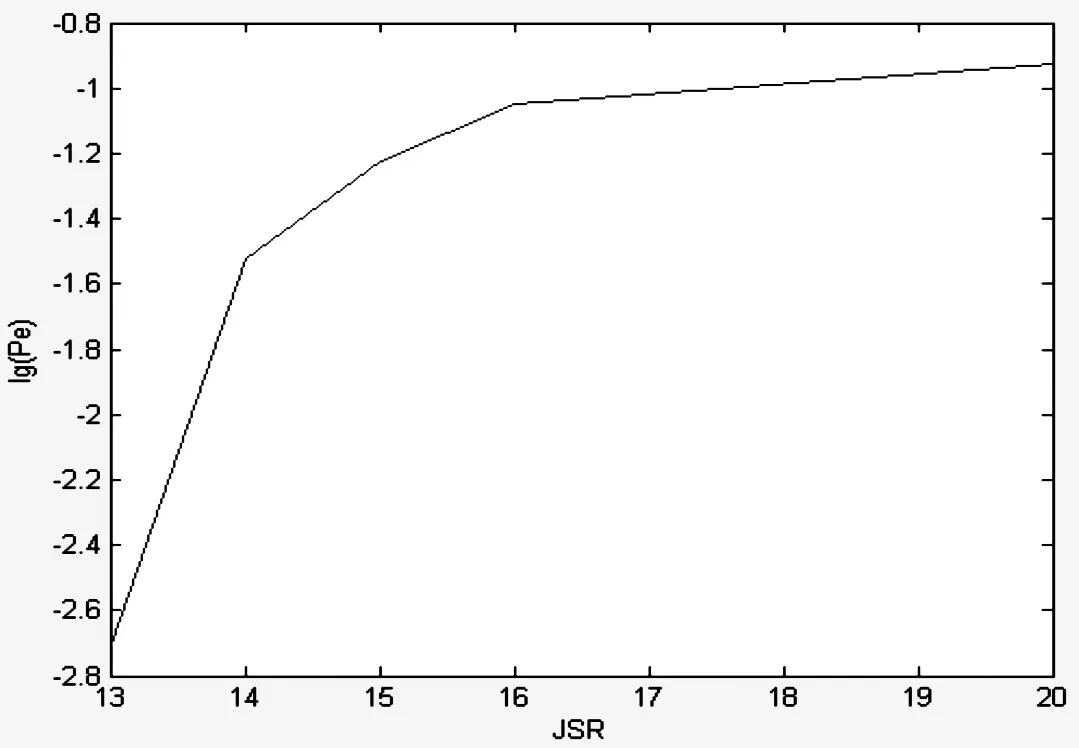
圖10 單頻干擾下BFSK跳頻誤碼率仿真曲線

3.3 多頻干擾

多頻干擾是在多個頻率上干擾，而不再是單個頻率干擾，其干擾時的功率更大。仿真時采用多個正弦波發生器相加來實現，設置正弦波發生器的不同頻率和不同幅度受到不同的干擾，其對跳頻系統的影響亦不同，仿真模型如圖11所示。

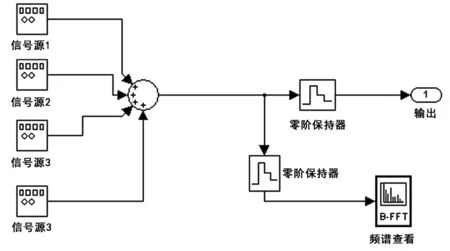
圖11 多頻干擾仿真模型

圖11中，4個正弦波發生器信號疊加，設置4個發生器的頻率分別為0.1 MHz、0.3 MHz、0.5 MHz和0.7 MHz，即可產生4個頻率的信號。將這4個信號疊加后的信號進行頻譜仿真，得到如圖12所示的頻譜圖。4個頻點均勻分布在跳頻系統的頻帶內，如果功率較大，對系統的干擾也會較大。

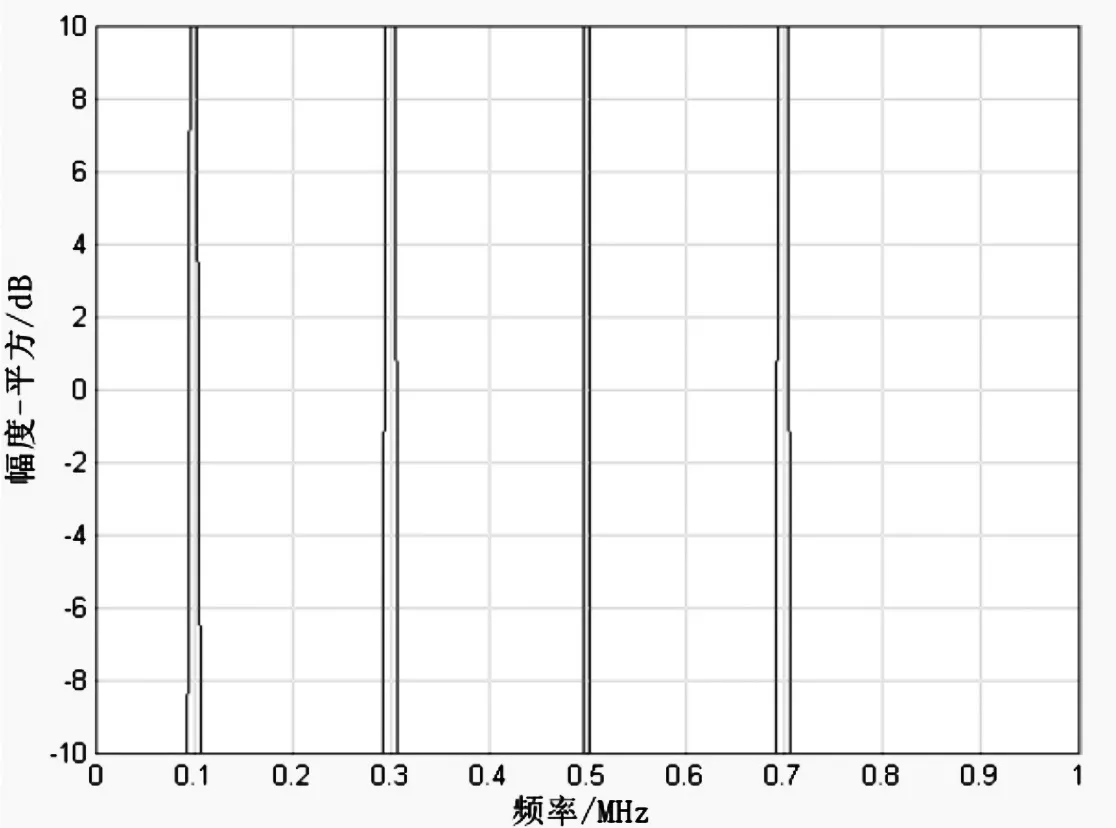
圖12 多頻干擾頻譜

圖13為多頻干擾在不同干信比時誤碼率的結果。橫軸為干信比，縱軸為誤碼率。改變干信比得到不同的誤碼率，可以看到，當干信比大于5 dB時，誤碼率Pe≥10-1，此時系統受到了較大干擾。當干信比為20 dB時，誤碼率很大，即使在干信比為0 dB時，誤碼率也能達到了2×10-2，可見多頻干擾對跳頻系統造成了較大影響。

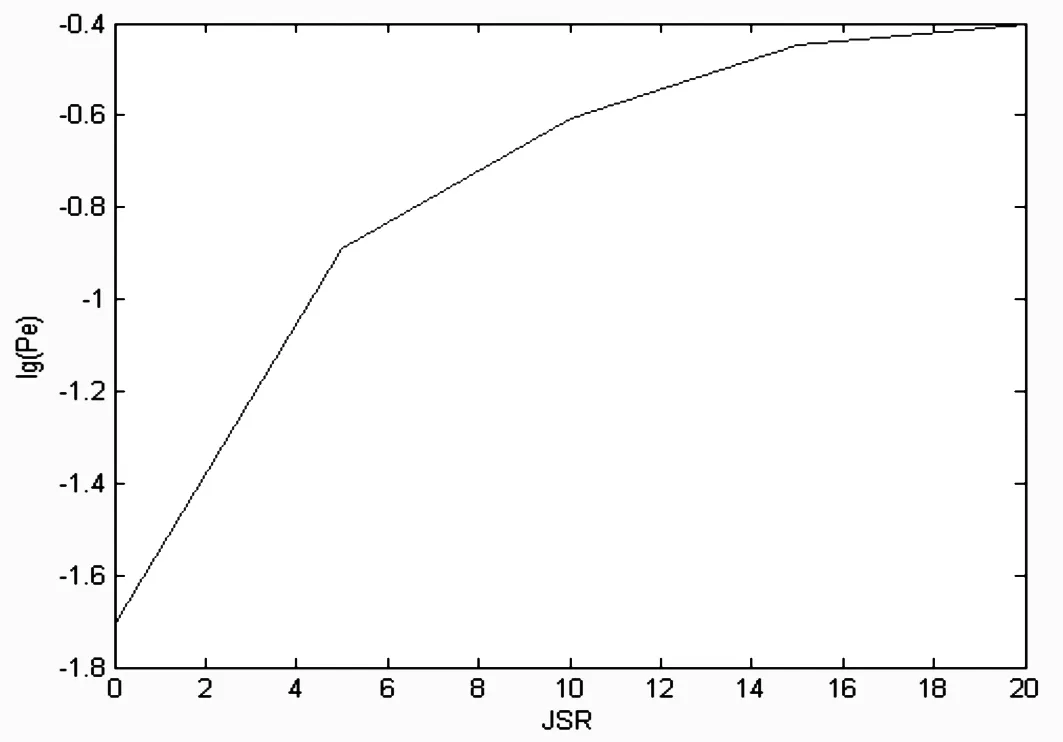
圖13 多頻干擾下BFSK跳頻誤碼率仿真曲線

4 結 語

跳頻通信是擴頻通信的一種，用多個載頻乘以原信號，而每個載頻由偽隨機碼控制。載頻的頻率變高，用載頻與原信號相乘，頻譜被擴展，就能躲避一定的干擾[3]。

從上述3種典型干擾對跳頻通信的影響可以看出，跳頻系統對抗定頻干擾有較好的性能。跳頻系統按照跳頻圖案跳變，但定頻干擾只有一個頻率，對通信干擾小，接收方也能正確恢復出信息。如果干擾有幾個頻率，跳頻系統的頻道數很大，則對系統性能的影響不大。

一般來說，跳頻帶寬越寬，跳頻的頻率數目越多，跳頻的速率越快，跳頻系統的抗干擾能力越強。

當然，一個跳頻系統的各項技術指標應當根據使用的要求、性能價格比等方面進行綜合考量，從而做出最佳的選擇。

[1] 高寶華,張濤.跳頻通信系統仿真[J].現代電子技術,2012(03):22-25.GAO Bao-hua,ZHANG Tao.Frequency Hopping Communication System Simulation[J].Modern Electronic Technology,2012(03):22-25.

[2] 王晨光,王振華.跳頻通信干擾裝備干擾效能分析[J].空軍雷達學院學報,2012(02):21-22.WANG Chen-guang,WANG Zhen-hua.Interference Effectiveness Analysis of Frequency Hopping Communication Jamming Equipment[J].Journal of Air Force Radar,2012(02):21-22.

[3] 樊昌信,曹麗娜.通信原理[M].北京:國防工業出版社,2014：399-400.FAN Chang-xin,CAO Li-na.Communication Principle[M].Beijing:National Defense Industry Press,2014:399-400.