基于人工蜂群算法的無人機協同路徑規劃

夏 瑞，趙 磊，吳書宇，李 軍

（四川大學 電子信息學院，四川 成都 610200）

在當今世界，隨著智能化自主化研究的不斷深入，無人機作為航空領域的標志性成果之一，得到了更加廣泛深入的研究，而關于無人機的可行性路徑的規劃更是一大研究熱門，對路徑規劃的研究始于20世紀60年代，國內外學者提出了大量的路徑規劃算法，包括A*算法、Voronoi圖算法引、動態規劃方法、仿生學算法等[1]。

由于路徑規劃問題具有高時間復雜度，所以問題的求解時間會隨著問題的規模呈指數型增長，尤其在復雜環境或者搜索空間比較大的情況下，上述所有算法的計算成本會急劇增加。由此，本文提出了一種新的基于人工蜂群算法（Artificial Bee Colony，ABC）的非確定性和雙向搜索機制結合的規劃算法，用于無人機路徑規劃。

人工蜂群算法由土耳其學者Karaboga[2]于2005年提出，是通過模擬蜜蜂群體尋找優良蜜源的行為方式解決實際工程優化問題的仿生智能計算方法，由于其在優化方面的高效性能，人工蜂群算法自提出以來得到了眾多學者的極大關注，隨著研究的不斷深入，人工蜂群算法得到不斷的改進，應用的領域也越來越廣。

同時，本文綜合考慮多無人機群的任務和任務區域的特點，合理構建了多UAV機群執行任務的問題模型，將以上提到的方法應用于多無人機群的路徑規劃問題的研究中，初步實現多無人機的協同規劃的兩種模型[3]。

1 無人機路徑規劃

1.1 環境模型及規劃空間的建立

1.1.1 針對小型無人機的三維環境建模

對于小型無人機，其面對的飛行環境實際情況比較復雜，且無人機受到其機動能力的限制，因此，如何保證規劃出的航路安全可飛是此類情況需首要解決問題。文獻[4]提出了一種綜合平滑算法，通過對地形坡度和曲率進行限制和平滑處理，使無人機在各個方向上的離地距離在安全范圍內。采用這種綜合地形平滑算法，可以得到綜合等效地形曲面z(x, y)，如圖1所示，在此基礎上，計算最小安全離地高度h[5]，并與曲面z(x, y) 相疊加，可得到一個新的安全飛行曲面H(x, y )。該曲面可表述為：

本文將在所形成的安全飛行曲面上，通過人工蜂群算法對其進行限制搜索，即可在安全曲面上得到三維航路，保證了飛行的安全性。

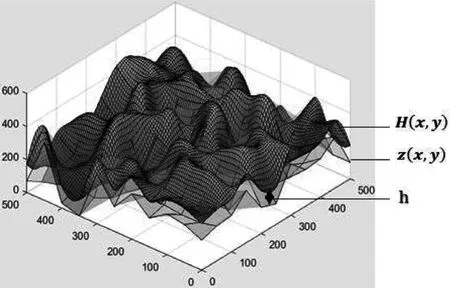
圖1 綜合等效地形

1.1.2 針對體型較大無人機的三維環境建模

對于較大型的無人機，其飛行航路雖然是三維的，但在實際情況中，可以考慮其是在定高飛行時的航路規劃，在二維空間內搜索航路。文獻[6]給出如下方法。

一般的地形可分為平原、山地以及高原等，為了模擬各類地形，可采取簡化的方法來構建環境模型。以山地地形為例，單個山峰個地形可由如下公式模擬：

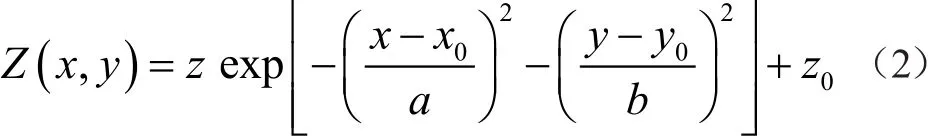
公式中，Z(x,y)表示山峰地形的高度，z為基準地形高度z0上山峰的高度；x0、y0是山峰中心O的坐標；在一定高度H上取山地截面，可得到一橢圓形。該橢圓形長軸長為a，短軸長為b，a，b值越大，則山峰越平坦，反之則越陡峭，如圖2所示。

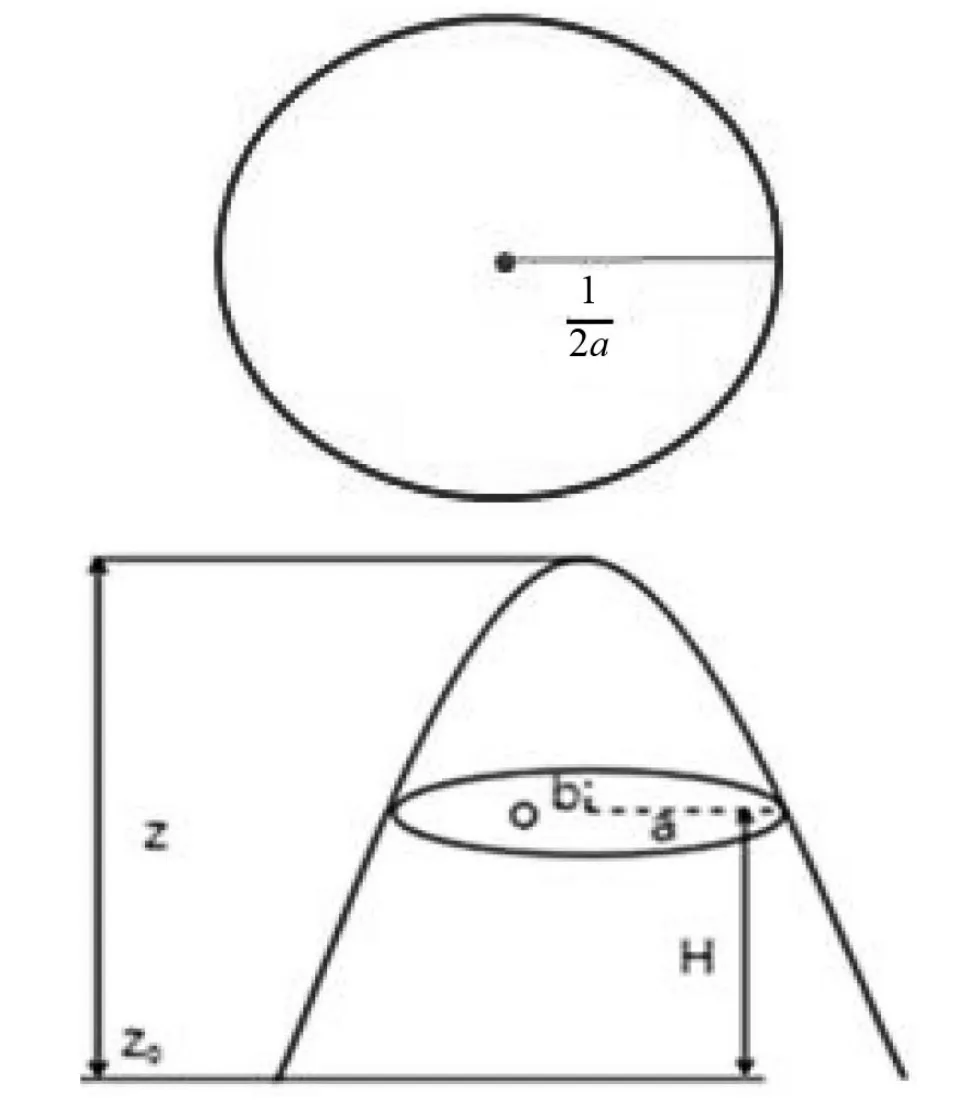
圖2 山峰威脅示意

因此，可以將山峰威脅定高H二維平面時，威脅模型可表示為(x，y，max(a，b))，max(a，b)為取a，b中的最大者。該區域為無人機不可飛區域，無人機一旦進入該區域則會墜毀，即在該區域內無人機損壞概率為1。該區域用如下集合表述：

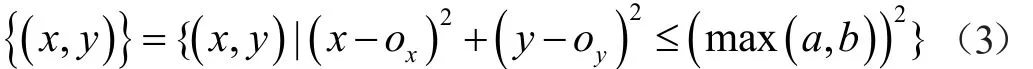
因此，將地形威脅信息表示為(x，y，max(a，b))。

我們選取截取后得到的橢圓形，以長軸為直徑，O為圓心畫圓，可得出地形的近似模擬。經過Matlab模擬可得如圖3所示的環境模型。

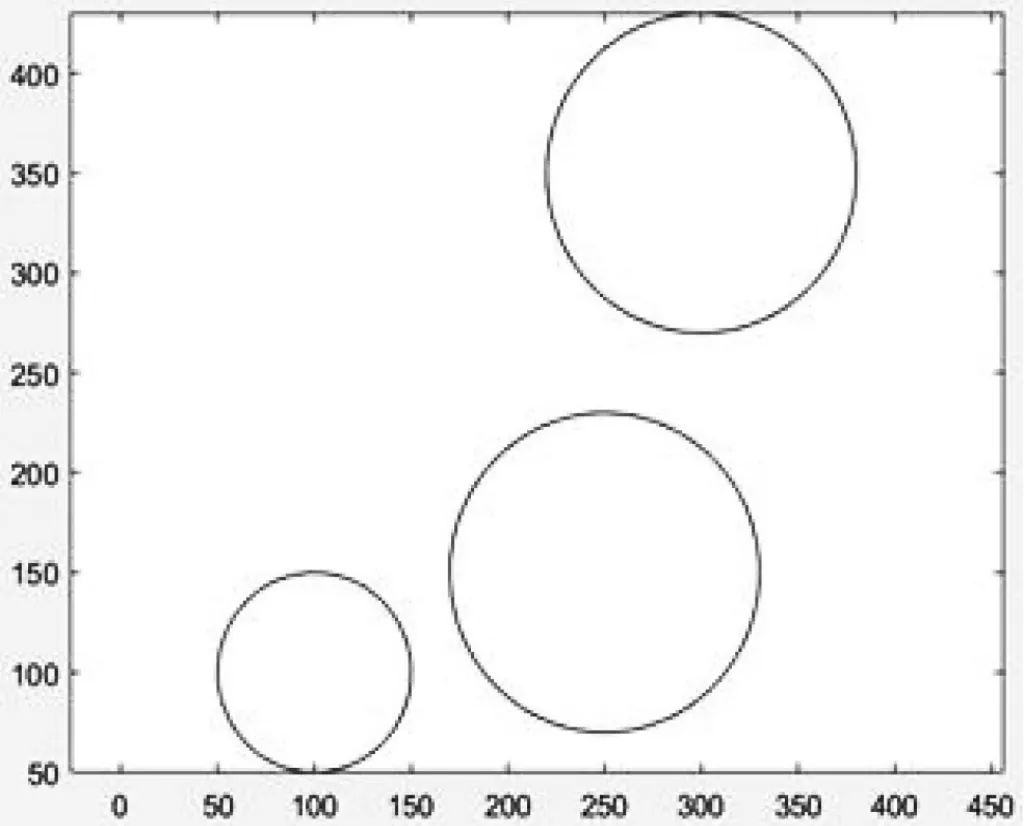
圖3 Matlab仿真地形示意

1.1.3 威脅區域的量化

有效地躲避防空威脅是無人機路徑規劃的主要目的之一。在對無人機進行航路規劃之前，需要對威脅建模并轉化為規劃算法能夠使用的量化信息。如果依據每種防空武器的特性精確建立各種威脅模型，分析起來極其復雜。本文采用簡化模型的方法，如Menon等[7]提出了最小威脅曲面的概念，該方法主要根據威脅作用強度和作用半徑將其等效為特殊山體，然后疊加到數字地圖上的相應位置，得到綜合威脅和地形地物的等效數字地圖（見圖4），從而將威脅回避轉化為地形回避來處理。

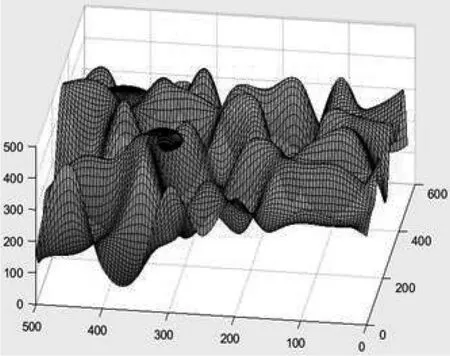
圖4 威脅區域與地形疊加示意

1.2 單無人機路徑規劃

1.2.1 單無人機路徑規劃問題描述

單無人機的路徑規劃需要模擬出外界地形環境條件參數和飛行過程中的可能威脅區域，綜合考慮無人機自身的性能，如無人機的飛行高度、轉角度數、飛行距離等，規劃出一條從起點到終點的滿足各方面要求的合理路線。

1.2.2 約束條件

實際無人機路徑規劃有很多約束條件，比如飛行途中的障礙物及可能發生危險的區域、無人機自身性能的限制，使得路徑規劃必須在這些約束下進行。通常考慮的約束條件有：最小飛行長度、最大飛行距離、飛行轉彎夾角、威脅區域。

（1）最小飛行長度。

鑒于無人機在改變飛行狀態之后持續直線飛行有著最小長度l min的限制，需約束最小飛行長度，即算法中路徑規劃任意兩相鄰節點之間的距離Li應滿足：

（2）最大飛行距離。

由于考慮無人機能夠攜帶的燃料有限，無人機的飛行總路徑需要受到一定的限制，可分為以下兩種情形。

①如果沒有設定最大飛行距離，路徑規劃就以尋找到最短路徑為目的，盡可能規劃出可行的總長短的路徑。

②設定了最大飛行距離Lmax，則對于路徑總長度應該滿足：

（3）飛行轉彎夾角。

無人機在飛行轉彎過程中有著對轉彎角度的要求，如果轉彎角度過小無人機則無法完成轉彎動作，因此在對路徑選擇的時候需要規定轉角范圍。

如圖5所示，設已完成的點N1，N2，接下來需要確定的路徑節點N3，本路徑采用余弦公式利用向量計算得到N1N2，N2N3兩段路徑的夾角的余弦值：

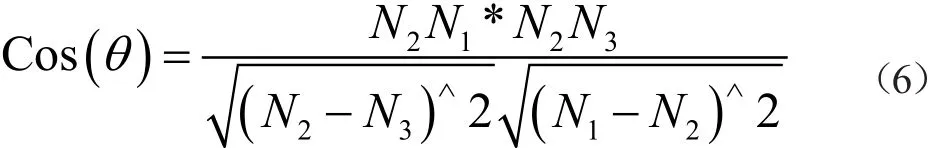
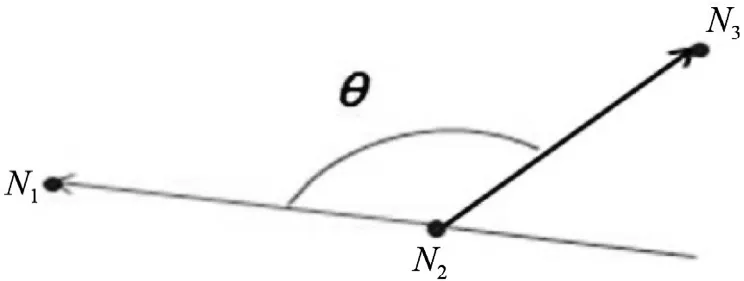
圖5 飛行轉彎夾角示意

若設定θ為鈍角時滿足無人機飛行轉彎性能限制，則轉換為滿足條件：

（4）威脅區域。

威脅區域即無人機飛行途中遇見的如有導彈打擊、雷雨等不便通過的區域，在實際情形中無人機可能有0～1的概率不可飛過威脅區域，為了使情況簡單，本路徑一律使用威脅區域的威脅因素為1，即不可進入威脅區域，處理原理與不完全概率一致。

對于一個以中心點為圓心，半徑為R的威脅區域，無人機路徑需要避開，要求路徑節點在此區域之外，如圖6所示，即滿足：

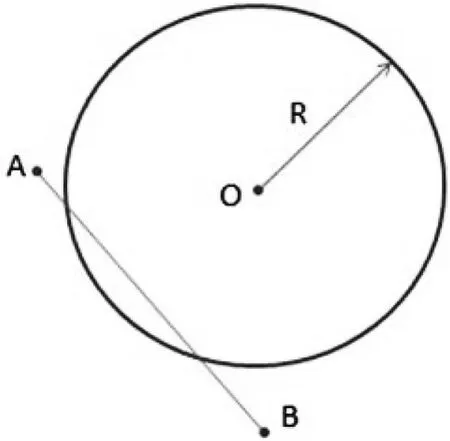
圖6 威脅區域

其中可能存在兩節點不在威脅區域內，但是連接起來之后的路徑有部分在威脅區域內，則可以使用增加節點數量的方法使路徑全部置于威脅區域之外，如圖7所示。

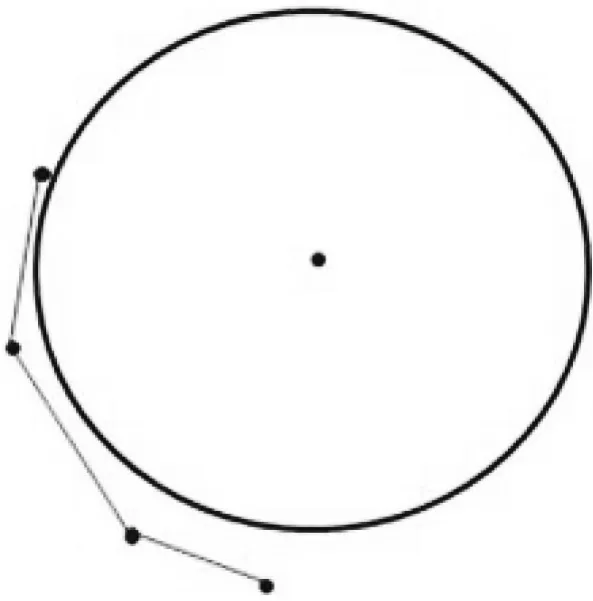
圖7 威脅區域特例

本文采用ABC算法對路徑規劃問題進行求解，則需要建立合適的代價函數。為此，本文將所有約束條件通過公式（9）統一起來，產生一個總的代價函數。fk為各約束條件表達式，Weightk表示不同的約束條件所占權重大小，通過在仿真過程中不斷改變權重比例關系能得到產生較好路徑的最佳權重比。

求解最優解點就變成了求解該代價函數最小值是對應的各坐標參數。

1.2.3 航跡規劃算法步驟

（1）初始化算法及其參數，主要設定的參數有起點setstartj、終點setfinalj、威脅區域相關信息（威脅坐標及威脅區域半徑）、路徑夾角與長度所占權重Weightk、算法迭代次數MaxCycle、算法運行次數2*runtime、蜜蜂總數NP、食物總數NP/2、環境上下限(xmax,xmin)、環境維度D、蜜源未更新次數上限NP*D（limit）、路徑節點數node、初始化路徑節點數組GlobalParamsmj={setstartj;0; setfinalj}，j={1、2、3}，為D維解向量的某個分量，m={1、2、3……node}。

其中，對于路徑節點數的確定本文采用動態選取的方式，即對于不同長度的路徑確定不同數量的節點數使節點大致呈均勻分布，通過對起點終點直接連線求得路徑直線長度L，反復調試設定不同的兩相鄰節點之間長度Lfen，最終得出最合適的節點間距Lfen，且runtime=node+1。

（2）改進ABC算法中初始蜜源（節點）的產生方式，在原有公式（11）的基礎上，再通過公式（12）、（13）增加維度限制條件，簡化搜索范圍，同時使所產生的節點均勻化分布。

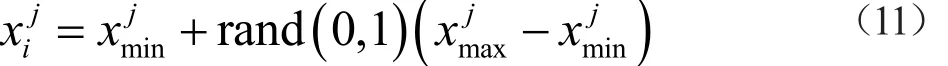
式中：i={1、2、3……NP/2}，為蜜源（可行解）編號。

iter為與MaxCycle做比較的計數器。

（3）根據代價函數函數計算公式（9）計算每個可行解的總代價值，再通過公式（14）計算其適宜度。

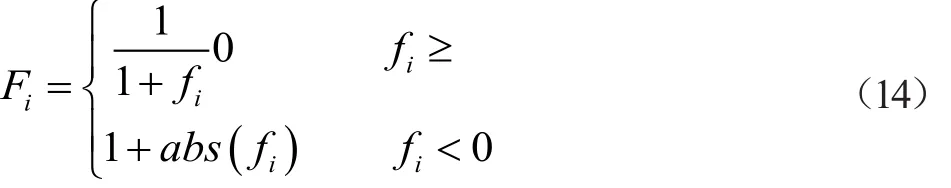
（4）根據公式（15）進行開采，尋找新節點。

其中：xk代表領域蜜源，k取值于{1,2,…NP/2}，且k不等于1，φij是取值在[-1,1]內的隨機數，通過式（15）得到新蜜源后，利用貪婪算法，比較新舊蜜源適應度，選擇優者。

（5）跟隨蜂通過公式（16），用輪盤賭方式進行貪婪選擇蜜源，通過公式（15）進行進一步開采。

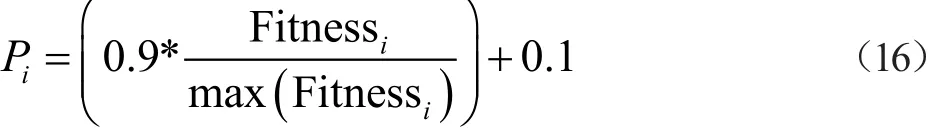
蜜源擁有參數trial，當蜜源更新被保留時，trail為0，反之，trail加1。從而trial能統計出一個蜜源沒有被更新的次數，用于limit的比較。

（6）如果一個蜜源經過多次開采沒被更新，也就是trial值過高，超過了預定閾值limit，那么需拋棄這個蜜源，啟動探索峰階段。這體現了ABC里自組織的負反饋和波動屬性[8]。在該階段里，探索蜂利用步驟（2）中的公式隨機尋找新的蜜源來代替被拋棄蜜源。

（7）迭代次數iter加一，重復（3）～（6）過程，得到更優適應度的節點，直至迭代次數達到MaxCycle，運行次數r+1。

（8）繼續執行第（3）～（7）步，求解下一個節點，直至規劃完node個節點。

（9）路徑節點優化，增加步驟（2）中的維度限制條件

（10）對產生的節點進行B樣條平滑處理，繪制規劃效果，輸出相應規劃結果。

1.2.4 算法規劃特點

（1）采取智能算法解決無人機路徑規劃問題。

將人工蜂群算法結合無人機路徑規劃這一特定問題，對算法進行相應改造，以適用于這一特定問題的解。基于ABC算法的路徑規劃問題對應關系如表1所示。

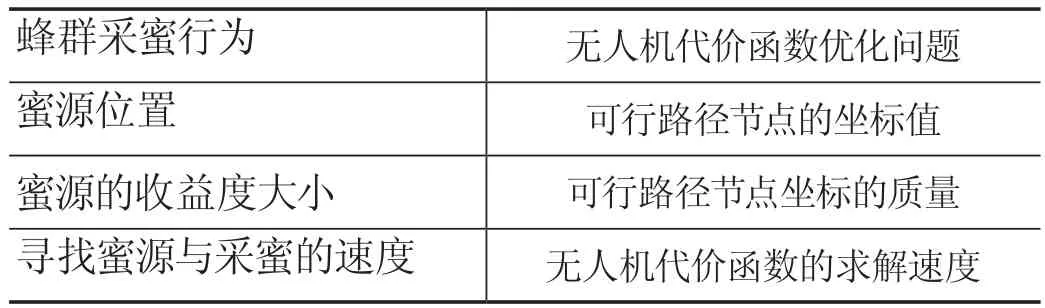
表1 基于ABC算法的路徑規劃問題對應關系

（2）采用非確定性規劃方法。

由于確定性規劃方法存在一定的缺陷，我們采用隨機搜索方法搜索航路。所謂確定性規劃，即任意兩個點之間的可選路徑條數是可數的，而在非確定性規劃中是無窮多的，與之特點對應的，其規劃出來的路徑具有更高的精確性。確定性規劃方法和非確定性規劃方法示意如圖8—9所示。

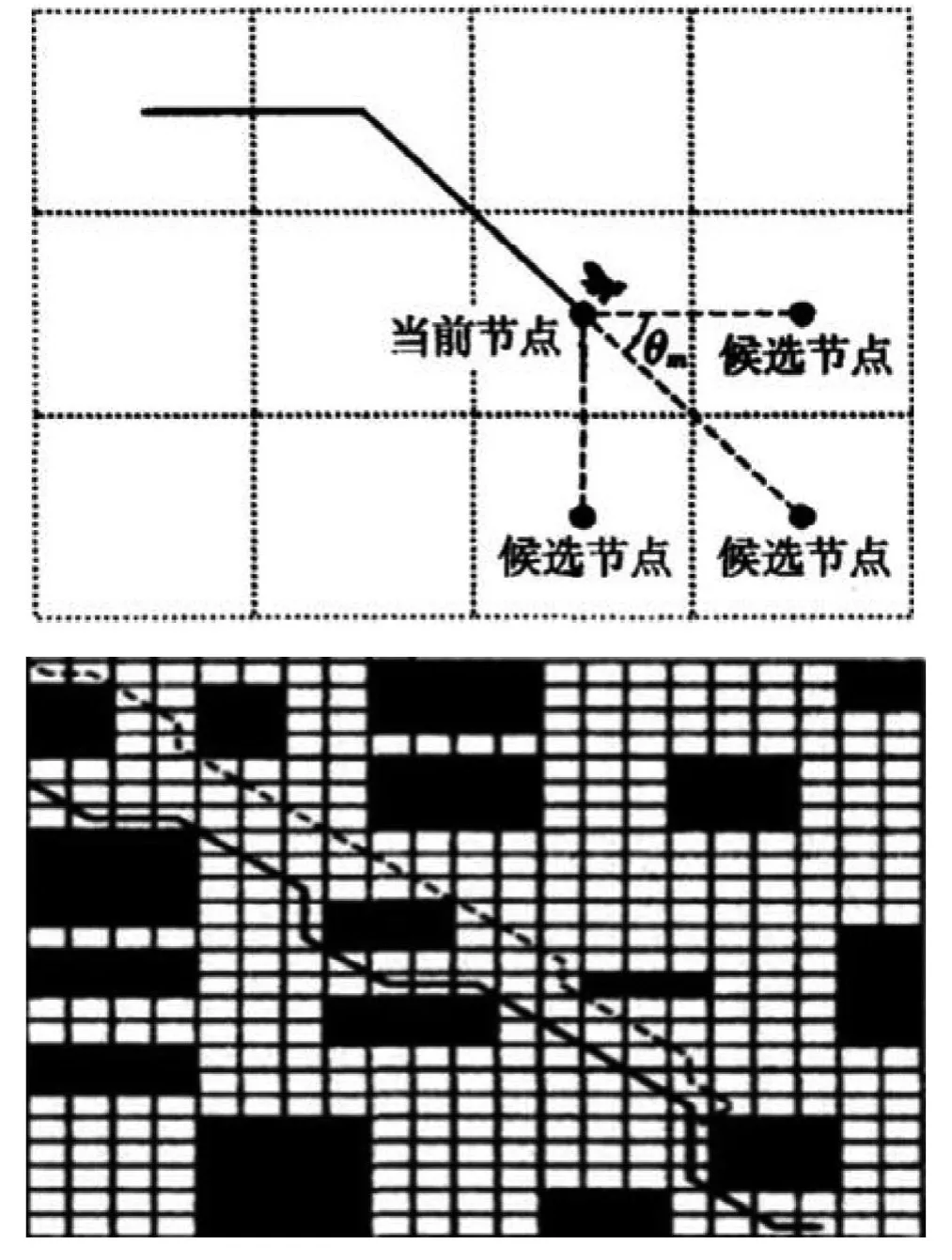
圖8 確定性規劃方法示意

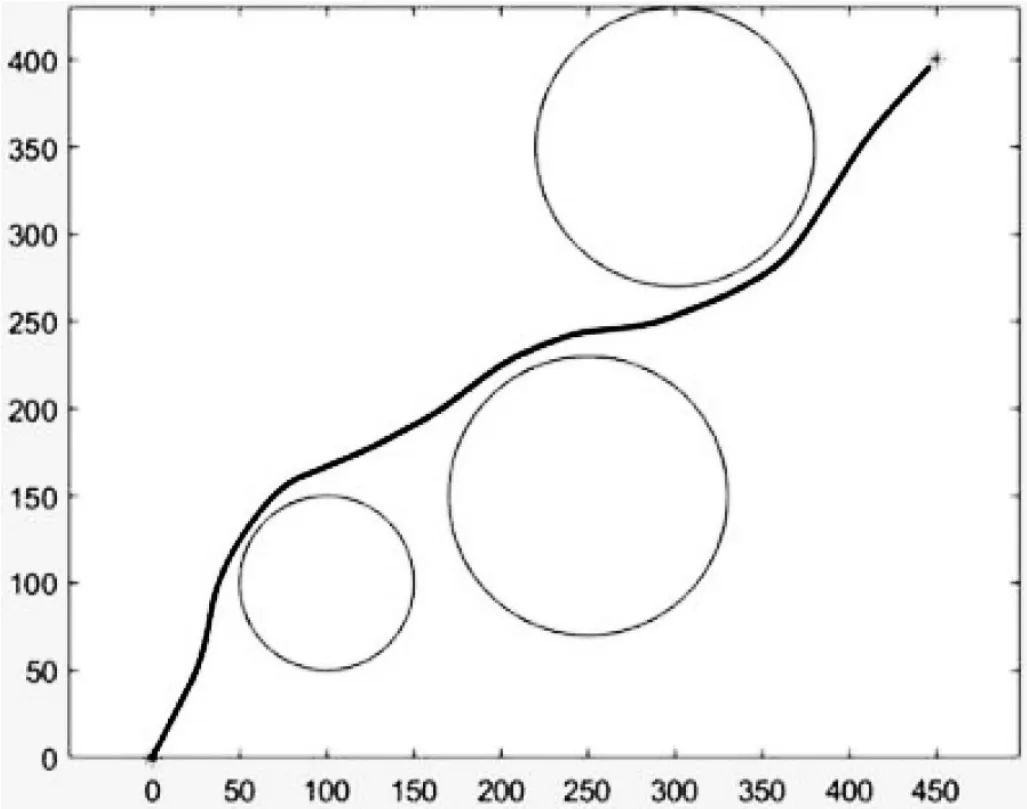
圖9 非確定性規劃方法示意

在隨機方法中我們將路徑規劃這一大問題分解為路徑中重要節點的規劃問題上，采用此方法有以下優點：①可以通過調整航路節點的數目達到任意的精度。②將原始的規劃問題分解為一組統一的規模較小的子問題。在每個子問題中，關心的僅僅是一個點的坐標。考察航路是否可行，是否滿足約束條件變為僅考察一個點或者一條線段是否滿足要求。③由于將航路規劃問題局限為一系列航路節點，從而便于實現大量的并行/分布式計算，這與人工蜂群算法的特點很好融合。

（3）采用基于雙向規劃機制[1]的節點確定方法進行路徑規劃算法設計。

在傳統路徑規劃算法中，一條路徑的生成通常是從起點開始，到終點結束，不能充分發揮蜂群群體協作的特性，因此影響了算法的效率和收斂速度，而且不能很好滿足任務的環境約束，基于雙向搜索機制的路徑節點確定方法能夠有效解決這個問題。流程如圖10所示。

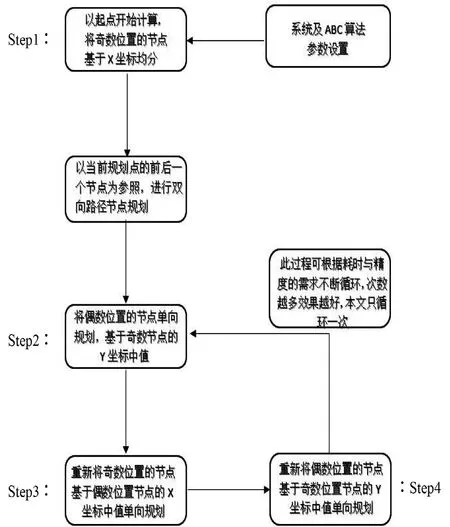
圖10 雙向規劃節點確定流程

方法具體步驟如下。

Step1：以起點開始，規劃奇數位置的節點。根據起始兩點距離，大致均勻化固定節點的橫坐標值，使規劃問題降維，即將這一個點的規劃空間固定到以橫坐標為定值的一平面（三維環境下）或一直線（二維環境下），將蜂群尋優過程進行間隔分塊，進行雙向路徑節點規劃，即按照（1，node，3，node－2···(node+1)/2）的順序規劃，尋找到滿足使代價函數值最小的點。其中node為路徑節點個數，且為奇數。

Step2：利用Step1中所產生節點，同樣采用降維思想，固定偶數位置節點的縱坐標值。按照（2，4，6，···node－1）的順序規劃，尋找到滿足使代價函數值最小的點。

Step3：采用同樣的方法，固定奇數位置節點的橫坐標值，再次對奇數位置的節點進行規劃。

Step4：采用同樣的方法，固定偶數位置節點的縱坐標值，再次對偶數位置的節點進行規劃。

根據理論分析，此方法的Step2～Step4可以一直循環進行，每循環一次，效果便會好一些，但是時間代價會成倍增加。

1.2.5 B樣條路徑平滑算法

B樣條（De Boor）[9]在數學的子學科數值分析里是樣條曲線一種特殊的表示形式，由Isaac Jacob Schoenberg創造的，是基（basis）樣條的縮略。B樣條方法具有表示與設計自由型曲線曲面的強大功能，是形狀數學描述的主流方法之一，另外B樣條方法是目前工業產品幾何定義國際標準—有理B樣條方法（NURBS）的基礎。B樣條方法兼備了Bezier方法的一切優點，包括幾何不變性、仿射不變性等，同時克服了Bezier方法中由于整體表示帶來不具有局部性質的缺點（移動一個控制頂點將會影響整個曲線）。B樣條曲線方程可寫為：

其中：di(i=0,1...n)為控制頂點（坐標），Ni,k(i=0,1...n)為k次規范B樣條基函數，最高次數是k。基函數是由一個稱為節點矢量的非遞減參數u的序列U：u0≤u1≤...≤un+k+1所決定的k次分段。

B樣條的基函數通常采用Cox-deBoor遞推公式：

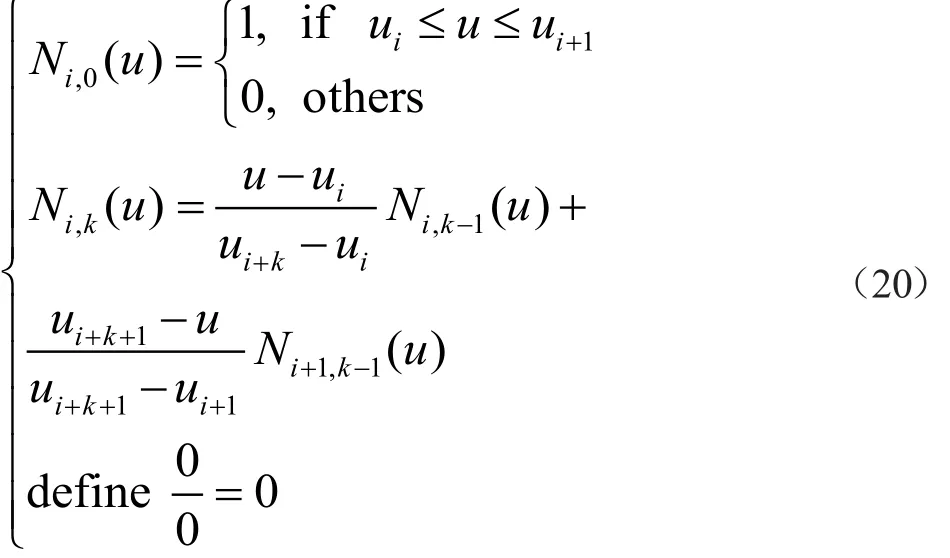
式中：i為節點序號，k是基函數的次數，共有n+1個控制頂點。注意區分節點和控制頂點，節點是在節點矢量U中取得，控制頂點則是坐標點，決定B樣條的控制多邊形。CoxdeBoor遞推公式是B樣條曲線的定義的核心，該部分在程序中實現可采用遞歸的方式。

常見的B樣條曲線有以下3種。

①均勻B樣條曲線：節點矢量中節點為沿參數軸均勻或等距分布，如圖11所示。

②準均勻B樣條曲線：其節點矢量中兩端節點具有重復度k+1，即u0=u1=...=uk，un+1=un+2=...=un+k+1，所有的內節點均勻分布，具有重復度1，如圖12所示。

③分段Bezier曲線：其節點矢量中兩端節點的重復度與類型2相同，為k+1。不同的是內節點重復度為k。該類型有限制條件，控制頂點數減1必須等于次數的正整數倍，即n/k=正整數，如圖13所示。

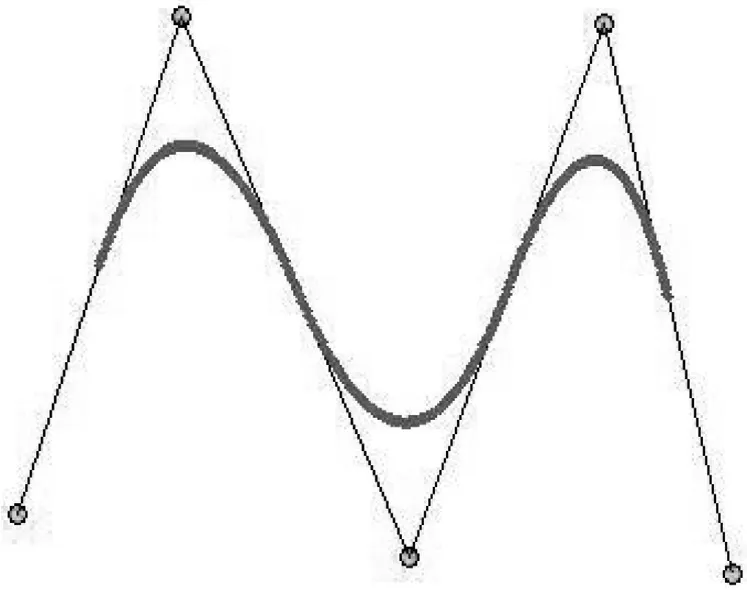
圖11 均勻B樣條曲線

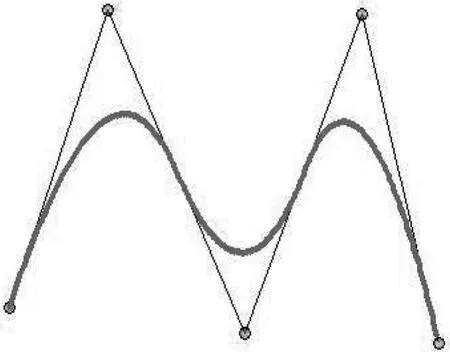
圖12 準均勻B樣條曲線

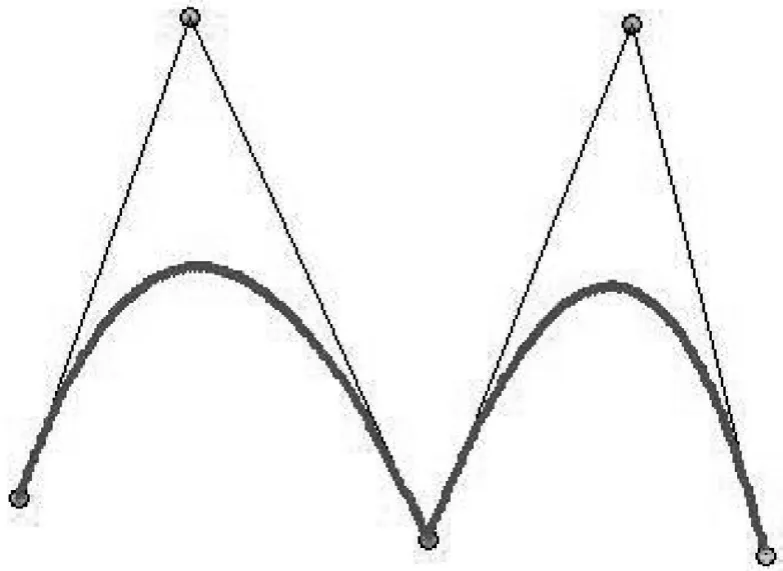
圖13 分段Bezier曲線

本文利用人工蜂群算法得出路徑散點之后，采用準均勻B樣條路徑平滑方法平滑散點，路徑規劃效果有了顯著的改變（見圖14—15）。產生交集。多無人機規劃路徑產生示意如圖16所示。

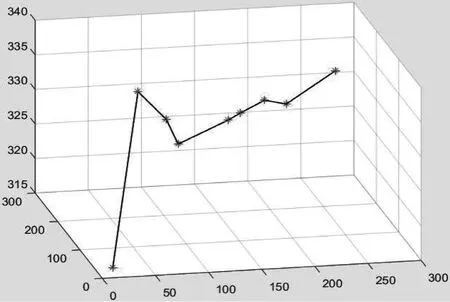
圖14 平滑之前

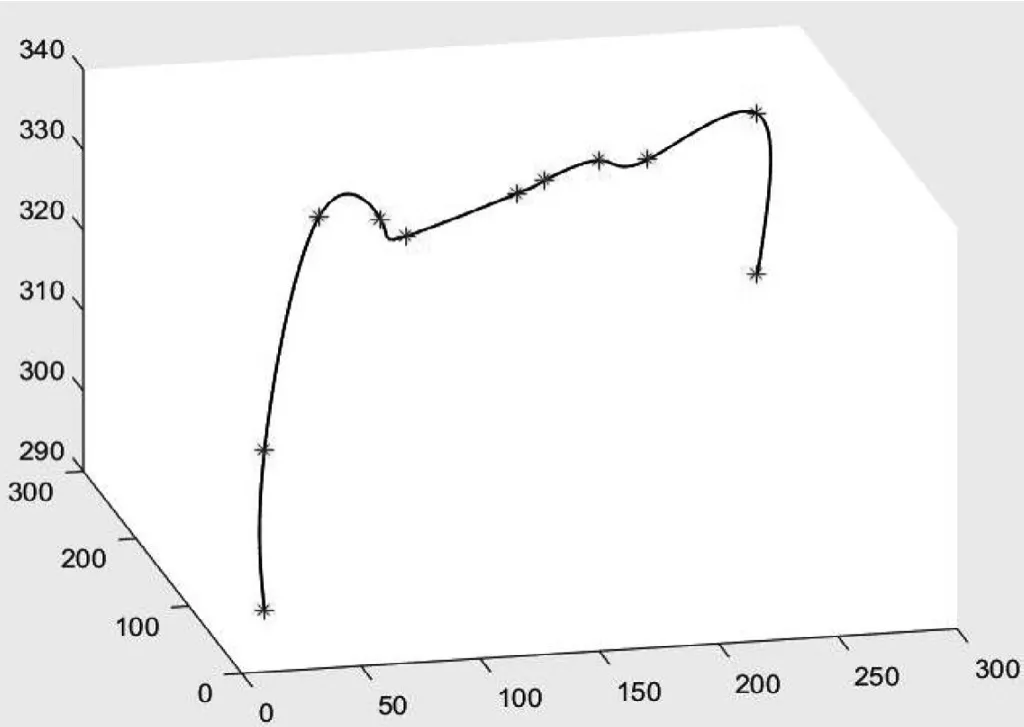
圖15 平滑之后

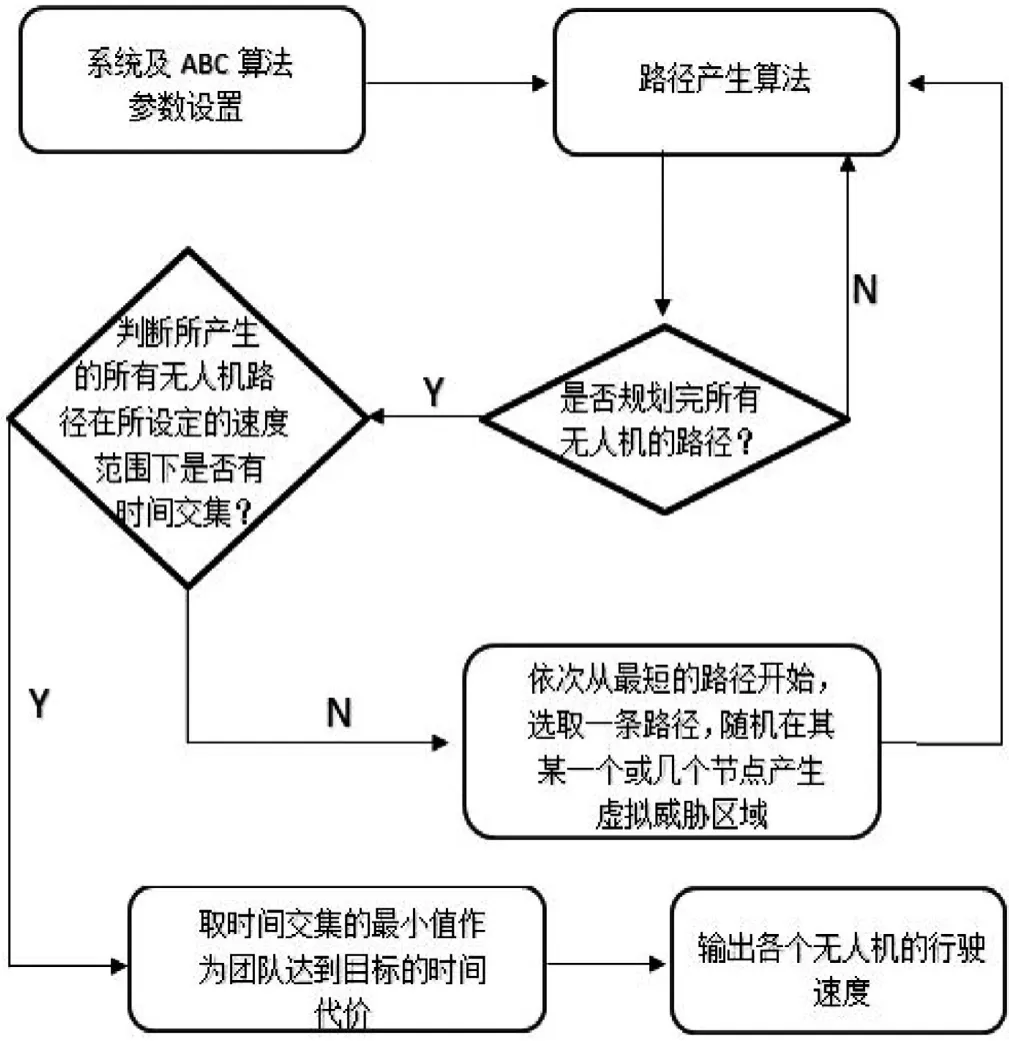
圖16 多無人機規劃路徑產生示意

1.3 多無人機路徑規劃

本文應用前面所提到的規劃算法，初步建立了兩個多無人機協同規劃的模型，并通過Matlab對其進行仿真實現。

（1）考慮多無人機不同起點，同一終點，同時起飛，同時到達。規劃時，系統根據文章前面提到的路徑產生算法，生成所有無人機路徑，并判斷所有無人機在所設定的速度范圍下是否有時間交集，若有，則取時間交集的最小值作為團隊達到目標的時間代價，并輸出各個無人機的飛行速度。若沒有，則依次對路徑最短的無人機根據公式（8）產生一個虛擬的威脅區域進行重新規劃，直到所有無人機的飛行時間

（2）考慮多無人機不同起點，同一終點，同時起飛，按照指定順序和時間間隔依次到達。規劃時，系統給每架無人機分別規劃路徑，計算所指定的第一架無人機以最大速度飛行的時間，對此后的無人機依次按照上一架無人機的飛行時間延時指定的時間間隔，然后依次對目前所規劃的時間進行越界判斷（即能否在此時間下通過自己的路徑），若能，則根據每架無人機的規劃時間計算出各自飛行速度，否則比較計數器和無人機的數量，若計數器小于無人機數，則以越界無人機通過其路徑的最快速度為基準，對其前后的無人機，依次按照上一架無人機的飛行時間延時指定的時間間隔，然后計數器加一，重復之前的判斷操作。若計數器數大于無人機數，則輸出錯誤，沒有規劃方案。特別的，當間隔時間為0的時候，可實現同時到達。多無人機規劃示意如圖17所示。

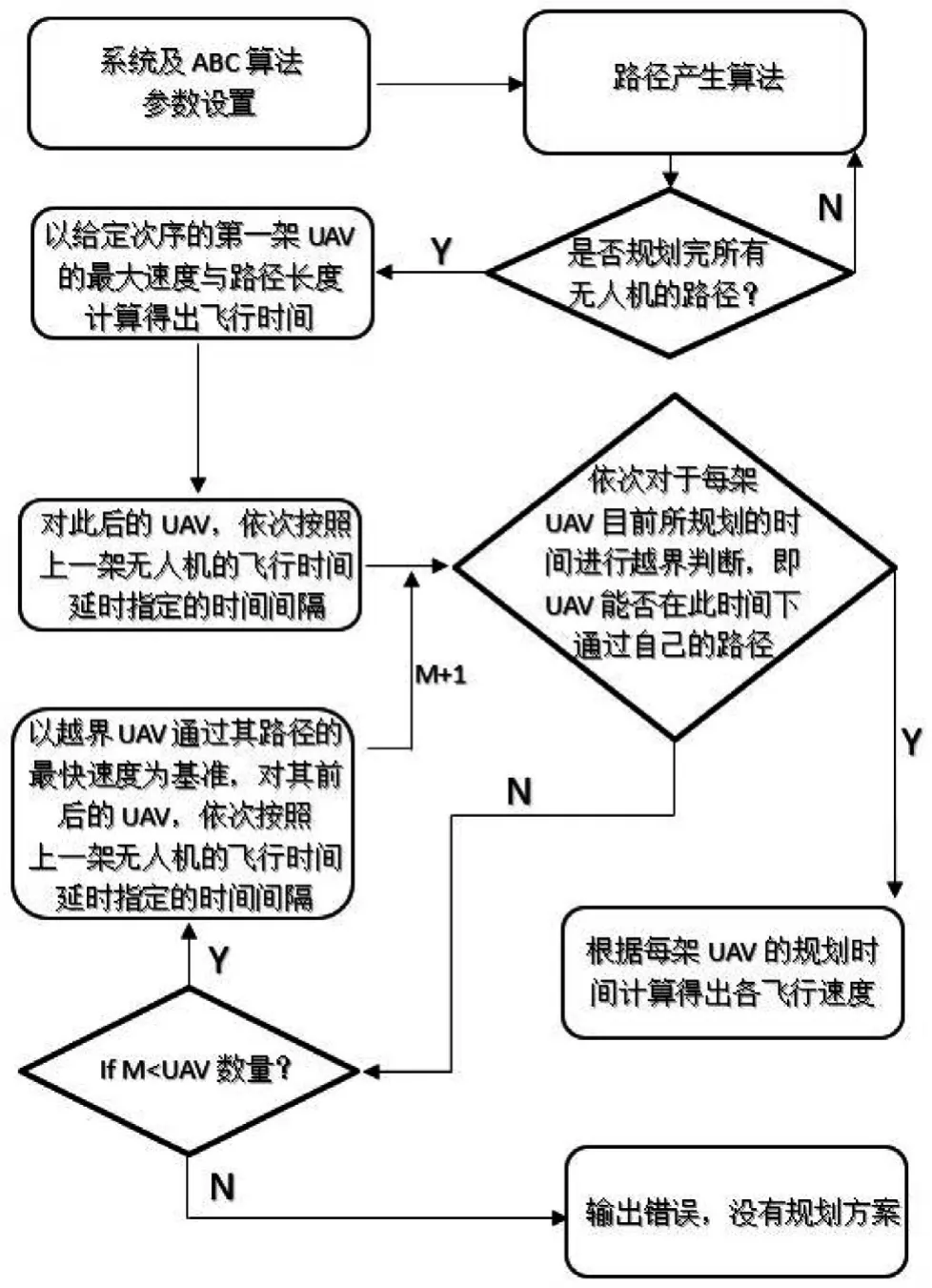
圖17 多無人機規劃示意

其中M為計數器，初始值為0。

2 仿真結果

采用上述航路規劃方法，利用Matlab R2016a對所設計的算法進行仿真。環境模型為威脅區域與障礙物的疊加，得到的航路均為經均勻化B樣條路徑法平滑后的航路。

2.1 單無人機規劃

（1）實驗1：在一塊500×500的數字地圖上進行仿真，仿真基本參數如下：無人機最小步長為30，飛行器的起點和目標點坐標分別為(0, 0)，(450, 400)，兩點直線距離為602.0797，最大航程約束為直線距離的1. 5倍。仿真實驗1所得結果如圖18所示。

得到路徑的長度為653.0710，規劃時間4.666 s。

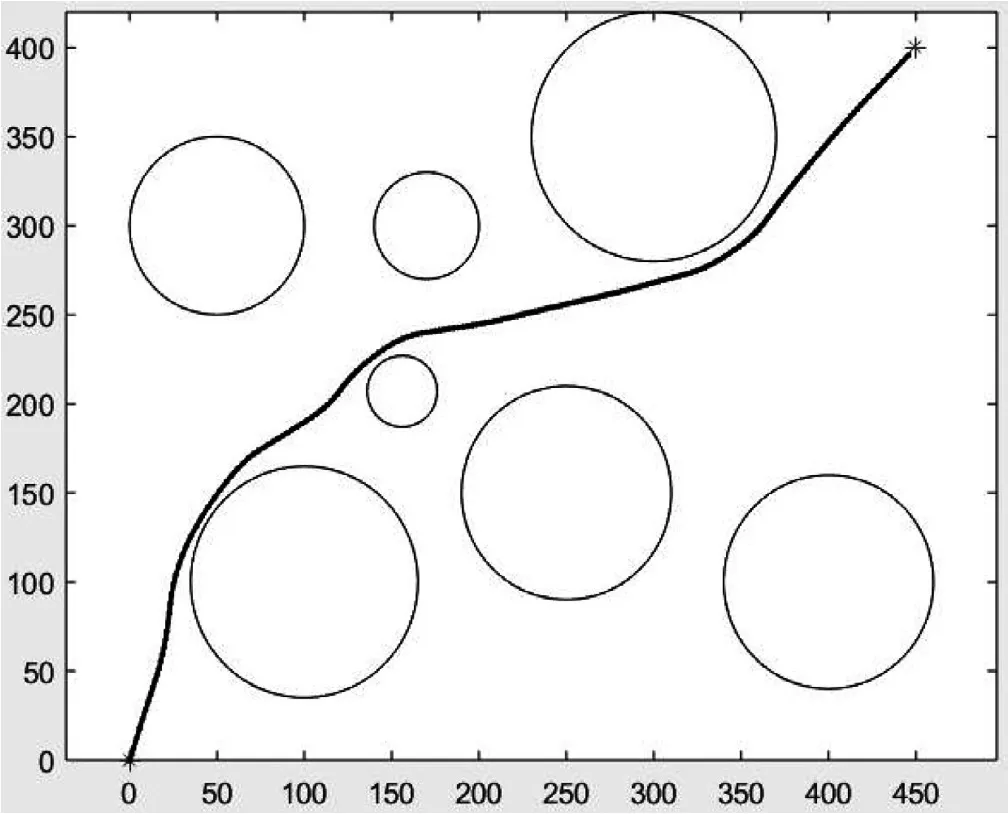
圖18 仿真實驗1所得結果

（2）實驗2：在一塊500×500×500的數字地圖上進行仿真，仿真基本參數如下：無人機最小步長為30，飛行器的起點和目標點坐標分別為（15.15, 30.3, 295.9），（449.5, 459.6,422），兩點直線距離為623.5861，最大航程約束為直線距離的1.5倍。仿真實驗2所得結果如圖19所示。

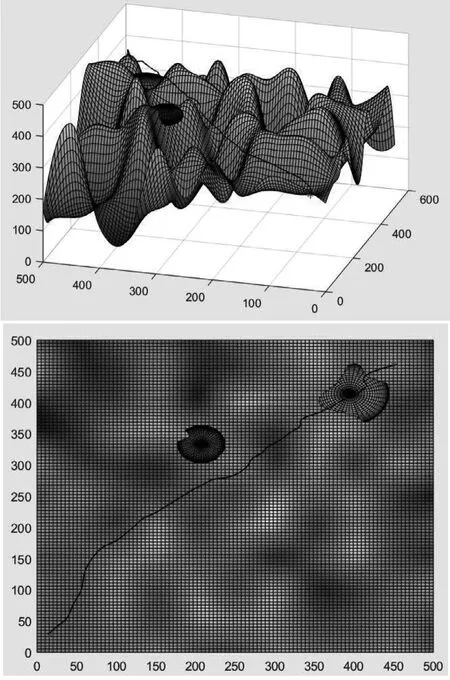
圖19 仿真實驗2所得結果

得到路徑的長度為661.6694，規劃時間22.240 s。

2.2 多無人機規劃

（1）實驗3：在一塊500×500的數字地圖上進行仿真，仿真基本參數如下：無人機最小步長為30，V∈(3,30)，飛行器的起點坐標分別為(0, 20)，(50, 450)，(500, 50)，(600, 600)，編號依次為1、2、3、4。設置無人機到達順序為{1，3，4，2}，時間間隔為5 s。仿真實驗3所得結果如圖20所示。多無人機規劃結果如表2所示。

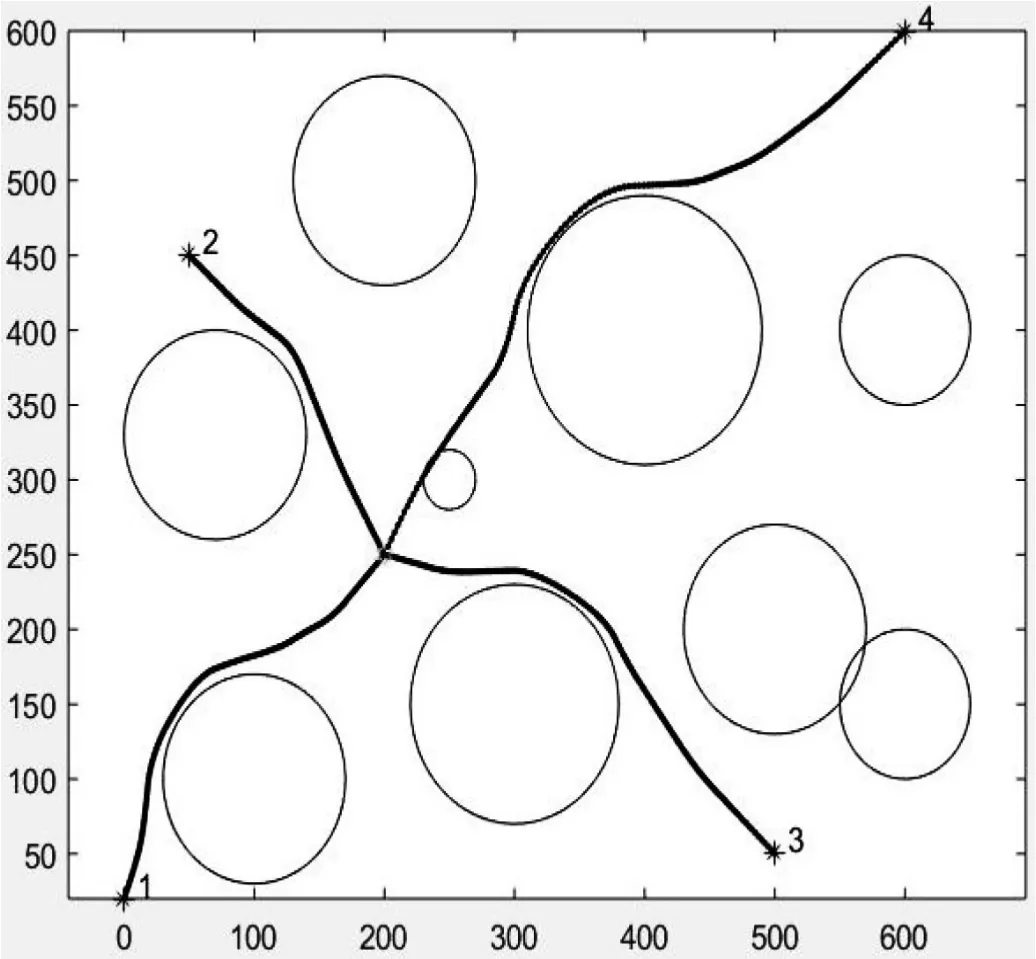
圖20 仿真實驗3所得結果

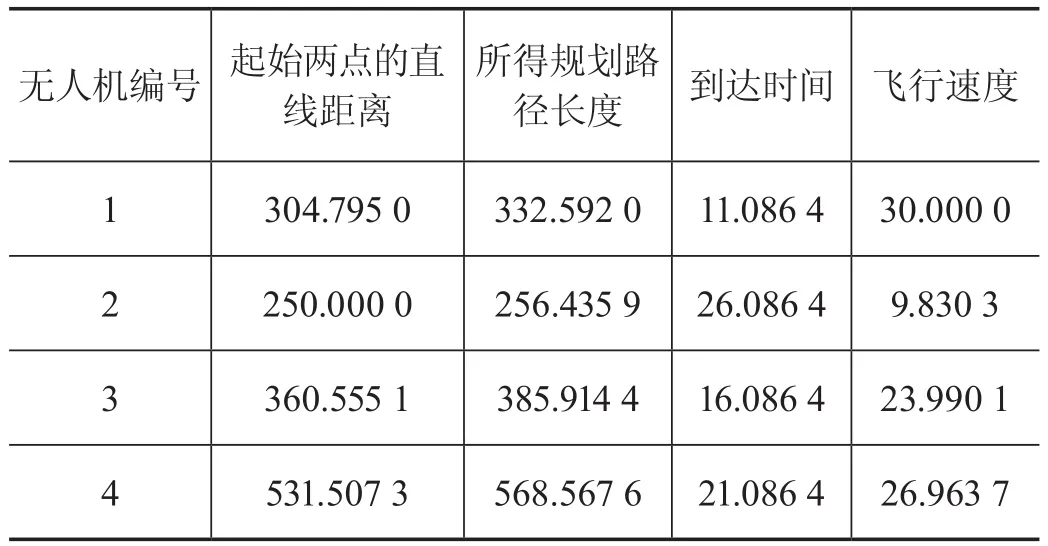
表2 實驗3多無人機規劃結果

所示結果符合預期，規劃時間為6.962 s。

（2）實驗4：在一塊500×500×500的數字地圖上進行仿真，仿真基本參數如下：無人機最小步長為30，V∈(3,30)，飛行器的起點坐標分別為(176.8, 237.4,254.5)，(161.6, 363.6, 429)，(454.5, 146.5, 228.2)，(393.9,308.1, 234.3)，編號依次為1、2、3、4。設置無人機到達順序為{1，4，2，3}，時間間隔為9 s。多無人機規劃結果如表3所示。

所示結果符合預期，規劃時間為32.912 s。

仿真結果表明，采用雙向規劃機制的非確定性節點規劃能很好地融入ABC算法，并能在較短時間內得到較好的路徑。

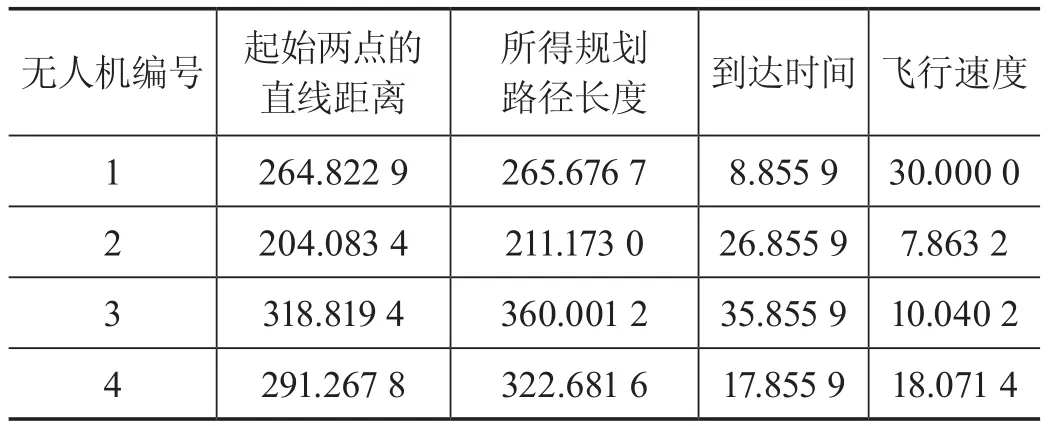
表3 實驗4多無人機規劃結果

圖21 仿真實驗4所得結果

3 結語

本文給出了一種基于改進人工蜂群算法的航路規劃方法實現。該方法將規劃空間的預處理和人工蜂群算法相結合，通過建立地形安全曲面和量化威脅信息，簡化規劃空間。在傳統人工蜂群算法的基礎上，改進了算法中食物產生的方式，將航跡規劃分解為各節點的規劃，并引入雙向規劃機制，大大提高了產生航跡的質量。同時應用我們給出的路徑規劃算法，對多無人機的兩種協同模型做出初步實現，仿真結果表明，算法可以快速規劃出滿足約束條件的三維航路，并能有效實現多無人機的初步協同，具有較強的工程可實現性。

[1]李喜剛，蔡遠利.基于改進蟻群算法的無人機路徑規劃[J].飛行力學，2017（1）：52-56.

[2]KARABOGA D.An idea based on honey bee swarm for numerical optimization[D].Erciyes：Erciyes University，2005.

[3]江銘炎，袁東方.人工蜂群算法及其應用[M].北京：科學出版社，2014.

[4]胡志忠，徐克虎，沈春林.低空突防用數字地形的平滑處理[J].南京航空航天大學學報，2000（5）：493-498.

[5]吳強，曹義華，金長江.最小飛行高度的計算[J].戰術導彈技術，2003（2）：21-24.

[6]嚴建林.基于進化算法無人機航路規劃技術研究[D].南京：南京航空航天大學，2008.

[7]MENONPKA，KIME，CHENGVHL.Optimal trajectory synthesis for terrain-following flight[J].Journal of Guidance Control and Dynamics，2012（4）：807-813.

[8]BONABEAU E，DORIGO M，THERAULAZ G.Swarm intelligence： from natural to Artificial systems[M].Oxford：Oxford University Press，1999.

[9]施法中.計算機輔助幾何設計與非均勻有理B樣條（修訂版）[M].北京：高等教育出版社，2013.