“云互動”環境下小學數學翻轉課堂實踐
——以《軸對稱圖形》教學為例

林永福

（興國縣長岡鄉中心小學，江西贛州 342431）

一、分析教材

《軸對稱圖形》是2013年人教版小學數學四年級下冊第七單元《圖形的運動（二）》的內容，在二年級下冊《圖形的運動（一）》中，學生已初步感知軸對稱圖形。而在四年級下冊《圖形的運動（二）》中，要求學生進一步認識軸對稱圖形，通過看一看、數一數，探索軸對稱圖形的特點和性質，并掌握補全軸對稱圖形的方法。

通常在教學這部分內容時，教師會分2個課時來完成，一是探究軸對稱圖形的特點和性質，二是學習補全軸對稱圖形的方法。學生已經在之前初步了解軸對稱圖形，并且有一定生活經驗，能夠較好地判斷哪些圖形是軸對稱圖形。“畫”是基于“感知”的基礎之上，如能正確、熟練地理解軸對稱圖形的特點，那么“畫”也就迎刃而解了。

二、“云互動”環境下的翻轉課堂實踐

（一）課前自學

1.設計分層課前任務單

所謂課前任務單，有別于以往的“導學案”，它不但是學生自學的指引，更是檢測自學效果的有效途徑。課前任務單主要包括，學習目標、學習方法和建議以及學習任務。在學習任務中，教師設計三個層次的檢測題。第一層次，復習舊知，認識軸對稱圖形，從指引性較強的填空、判斷題到動手剪、折軸對稱圖形的畫圖題，學生從表象感知過渡到實際理解；第二層次，探究新知，學生認真自學，根據“軸對稱圖形的特點”完成看圖填空題；第三層次，應用拓展題，“你能畫出與線段AB相對稱的圖形嗎”，此題考查學生對知識的理解和掌握程度。

2.二次備課

教師通過批改學生的課前任務單，了解學生對新知的掌握情況和存在問題，并結合學情，對課堂教學再次進行調整，有效地實現二次備課，真正落實以學定教。

（二）課堂鞏固

1.小組交流

在簡單的檢測后，對課前任務單中的重難點題目進行反饋。在之前的小組討論中，學生主要圍繞“平行四邊形到底是不是軸對稱圖形？正六邊形一共有幾條對稱軸？”這兩個問題進行討論，雖然在課前經歷了“剪—折—畫”的過程，但由于課前給孩子剪、折的是普通的平行四邊形，因而出現了其他有爭議性的觀點，如有學生提出：一些特殊的平行四邊形，比如長方形就屬于軸對稱圖形。為突破這一學習難點，教師在課前錄制了小視頻，在小組討論無法解決這一難點時，通過“云互動”平臺發布給學生，學生在個人平板電腦中自行觀看，通過直觀演示過程，學生發現：不是所有的平行四邊形都是軸對稱圖形，只有一些特殊的平行四邊形屬于軸對稱圖形。

2.互動提升

學生對軸對稱現象已有更進一步的理解。課堂教學中還需達成會應用“軸對稱的特點”的教學目標。教師設計“裝飾圣誕樹”的互動拓展題，將書中例1中的松樹文本加以修改，變“找對稱點”為“找相應的位置掛飾品”，學生則扮演起“小助手”的角色，同時充分利用“云互動”平臺，讓每一個學生動起手來，在平板電腦中自由拖動“飾品”，完成任務。

首先，教師出示已掛好的兩個飾品，請學生找出相對稱的位置掛飾品（圖1），學生根據“每組對稱點的距離到對稱軸相等”的特點找到相對稱的飾品位置。接著出示一組“笑臉”飾品，學生在互動平臺中自由選擇相對稱的位置掛飾品（圖2），這時，學生出現了不同的答案，教師可以通過互動平臺選取學生的作品進行分享，由學生互相點評。師生互動和生生互動，發現了許多有趣的觀點和細節，有時可能還會出現教師課前都未預設到的問題。

最后出示錯例（圖3），判斷這樣掛是否可以？通過與前面飾品的對比，學生最終發現，由于這樣的掛法，會導致兩個“笑臉”不在同一“水平線”上，即導致它們之間的連線與對稱軸不互相垂直，所以這樣掛“笑臉”是不對稱的。

通過三個層次的互動任務，原本“枯燥乏味”的數學知識，變得“生動有趣”，學生經歷了動手操作的活動，更透徹地理解“對稱點”的含義，也更熟練地掌握找對稱點的方法，對數學知識活學活用。

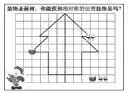
圖1

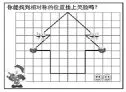
圖2

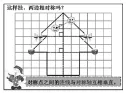
圖3

3.進階學習

根據教學目標，學生需根據給出的對稱軸，補全軸對稱圖形的另一半，那么筆者思考：既然是補全圖形，那么對稱軸既可以是豎著的，也可以是橫著的，還可以是斜著的。

教師出示書本例2的內容——補全星星圖（圖4）。學生自然而然想到要補全一個軸對稱圖形，最重要的是找到每條線段兩個端點的對稱點。此時，教師利用平板電腦，快速選拍學生的作品展示，再通過學生點評、對話交流，歸納補全軸對稱圖形的最優方法：一找關鍵點，二定對稱點，三連線。

緊接著出示圖5，當對稱軸時橫著的時候，教師再利用平板電腦選拍學生作品，并讓學生匯報自己的畫法。此時，有學生提出：把練習紙旋轉一下，使對稱軸變成豎著的，這樣就找對稱點了。教師課堂總結：解決問題的方法可以有多樣性，但萬變不離其宗，不管對稱軸是橫著還是豎著，都是先找關鍵點，再確定對稱點，最后連線。

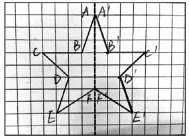
圖4

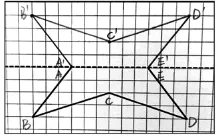
圖5

4.拓展應用

完成全部教學內容后，設計綜合檢測題，教師在圖中補畫一個小正方形，使它成為一幅軸對稱圖形（圖6）。此題綜合考查學生對軸對稱圖形的理解以及補全軸對稱圖形的方法等多個知識目標，發散思維，培養空間想象能力。同樣，教師采取平板電腦選拍的方式進行講評，通過作品展示，再一次感受軸對稱之美妙，學生思維得到碰撞和激發。

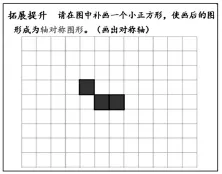
圖6

（三）課后思考

課堂學習應讓學生有所得，更應有所思。在前面的環節中，學生已認識到并不是所有的平行四邊形都屬于軸對稱圖形，那么可否將一個普通的平行四邊形通過各種軸對稱變換設計成一幅軸對稱圖形呢？課后思考題：自己確定對稱軸的位置，把下圖中的平行四邊形設計成一幅軸對稱圖形。學生可以根據自己的想法進行設計。開放性的思考題，不僅讓課程內容得到延續，讓學生得以應用操作，而且在這個學習過程中，內化知識，形成系統。