平行四邊形晶格結構中布里淵區的研究
左 謙,胡家光
(文山學院 信息科學學院,云南 文山 663099)
布里淵區,最早由法國物理學家萊昂·布里淵提出的。它是固體物理學中的重要概念,是電子能帶理論和表示晶體元激發的唯一構圖形式,它在晶體衍射、晶體振動、能帶理論等的研究中都起到極其重要的作用[1]。已往對布里淵區的大量研究多以方形晶格和正三角形晶格為例[2-5],本文的研究對象是平行四邊形晶格結構,研究平行四邊形晶格結構的意義在于:平行四邊形晶格結構是一種寬泛的結構模型,在電子晶體、光子晶體和聲子晶體中都廣泛存在,研究平行四邊形結構的布里淵區圖像,是研究這三類晶體能帶結構的基礎。且平行四邊形涵括了正方形、長方形、三角形、六邊形和普通平行四邊形幾種,通過改變平行四邊形晶格結構的邊長、角度,即可變換為眾多形狀,使得所研究的對象更為寬泛。本文詳細研究了平行四邊形晶格結構的第一布里淵區的形狀及所需的倒格矢,修正了劉頔威、劉盛綱的結論[6],完善了魏乃科等人[7]研究中對基矢模長比R大于的1的情況。
1 結構模型
二維平行四邊形晶格結構如圖1所示,其基矢為
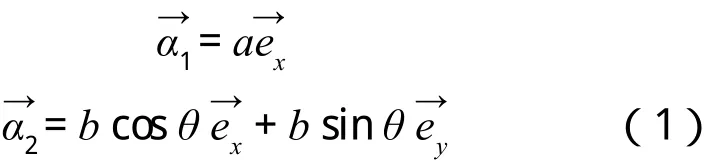
其中傾斜角θ是邊長a、b間的夾角(見圖1)。
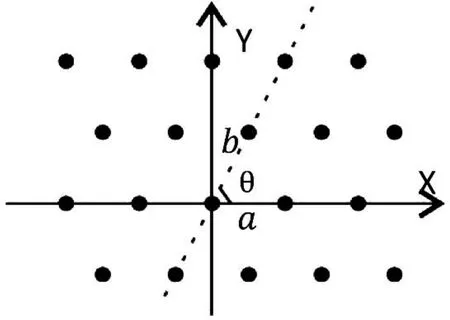
圖1 二維平行四邊形晶格結構圖
2 布里淵區
2.1 倒格矢的計算
倒格基矢公式:
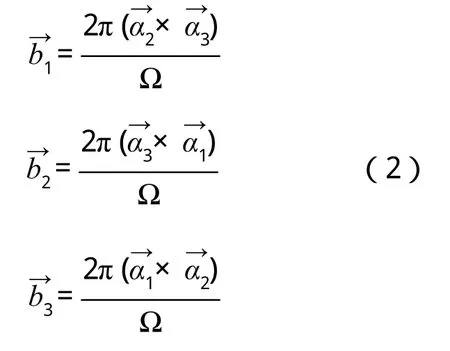
式中?是正格矢原胞體積,即:
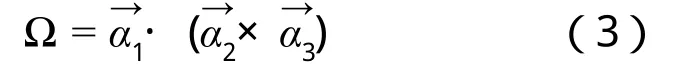
得出二維平行四邊晶格結構的正格矢原胞體積為

則二維平行四邊形晶格結構的倒格基矢公式為
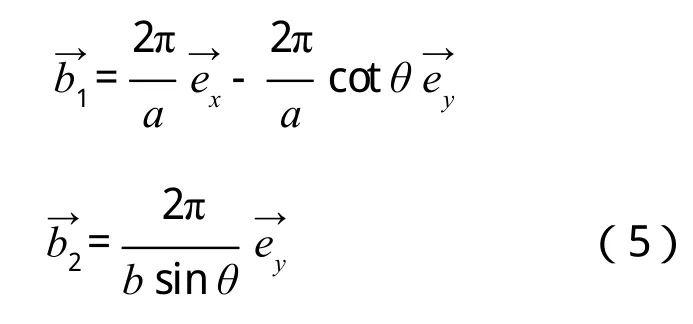
設倒格矢,則二維平行四邊形晶格結構中倒格矢為:

2.2 布里淵區圖像
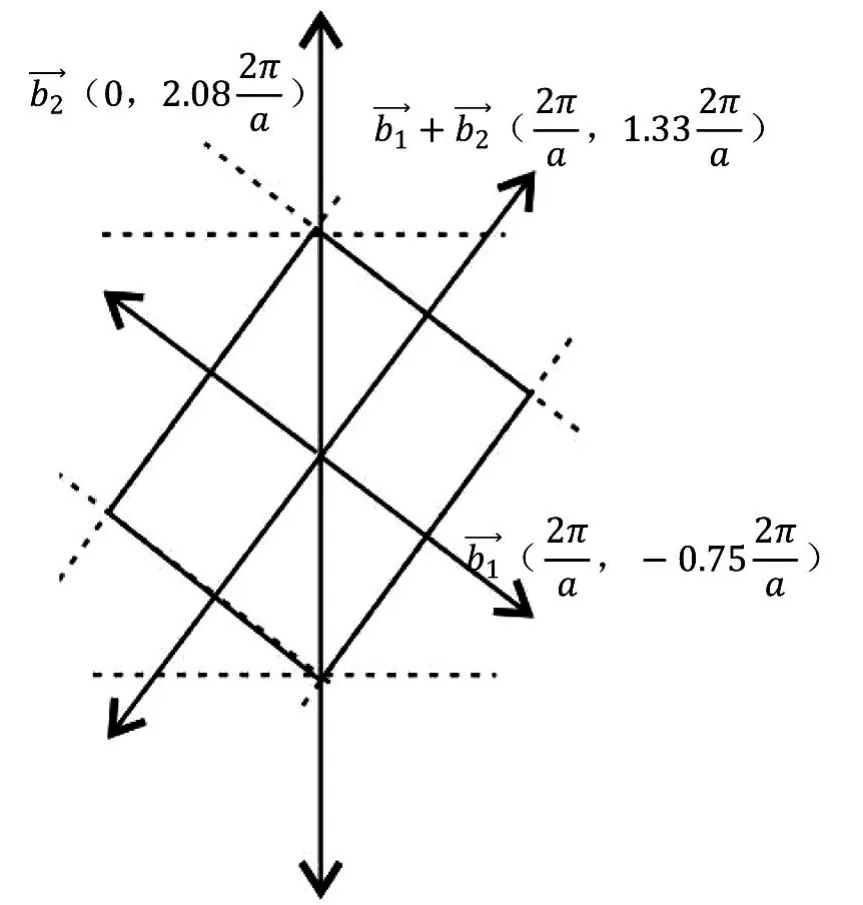
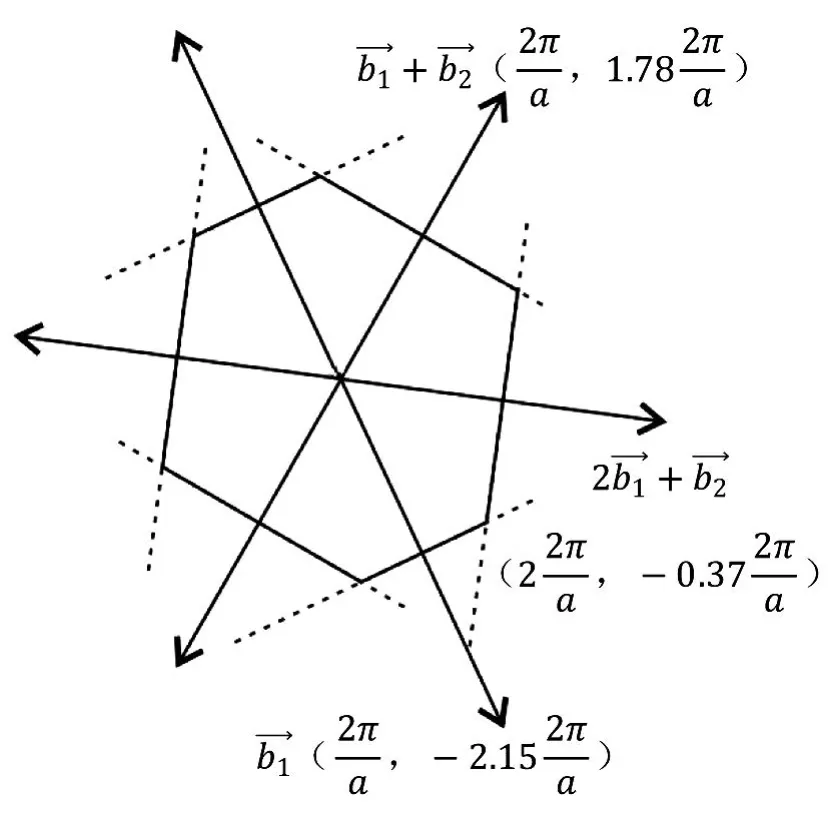
對于二維平行四邊形晶格結構,倒格矢)。布里淵區為這些中垂線所構成的圖形,形成的最小封閉區域即第一布里淵區[9]。令基矢模長比,則平行四邊形晶格在不同傾斜角下的第一布里淵區圖像如下:
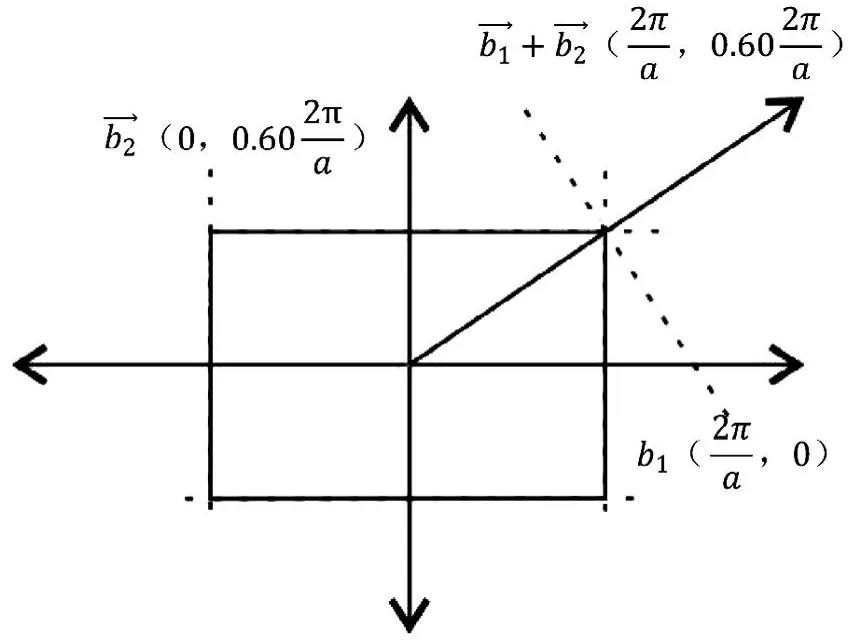
1)R取任意值(此處取為0.6),θ=90°
如圖2所示,倒格基矢為

通過這 4個矢量分別做 4條垂直平分線,即構成二維平行四邊形晶格結構(θ=90°)的第一布里淵區(見圖2)。
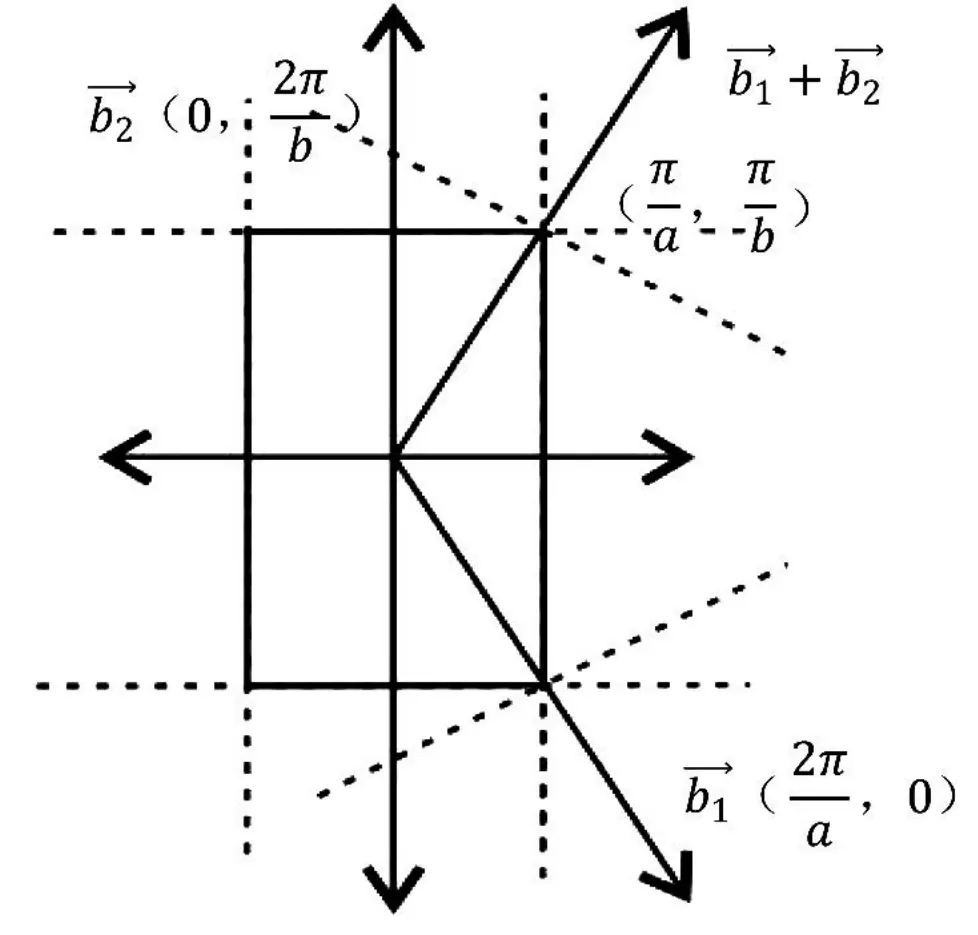
圖2 R任意,θ =90°的第一布里淵區圖像
2)R=1,θ< 90°(此處θ取 60°)
如圖3所示,倒格基矢為
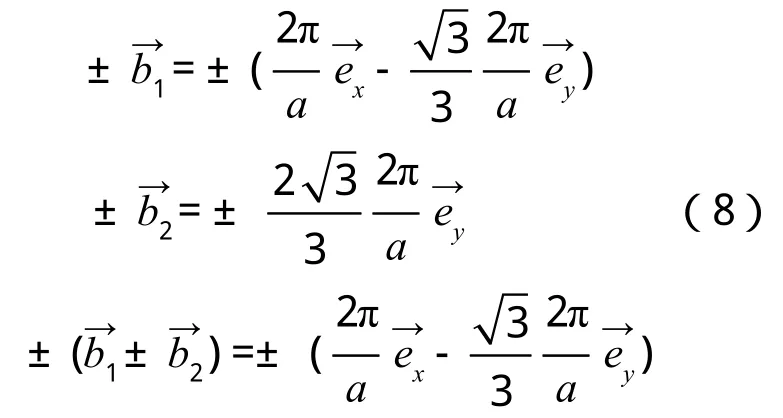
通過這 6個矢量分別做6條垂直平分線,即構成二維平行四邊形晶格結構(θ=60°)的第一布里淵區(見圖3)。
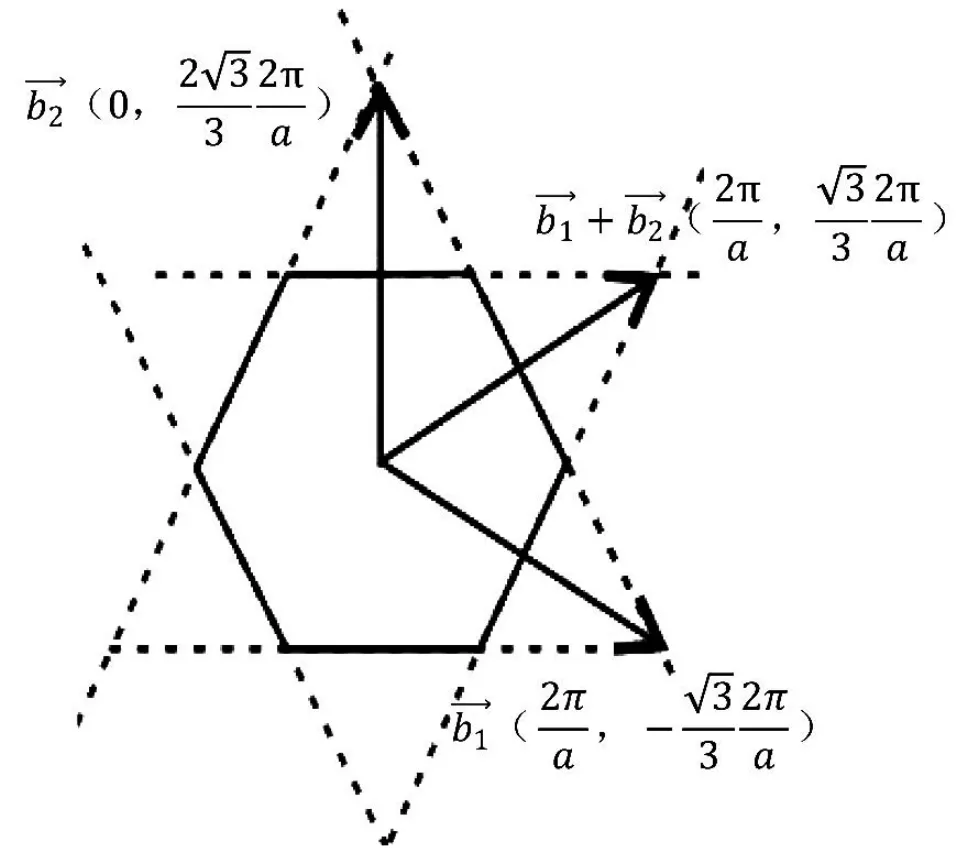
圖3 R=1,θ=60°的第一布里淵區圖像
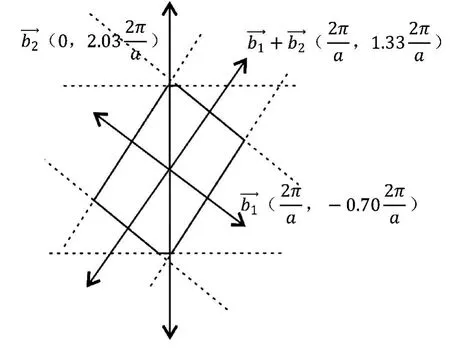
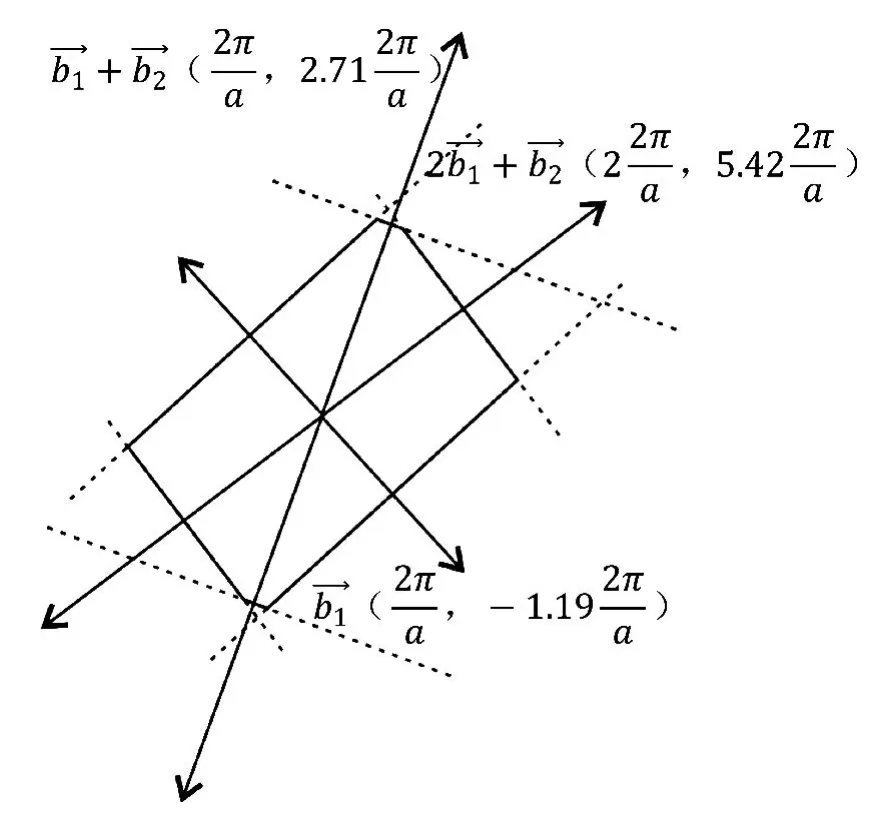
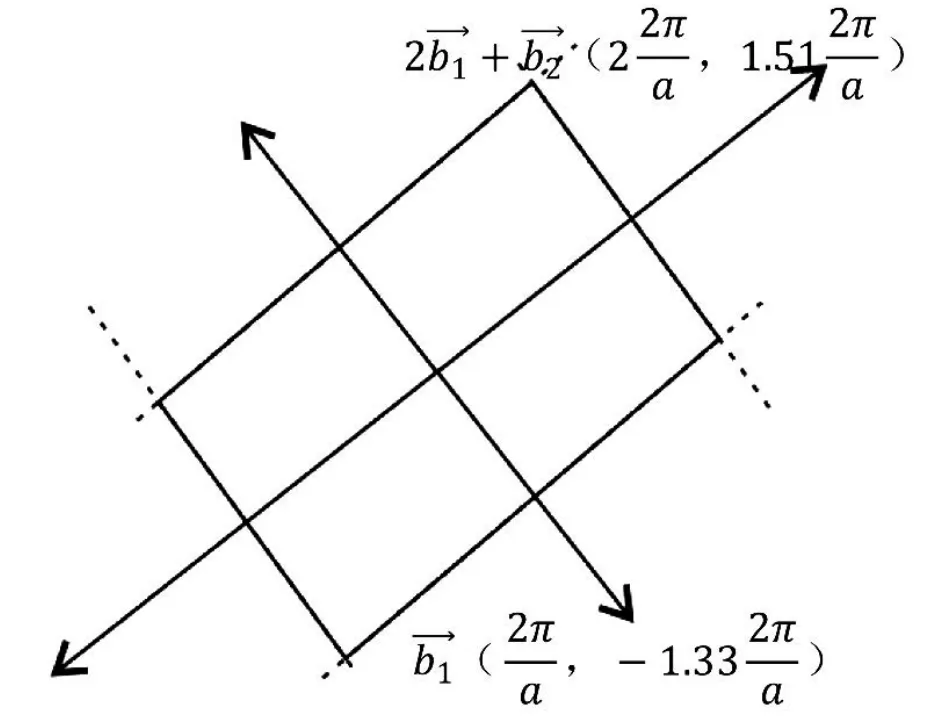
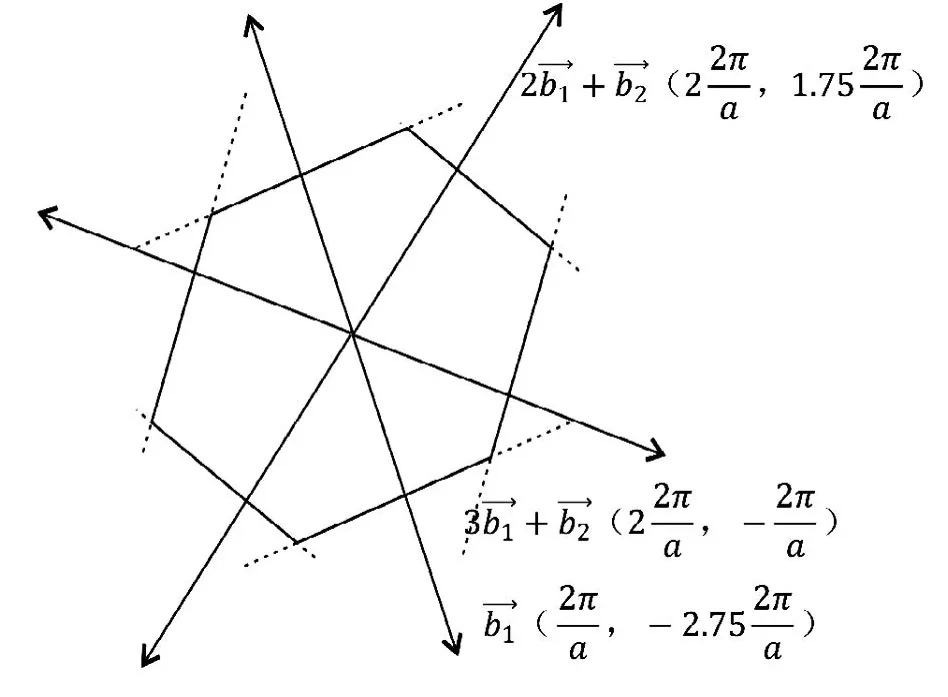
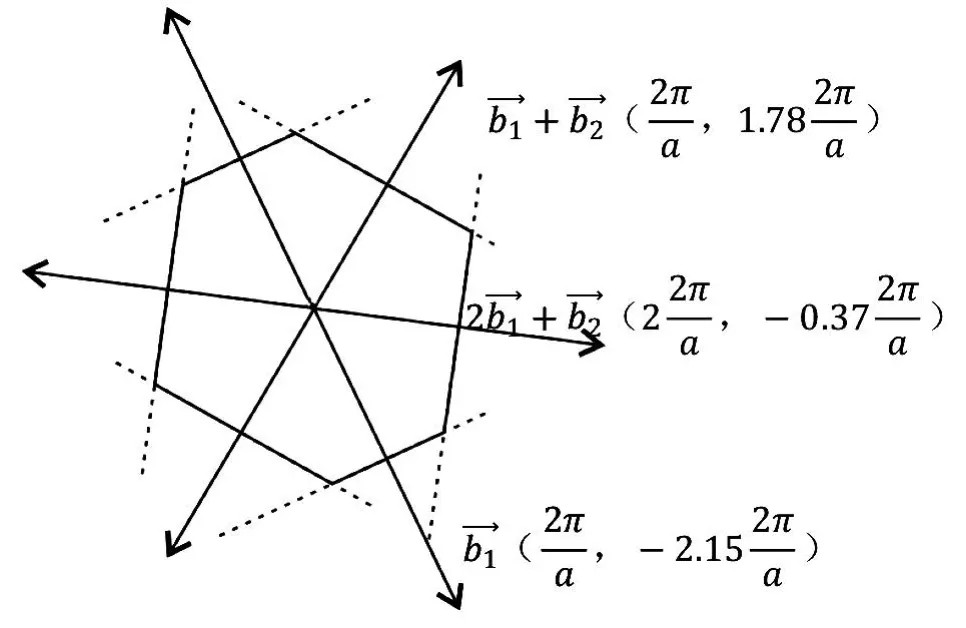
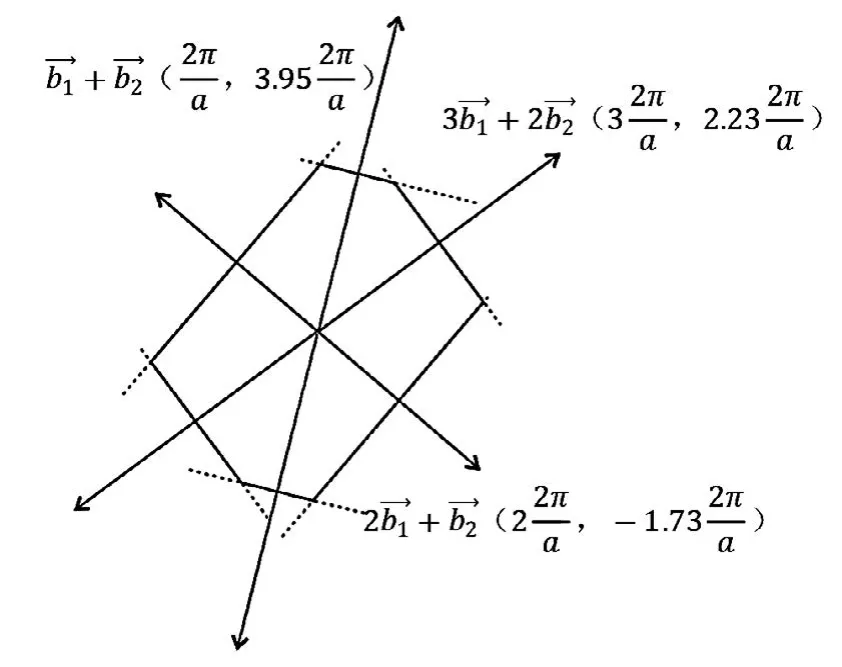
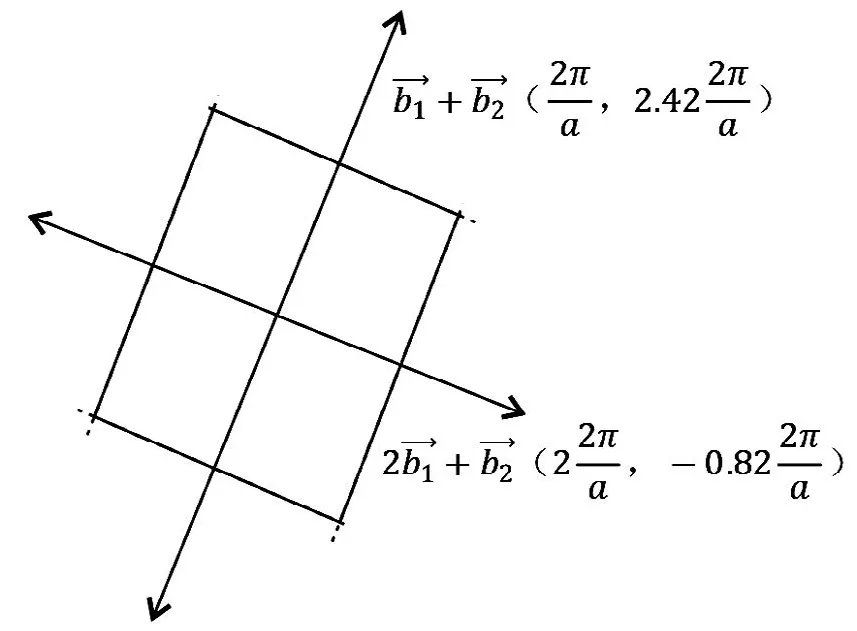
3)R<1,cosθ 如圖4所示,倒格基矢為 通過這六個矢量分別做6條垂直平分線,即構成二維平行四邊形晶格結構(θ=55°)的第一布里淵區(見圖4)。 圖4 R=0.6,θ=55°的第一布里淵區圖像 4)R<1,cosθ=R(此處取R=0.6,θ=53.1°) 如圖5所示,倒格基矢為 通過這 6個矢量分別做 4條垂直平分線,即構成二維平行四邊形晶格結構(θ=53.1°)的第一布里淵區(見圖5)。 圖5 R=0.6,θ=53.1°的第一布里淵區圖像 5)R<1/2,R 如圖6所示,倒格基矢為 由分別做 6條垂直平分線,即構成二維平行四邊形晶格結構(θ=40°)的第一布里淵區(見圖6)。 圖6 R=0.4,θ=40°的第一布里淵區圖像 6)R<1/2,cosθ=2R(此處取R=0.4,θ=36.87°) 如圖7所示,倒格基矢為 由分別做4條垂直平分線,即構成二維平行四邊形晶格結構(θ=36.87°)的第一布里淵區(見圖7)。 圖7 R=0.4,θ=36.87°的第一布里淵區圖像 7)R<1/2,2R< cosθ< 3R(此處取R=0.4,θ=20°) 如圖8所示,倒格基矢為 由分 別 做 6條垂直平分線,即構成二維平行四邊形晶格結構(θ=20°)的第一布里淵區(見圖8)。 圖8 R=0.4,θ=20°的第一布里淵區圖像 8)1/2 如圖9所示,倒格基矢為 由)分 別 做 6條垂直平分線,即構成二維平行四邊形晶格結構(θ=25°)的第一布里淵區。 圖9 R=0.6,θ=25°的第一布里淵區圖像 9)1/2 如圖10所示,倒格基矢為 由分別做 4條垂直平分線,即構成二維平行四邊形晶格結構(θ=17.15°)的第一布里淵區(見圖10)。 圖10 R=0.6,θ=17.15°的第一布里淵區圖像 10)(此處取R=0.6,θ=10°) 如圖11所示,倒格基矢為 由)分別做 6條垂直平分線,即構成二維平行四邊形晶格結構(θ=10°)的第一布里淵區(見圖11)。 圖11 R=0.6,θ=10°的第一布里淵區圖像 11)R> 1,θ=90°,(此處取R=1.67) 如圖12所示,倒格基矢為 由分別做 4條垂直平分線,即構成二維平行四邊形晶格結構(θ=90°)的第一布里淵區(見圖12)。 圖12 R=1.67,θ=90°的第一布里淵區圖像 12)R> 1,θ=90°,(此處取R=1.67,θ=60°) 如圖13所示,倒格基矢為 由)分別做 6條垂直平分線,即構成二維平行四邊形晶格結構(θ=60°)的第一布里淵區(見圖13)。 圖13 R=1.67,θ=60°的第一布里淵區圖像 13)R> 1,cosθ=R,(此處取R=1.67) 因為R> 1時,cosθ無法取值,故而將R的取值轉化為1/R,即取cosθ=1/R(此處θ取53.1°) 如圖14所示,倒格基矢為 通過這 6個矢量分別做6條垂直平分線,即構成二維平行四邊形晶格結構(θ=53.1°)的第一布里淵區(見圖14)。 圖14 R=1.67,θ=53.1°的第一布里淵區圖像 (14)R> 1,R< cosθ=3R,(此處取R=1.67,θ=25°) 因為R> 1時,cosθ無法取值,故而將R的取值轉化為1/R。 如圖15所示,倒格基矢為 由分別做6條垂直平分線,即構成二維平行四邊形晶格結構(θ=25°)的第一布里淵區(見圖15)。 圖15 R=1.67,θ=25°的第一布里淵區圖像 通過計算二維平行四邊晶格結構的倒格矢,并詳細推導出不同角度下對第一布里淵區有貢獻的具體倒格矢,畫出了不同傾斜角的第一布里淵區形狀。通過對布里淵區形狀的分析可知,當θ=90°,對R任意取值,倒格矢正交,其中垂線圍成矩形,的中垂線剛好經過矩形的頂點,所以此條件下第一布里淵區為矩形。減小的中垂線圍成平行四邊形,與的中垂線相交,第一布里淵區為平行六邊形。繼續減小傾斜角θ,當cosθ=R時,倒格矢正交,第一布里淵區為矩形。繼續減小θ,正交臨界條件則被破壞,中垂線所構成的平行四邊形與的中垂線相交,形成的第一布里淵區形狀為平行六邊形。減小θ使之滿足cosθ=(2R2+1)/3R,則再次出現正交臨界條件,第一布里淵區由的中垂線正交構成矩形。再次減小θ,正交臨界條件又會被破壞,形成平行六邊形,等θ的取值滿足又一正交臨界條件時,則再次形成矩形。因而根據倒格矢正交臨界條件即可對θ不同時,二維平行四邊形晶格結構的布里淵區進行劃分歸類(見表1)。 本文也對基矢模長比R> 1的情況進行了取值畫圖,分析發現,當R> 1,cosθ的取值與R相關聯的時候(例如cosθ=R),無法對cosθ進行取值,此時若將R的取值轉化為1/R,則可繼續開展工作,此情況下的倒格矢與R< 1時相對應的倒格矢無異。故而R> 1時,將R替換為1/R即可。 本文對任意角度下的二維平行四邊形晶體結構的倒格矢進行了詳細推導,對其第一布里淵區的圖像進行了繪制,主要結果如下: 1)第一布里淵區與傾斜角及基矢模長比R緊密相關,在基矢模長比R不變的情況下,改變傾斜角,第一布里淵區的圖像將在矩形和平行六邊形之間交替變化,所需的倒格矢也相應地變化。在正交臨界條件下構成矩形,在倆個正交臨界條件之間所構成的圖形均為平行六邊形。故而可依正交臨界條件對二維平行四邊形晶體結構的第一布里淵區進行劃分。 2)對于基矢模長比大于1的情況,因無法對cosθ進行取值,故而可將R轉化為1/R進行計算推導,結果不變。 表1 第一布里淵區的劃分 [1]吳越,胡經國.布里淵區和費米面[J].揚州工學院學報,1991(2):56-59. [2]王矜奉.固體物理教程[M].第八版.山東:山東大學出版社,2013:11-14,170-175. [3]李進,李光惠.布里淵區與倒格子原胞[J].大學物理,1997(1):29-31. [4]邵華圣.關于第n布里淵區體積等于倒格子原胞體積的證明[J].大學物理,2009(1):54-56. [5]莎仁.固體物理學中布里淵區概念在方法論上的意義[J].內蒙古師大學報(自然科學版),1988(4):54-58. [6]劉頔威,劉盛綱.二維單斜點陣光子晶體的第一布里淵區及帶隙計算[J].物理學報,2007(5):2747-2748. [7]魏乃科,朱建華,馬文英,姚軍.二維斜方晶格光子晶體的第一布里淵區分析[J].光散射學報,2010(1):20-22. [8]易明芳.關于物理能帶論中布里淵區的注記[J].安慶師范學院報(自然科學版),2005(4):75-77. [9]雷善云.談怎樣才能做好布里淵區[J].貴州師大學報(自然科學版),1990(2):74-76.
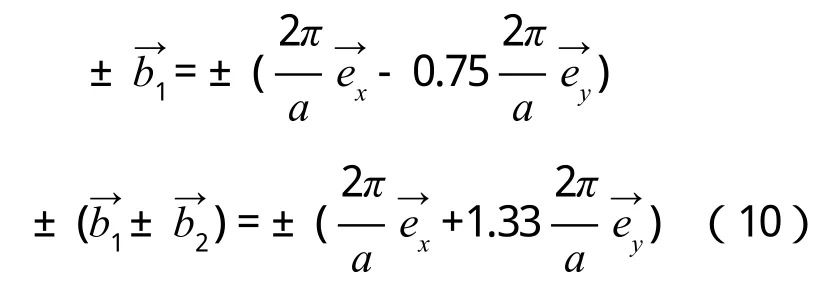


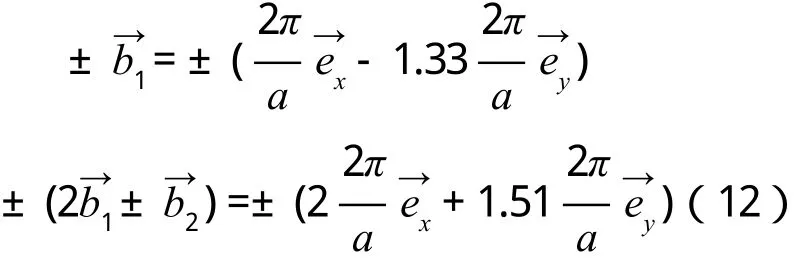
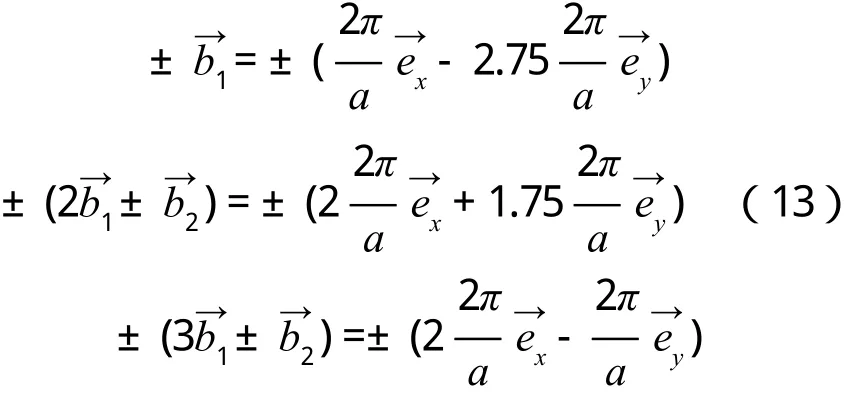
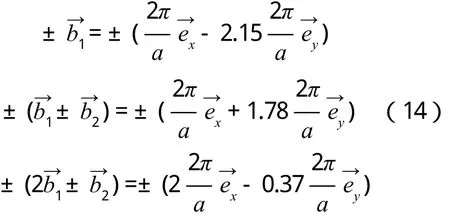
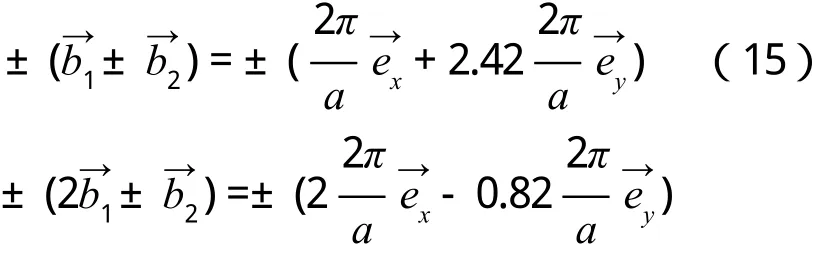
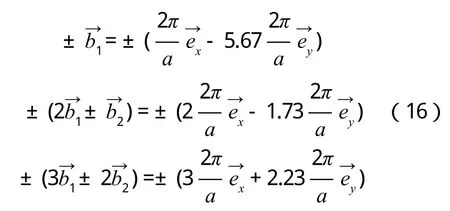
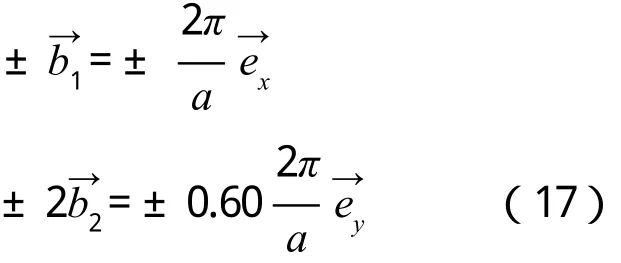
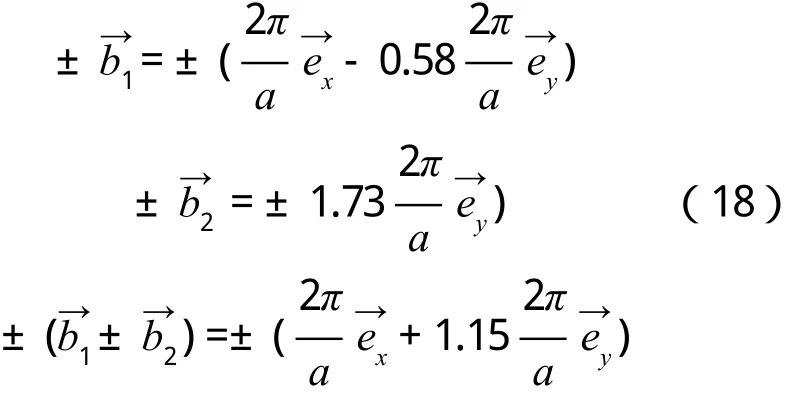

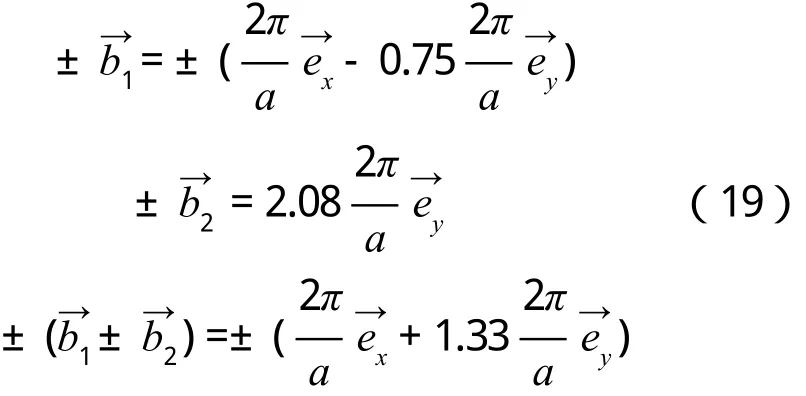

2.3 歸類總結
3 結論


