基于航空器優先級的場面航空器動態滑行優化*
賈 媛 姜 雨 徐 成 蔡夢婷
(南京航空航天大學民航學院 南京 211106)
0 引 言
近年來,我國航空運輸業發展迅速,機場樞紐化趨勢日益明顯,航空運輸系統的運行和管理壓力與日俱增.針對航班延誤和機場擁堵現象日益嚴重的現狀,提高機場場面資源的運行效率,增加場面容量已經迫在眉睫.
目前國內外學者對航空器場面滑行優化的研究主要分為靜態和動態兩個方面.在航空器靜態場面滑行優化方面,利用混合整數線性規劃(MILP)方法[1]、遺傳算法(GA)[2]、改進的A*算法[3]等智能算法,得到基于固定路徑的滑行路徑優化序列.在航空器動態場面滑行優化方面,一部分學者通過利用復雜網絡[4]、遺傳算法[5]、元胞自動機(CA)[6]、改進的粒子群算法(CPSO)[7]、主動路由選擇(AR)[8]、混合整數規劃(MIP)方法[9-10]、改進的蟻群算法[11]、多目標免疫優化算法[12]等智能算法,對航空器場面滑行進行動態優化;另一部分學者對模型進行改進,例如,建立跑道和滑行道聯合調度的集成優化模型[13],建立多目標多分枝的航空器場面滑行優化模型[14-15]等.
縱觀國內外研究成果,學者們已經從滑行效率和安全兩個角度進行航空器動態滑行優化研究,并取得一定成果.但是隨著研究的深入,航空器屬性,尤其是航空器優先級,越來越成為影響滑行效率和安全的關鍵因素.因此,如何從優先級角度出發,提高航空器滑行效率和安全,降低場面擁堵,緩解運行壓力已經勢在必行.
本文以最小化所有進離場航空器運行成本為目標,建立基于航空器優先級的場面航空器動態滑行優化模型.探討航空器優先級的確定方法,設計滑行沖突解決策略,引入滾動時域方法進行求解.使用MATLAB仿真平臺,驗證該優化方案的可行性和有效性.
1 基于航空器優先級的滑行沖突解決策略
1.1 航空器優先級的確定
航空器優先級的確定考慮三個因素:時間優先、機型優先、延誤優先.三種優先級的高低順序分別為:時間優先>機型優先>延誤優先.
“時間優先”是指根據航班時刻表,預計起飛時間早的航空器比預計起飛時間晚的航空器具有優先級.這樣設定優先級,原因為:①航班時刻表相對固定,為保證旅客權益,以及考慮到旅客的滿意度,一般不允許航空器提前起飛而造成旅客誤機;②不同的航班屬于不同的航空公司,不能僅憑機型來決定由哪家航空公司來承擔延誤損失,考慮到航空公司之間的公平性,只有按照航班時刻表才能保證相對公正,畢竟航班時刻表是各航空公司、空管單位和其他相關部門之間利益平衡的結果.
“機型優先”是指根據《國際民用航空公約》的相關規定和場面航空器運行的實際情況,航空器優先級的確定是由航空器的屬性(如專機、故障機、貨機等)、機型成本率、載客數、平均耗油率等參數決定.“機型成本率”主要由該機型載客數和平均耗油率這兩項主要性能指標確定.“載客數”是估計該機型單位時間內旅客地面等待成本的重要參數,“平均耗油率”是估計該機型在發動機工作時運行成本的重要參數.其他一些因素,如公司信譽、人員工作負荷、飛機維護成本等,可以將其折算到單位乘客等待成本或者航油價格中去.
“延誤優先”是指延誤航班的優先級低于正常航班的優先級,其中“延誤航班”是指在航班時刻表預定的起飛時間15 min后還未能起飛的航班.同時,在所有延誤航班內部仍然按照時間優先和機型優先順序來確定各航空器的優先級.
1.2 航空器滑行沖突解決策略
本文提出的沖突解決策略是通過判斷沖突航空器的優先級,優先級高的航空器可以按原計劃路徑直接通過沖突區域,按原路徑繼續滑行;優先級低的航空器有兩種滑行方案可選:①進入沖突區域前減速等待;②提前選擇次優可替代滑行路徑(一條不經過沖突區域且到達終點的最短路徑).
設航空器的優先級為p,航空器選擇減速等待的最短等待時間為Δt,航空器單位時間滑行成本與單位時間等待成本之比為λ,最短滑行路徑與次優可替代滑行路徑的長度之差為替代成本Δc,平均滑行速度為v.分別計算兩種滑行方案的滑行時間成本:①進入沖突區域前減速等待,將最短等待時間Δt乘以滑行成本與等待成本之比λ,轉換為滑行時間成本λΔt;②提前選擇次優可替代滑行路徑,將替代成本Δc除以滑行速度v,轉換為滑行時間成本Δc/v.將Δc/v與λΔt進行比較,選擇較小的滑行時間成本,進而選擇合理的沖突解決策略,實現所有進離場航空器無沖突滑行且運行成本最小化的目標.當滑行沖突無法通過減速等待或選擇次優可替代滑行路徑解決時,即發生死鎖狀況.當發生死鎖時,可不嚴格執行優先級策略,臨時交換航空器的優先級,再按相應的沖突解決方法來解決沖突.沖突解決之后,恢復航空器各自的優先級.
2 基于航空器優先級及滑行沖突解決策略的滑行優化模型
2.1 模型假設
1) 航空器勻速滑行,并且速度不能超過機場規定的最大速度55 km/h.
2) 航空器間距符合規定的最小安全間距20 s.
3) 進離場航空器滑行路徑連續.
4) 在研究時段內,所有進離場航空器相關信息、標準坐席數、滑行油耗等信息己知.
5) 航空器滑行優化動態連續,本文只研究某一時段T內所有航空器的滑行優化.
2.2 定義符號及變量



2.3 目標函數
(1)
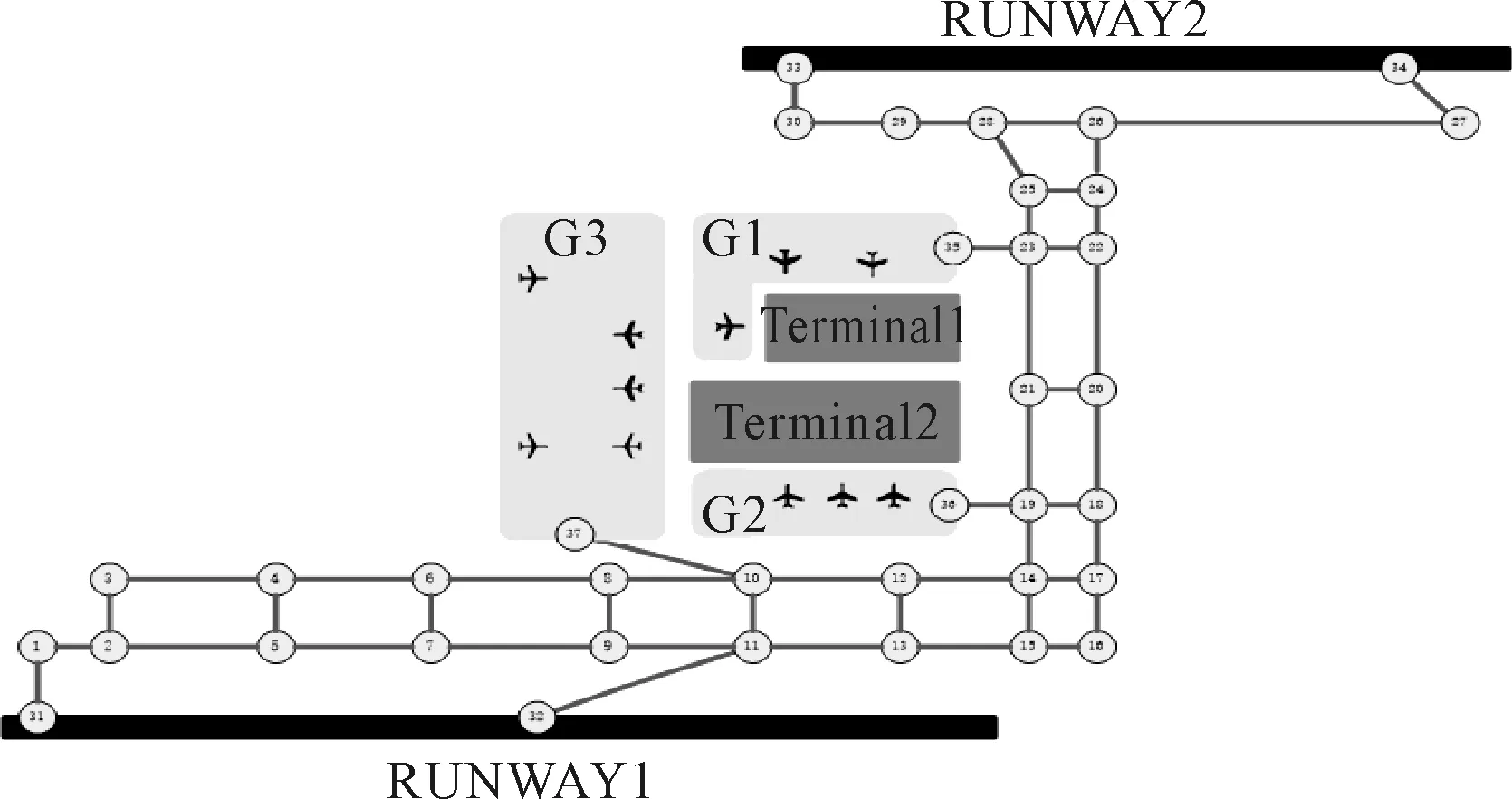
式中:Z1為滑行距離目標函數;Z2為滑行等待時間目標函數;pi 當λiΔti>Δci/ti時,低優先級航空器fi選擇次優可替代滑行路徑,繞過沖突區域,考慮其增加的滑行距離,滑行成本目標函數Z轉化為滑行距離目標函數Z1,最小化研究時段內所有進離場航空器的滑行距離,其表達式為 (2) 當λiΔti<Δci/ti時,低優先級航空器fi選擇減速等待,考慮其增加的滑行等待時間,滑行成本目標函數Z轉化為滑行等待時間目標函數Z2,最小化研究時段內所有進離場航空器的滑行等待時間,其表達式為 (3) 式中:(Tidi-TBTi)為航空器fi從最早可開始滑行時間起到達目的地所花費的實際時間;(tidi-tioi)為航空器fi從最早可開始滑行時間起到達目的地無沖突滑行的最短時間. ?fi∈F,?np,nq∈N (4) ?p,q,s∈N (5) ?p,q∈N (6) (7) (8) (9) (10) (11) (12) (13) 式(4)為滑行路徑需符合滑行道容量要求,滿足物理鏈接性;式(5)為滑行路徑需連續可行,滿足流動平衡性;式(6)為滑行速度約束;式(7)為安全間隔約束.式(8)~(9)為對頭沖突約束.式(10)~(11)為超越沖突約束.式(12)為高優先級航空器優先滑行的調度原則.式(13)為所有航空器要在開始滑行時間之后才能開始滑行. 滾動時域方法是一種時間分解法,將一個全局大規模優化問題分解為一系列相關聯的小規模優化子問題,計算復雜度大大降低,且子問題部分利用全局信息,調度質量明顯提高[16].基于滾動時域的航空器場面動態滑行優化模型求解過程如下: 步驟1設調度開始時刻為t0,則ti=t0. 步驟2設在ti時刻,預測時域為Γ,選擇調度時域[ti,ti+Γ]內將要開始滑行和正在滑行的航空器組成預測窗口,實時更新航空器的動態信息. 步驟3獲取航空器信息,根據Dijkstra最短路算法,求出預測窗口內各航空器的理想滑行路徑. 步驟4在計劃時域窗口T內形成滑行調度子問題.子問題的目標函數和約束條件同原問題,除新加入的航空器外,還包括上一計劃時域窗口未完成滑行的航空器,其開始滑行時間和地點為上一計劃時域結束時的狀態. 步驟5確定滾動窗口長度m,完成調度的航空器數量n,進行迭代滾動.在滾動窗口內航空器按照其理想滑行路徑滑行,若遇到沖突,則沖突解決策略確定等待時間或其他滑行路徑.直到該計劃時域窗口航空器數量不足n時,結束當前調度. 步驟6ti+1=ti+T,i=i+1,若ti<Γ,轉步驟2,否則求解結束. 選取我國某大型機場作為研究對象,為方便起見,選取該機場西半區域,將多個相鄰停機位抽象成三個集中停機區G1、G2和G3,去掉一些無關滑行道和節點,形成包含37個節點、48條邊、2條跑道和3個集中停機區的網絡圖,見圖1. 圖1 我國某大型機場西半區域滑行道系統部分構型圖 航空器數據選取該機場2016年7月某天08:00-08:15內的高峰小時航班數據,見表1. 表1 我國某大型機場研究時段內進離場航空器相關信息 本文使用滾動時域方法求解模型時,具體參數設置如下:高峰時段內預測窗口航空器數量為16架,計劃時域窗口T為3 min,即180 s,由Dijkstra最短路徑算法求得的航空器理想滑行路徑集可知,最后一架航空器完成調度的時間是1 094 s,|1 094/180|=7(向上取整),則共有7個調度時域窗口,形成7個調度子問題.求解這7個調度子問題,得出在基于理想滑行路徑的調度方案下,航空器沖突點的總個數為11個,共有6對航空器發生沖突.本文的算法設計就是建立在理想調度的基礎上,通過基于航空器優先級的沖突解決策略動態處理滑行沖突,以此保證航空器滑行安全并最小化滑行成本. 通過采用滾動時域方法,對研究時段內的16架航空器進行基于航空器優先級的場面滑行優化仿真.優化后的滑行路徑集避免了11處滑行沖突.為體現本文優化算法的優越性,增加基于先到先服務(FCFS)的固定路徑下的調度結果作為比較,調度結果對比見圖2. 圖2 基于FCFS與基于優先級調度結果對比圖 分別比較基于理想滑行路徑、基于FCFS的固定路徑滑行和基于航空器優先級的動態路徑滑行的總等待時間、總滑行距離、總替代成本和沖突數,結果見表2. 表2 三種不同優化方案的結果對比 綜合比較三種方案的優化結果,在理想滑行路徑的優化方案下,各航空器選擇最短滑行路徑到達其終點,過程中無需等待,但這必然造成滑行沖突.在本仿真中,沖突點的總個數為11個.而在實際滑行過程中,不允許有滑行沖突點存在.雖然后兩種優化方案都能解決滑行沖突問題,但是付出的代價卻不同. 由圖2和表2可知, 基于航空器優先級的動態路徑滑行方法的結果顯著優于基于FCFS的固定路徑滑行方法,這是因為前者可以通過運行沖突解決機制,令優先級較低的航空器選取次優可替代滑行路徑,或者減速等待來規避沖突,并選取成本較低的方法完成滑行;而后者無法選擇較短路徑,只能通過減速等待方式避免沖突,所以無論是在滑行路徑長度上還是在等待時間上,基于航空器優先級的動態路徑滑行方法都優于基于FCFS的固定路徑滑行方法. 在航空器的滑行過程和沖突解決過程中,都必須考慮航空器的優先級,本文提出的基于航空器優先級的動態滑行優化算法能夠確保當發生滑行沖突時,優先保障優先級高的航空器的滑行,見表3. 由表3得知,當發生滑行沖突時,在基于航空器優先級的優化方法下,保障了所有優先級高的航空器的優先權.而FCFS方法根據到達時間調度,只有航空器3,15,14在遇到滑行沖突時是因其先到達滑行區域而優先滑行的,并不能保障優先級高的航空器能夠優先滑行.故本文提出的基于航空器優先級的優化能夠保證優先級高的航空器優先滑行,符合實際情況. 表3 航空器優先級保障 在沖突方面,若所有航空器采用理想滑行路徑滑行,將存在11個沖突點,采用基于FCFS的固定路徑滑行和基于航空器優先級的動態路徑滑行都不存在沖突點,但是其解決沖突的方式有所差異. 圖3為超越沖突解決策略過程分析圖,由圖3可知,當提前檢測到航空器3和航空器4在滑行道(4,3)段發生超越沖突時,基于FCFS的固定路徑滑行方法是令后機(航空器3)降低滑行速度,不改變其原來的滑行路徑,跟隨前機,增加了后機的等待時間.而基于航空器優先級的動態路徑滑行方法是令后機提前在節點6處選擇次優可替代滑行路徑6-7-5-2通過沖突區域,到達滑行終點.有效避免滑行沖突,無需進行等待,不增加滑行距離. 圖3 超越沖突解決策略過程分析圖 圖4為交叉點沖突解決策略過程分析圖,由圖4可知,當提前檢測到航空器14跟航空器16在節點14處將發生交叉點沖突時,基于FCFS的固定路徑滑行方法是令后到達的航空器16在到達節點14前等待18.2 s,以使兩架航空器滿足最小安全間隔要求.而基于航空器優先級的動態路徑滑行方法是令航空器16提前在節點15處選擇次優可替代路徑15-16-17通過沖突區域,繞行距離160 m,用時13.3 s,小于18.2 s,由此可見本文動態滑行的優越性. 圖4 交叉點沖突解決策略過程分析圖 本文基于航空器優先級的動態路徑沖突解決策略明顯優于基于FCFS的固定路徑沖突解決策略,主要區別在于后者僅考慮到前后兩架航空器到達沖突區域(滑行道節點或路段)時間順序,令先到達沖突區域的航空器優先通過,而沒有考慮到航空器的機型、任務性質、突發狀況等方面,這不符合場面實際運行情況,不利于航空公司控制運行成本,也不利于機場提高場面運行效率.而本文提出的基于航空器優先級的動態路徑沖突解決策略克服了FCFS方法的種種缺點,可以有效緩解大型樞紐機場場面運行效率無法滿足實際運行需求的現狀,增加場面容量. 本文結合準確的機場場面網絡結構,以最小化研究時段內所有進離場航空器滑行成本為目標,建立基于航空器優先級的大型機場場面航空器動態滑行優化模型,探討了場面滑行優化中航空器優先級的確定方法,提出基于航空器優先級的滑行沖突解決策略,在保證航空器優先級和滑行安全的前提下最小化滑行成本,為大型機場場面航空器的動態滑行提供符合實際運行情況的優化理論與方法. 在此研究基礎上,未來可進一步考慮航空公司間的公平性、航空器碳排放等因素,對大型機場場面航空器動態滑行進行更深層次的研究. 參考文獻 [1] SMELTINK J W, SOOMER M J, WAAL P R D, et al. An optimisation model for airport taxi scheduling [J]. Mathematical Problems in Engineering,2008(1):55-58. [2] DEAU R, GOTTELAND J B, DURAND N. Airport surface management and runways scheduling[J]. Transportation Research Part C: Emerging Technologies ,2009(2):478-482. [3] ZHOU H, JIANG X. Research on taxiway path optimization based on conflict detection [J]. Plos One, 2014,10(7):897-901. [4] LANDRY S J, CHEN X W, NOF S Y. A decision support methodology for dynamic taxiway and runway conflict prevention[J]. Decision Support Systems, 2013,55(1):165-174. [5] JIANG Y, LIAO Z, ZHANG H. A collaborative optimization model for ground taxi based on aircraft priority[J]. Mathematical Problems in Engineering, 2013(2):1-9. [6] MORI R. Aircraft ground-taxiing model for congested airport using cellular automata[J]. Intelligent Transportation Systems, IEEE Transactions on, 2013,14(1):180-188. [7] JINGNAN Z. Airport taxi scheduling strategy based on particle swarm optimization algorithm[J]. 2014. [8] WEISZER M, CHEN J, STEWART P. A real-time active routing approach via a database for airport surface movement[J]. Transportation Research Part C: Emerging Technologies, 2015,58:127-145. [9] GUéPET J, BRIANT O, GAYON J P, et al. The aircraft ground routing problem: analysis of industry punctuality indicators in a sustainable perspective[J]. European Journal of Operational Research, 2016,248(3):827-839. [10] 張天慈,丁萌,左洪福,等.基于區域控制的航空器滑行軌跡優化模型[J].系統工程與電子技術,2016,38(1):136-141. [11] 高加凱.基于廣州白云機場平行跑道航空器滑行路徑優化研究[D].德陽:中國民用航空飛行學院,2017. [12] 王湛,熊佳俊,陳浩.航空器場面滑行速度與油耗研究[J].武漢理工大學學報(交通科學與工程版),2017,41(3):391-394. [13] YU C. Integrated optimization of airport taxiway and runway scheduling[J]. Journal of Automation and Control Engineering ,2014(4):578-586. [14] RAVIZZA S, CHEN J, ATKIN J A D, et al. Aircraft taxi time prediction: Comparisons and insights[J]. Applied Soft Computing, 2014,14:397-406. [15] CHEN J, WEISZER M, ATKIN J, et al. A heuristic approach to greener airport ground movement[J]. European Journal of Operational Research,2014(3):587-596. [16] 王冰.滾動時域調度方法及其性能分析研究[D].上海:上海交通大學,2005.2.4 約束條件
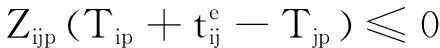
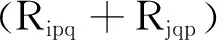
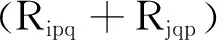




3 基于滾動時域的模型求解過程
4 仿真算例

4.1 仿真結果分析

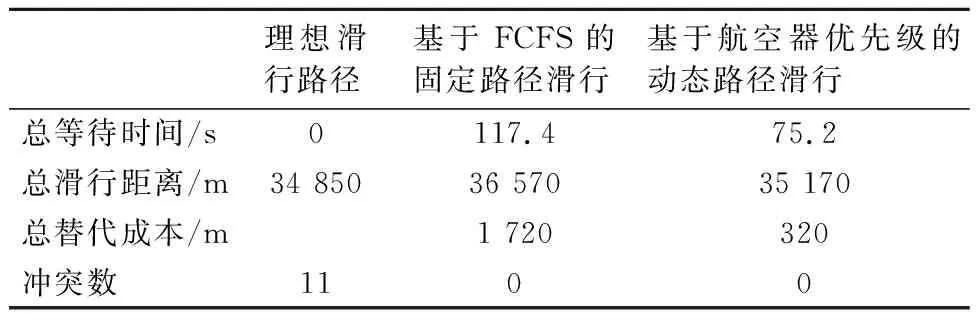
4.2 優先級保障分析
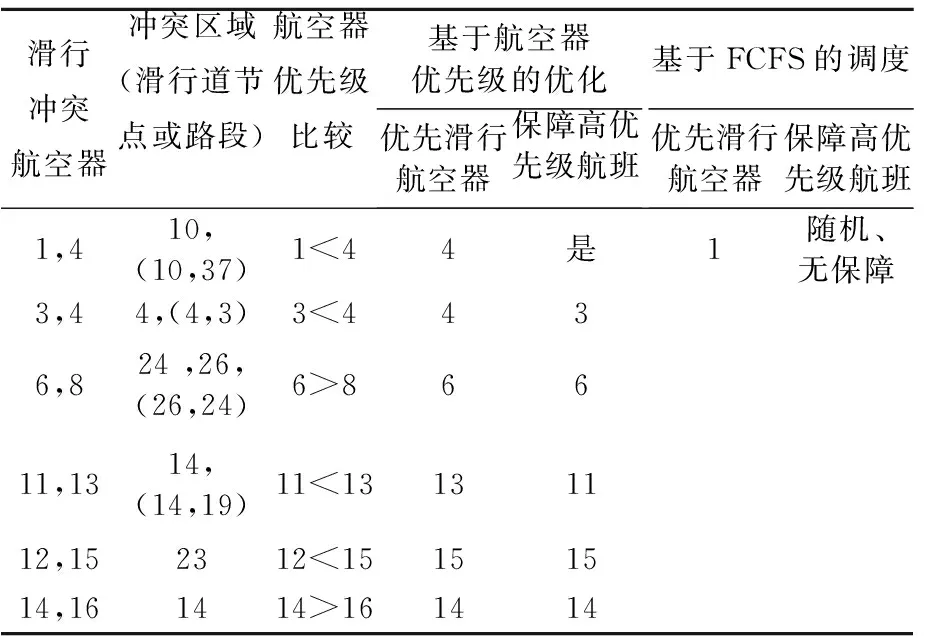
4.3 沖突解決策略過程分析
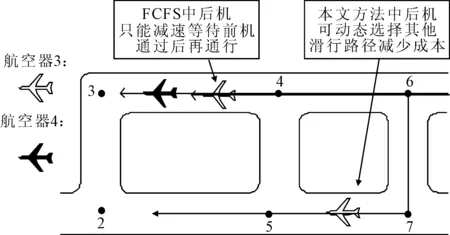

5 結 束 語

