支持向量雙效分類器及其應用
凌 萍,榮祥勝,李 雪
1(江蘇師范大學 計算機科學與技術學院,江蘇 徐州 221116)2(空軍勤務學院 訓練部,江蘇 徐州 221000)3(澳大利亞昆士蘭大學 信息技術學院,澳大利亞 布里斯班 4067)
1 引 言
分類是人類認知未知事物的基礎方法之一,也是機器學習領域的重要研究問題之一.在眾多分類方法中,以支持向量機(Support vector Machine,SVM)[2]為代表的基于支持向量的分類方法以扎實的理論基礎和良好的實驗表現成為研究熱點,得到了廣泛的應用,其變體分類器不斷涌現.根據分類模型的不同,可將基于支持向量技術的分類器分為兩組:基于超平面的分類器,和基于超球體的分類器.前者在兩類之間構造超平面,以分離兩類,如GEPSVM[3],MVSVM[4],TWSVM[5],PTSVM[6].后者為各類構造覆蓋類內成員的超球體,以獲知類別的輪廓,如TCSVDD[7],MCM-SVM[8],THSVM[9],pSVDD[10],NSVDD[11]等.這兩組分類器在理論及實踐中的作用舉足輕重,但隨著研究和應用的深入,兩組分類器的弊端也逐漸顯現.與此同時,也出現了一些通過生成超球體進行類別判斷的支持向量分類器,具體而言,基于超平面的分類器在處理含有重疊類別的數據集時,結果不盡人意.究其原因,在于此組分類器對類別之間間隔的過度依賴.倘若類別之間有重疊,則類間的間隔模糊,這給在保證類間間隔最大化的前提下生成優質分割面帶來困難,也必然影響最終分類結果.此后,雖有文獻提出了一些算法解決這一問題,但所給出的方法均未對支持向量模型本身做出改變,只是執行附加步驟或某簡單分類器,構成組合式分類器[12,13].這樣的改變往往增加了參數個數和算法運行成本.而且,改變之后的分類器仍是二分分類器.在解決多分類問題時,需要作為基本分類器提供局部決策結果,并根據某種集成策略匯總成為最終決策.
另一方面,對基于超球體的分類器而言,過適應是其難以避免的問題.因為此類方法源于用支持向量做數據描述的問題,其目標在于提供數據分布區逼真的輪廓描述.但,這種逼真的輪廓就分類而言,卻往往構成太過緊致的分類邊界.這造成,雖然分類器對訓練數據有較高的適應性,但對于未知的測試數據其適應能力相對較弱,推廣能力不足.
據此,本文提出一種新的雙效分類思想,在訓練分類模型的同時,學習類間的差異信息及類內的特征信息.從另一角度觀察,類間的差異信息是一種全局性信息,而類內的特征信息是一種局部性信息,將二者結合起來訓練分類模型,局部性信息將幫助全局性信息解決重疊區域的數據分類,而全局性信息將幫助局部性信息使其獲得更大的推廣能力.
進而,文中提出了收縮遠離球模型以實現雙效分類思想,并給出了支持向量雙效分類算法(Doubled-Informed classifier based on Support vectors,DISV).DISV為各類建立收縮遠離球,然后基于收縮遠離球信息來定義決策函數來完成分類.收縮遠離球的球面穿過類內的密集分布區,以獲知類內的特征信息,同時該球保持與其他類別的最遠距離,以達到最大的分類間隔并獲得豐富的差異信息.DISV輔以訓練數據抽取策略,和參數自適應調整策略,以降低算法代價.
文中將DISV應用于心臟肥大數據輔助診斷問題[15-17].長久以來,心臟肥大診斷問題上一直缺乏有效的計算機輔助診斷算法.原因是已有的心臟肥大訓練數據數量較少,且質量較差.加之在數據采集過程中產生的測量誤差,更為分類器的訓練增加了難度.SVM和神經網絡[18-20]是目前可解決心臟肥大診斷問題的兩種方法.其中SVM遵循結構風險最小化理論且可應對非線性及小樣本數據,因而更為常用.但正如前文所述,SVM在解決類別之間有重疊的數據集時,表現欠佳.而在當前環境下,患者數據和健康人數據之間的類別差異越發模糊,個體的生理信號值越發復雜多變,這給SVM在心臟肥大數據上的應用帶來困難.在此情形下,提出雙效分類思想及其實現算法解決上述困難,提高計算機輔助診斷的能力,具有實際的意義.
2 相關工作
最小包圍球是是本文收縮遠離球的理論基礎,因此對其做簡單介紹.給定數據集{x1…xN},其中xiRn.最小包圍球通過優化以下目標函數得到[14]:
(1)
s.t.‖Φ(xi)-a‖2≤R2+ξi,ξi≥0(i= 1…N)
Φ是從輸入空間到特征空間的非線性映射,ξi是松弛變量,a是球心,R是半徑,C是松弛變量的懲罰系數.引入核函數k(xi,xj)=<Φ(xi)·Φ(xj)>,得到最終優化目標為:
(2)
αi是拉格朗日乘子,滿足αi≠0的數據是支持向量.一般k為高斯核函數k(xi,xj)=exp(-‖xi-xj‖2/σ2),σ是尺度參數.
3 DISV算法細節
DISV是雙效分類思想的實現算法,它為各類構造收縮遠離球,并基于球的信息定義決策函數.為降低計算代價,DISV根據數據自身幾何性質對訓練數據進行抽取,并給出模型生成所需的平衡系數及鄰域尺寸的自適應設置策略.
3.1 收縮遠離球的初步模型
設數據集{x1…xN}覆蓋M個類,類別號記為:1,…,I,…M.將除I類之外的其他所有類的集合視為一個大類,其類別號記作nonI.則為I類構造的收縮遠離球通過優化如下目標函數完成:
minR2-η·∑xu∈nonI‖Φ(xu)-a‖2+C∑xi∈Iξi
(3)
s.t.‖Φ(xi)-a‖2=R2+ξi,ξi≥0 (xi∈I,xu∈nonI)
R,a,C及Φ的意義同前.xi取自I類,而xu取自nonI類.ξi是xi的松弛變量.在優化目標(3)中,‘R2’項與等式約束共同表達了“球面收縮”的要求,優化目標的第二項則使“球盡可能遠離其他類”.η是平衡系數,在“收縮”和“遠離”兩個優化要求之間做出權衡,一般地,取0<η<1.
3.2 決策函數定義
設I類的收縮遠離球的球心為a,半徑為R,Q是待分類數據,則Q關于I類的隸屬度函數定義為:
(4)
決策函數為:
L(Q)=maxJfJ(Q)
(5)
fI(Q)由Q和球心在特征空間內的內積決定,exp機制保證了值的穩定性.優化目標(3)涉及到I類和nonI類,即,全部的數據,因而計算代價較大.考慮到支持向量方法解的稀疏性,即,支持向量方法的解只由少數支持向量決定,這里將根據數據的幾何信息抽取出得對模型生成有重要作用的支持向量的候選者構成訓練子集.
3.3 數據抽取策略
對I類,生成兩個子集:SI和TI.SI收集了I類中位于密集分布區的數據,TI收集了I類邊界上的點,這些點將參與優化以保證球與其他類的最大分離.收縮遠離球將在SI和TnonI上訓練得到,并非在SI和TI之上.TnonI定義為除I類之外、其他類上所有TI子集的并集:
TnonI=∪{TJ|J=1,2…M∧J≠I}
(6)
′Λ′是合取邏輯操作.對I類,TnonI能夠包含其他類的全部邊界數據.因此,若為I類生成的球能與TnonI保持最大的遠離,則可認為該球與nonI類整體保持最大的遠離.
具體地,根據數據的鄰域信息生成SI.設I類大小為NI,定義I類上的臨近度矩陣H=(Hij)NI×NI:
(7)
i,j= 1,2…NI.Nei(xi)表示xi的鄰域.若兩個數據互為對方的鄰居,則它們的臨近度非零.定義選擇函數為:
(8)

為生成TI,需尋找邊界上的點.一般是通過計算數據點鄰域中異類鄰居的比例來判斷數據位置,但此方法在有些情形下失效.如圖1所示,當兩個占地較小類別彼此遠離,x0為 Class A邊界上的點,設x0的鄰域大小為r,即鄰域中鄰居的數目.只有當r增大到超過Class A的尺寸時,x0的鄰域才有可能覆蓋異到類數據.
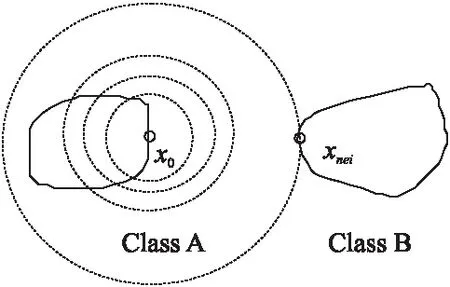
圖1 鄰域大小示意Fig.1 Illustration of neighborhood size
受[21]啟發,DISV通過觀察數據點的鄰居是否位于穿過該點的切平面的同一側來選出邊界點.如圖2,x1,x2和x3是三個邊界點,作出穿過三點與數據區相切的切平面.可知,對于x1和x3,兩個位于凸邊界的點,其鄰域中的全部鄰居均位于切線靠近數據區的一側;對于x2,位于凹邊界的點,其鄰域中的大多數鄰居位于切線靠近數據區的一側.

圖2 邊界點上的切平面 圖3 μi的近似計算示意

即對xi,求出其指向r個鄰居的向量:ρij=xj-xi,(j= 1…r).對ρij做標準化,記標準化結果為Eij,則μi近似計算為:
(9)
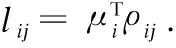
(10)
設定閾值λ,(0<λ<1),那么任何滿足Gi≥λ的xi入選TI.根據文獻[21],λ設為0.82.
3.4 收縮遠離球的改進模型
約簡訓練數據后,生成收縮遠離球的要求可改變為:球面需穿過SI中的數據,同時與TnonI中的數據保持最大的距離.下文設SI和TnonI大小分別為Z1和Z2,xi和xj來自SI,xu和xv來自TnonI,則收縮遠離球的新優化目標函數為:
(11)
s.t.‖Φ(xi)-a‖2=R2+ξi,ξi≥0 (i=1…Z1,u=1…Z2)
寫出(11)的拉格朗日函數:
(12)
求L對各變量的偏導數,得到:
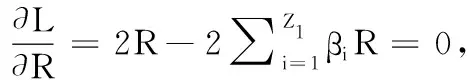
(13)

(14)

(15)
由于拉格朗日乘子γi>0,所以有0<βi (16) 由(14)計算(4)的分子: <Φ(Q),a>= (17) 設xsv為一支持向量,則(4)的分母計算為: R2=‖Φ(xsv)-a‖2 (18) 鄰域大小r過大,SI和TI會包含冗余數據;r過小,則造成信息丟失.DISV根據I類內的局部信息對r進行個性化的設置,即每個類都有其特定的r.具體地,在I類內,計算距離矩陣:D= (dij)NI×NI.升序排列D的各行.隨后,在各行上尋找產生最大間隔的位置:記gap(i)= maxj{dij-di,j-1},(i= 1…NI,j= 2…NI).最后,設定I類上的鄰域尺寸為:r= average {gap(i)},(i= 1…NI). 目標函數(11)中,η是收縮遠離球的收縮程度與遠離程度之間的權衡系數.本文中,將根據類別大小為每一類設定因地制宜的η.對I類,仍記其訓練子集SI和TnonI的大小為Z1和Z2,具體分析如下. 當Z1 首先使用二維人工數據集實驗,其包含兩個重疊類,如圖4所示.將DISV與基于超平面的分類器進行比較:SVM,MVSVM[4],TWSVM[5]和PTSVM[6].圖5至圖9依次給出了五個分類器的結果.可見,各分類器在非重疊區域上均可做出正確決策.但在類間重疊區上,DISV有11個分類錯誤,SVM有25個分類錯誤,MVSVM、TWSVM及PTSVM各有26、19和17個分類錯誤.這說明雙效分類思想有效,可幫助分類器獲得類內的特征信息和類間的差異信息,以增強分類器的類屬鑒別能力,從而在間隔數據上取得更高的分類準確率. 圖4 數據集 圖5 DISV分類結果 圖6 SVM分類結果 圖7 MVSVM分類結果 圖8 TWSVM分類結果 圖9 PTSVM分類結果 接著,在UCI[22]數據集上觀察DISV與TCSVDD[7],MCM-SVM[8],THSVM[9],pSVDD[10],NSVDDv[11].由于pSVDD,TCSVDD與THSVM均為二分分類器,這里只選用二類數據集以避免集成策略等外在因素對分類器自身性能的影響.表1和表2記錄了訓練集和測試集上的分類準確率,其中”Traning Ratio”一列表示從數據中隨機抽取的訓練數據的比例,黑體表示最優結果. 表1 訓練數據上的分類準確率(%)Table 1 Classification accuracy on training data (%) 表2 測試數據上的分類準確率(%)Table 2 Classification accuracy on testing data (%) 從表1中可得出如下結論: 1)除DISV外,6個超球體分類器在訓練集上表現優異.這是由于它們的優化目標的本質目的是建立訓練數據的描述,生成緊致的數據輪廓.為此,分類器會收集數據內部盡可能多的特征,以全面掌握訓練數據的信息,因此它們能夠對訓練數據做出準確的類別判斷. 2)DISV在訓練集上的表現遜于超球分類器,但與最優結果的差距較小. 3)當訓練數據增多,各個分類器的訓練準確率都有所提高. 從表2可得如下結論: 1)DISV的測試準確率高于6個超球分類器.這說明相對于基于超球體的分類器,DISV有更高的推廣能力.這也說明雙效分類思想有效,可以避免出現過適應問題. 2)當訓練數據較少時,DISV在測試集上相對于超球體分類器的優勢更為明顯.這是因為,基于超球的分類器僅僅依賴于學習類內的數據特征,當訓練數據量少,得到的分類器的類屬判斷能力會有所下降.而DISV并不完全依賴于類內數據信息,小規模訓練數據對DISV的影響并不明顯,所以DISV表現良好. 3)當訓練數據增多,所有分類器的測試分類準確率均提高. 繼續使用UCI上的多類數據集進行實驗,觀察DISV與超平面分類器和超球體分類器的表現.對其中的二分分類器,采用OVO和OVA方式[23,24]將其集成,最終決策由投票機制確定.隨機抽取20%的數據作為訓練數據,其他數據作為測試數據.設PTSVM的映射方向數為1. 表3記錄了10次獨立實驗中測試集上分類準確率的平均值及方差.可知,DISV在10個數據集中的6個上取得了較好的結果,在其余4個數據集上給出了與最優結果非常接近的結果.這說明了雙效分類思想的有效性.由于GEPSVM、MVSVM、TWSVM和PTSVM生成了穿過數據的超平面,MSM-SVM,TCSVDD,和THSVDD生成了包圍球,所以表3也說明,收縮遠離球描述類內特征的能力強于超平面和包圍球,其學習獲得的類間差異信息確實幫助DISV擁有更強的分類能力.就7個二分分類器而言,大多數情形下,OVO方式優于OVA方式.這表明,集成方式確對二分分類器其在解決多分類問題時的結果有影響.注意到TWSVM在Thyroid和Flag上的OVA結果優于其OVO結果,MVSVM在Vowel上,以及pSVDD在Lung Cancer上也有類似情況,如表3中′*′所示.可見,當二分類分類器被用于解決多分類問題時,分類結果不僅與集成方式有關,也與數據本身密切相關. 表3 多類數據集上的測試準確率(%)Table 3 Testing classification accuracy on multi-class datasets (%) 5個超球分類器中,MCM-SVM的表現更好,但它的分類準確率仍低于DISV,原因在于兩個方面.一是前者使用了包圍球,后者使用收縮球.在描述數據內部特征時,后者能力更強.二是前者是通過令球面與其他類中的最近數據點的距離達到最大,來實現球與其他類數據的遠離.這種做法非常易于受到孤立點及錯誤分布點的影響,導致超球體未能實現與其他類最大程度的遠離.注意到在表2給出的二分數據集上的實驗結果中,MCM-SVM的表現還不及THSVM,而在表3中,其表現已超過THSVM.這說明,THSVM作為二分分類器,解決二分問題時具有優勢,而在解決多分問題時,受多個外部因素的影響,其最終分類能力有所降低. 實驗使用MGH/MF和Fantasia數據集[26-28],使用WFDB軟件[29]和Cygwin系統[30]對兩數據集數據進行觀察和處理.MGH/MF和Fantasia數據集分別包含了250個患者及40個健康人的心電記錄.其中每個心電記錄包含了三個文件:注釋文件、心電數據文件和病史文件.實驗主要對心電數據文件中的心電波形進行分析處理.視兩次R波之間的波形為一次心跳,并在一個心電記錄中,選擇5次心跳描述該心電信息.由于一次心跳的波形由幾百個采樣點組成,這里選擇50個采樣點描述一次心跳過程,即,一次心跳由一個50維的心電向量進行描述.而一個心電記錄由5個50維的心電向量進行描述.實驗時,將向量中的各分量減去相應維上的平均值來做數據標準化. 訓練數據抽取方案為:i){15,25};ii){15,35} ii){15,40};a){35,20};b){50,20};c){65,20};1){30,32};2){35,32}.大括號中的兩個數表示分別從MGH/MF和Fantasia數據集中隨機選擇出的患者記錄和健康人記錄的數目,它們對應的心電向量將構成8個訓練集,其他記錄對應的心電向量則組成測試集.這8個訓練集覆蓋了三種情形:病人數據量小于、大于以及接近于健康人數據量. 為觀察DISV的隸屬度函數的質量,首先定義一個評價矩陣.設數據集{x1…xN}覆蓋了M個類,該數據集上的個隸屬度函數記為:f1,f2,…,fM.則對xi(i=1…N)關于fI的隸屬度fI(xi)的評價定義為: (19) 其中label(xi)表示xi真正的類別號.整個數據集上的評價結果構成矩陣:W=(WiI)N×M.一般地,較小的WiI表示fI能夠較好地表示xi在I類上的隸屬程度.此時包含了兩種情形.一是I恰為xi的真正類別號,此時WiI越小,fI(xi)越大,那么fI(xi)對“xi屬于I類”這一決策的表達越強烈.二是I非xi的真正類別號,此時WiI越小,則fI(xi)越小,它對“xi屬于I類”這一決策的表達則非常微弱.因此矩陣W可全面評價M個隸屬度函數在數據集上的決策質量.進一步地,在W之上給出如下的測度,以期用一個標量表示隸屬度函數的質量: (20) 顯然,CE越小,隸屬度質量越好. 本文設定NN為三層網絡結構,各層的神經元數目分別為50,5/7/9/11和1.其中,隱層的神經元數目分別為5、7、9和11來生成四個不同的NN分類器,記作:NN1,NN2,NN3及NN4.它們的最大迭代次數設為104.各層的轉移函數分別為g1(x)=x,g2(x)=2/(1+exp(-2x))+1和g3(x)=x.注意,四個神經網絡分類器在訓練過程中,以1和-1作為病人記錄和健康人記錄的理想輸出值.這里基于輸出層的結果g3(x),定義它們的隸屬度函數為: (21) (22) 表4 軟分類結果的CE值Table 4 CE values on soft decisions of classifiers 表4給出了各分類器的CE值.其中,MCM-SVM的軟分類結果由文獻[25]中的方法提供.由表4可知,在心臟肥大疾病診斷問題上,DISV的表現優于4個NN分類器和MCM-SVM.這說明,雙效分類思想是有效的,它能夠幫助DISV在訓練分類器過程中同時收集類內的個性化特征信息和類間差異信息,進而得到具有更強的類屬鑒別能力的分類器.實驗中MCM-SVM的軟分類結果質量好于四個NN分類器,這歸功于支持向量技術在解決小樣本、非線性問題上相對于神經網絡方法的優勢.從NN1到NN3,隱層神經元的數目減增,隸屬度函數的質量也漸漸提高.但神經元數目并非越多越好.從NN3到NN4,雖然神經元數目增加,但隸屬度的評估值并未減低反而增加,即,隸屬度函數的質量有所降低.這說明,對本文實驗中涉及到的心臟肥大實驗數據而言,9個神經元是隱層神經元的最佳數目. 最后,觀察DISV的硬分類結果.除了已經涉及到的分類器,這里還運行了LDSVM[31].LDSVM是基于SVM的一個集成分類器,由SVM和KNN組成.SVM在測試數據到達之前訓練完成,當測試數據到達后,若SVM給出的決策結果的信心指數低于指定的閾值,則啟動kNN,對初始決策進行修正.這里仍根據表4的方案生成8個訓練數據集,其他數據作為測試數據.以分類正確率作為評價標準.表5給出了各分類器在10次獨立實驗的平均正確率和方差. 心臟肥大數據集中的數據的分布更復雜,類別之間的差異更模糊.在這樣的數據上,DISV給出了優于同類分類器的表現,這再一次驗證了雙效分類思想的有效性和DISV可以克服類別之間有重疊及過適應問題的能力.其他各分類器的表現與前文進行二分時的實驗結果類似,不再贅述,這里只觀察LDSVM的分類結果.LDSVM的表現優于NN3,SVM,TCSVDD,pSVDD和NSVDDv,但次于其他三個分類器.深入分析LDSVM的SVM和kNN均是對間隔較為敏感的分類器.正如前文所述,心臟肥大數據的類間間隔模糊且復雜,即類間間隔內的數據會較其他數據集更多,這造成SVM給出更多的不佳決策需kNN修正.而kNN是根據基于SVM分界面函數定義的測度定義計算數據之間的距離,然后依據近鄰原則給出決策.此時分類雙方的重疊情況,使得SVM的分界面函數質量欠佳,當然由此定義的測度也受影響,從而令kNN的決策質量下降. DISV的時間耗費主要集中在三個方面.一是在設定鄰域大小時,對數據的排序.若使用快速排序算法,則時間復雜度為O(Nc·log(Nc)),其中Nc是各類的平均大小.二是在求各點的切平面時在鄰域里計算法向量,其復雜度為O(Nc·r).第三部分時間耗費在生成收縮遠離球的二次優化過程上,為O((Z1+Z2)3),其中Z1和Z2是SI及TnonI的大小. 表6列出了相關分類器在二分及多分任務下的時間復雜度.其中′-′表示NN的訓練過程涉及多種因素,其時間復雜度難以用顯式的式子表達. 表5 DISV和同類算法的正確率比較 (%)Table 5 Comparison of accuracy of DISV with the peers 從表6中可得如下結論. 1)TCSVDD和MCM-SVM在二分任務下的時間耗費一致. 2)SVM和LDSVM在二分任務下的時間耗費一致,他們需要分類雙方數據的參與生成間隔內的一個超平面. 3)多分任務下,SVM,LDSVM,TCSVDD的時間耗費一致. 4)表6雖不可給出確定性結論,但DISV是在訓練子集上完成二次優化,其他分類器均在數據全集上進行優化,因此可通過設置訓練子集的大小間接控制DISV的時間耗費,在算法運行代價上比同類算法有一定的靈活性. 表6 時間復雜度分析Table 6 Analysis of time complexity 本文提出了雙效分類思想,該思想在訓練分類器過程中同時學習類間差異信息和類內特征信息,從而克服基于超球體和基于超平面的分類思想遇到的過適應及難于解決重疊類別的問題.文中給出了雙效分類思想的實現算法DISV,DISV為每一類構造收縮遠離球,并基于此定義決策函數.收縮遠離球與其他類保持最大程度的遠離,且球面穿過類內密集分布區.為提高算法效率,根據數據的幾何信息對訓練數據進行約簡,平衡系數及鄰域尺寸也進行了自適應的設定.實驗驗證了雙效分類思想的有效性,而且將DISV應用于心臟肥大數據,進行計算機輔助診斷,其表現優于同類算法. : [1] Vapnik V.Statistical learning theory[M].New York:Wiley Press,1998. [2] Vladimir C,Ma Y Q.Another look at statistical learning theory and regularization[J].Neural Networks,2009,12(7):958-969. [3] Mangasarian O,Wild E.Multisurface proximal support vector classification via generalize eigenvalues[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(1):69-74. [4] Ye Q,Zhao C,Ye N,et al.Multi-weight vector projection support vector machines[J].Pattern Recognition Letters,2010,31(13):2006-2011. [5] Khemchandani R,Chandra S.Twin support vector machines (TWSVM)for classification[M].Twin Support Vector Machines,Berlin:Springer,2017:43-62. [6] Chen X,Yang J,Ye Q,et al.Recursive projection twin support vector machine via within-class variance minimization[J].Pattern Recognition,2011,44(10):2643-2655. [7] Huang G,Chen H,Zhou Z,et al.Two-class support vector data description[J].Pattern Recognition,2011,44(2):320-329. [8] Hao P Y,Chiang J H,Lin Y H.A new maximal-margin spherical-structured multi-class support vector machine[J].Applied Intelligence,2009,30(2):98-111. [9] Peng X,Xu D.A twin-hypersphere support vector machine classifier and the fast learning algorithm[J].Information Sciences,2013,221:12-27. [10] Nguyen P,Tran D,Huang X,et al.Parallel support vector data description[C].Proceedings of International Conference on Artificial Neural Networks,2013:280-290. [11] Mu T,Nandi A K.Multiclass classification based on extended support vector data description[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),2009,39(5):1206-1216. [12] Zhou H,Wang J,Wu J,et al.Application of the hybrid SVM-KNN model for credit scoring[C].Proceedings of 9th International Conference on Computational Intelligence and Security,IEEE,2013:174-177. [13] Nayak R K,Mishra D,Rath A K.A Na?ve SVM-KNN based stock market trend reversal analysis for Indian benchmark indices[J].Applied Soft Computing,2015,35:670-680. [14] Tax D M J,Duin R P W.Support vector data description[J].Machine Learning,2004,54(1):45-66. [15] Shiraishi J,Li Q,Appelbaum D,et al.Computer-aided diagnosis and artificial intelligence in clinical imaging[J].Seminars in Nuclear Medicine,WB Saunders,2011,41(6):449-462. [16] El-Baz A,Beache G M,Gimel′farb G,et al.Computer-aided diagnosis systems for lung cancer:challenges and methodologies[J].International Journal of Biomedical Imaging,2013:1-46. [17] Chang W Y,Huang A,Yang C Y,et al.Computer-aided diagnosis of skin lesions using conventional digital photography:a reliability and feasibility study[J].PloS one,2013,8(11):e76212. [18] Anthony M,Bartlett P L.Neural network learning:Theoretical foundations[M].Cambridge University Press,2009. [19] Demuth H B,Beale M H,De Jess O,et al.Neural network design[M].Martin Hagan,2014. [20] Neural network models of conditioning and action[M].Routledge,2016. [21] Li Y.Selecting training points for one-class support vector machines[J].Pattern Recognition Letters,2011,32(11):1517-1522. [22] Arthur Asuncion,David Newman.UCI machine learning repository[EB/OL].http://archive.ics.uci.edu/ml/, 2017.5 [23] Galar M,Fernández A,Barrenechea E,et al.An overview of ensemble methods for binary classifiers in multi-class problems:Experimental study on one-vs-one and one-vs-all schemes[J].Pattern Recognition,2011,44(8):1761-1776. [24] Murino V,Bicego M,Rossi I A.Statistical classification of raw textile defects[C].Proceedings of the 17th International Conference on.IEEE,2004,4:311-314. [25] Hao P Y.A new fuzzy maximal-margin spherical-structured multi-class support vector machine[C].Proceedings of IEEE International Conference on Machine Learning and Cybernetics (ICMLC),2013,1:241-246. [26] Welch J,Ford P,Teplick R,et al.The massachusetts general hospital-marquette foundation hemodynamic and electrocardiographic database-comprehensive collection of critical care waveforms[J].Clinical Monitoring,1991,7(1):96-97. [27] Goldberger A L.Components of a new research resource for complex Physiologic signals,PhysioBank,PhysioToolkit,and PhysioNet,American heart association journals[J].Circulation,2000,101(23):1-9. [28] Iyengar N,Peng C K,Morin R,et al.Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics[J].American Journal of Physiology-Regulatory,Integrative and Comparative Physiology,1996,271(4):1078-1084. [29] Moody G B.WFDB applications guide[J].Harvard-mit Division of Health Sciences and Technology,2003,10:30-31. [30] Vinschen C,Faylor C,Delorie D,et al.Cygwin user′s guide[M].Red Hat,1998. [31] Ling P,Gao D,Zhou X,et al.Improve the diagnosis of atrial hypertrophy with the local discriminative support vector machine[J].Bio-Medical Materials and Engineering,2015,26(s1):1813-1820.4 參數自適應設置策略
5 實驗分析
5.1 雙效分類思想有效性測試
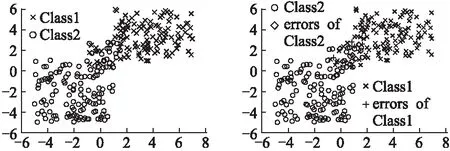

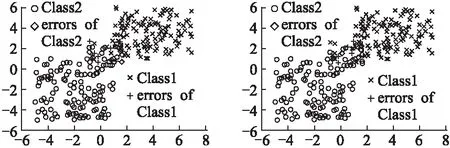
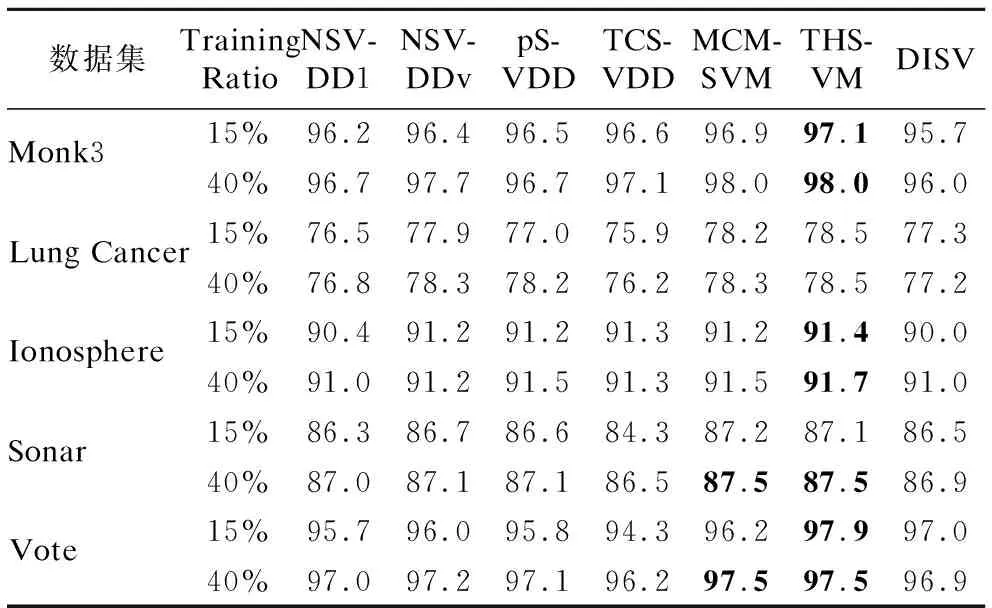
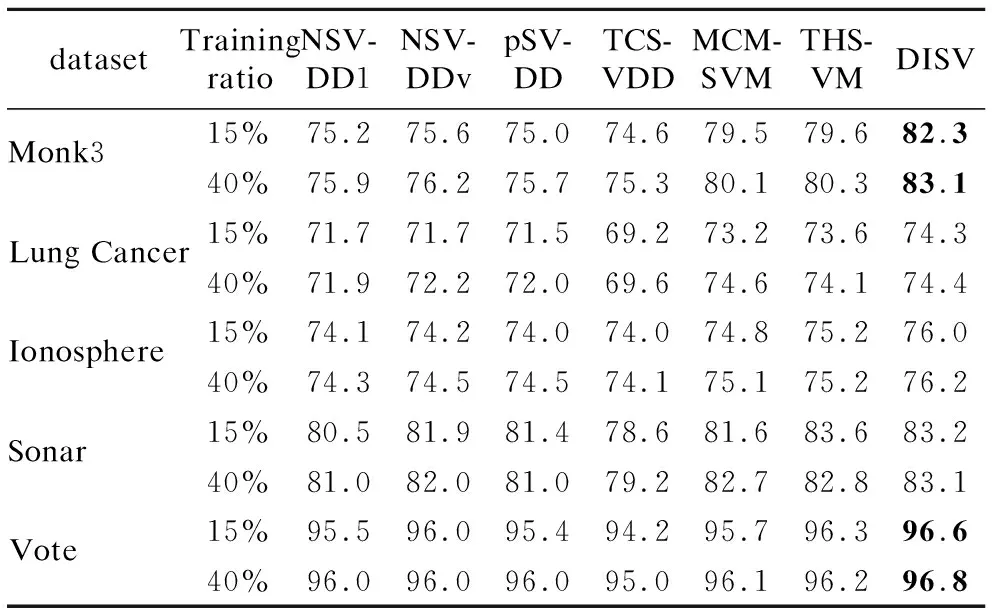
5.2 基準數據集上的實驗分析

5.3 在心臟肥大數據上的應用

5.4 復雜度分析


6 結 論

