在線密度敏感哈希算法研究

王 星,于江旭,唐曉亮,閆慧斌

1(遼寧工程技術大學 電子與信息工程學院,遼寧 葫蘆島 125105)2(遼寧工程技術大學 研究生院,遼寧 阜新 123000)3(遼寧工程技術大學 軟件學院,遼寧 葫蘆島 125105)

1 引 言

隨著網絡設備和信息技術的飛速發展,數據在社會生活的方方面面起著越來越重要的作用,如何更快更準確地對大規模數據進行處理一直是人們的研究熱點,近鄰搜索[1]是最常見的數據處理方式之一.近鄰搜索算法可以分為精確最近鄰搜索[2,3]和近似最近鄰ANNs[4](Approximate Nearest Neighbors)搜索.k最近鄰[5]是比較經典的精確近鄰搜索算法,許多精確近鄰搜索算法都是基于樹結構(比如說KD樹[6],R樹[7]等)的近鄰搜索,但是在高維數據的檢索中,這些算法效率會直線下降,因此近似最近鄰搜索的研究得到了人們的關注,越來越多基于哈希的ANNs算法[8,9]被提了出來.ANNs的特點是在損失少量精度的條件下實現快速的近鄰搜索,提高效率的同時也可以得到精度相對較高的搜索結果.基于哈希的方法是ANN搜索的代表之一.按照其產生哈希函數的原理,哈希算法大致可以分為基于隨機映射的哈希算法和基于學習的哈希算法.前者不考慮數據分布[8],而后者根據數據分布形成哈希函數[9].

上述的精確最近鄰搜索算法和基于哈希的搜索算法都是基于靜態數據的搜索算法,其處理數據的量總體上是不變的.但在實際應用中,遇到動態的數據,或者數據量比較大,無法一次性放入內存時,這些算法就無法使用.比如在數據庫中進行數據搜索,當有新的數據加入數據庫時重新對數據進行一次近鄰搜索是不現實的,浪費大量的時間和內存,于是許多處理動態數據的技術[10,11]被提了出來.在線k均值聚類算法[11]可以在保持原來數據樣本不變的情況下對新的數據樣本進行快速聚類.

針對現階段的哈希算法無法有效處理大規模動態數據的問題,本文提出一種新的在線k均值聚類算法,并將其與密度敏感哈希算法[12]結合,形成一種基于在線學習[13]的哈希算法,即在線密度敏感哈希ODSH (Online Density Sensitive Hash),該算法首先使用在線k均值聚類對數據進行預處理量化,然后根據產生的量化結果生成動態的超平面,根據超平面求出哈希方程,求出對應的投影向量和截距,最后使用投影向量對數據進行映射,得到哈希編碼,并使用漢明距離進行對比,獲得需要的近鄰結果.實驗證明,ODSH不僅具有基于學習哈希算法的特點,可以返回精確的結果,而且還可以快速地處理大規模動態數據.

2 相關工作

本節介紹哈希算法的基本概念和常見的哈希算法.

2.1 哈希算法的基本概念

哈希算法是一種可以將原始數據樣本快速映射到新的數據空間并生成二值編碼,可以實現高效數據檢索的搜索算法.各種哈希算法之間的主要區別在于采用了不同的哈希函數,根據哈希函數得到投影向量,再對數據進行映射獲取哈希編碼,哈希算法中最基本的哈希函數如公式(1)所示:

y=h(x)

(1)

h(·)是哈希函數,y是經過哈希函數映射后的哈希編碼,通常情況會使用多個哈希函數來組成一族哈希函數,產生多組哈希編碼,即,Y=[y1y2…ym]=[h1(x)h2(x)…hm(x)].哈希算法將任意長度的二進制值映射為較短的二進制值,廣泛地應用于快速檢索.基于映射的線性哈希搜索,第k個哈希函數定義如公式(2)[14]所示:

(2)

x是任意的一個數據點,wk是投影向量,tk是一個閾值,也可以稱為投影向量對應的截距,而f(·)表示的是一個目標函數.定義中的sgn函數只會返回{-1,1},經過哈希函數映射后的二進制編碼可以表示為bk=(1+Hk(x))/2.下面總結一下比較常見的哈希算法.

2.2 基于隨機映射的哈希

局部敏感哈希LSH[8](Locality Sensitive Hash)是最常用的哈希算法之一,它的基本思路是將原來空間中相鄰的數據點通過映射或者投影到新的數據空間中,其仍然相鄰的概率較大,而不相鄰的數據點映射到同一個數據空間的概率很小.LSH通過生成大量的隨機映射,生成較長的哈希表來保證數據檢索的準確率,其哈希函數比較簡單,容易實現,且速度較快,但是較長的哈希表會占用較大的內存,而較短的哈希編碼會導致檢索的準確率降低.

平移不變核哈希算法SKLSH[15](shift-invariant kernels Locality Sensitive Hash),平移不變核哈希算法利用了平移不變的核方法來產生隨機投影,原理近似于LSH.

2.3 基于學習的哈希

以上算法是非數據驅動的哈希算法,在哈希編碼長度較長的時候效果較好,但是有占用內存大,復雜度較高等限制,因此基于學習的數據驅動型哈希算法被提了出來.基于學習的哈希算法一般會通過分析數據點之間的關系和性質來指導哈希方程的產生,進而獲得投影向量對數據進行哈希映射,獲得需要的哈希編碼,主成分分析哈希算法PCAH[16](Principal Component Analysis Hash)通過主成分分析獲得數據的主要成分,將主要成分作為投影向量產生哈希編碼.

譜哈希算法SH[9](Spectral Hash)是比較常用的基于數據學習的哈希算法.它通過對原始數據集進行PCA降維獲得相似圖拉普拉斯矩陣的特征向量,然后對特征向量進行閾值化產生最后需要的二值編碼,譜哈希可以較好地提升檢索精度,但是譜哈希對多維數據的要求必須是均勻分布的,且不同維度上的哈希編碼相互獨立.

基于核的監督哈希KSH[17](Kernel-based Supervised Hash)使用帶標簽的數據進行學習得到哈希函數,將各數據再輸入到各哈希函數中得到數據對應的哈希編碼,實驗表明該基于核的監督哈希算法在度量距離和語義相似的搜索中表現出良好的性能.相比小規模的低維數據,大規模高維數據本身會存在某些結構特性,所以基于學習的數據驅動型哈希技術可以較好地實現數據(圖像,文本等)的快速檢索.本文提出的在線密度敏感哈希算法,可以有效地處理動態數據,并通過數據之間的密度特性來指導哈希函數的生成,可以有效地解決普通哈希方法無法對數據庫里中不斷增加的數據以及新抓取的網頁進行近鄰搜索的問題.

3 在線密度敏感哈希

本節將對ODSH算法分為三小節進行詳細闡述,首先給出在線k均值聚類算法的推導公式,然后描述投影向量的獲取過程,最后根據信息熵值對獲得的投影向量進行篩選.

3.1 在線k均值聚類

給出固定聚類個數的在線k均值聚類的調整公式:在某一段時間內,(t-1)和(t)表示時間的前后,N表示數據點的個數,K為固定好的分類結果組數.

(3)

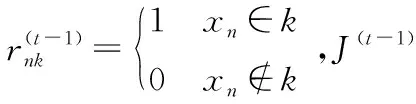
(4)

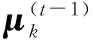
(5)

下面列出時間(t)下的在線k均值聚類的誤差平方和.

(6)

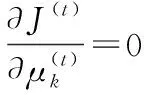
(7)

(8)

(9)

結合上式(7)(8)(9)可得公式(10)

(10)

公式(10)是在線更新的在線k均值聚類方程,通過它可以在不斷有新的數據點加入到原數據集的時候,快速而準確地獲得新的聚類結果.關于在線k均值聚類算法的組數k的確定將在實驗部分給出.

3.2 投影向量的獲取

經過在線k均值聚類獲得不同時間下的k個聚類結果,表示為{S1,S2…,Sk},(k的數已經固定),然后根據聚類結果來指導投影向量的產生.首先定義一下需要的變量,聚類結果將使用[12]中的n-最近鄰矩陣進行表示:

定義1.分類結果數據組的n最近鄰矩陣M

Nn(μj)代表了中心點μj的n個最近中心點集合,繼而得到n-相鄰組對的定義.

定義2.n-相鄰組對

當Mij=1的時候,組Si和組Sj為n-相鄰組對.

通過上一步得到的n-相鄰組對,下面通過這些相鄰組對來生成對應的投影向量,根據3.1得到的動態kmeans量化結果,對于相鄰組的表示點μi和μj,構建表示點的中垂面(假設三維空間,三維以上用超平面來表示)來對相鄰組進行切分.根根據文獻[12]的中垂面定義和公式(10)推導出動態超平面公式,見公式(11),公式等號左面的公式表示的是時間(t)下的超平面,等號右邊為時間(t-1)下的超平面表示公式.

(11)

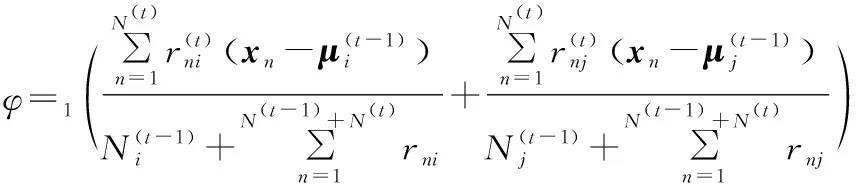
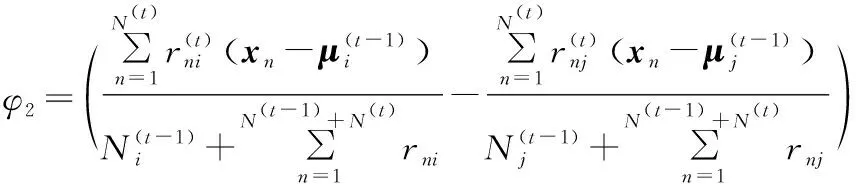
(12)

再根據超平面推得動態的哈希函數:

(13)

w(t)=w(t-1)+φ2

(14)

(15)

3.3 投影向量的篩選

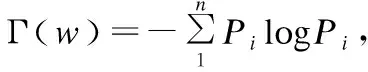
4 實驗結果

4.1 數據集

該實驗使用以下三個公用數據集:

?Sift_128d數據集:該數據集是從ANN_SIFT1M中截取出來的,因受設備的限制,只使用其中的60000個sift特征,每個特征128維度.

?Gist_320d_CIFAR-10:CIFAR-10數據集是從Alex Krizhevsky等人收集的8千萬小圖片數據集中取到的子數據集,該數據集包含了60000個彩色圖片的gist特征,維度為320維,數據集以及實驗中對比的哈希算法相關代碼可以在*https://github.com/willard-yuan/hashing-baseline-for-image-retrieval處下載.

?Gist_960d:該數據集從ANN_GIST1M中截取,同樣含有60000個sift特征,維度為960維.ANN_SIFT1M和ANN_GIST1M可在*http://corpus-texmex.irisa.fr/處下載.

4.2 實驗中對比的哈希算法

局部敏感哈希算法LSH[8]是通過生成大量的隨機映射來生成哈希編碼的哈希算法.

平移不變核哈希算法SKLSH[15](shift-invariant kernels Locality Sensitive Hash),它是LSH的一種改進算法.

主成分分析哈希算法PCAH[16]通過主成分分析來獲得數據主要成分來指導投影向量的產生.

譜哈希SH[9],該算法基于上述的PCA哈希算法,對PCA后的特征向量進行閾值化產生最后需要的二值哈希編碼.

主成分分析-隨機旋轉矩陣哈希算法[18]PCA-RR(Principal Component Analysis- Random Rotation),該算法在PCAH算法的基礎上融入隨機旋轉矩陣,相比PCAH算法性能有較大提升.

在線密度敏感哈希算法ODSH(Online Density Sensitive Hash),這是本文提出的哈希算法.

4.3 實驗設計與分析

首先對實驗參數進行設置,哈希編碼的位數l設置為ln=8,16,32,64,128位編碼,通過不同的哈希編碼位數來測試哈希算法的性能.

本文的在線k均值聚類算法需要預先固定好聚類的個數,k的值由哈希編碼的位數決定,因為哈希編碼的位數越大,需要的投影向量就越多,對應的超平面也越多,所以需要的數據組的個數也越多,所以組數k的個數與哈希編碼的位數有關,故設置一個參數A來確定組數k,令k=A*ln,后續實驗中,通過固定哈希編碼的位數,以及固定的A和n-相鄰組對中的參數n,會發現當A=2,n=3的時候,在各位哈希編碼下在線密度敏感哈希算法的性能最好.下面會給出圖示和分析.

為了更好地與其他的哈希算法對比,本文使用同樣的數據集進行測試.針對本文提出的哈希算法,在程序中固定一部分數據集,然后通過迭代的方式將數據逐批次地導入到工作空間中,以此來實現數據的動態導入,根據每一批次數據導入后獲得的聚類結果構建超平面,訓練得到在線密度敏感哈希算法的哈希方程,求得投影向量和截距,最后獲得多組投影向量和截距.使用同樣的訓練數據集獲得其他哈希算法的哈希方程,通過投影向量獲得測試和訓練數據集對應的二值哈希編碼,計算訓練數據集與測試數據集之間的海明距離并排序,最后計算得到precision-recall值,以及平均準確率的平均值mAP(mean Average Precision),來衡量算法的性能.對本文提出的在線密度敏感哈希算法,根據多批次的結果計算得到多組precision-recall值和mAP值,取其平均值來與其他哈希算法進行對比.

4.3.1 參數選擇

實驗中使用mAP作為標準來進行參數的選擇,將哈希編碼長度設置為64位.首先將參數A固定,改變參數n的值來對本文的在線密度敏感哈希算法進行測試,并將數據可視化展現出來,然后再將參數n固定,改變參數A的值進行測試,結果如圖1、圖2所示.

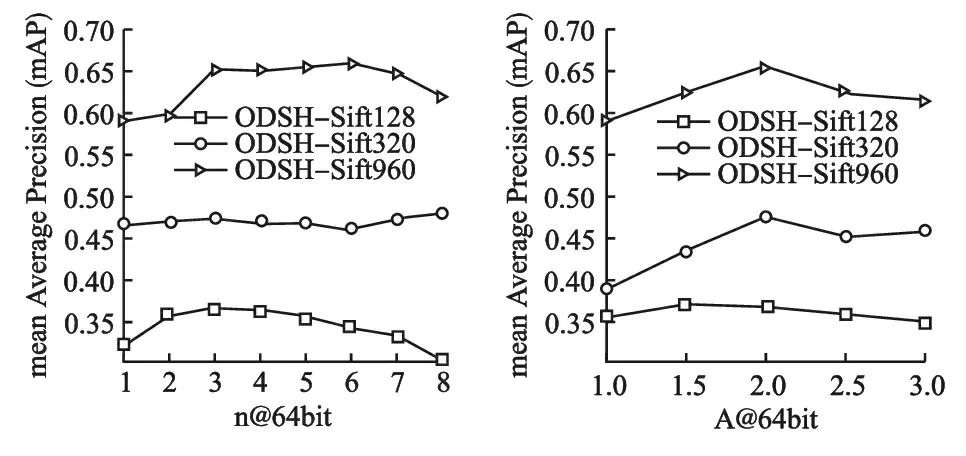
圖1 64位哈希編碼:不同參數n下的mAP 圖2 64位哈希編碼:不同參數A 下的mAP

如圖1所示,首先將參數A設置為2,固定不變,橫坐標n為選取的相鄰組參數,n從1到8取值,縱坐標為mAP的值.三條折線表示mAP在三個數據集下的變化.根據圖示可以看出隨著n-相鄰組的參數n取3到6時,mAP是比較理想的,考慮到n的取值不需要太大,算法里的超平面只需要切割比較近的數據簇,因此選n=3作為后續的實驗測試參數.

如圖2所示,這里將參數n設置為3,參數A從1到3取值,從圖2可以看出,三個數據集對應的三條折線,mAP的值在參數A=2時比較理想,在保證相對較高的準確度和較低的時間消耗情況下,選擇A=2作為實驗測試參數.

4.3.2 測試結果

圖3到圖5表示的是各哈希算法在三個數據集下,32位,64位,128位哈希編碼的precision-recall曲線圖,可以看出在不同維度的數據,不同位數的哈希編碼下,本文提出的在線密度敏感哈希均具有較好的性能.

圖6表示不同的哈希算法在三種數據集下,哈希編碼從8位到128位的平均準確率的平均值,SKLSH和LSH屬于非數據驅動型的哈希算法,可以看出他們在哈希編碼位數較少的情況下性能較差,但隨著哈希編碼位數的增加,其準確率增長幅度較大.基于數據驅動型的哈希算法如SH隨著哈希編碼位數的準確率增長幅度相比LSH等算法較小,特別是PCAH算法隨著哈希編碼的位數增長性能反而下降了,其原因是PCAH算法里的主成分分析得到的數據主成分分布比較集中,只能在有限位數的哈希編碼中起作用,隨著哈希編碼位數的增長,在后面的哈希編碼中識別最近鄰數據的性能會下降,PCA-RR算法引入了隨機旋轉矩陣,隨著哈希編碼位數的增加,平均準確率的增長比較明顯.分析本文提出的ODSH算法在三個不同維度的數據集中的表現可以發現,在線密度敏感哈希算法在不同編碼不同維度的性能都要好于上述哈希算法,也可以看出隨著維度的增加,其平均準確率的平均值會更高一些,可以看出在線密度敏感哈希算法同樣適合于高維數據的檢索.

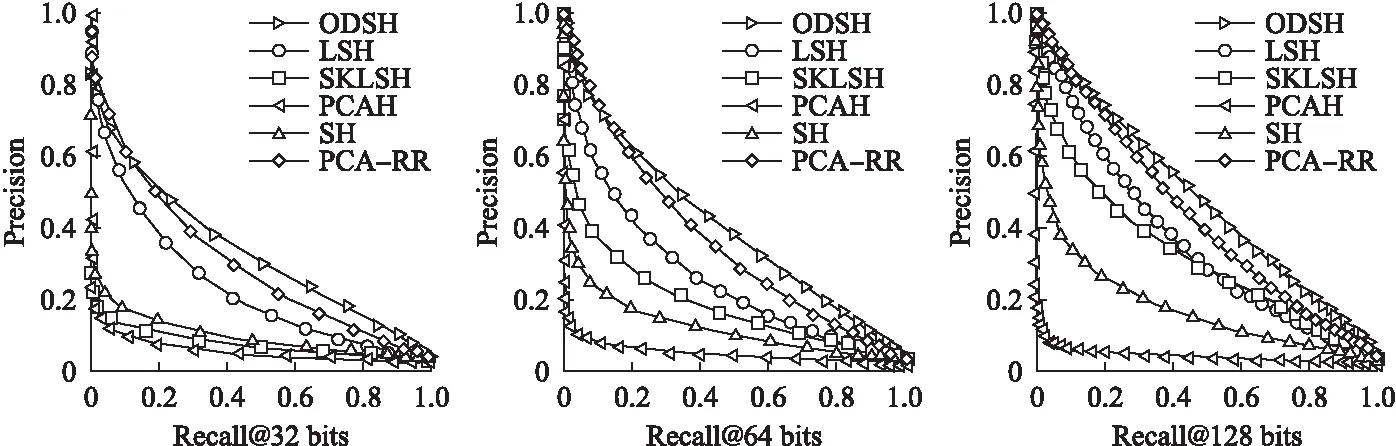
圖3 Sift _128維數據集Fig.3 Sift_128 dimension data set

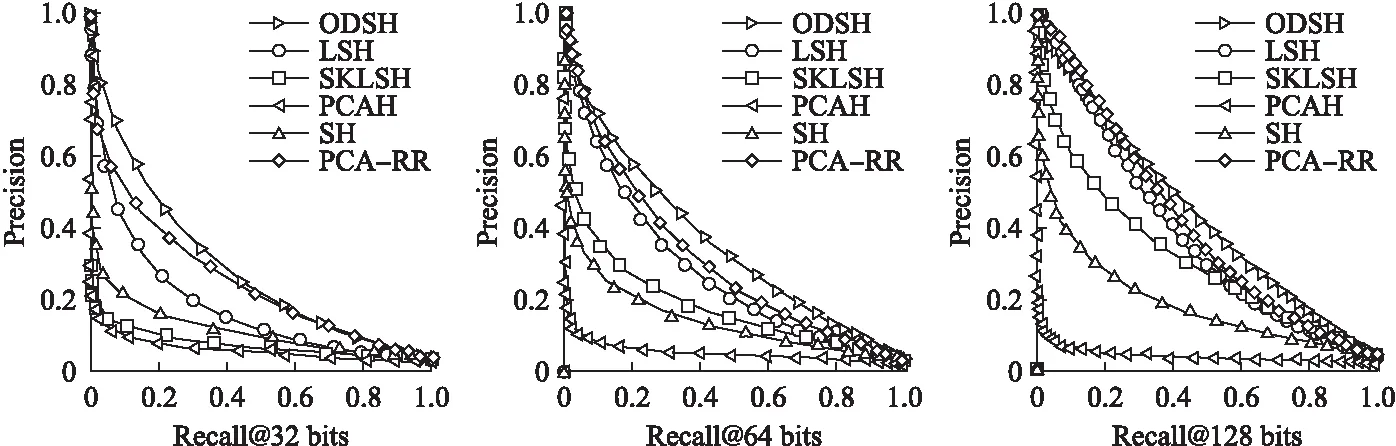
圖4 Gist _320維數據集Fig.4 Gist _320 dimension data set

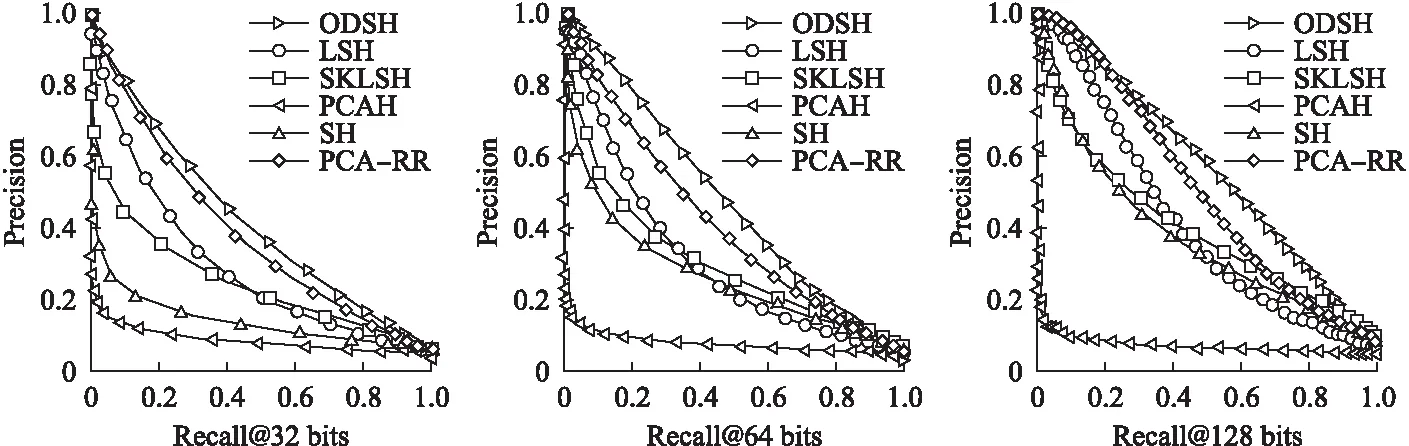
圖5 Gist_960維數據集Fig.5 Gist_960 dimension data set

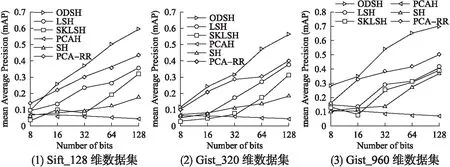
圖6 三種數據集下的平均準確率的平均值Fig.6 Average of the average accuracy of the three datasets

5 結論與未來工作

本文提出的基于在線k均值聚類的密度敏感哈希算法可以較好地應對動態數據搜索的情況,可以解決普通哈希算法無法解決的在線學習問題,通過大量的實驗對比,可以發現該算法具有較好的準確度和速度,但是該算法在超高維的數據下,比如說4096維度的數據下性能略低,故本文的下一步工作是對在線k均值聚類算法以及密度敏感哈希算法進行一系列參數優化,使其能更快速地對超高維數據進行處理,并在云平臺上測試算法性能.

：

[1] Brin S.Near neighbor search in large metric spaces [C].Proceedings of the 21th International Conference on Very Large Data Bases,1996:574-584.

[2] Dasgupta S,Sinha K.Randomized partition trees for nearest neighbor search [J].Algorithmica,2015,72(1):237-263.

[3] Tao Y F,Papadias D,Shen Q M.Continuous nearest neighbor search [C].Proceedings of the 28th International Conference on Very Large Data Bases,2002:287-298.

[4] Indyk P,Motwani R.Approximate nearest neighbors:towards removing the curse of dimensionality [C].Proceedings of the 30th Annual ACM Symposium on Theory of Computing,2000:604-613.

[5] Zhang Xu,He Xiang-nan,Jin Che-qing,et al.Processing K-nearest neighbors query over uncertain graphs [J].Journal of Computer Research and Development,2011,48(10):1871-1878.

[6] Friedman J H.An Algorithm for finding best matches in logarithmic expected time [J].ACM Transactions on Mathematical Software,1977,3(3):209-226.

[7] Guttman A.R-trees:a dynamic index structure for spatial searching [C].Proceedings of the 10th ACM SIGMOD International Conference on Management of Data,ACM,1984:47-57.

[8] Datar M,Immorlica N,Indyk P,et al.Locality-sensitive hashing scheme based on P-stable distributions [C].Proceedings of the 20th Annual Symposium on Computational Geometry,ACM,2004:253-262.

[9] Weiss Y,Torralba A,Fergus R.Spectral hashing [C].Proceedings of the 21th International Conference on Neural Information Processing Systems,2008:1753-1760.

[10] Li Song,Zhang Li-ping,Hao Zhong-xiao.Strong neighborhood pair query in dynamic dataset [J].Journal of Computer Research and Development,2015,52(3):749-759.

[11] Liberty E,Sriharsha R,Sviridenko M.An algorithm for online K-means clustering [J].Computer Science,2014:81-89.

[12] Jin Z,Li C,Lin Y,et al.Density sensitive hashing [J].IEEE Transactions on Cybernetics,2014,44(8):1362-1371.

[13] Mairal J,Bach F,Ponce J,et al.Online learning for matrix factorization and sparse coding[J].Journal of Machine Learning Research,2010,11(1):19-60.

[14] Wang J,Kumar S,Chang S.Sequential projection learning for hashing with compact codes [C].Proceedings of the 27th International Conference on Machine Learning,2010:1127-1134.

[15] Raginsky M,Lazebnik S.Locality-sensitive binary codes from shift-invariant kernels [C].Proceedings of the 22th International Conference on Neural Information Processing Systems,2009:1509-1517.

[16] Zhou X,Huang Z,Ng WWY.Weighted grid principal component analysis hashing [C].Proceedings of the 13th International Conference on Machine Learning and Cybernetics,2015:200-205.

[17] Liu W,Wang J,Ji R,et al.Supervised hashing with kernels [C].Proceedings of the 25th International Conference on Computer Vision and Pattern Recognition,2012:2074-2081.

[18] Gong Y,Lazebnik S,Gordo A,et al.Iterative quantization:a procrustean approach to learning binary codes [C].Proceedings of the 24th International Conference on Computer Vision and Pattern Recognition,2011:817-824.

附中文參考文獻：

[5] 張 旭,何向南,金澈清,等.面向不確定圖的k最近鄰查詢[J].計算機研究與發展,2011,48(10):1871-1878.

[10] 李 松,張麗平,郝忠孝.動態數據集環境下的強鄰近對查詢[J].計算機研究與發展,2015,52(3):749-759.