混合遺傳蝙蝠算法求解單目標柔性作業車間調度問題

徐 華,程 冰

(江南大學 物聯網工程學院,江蘇 無錫 214122)

1 引 言

車間調度問題一直以來都是科學研究的一個熱點.柔性作業車間問題(FJSP)是在作業車間調度的基礎上擴展的更加靈活復雜的調度問題.相比于經典的作業車間調度,FJSP考慮了同一個工藝可以在不同的機器上加工的問題,不同機器上的加工時間也有所不同.FJSP減少了對機器的約束,擴大了可行解的搜索范圍,增加了求解難度,使得調度問題更加復雜、更加靈活.柔性作業車間更加貼近實際生產中的制造環境,更符合現代柔性制造的理念.

首次提出FJSP的是Bucker P.和Schlie R.[1],此后便引起了廣大學者的關注研究.FJSP已經被證明是一個NP-hard問題[2].目前,求解FJSP的方法大多集中在智能算法以及多種智能算法結合的混合算法上,如遺傳算法(Genetic Algorithm,GA)[3-5]、蟻群算法(Ant Colony Optimization,ACO)[6,7]、粒子群算法(Particle Swarm Optimization,PSO)[8,9],還有一些其他的算法[10-13].蝙蝠算法(Bat Algorithm,BA)是一種模擬蝙蝠回聲定位機理得出的算法,是Yang在2010年提出的一種新興啟發式智能算法[14].發展至今,蝙蝠算法已經應用到很多領域,如函數優化[15]、無線傳感網絡[16,17]、電網系統[18,19]等.在生產調度領域,許多專家學者應用蝙蝠算法及其改進算法求解調度優化問題.夏晶晶等人提出一種改進型蝙蝠算法來優化車間內工件的最大完工時間[20].韓忠華等人提出基于漢明距離精英個體集的自適應蝙蝠算法求解柔性流水車間調度問題[21].Luo等人針對置換流水車間問題,將NEH算法與蝙蝠算法相結合,并將調度問題劃分為若干個子問題[22].Dao等人受并行處理的啟發,提出基于通信策略的并行蝙蝠算法來求解作業車間調度問題[23].

從上述內容中可以看出,蝙蝠算法成功的應用于車間調度領域,但是其相關性的研究尚不成熟,蝙蝠算法自身也有易陷入局部最優的缺點.本文結合遺傳算法的變異交叉操作,提出一種混合遺傳蝙蝠算法(HGBA)來求解單目標柔性作業車間問題.同時采用三種方式對種群進行初始化,在保證解的多樣性的同時也保證了解的質量;引用動態遞減的權重來均衡局部搜索與全局搜索;針對蝙蝠算法易陷入局部最優解的問題,提出一種基于變異操作的鄰域搜索;結合于本文采用的基于機器編碼方式,提出混合列交叉的策略來進行位置更新,避免產生無效解.最后通過實例測試,實驗結果證明了HGBA算法的有效性.

2 柔性作業車間調度模型

2.1 問題描述

柔性作業車間與經典作業車間的區別就是工序可在多臺機器上加工.根據工序可選加工機器集的大小,可將柔性作業車間調度分為兩類:一類是完全柔性作業車間調度(T-FJSP),即每個工序可以在所有的機器上加工;一類是部分柔性作業車間調度(P-FJSP),即至少有一個工序不能在所有的機器上加工.T-FJSP是P-FJSP的一種特殊情況,在實際情況中,P-FJSP中機器的選擇一般都存在約束,所以P-FJSP更具有實際意義,而且P-FJSP是比T-FJSP更復雜的調度問題.

FJSP可以簡單描述為:n個工件在m臺機器上加工,工件集J={J1,J2,…,Jn},機器集M={M1,M2,…,Mm}.每個工件Ji(i∈{1,2,…,n})有λi(λi≥1)道工序,并且每道工序可在一臺或者多臺機器上加工.每道工序可以任意選擇一臺機器加工,不同機器加工的時間長短也不同.調度問題的目標就是在滿足約束條件的基礎上,合理的安排工件的加工次序、加工時間以及加工機器.FJSP問題中的相關符號定義如下:

Oij表示工件Ji的第j(j∈{1,2,…,λi})道工序;

Wijk表示工序Oij在機器k上加工狀態,并且有:

(1)

Tijk表示工序Oij在機器k上的加工時間;

Bijk表示工序Oij在機器k上的開始加工時間;

Eijk表示工序Oij在機器k上的完工時間;

Ci表示工件Ji的完工時間.

本文的目標是使得最大完工時間Cmax最小,最大完工時間是指最后一個工件被加工完成的時間,代表著整個調度的生產周期.目標函數如下所示:

func=min(max(Ci)),1≤i≤n

(2)

2.2 約束條件

1)每個工序在加工過程中不允許被中斷,假設機器無故障:

Eijk=Bijk+Tijk

(3)

2)每個工件必須按照工序的順序加工,不可亂序,即Oij完成之后才可加工Oi(j+1):

(4)

也可表示為:

(5)

3)不同工件的工序之間不存在先后約束.

4)同一個機器在某時刻只允許加工一道工序;即當工序Oij在時刻t(t>0),若有Wijk=1,則當i≠p且j≠q時,必不存在Opq使得Wpqk=1.

5)每臺機器相互獨立,任何一臺機器是否工作、是否故障都不影響其他設備,并且所有機器在開始時刻(t=0)均可以開始工作.

表1給出3個工件、5個機器(3×5)的P-FJSP調度例子,表中的數據表示工序在對應的機器上的加工時間,其中“—”表示工件不能在該機器上加工.

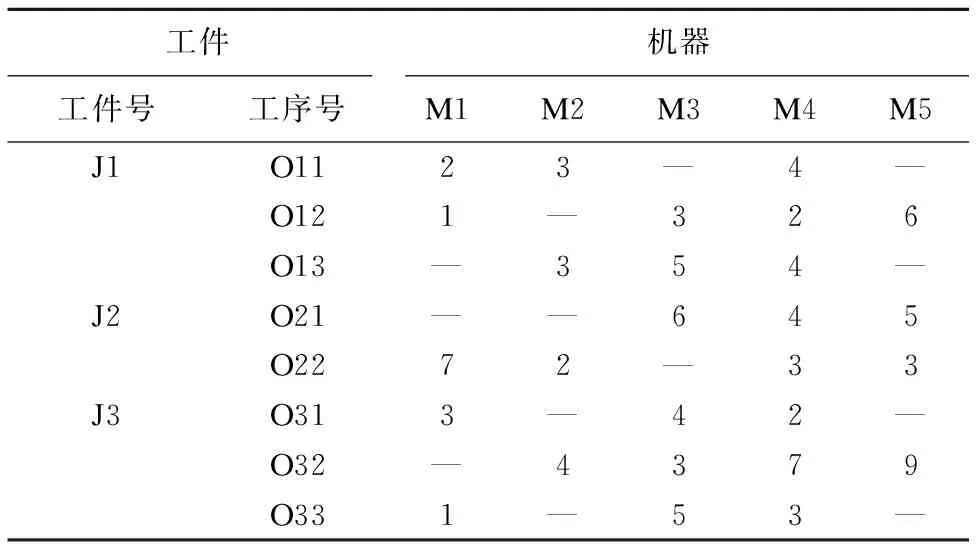
表1 3×5調度實例Table 1 3×5 Scheduling example

3 蝙蝠算法

蝙蝠算法是根據蝙蝠回聲定位的原理得出的啟發式算法.蝙蝠以速度vi在位置xi處隨機飛行,以頻率fi和響度A搜尋獵物.根據自身與獵物之間的距離來調節發射的脈沖頻率,調整發射的脈沖速率r0∈[0,1].在d維空間里,x=(x1,x2,…,xd)T,初始種群規模為pop_size,單個蝙蝠表示為xi(i=1,2,…,pop_size).蝙蝠算法相應變量更新如下:

1)速度與位置更新:

fi=fmin+(fmax-fmin)β

(6)

vi(t+1)=vi(t)+(xi(t)-x*)fi

(7)

xi(t+1)=xi(t)+vi(t+1)

(8)

其中,fi是發射頻率,取值范圍為[fmin,fmax];β為隨機變量,β∈[0,1];vi(t)、xi(t)為第t代蝙蝠的速度與位置,vi(t+1)、xi(t+1)為第t+1代蝙蝠的速度與位置,均為d維向量;x*表示當前的最優解;

2)局部搜索,對當前最優解按照如下規則進行搜索:

xnew=xold+εAt

(9)

xold表示選擇的一個解,xnew表示進行擾動后的新解;ε∈[-1,1],At表示第t代蝙蝠的平均響度.

3)響度與脈沖發射速度更新:

(10)

(11)

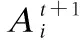
4 求解FJSP的遺傳蝙蝠算法

4.1 編碼方式

表2 可選機器集Table 2 Optional machine set

下面按照表一中給出的實例數據進行說明.從表中數據可知,工序O11可在M1、M2、M4這3個機器上加工,則有S1={1,2,4},可選機器個數SN1=3,對應的基因g1取值在[1,SN1]之間,假設此時取g1=3.同理,O12可以在M1、M3、M4、M5這4個機器上加工,則有S2={1,3,4,5},可選機器個數SN2=4,對應的基因g2取值在[1,SN2]之間,假設此時取g2=1.依照此方式可對基因序列進行完整的編碼.表2列出了工序的可選機器集.隨機給出一個完整的編碼序列為[3 1 3 3 4 2 1 2],通過編碼方式可以反向進行解碼,得出對應的工序的加工機器序列,因此上述編碼對應的工序加工機器為[4 1 4 5 5 3 2 3].圖1為解碼示意圖.

圖1 解碼示意圖Fig.1 Decoding diagram

4.2 種群初始化

許多智能算法如粒子群算法、遺傳算法等在某種程度上其性能易受初始種群的影響.在初始化種群的過程中既需要保證種群的多樣性,也需要保證種群的質量.因此,初始種群需要達到兩個基本要求:一是多樣性,多樣性好的初始解覆蓋的解空間大,搜索范圍廣,尋找到全局最優解的機率也更大;二是初始解的質量,解的質量影響著收斂速度.為了滿足這兩點,本文按照以下方案進行初始化.

1)隨機生成法:根據每個工序可選擇的加工機器,隨機選擇一臺機器.

2)最小時間選擇法:根據工序在可選機器上的加工時間選擇用時短的機器.當不同機器上的加工時間相同時,則比較機器上的現有的工作量(即機器上的處理時間),選取工作量小的機器.

3)第二小時間選擇法:選擇工序在可選機器上加工時間第二小的機器.

在初始化種群時,采用輪盤賭的形式.對于某一個解,其基因位上的值由如下方式決定:當rand<0.4的時候采用方案(1);當rand≥0.4,采用方案(2)選擇機器的,同時當工序可選的最小時間機器只有一個,為避免解的多樣性變差,則隨機選擇采用方案(2)與方案(3)來生成.

4.3 慣性權重重定義

為了平衡局部搜索與全局搜索,針對公式(7)引入權重變量變為:

vi(t+1)=w*vi(t)+(xi(t)-x*)fi

(12)

并且采用慣性權重動態遞減的方式變換權重值,改進的權重w重定義為:

(13)

其中,wmax與wmin分別表示為w可取的最大值與最小值.t為當前迭代次數,tmax為總迭代次數.其動態變化如圖2所示.

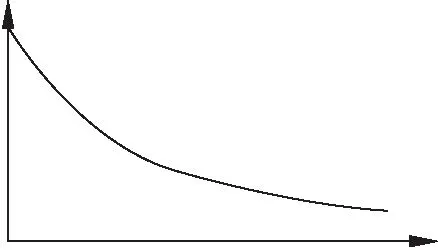
圖2 w變化曲線Fig.2 Change curve of weight

4.4 混合列交叉更新策略

標準蝙蝠算法的位置更新公式為xi(t+1)=xi(t)+vi(t+1),由于本文采用的是基于機器的編碼,直接利用上式更新蝙蝠位置會導致無效解的產生,一是由于出現小數產生無效解;二是由于超出編碼范圍產生無效解.通過4.1節的編碼方式可知,z位上的編碼基因最大值為SNz,一般的更新方式易產生無效解.因此本文提出混合列交叉更新策略,由于此策略是同一工序的加工機器交換,所以產生的必為可行解.將上式(8)更新為

xi(t+1)=xi(t)?vi(t+1)

(14)

在該式中將vi(t+1)看作索引,指向與xi(t+1)交叉的序列,交換其對應位置的元素.給出一組數據進行說明.

當x1?v1時,v1中的第一個元素為3,即指向x3的第一個元素,互換x1與x3的第一個元素;v1中的第二個元素為2,即指向x2的第二個元素,互換x1與x2的第二個元素,依此類推,對x1元素進行更新.當所有的都更新完之后,得到的新位置如下:

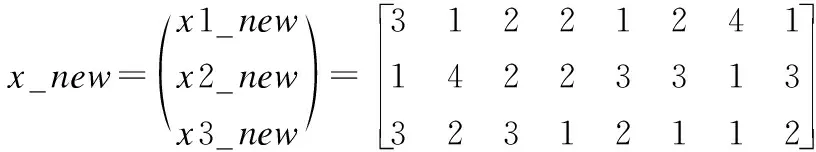
在算法初期,經過列交叉之后,種群多樣性會增加.到算法后期,所有蝙蝠都飛向最優蝙蝠,位置之間的相似度增強,更新過后算法逐漸收斂.

4.5 基于變異操作的鄰域搜索策略

算法中個體可以通過對自身以及對鄰域解進行搜查以獲取更優有解.鄰域結構的合理性體現著求解策略對問題本身特征信息的利用,影響著最終求解的效率和質量[24].因此,需要合理的設置鄰域結構.本文采取兩種基于變異操作的鄰域搜索策略.

1)基于最優排列的變異:在調度解的編碼中隨機選擇兩個位置,根據上文敘述可知每個位置上的基因有幾種,生成其所有排列,產生相應的鄰域解,選擇其中適應度值最好的個體.

2)基于機器工作量的變異:在調度解的編碼中隨機選擇兩個位置,分別對所選位置可加工的機器進行工作量的分析,選擇工作量小的機器取代原位置.

鄰域搜索的偽代碼如下:

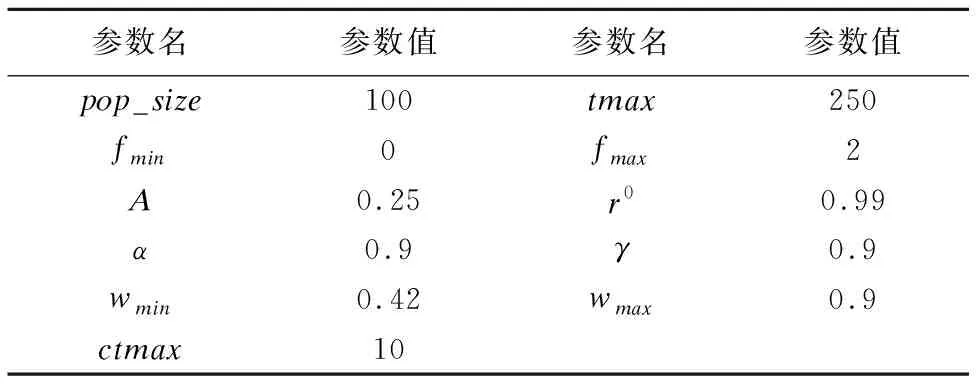
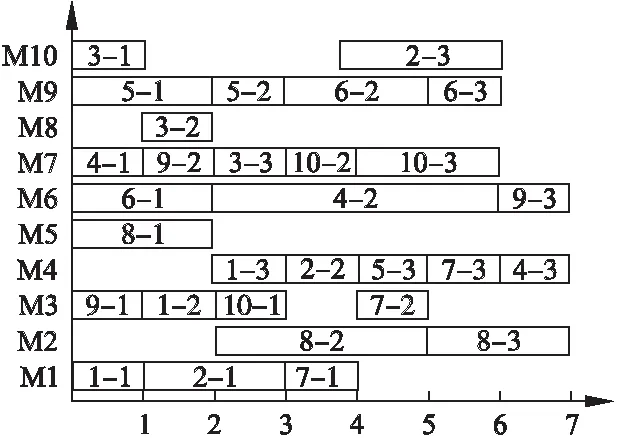
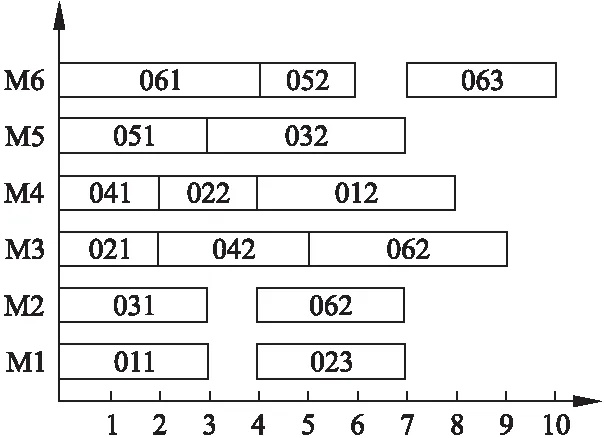
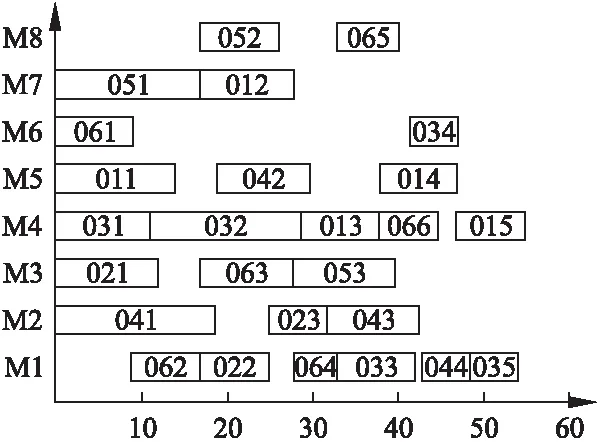
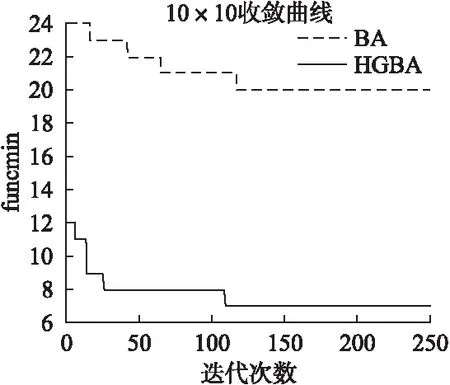
while(ct

b←rand()

if(b≥0.5)

根據方案(1)進行變異生成新的個體

else

根據方案(2)進行變異生成新的個體

endif

if新解的適應度值比舊解的適應度值好

接受新解

end if

ct←ct+1

end while

4.6 HGBA算法流程

HGBA算法具體步驟如下:

步驟1.設置參數,并且根據本文采用的編碼方式,按照4.2的初始化方法產生初始種群

步驟2.通過設定的目標函數求解每個個體的適應度值,得出當前最優解

步驟3.根據式(6)、(12)、(14)更新個體的速度與位置

步驟4.對于每個個體,當rand1>ri,則通過4.5的鄰域搜索算法對當前最優解進行擾動,產生一個新解

步驟5.若新解優于當前最優解且rand2

步驟6.更新當前最優解,并對其進行鄰域搜索

步驟7.滿足設定的最優解條件或者達到最大迭代次數,則終止程序;否則就轉到步驟3

步驟8.輸出最優解和最優值

5 實驗仿真與結果

本文實驗采用MATLAB編程,程序在Windows 10系統下內存6G的計算機上運行.算法中的參數設置如下:

表中pop_size表示初始種群規模,tmax表示總迭代次數,ctmax表示鄰域搜索的總迭代次數,fmin與fmax分別表示頻率的最小值與最大值,wmin與wmax表示權重的最小值與最大值.

為了驗證本文算法的性能,分別采用三種實例進行測試,經典10×10實例以及文獻[25]、文獻[26]中的實例.同時采用BA算法與改進算法HGBA進行比較,為了讓BA算法與HGBA相比具有可信度,BA中的相應參數設置均與HGBA相同.

表3 參數值列表Table 3 List of parameter values

實例1是經典10×10實例,它是10個工件在10臺機器上加工的完全柔性作業車間調度問題,利用本文算法求解該問題可以得到當前所知的最優解7,圖3為對應甘特圖.

圖3 10×10最優解甘特圖Fig.3 Gantt chart of optimal solutionfor 10×10

實例2是6×6實例,實驗數據來源于文獻[25],利用本文的算法求解該問題可得到全局最優解為10,該全局最優解對應的調度甘特圖如圖4.

圖4 6×6最優解甘特圖Fig.4 Gantt chart of optimal solutionfor 6×6

實例3是6×8實例,實驗數據來自文獻[26],6個工件共26道工序在8臺機器上加工.利用本文提出的HGBA對實例進行優化,得出全局最優值為55,圖5為最優解調度甘特圖.

表4中的數據均為獨立運行10次產生的.“best”列表示算法得到的最小完工時間的全局最優解,“avg”列表示10次運行得到的最優解的平均值.首先,從表中可以看出,對于經典10×10實例,HGBA算法可以得出當前最好的結果7,相對于標準BA算法,改進的HGBA算法的精度提高了61.11%.

圖5 6×8最優解甘特圖Fig.5 Gantt chart of optimal solutionfor 6×8

對于6×6實例,HGBA算法得出的全局最優值為10,與文獻[25]中的結果相比,最優解精度提高了9.09%;與BA相比,最優解精度提高了16.67%.對于6×8實例,HGBA算法得出的全局最優值為55,與文獻[26]中的結果相比,最優解精度提高了8.33%;與BA相比精度提高了6.80%.實驗數據證明了HGBA算法求解FJSP問題的有效性.

表4 測試結果Table 4 Test results

圖6 10×10收斂曲線圖Fig.6 Convergence curve for 10×10

圖6、圖7給出了用BA與HGBA分別求解10×10實例與6×8實例的全局最優解收斂圖,從圖中可以看出,由于對初始化進行改進的緣故,HGBA在剛開始迭代時就可以獲得較好的解,BA的初始解明顯較差.對于10×10實例,在迭代中能夠BA算法在得到全局最優解20處陷入局部最優,而HGBA能夠跳出局部最優繼續進化得到全局最優解7;同樣的,對于6×8實例,BA在59處陷入局部最優,HGBA能夠跳出局部最優繼續進化而得到更優質的解55.這證明了本文算法在初始化與采用的鄰域搜索的有效性.因此,本文提出的HGBA算法在求解柔性作業車間調度是有效的,可以得到良好的效果.

圖7 6×8收斂曲線圖Fig.7 Convergence curve for 6×8

6 結 論

柔性作業車間由于工序可選擇的加工機器的多樣性而變得更加的復雜,解空間更大.本文以最大完工時間最小化為目標進行柔性作業車間的優化調度,提出混合遺傳蝙蝠算法.首先,針對初始解的多樣性與質量,采用多種方式相結合來初始化種群;其次通過重定義w權重來平衡全局與局部搜索,提出基于變異的鄰域搜索策略避免陷入局部最優;同時根據本文采用的基于機器的編碼方式與調度問題的離散性問題,提出了混合列交叉策略來進行位置的更新;最后并將標準BA算法與改進算法HGBA用于求解3個實例,實驗結果對比證明了算法的有效性.然而,在實際的生產過程中,調度的好壞還受很多其他因素的影響,比如加工質量、提前/拖期等,筆者下一步將在本文的基礎上,研究多目標柔性作業車間問題.

：

[1] Brucker P,Schlie R.Job-shop scheduling with multi-purpose machines[J].Computing,1990,45(4):369-375.

[2] Garey M R,Johnson D S,Sethi R.The complexity of flow- shop and jobshop scheduling[J].Mathematics of Operations Research,1976,1(2):117-129.

[3] Liu Xiao-bing,Jiao Xuan,Ning Tao,et al.Improved methodof flexible job shop scheduling based on double chains quantum genetic algorithm[J].Computer Integrated Manufacturing System,2015,21(2):495-502.

[4] Taisch M.Multi-objective genetic algorithm for energy-efficient job shop scheduling[J].International Journal of Production Research,2015,53(23):7071-7089.

[5] Zhang Teng-fei,Ma Yue,Li Li,et al.Improved genetic algorithm for flexible job shop scheduling problem[J].Journal of Chinese Computer Systems,2017,38(1):129-132.

[6] MinseokSeo,Daecheol Kim.Ant colony optimisation with parameterised search space for the job shop scheduling problem[J].International Journal of Production Research,2010,48(4):1143-1154.

[7] Tian Song-ling,Chen Dong-xiang,Wang Tai-yong,et al.An asynchronous parallel ant colony optimization for flexible job-shop scheduling problem[J].Journal of Tianjin University(Science and Technology),2016,49(9):920-928.

[8] Zhang Qi-liang,Chen Yong-sheng.Hybrid PSO-NEH algorithm for solving no-waitflexible flow shop scheduling problem[J].Systems Engineering-theory & Practice,2014,34(3):802-809.

[9] Zhong Yu-jiang,Yang Hai-cheng,Mo Rong,et al.Optimization method of flexible job-shop scheduling problem based on niching and particle swarm algorithms [J].Computer Integrated Manufacturing System,2015,21 (12):3231-3238.

[10] Li Xiu-lin,Lu Jian-sha,Chai Guo-zhong,et al.Hybrid bee colony algorithm for flexible Job Shop scheduling problem[J].Computer Integrated Manufacturing System,2011,17 (7):1495-1500.

[11] Zhao Shi-kui.Bilevel neighborhood search hybrid algorithm for the flexible job shop scheduling problem[J].Journalof Mechanical Engineering,2015,51(14):175-184.

[12] Wu Xiu-li,Zhang Zhi-qiang,Du Yan-hua,et al.Improved bacteria foraging optimization algorithm for flexible job shop scheduling problem[J].Computer Integrated Manufacturing System,2015,21(5):1262-1270.

[13] Gao K Z,Suganthan P N,Pan Q K,et al.Discrete harmony search algorithm for flexible job shop scheduling problem with multiple objectives[J].Journal of Intelligent Manufacturing,2016,27(2):363-374.

[14] Yang X S.A new metaheuristic bat-inspired algorithm [M].Nature Inspired Cooperative Strategies Foroptimization,Berlin:Springer,2010:65-74.

[15] Li Zhi-yong,Ma Ling,Zhang Hui-zhen.Quantum bat algorithm for function optimization[J].Journal of Systems & Management,2014,23(5):717-722.

[16] Chen Y T,Tsai M T,Liao B Y,et al.An echo-aided bat algorithm to construct topology of spanning tree in wireless sensor networks[M].Intelligent Data Analysis and Its Applications,Springer International Publishing,2014:451-462.

[17] Goyal S,Patterh M S.Modified bat algorithm for localization of wireless sensor network[J].Wireless Personal Communications,2016,86(2):1-14.

[18] Lin Jun-hao,Zhang Yan,Chen Si,et al.Optimal DG allocation considering effect of controllable load for active distribution system[J].Electric Power Automation Equip-ment,2016,36(9):46-53+73.

[19] Yang Jia-ran,Wang Xin-cheng,Jiang Cheng,et al.Multi-objective dynamic optimal scheduling of power system considering wind power risk[J].Power System Protection Control,2016,44(7):25-31.

[20] Xia Jing-jing,Wang Meng.Improved bat algorithm for job shop scheduling problem[J].Journal of HuaZhong Normal University(Natural Sciences),2016,50(4):536-543.

[21] Han Zhong-hua,Zhu Bo-qiu,Shi Hai-bo,et al.Study for flexible flow shop scheduling problem with based on advanced bat algorithm[J].Application Research of Computers,2017,33(7):1-6.

[22] Luo Q,Zhou Y,Xie J,et al.Discrete bat algorithm for optimal problem of permutation flow shop scheduling [J].Scientific World Journal,2014,2014:1-15.

[23] Dao T K,Pan T S,Nguyen T T,et al.Parallel bat algorithm for optimizing makespan in job shop scheduling problems[J].Journal of Intelligent Manufacturing,2015:1-12.

[24] Zhao Shi-kui,Fang Shui-liang.Operation-based encoding and neighborhood search genetic algorithm for job shop scheduling optimization[J].Journal of Mechanical Engineering,2013,49(16):160-169.

[25] Peng Jian-gang,Liu Ming-zhou,Zhang Ming-xin,et al.Cloud model evolutionary multi-objective flexible job-shop scheduling based on improved non-dominated sorting[J].Journalof Mechanical Engineering,2014,50(12):198-205.

[26] Kong Fei,Wu Ding-hui,Ji Zhi-cheng.Flexible job-shop scheduling optimization based on two-layer particle swarm optimization algorithm[J].Journal of Computer Applications,2015,35(2):476-480.

附中文參考文獻：

[3] 劉曉冰,焦 璇,寧 濤,等.基于雙鏈量子遺傳算法的柔性作業車間調度[J].計算機集成制造系統,2015,21(2):495-502

[5] 張騰飛,馬 躍,李 力,等.柔性作業車間調度問題的改進遺傳算法[J].小型微型計算機系統,2017,38(1):129-132.

[7] 田松齡,陳東祥,王太勇,等.一種異步蟻群算法求解柔性作業車間調度問題[J].天津大學學報(自然科學與工程技術版),2016,49(9):920-928.

[8] 張其亮,陳永生.基于混合粒子群-NEH算法求解無等待柔性流水車間調度問題[J].系統工程理論與實踐,2014,34(3):802-809.

[9] 仲于江,楊海成,莫 蓉,等.基于小生境粒子群算法的柔性作業車間調度優化方法[J].計算機集成制造系統,2015,21(12):3231-3238.

[10] 李修琳,魯建廈,柴國鐘,等.混合蜂群算法求解柔性作業車間調度問題[J].計算機集成制造系統,2011,17(7):1495-1500.

[11] 趙詩奎.求解柔性作業車間調度問題的兩級鄰域搜索混合算法[J].機械工程學報,2015,51(14):175-184.

[12] 吳秀麗,張志強,杜彥華,等.改進細菌覓食算法求解柔性作業車間調度問題[J].計算機集成制造系統,2015,21(5):1262-1270.

[15] 李枝勇,馬 良,張惠珍.函數優化的量子蝙蝠算法[J].系統管理學報,2014,23(5):717-722.

[18] 林君豪,張 焰,陳 思,等.考慮可控負荷影響的主動配電系統分布式電源優化配置[J].電力自動化設備,2016,36(9):46-53+73.

[19] 楊家然,王興成,蔣 程,等.計及風力發電風險的電力系統多目標動態優化調度[J].電力系統保護與控制,2016,44(7):25-31.

[20] 夏晶晶,王 猛.面向作業車間調度問題的改進型蝙蝠算法[J].華中師范大學學報(自科科學版),2016,50 (4):536-543.

[21] 韓忠華,朱伯秋,史海波,等.基于改進蝙蝠算法的柔性流水車間排產優化問題研究[J].計算機應用研究,2017,33(7):1-6.

[24] 趙詩奎,方水良.基于工序編碼和鄰域搜索策略的遺傳算法優化作業車間調度[J].機械工程學報,2013,49(16):160-169.

[25] 彭建剛,劉明周,張銘鑫,等.基于改進非支配排序的云模型進化多目標柔性作業車間調度[J].機械工程學報,2014,50(12):198-205.

[26] 孔 飛,吳定會,紀志成.基于雙層粒子群優化算法的柔性作業車間調度優化[J].計算機應用,2015,35(2):476-480.