無設備定位的射頻層析成像求逆算法研究

錢 慧，劉煥林

（福州大學 物理與信息工程學院，福建 福州 350116）

0 引 言

隨著物聯網技術的不斷進步，未來傳感器節點的數量將呈現爆炸式增長，這種趨勢下，物聯網為人類提供的業務種類會越來越多[1-3]。無線傳感網絡（Wireless Sensor Network，WSN）是物聯網的重要組成部分，利用其實現對網絡區域內目標的定位已成為研究熱點之一。射頻層析成像（Radio Tomographic Imaging， RTI）以無線通信傳輸的衰減模型為基礎，是一種新興的用于對WSN中物體造成的衰減進行成像的技術。自2009年美國猶他大學學者Joey Wilson和Neal Patwari提出該技術以來，本領域的研究重心主要集中在室內外定位、目標追蹤和模式識別方面[4-6]。為提升系統性能，研究人員針對重構算法、物理模型進行了深入的研究[7-10]。目前該技術主要應用于室內定位，在不同的應用場景下如何選取重構算法對RTI系統的推廣至關重要[11]。

一般情況下，時間開銷和空間開銷是評價算法好壞的主要評價指標。時間開銷越小，算法的計算速度越快，越有利于實現數據的實時處理；空間開銷越小，算法對計算機內存的占用率越小，不會過多地影響其并行處理。結合RTI系統的自身情況，實現數據地的實時處理有利于對目標的準確追蹤，因此時間開銷是首要考慮的因素。相比之下，由于算法的輸入數據量不是很大，因此空間開銷并非十分重要。除此之外，RTI重構算法還需兼顧算法的性能和重構信號質量。與常規室內定位不同的是，RTI系統輸出的是二維圖像信號，具有可視化功能，噪聲的形式和大小對人的主觀判斷至關重要。就RTI系統而言，可采用定位穩定性和定位誤差評價系統性能。

本文采用ZigBee節點搭建無線傳感網絡，采集實地接收信號強度值（Received Signal Strength，RSS）。利用計算機仿真的優勢，對典型的三種重構算法（Tikhonov正則化、k-SVD和TV正則化）從計算時間、圖像質量、系統性能和重構圖像尺寸四個方面進行了系統性分析，在分析圖像質量部分引入了全參考圖質量評價方法。

1 系統設計

RTI系統網絡部署如圖1所示。考慮該WSN中的某條通信鏈路i，鏈路上接收節點的RSS值yi（t）有五種主要因素的影響：發送節點的功率（Pi）；由收發節點之間的距離、天線模式等造成的靜態損耗（Li）；物體阻擋造成的陰影損耗（Si（t））；多徑效應的影響（Fi（t））；RSS測量噪聲與模型不理想造成的影響（vi（t））。

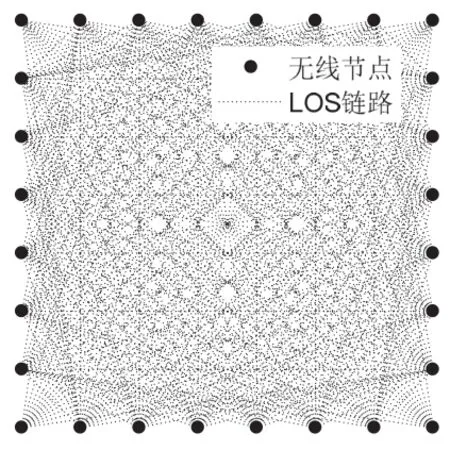
圖1 RTI系統網絡布置示意圖

其中，Pi和Li可近似地認為不隨時間變化；為了簡化問題，本文只考慮視距鏈路（Line of Sight， LoS）上的衰減，所以Fi（t）和vi（t）可被看成是RTI系統的噪聲項。接收節點的RSS值可被描述成如下形式：

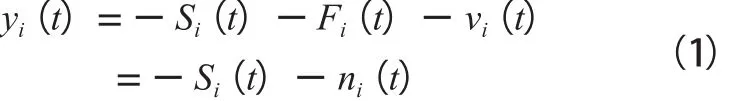
進一步考慮陰影損耗Si（t）：

其中：xj（t）表示在t時刻發生在像素j上的衰減；wij表示像素j上發生的衰減對鏈路i上RSS值大小的影響。一般情況下，RTI系統工作時，WSN工作在兩種狀態，即空狀態和工作狀態。空狀態是WSN區域在系統工作前所處的一種狀態。基于衰減模型的RTI系統的工作原理是：利用區域內工作狀態和空狀態下電磁場的變化實現對人們行為的感知：

至此僅考慮了WSN中的一條通信鏈路，為了說明整個系統，下文將采用矩陣的形式：

其中，

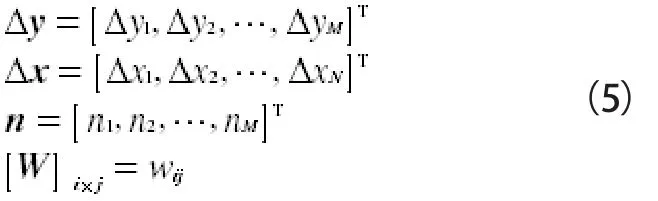
式（4）中W的維數為M×N，M代表無向鏈路的條數，N為重構圖的像素個數，i代表鏈路標號，j為像素的標號。W是RTI系統的關鍵部分，稱作系統模型，本文引用文獻[3]中提出的歸一化橢圓模型計算。該模型認為：以收發節點為焦點的橢圓區域內存在權重，權重大小與收發節點有關，此區域外的權重均為零。該模型被定義如下：

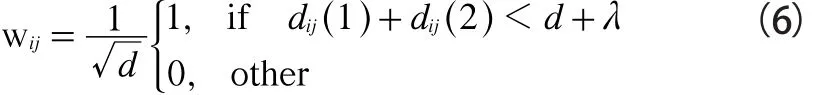
其中：d是第i條鏈路收發節點之間的距離，dij（1）和dij（2）分別為第j個像素的中心點到第i條鏈路收發節點之間的距離，λ是一個調節橢圓寬度的可控變量。

2 重構算法

許多物理線性模型都可以進行如下描述：

其中：y∈RM是測量數據，W∈RM+N是變換矩陣，n∈RM是測量噪聲向量，x∈RN是待求解信號，這里M＜N。由于M＜N，式（7）存在著無窮解，即已知y和W時，無法求x的唯一解。本文將RSS的變化值表示為y，像素區域電磁場相對于空狀態的變化值表示為x，這樣式（4）和（7）等價。正則化方法是求解病態反問題的主要工具。

正則化的思想是：通過添加正則化項，達到約束解的范圍的目的。正則化方法需要已知x的先驗知識g（x）。通常利用正則化方法求解問題（7），即求解式（8）：

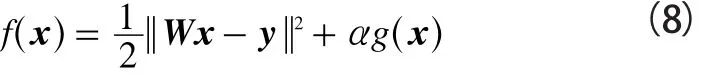
式（9）和式（10）分別為Tikhonov和TV正則化的約束項：

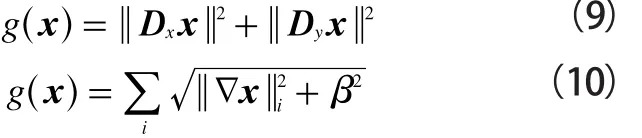
在RTI系統中，Dx和Dy分別為重構圖的橫向和豎向差分運算符。從式（9）和（10）中不難發現，Tikhonov正則化方法通過化簡可轉化成線性問題（11），TV正則化是一個非線性求解過程：

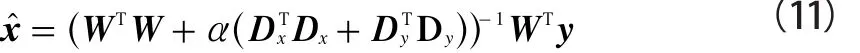
RTI成像問題是一個病態問題。在病態系統中，輸入數據y的微小變化都有可能使重構信號x發生巨大變化，導致整個系統變得非常不穩定。這一點可通過對W做奇異值分解（Singular Value Decomposition，SVD）直觀地看出來：

其中：U和V是酉矩陣，Σ是奇異值矩陣。k-SVD算法通過剔除模型矩陣W中較小的奇異值，保留其中前k個主要成分實現求解：

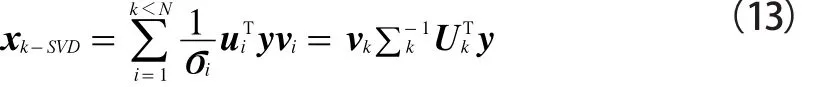
奇異值向量取決于系統本身（像是系統模型），使得該算法的求解往往與期望解偏差較大，這是因為它沒有用到x的先驗知識。

圖2 RTI重構圖與參考圖

利用正則化方法求解病態反問題十分有效，在不少領域已得到成功應用，如熱傳導、地質勘探等。圖2中給出了采用奇異值分解方法（圖（c），（d））和正則化方法得到的重構圖 （圖（b）），其中圖（a）為參考圖。不難發現，不同的約束直接影響著重構圖的質量。與SVD方法相比，通過正則化方法得到的圖更接近參考圖。

3 仿真分析

RSS值測量平臺搭建：20個由TI公司制造的ZigBee無線節點部署在20.25 m2的平地上，每個節點沿著4.5 m的邊長間隔0.9 m分開放置在距離地面1 m的位置上。無線節點工作在2.4 GHz頻段上，并使用IEEE 802.15.4標準通信。系統中的節點采用輪詢廣播方式收發信息，掃描速率為3圈/秒。實驗中采用木質立桿搭載無線節點，可以有效減小立桿對測量數據質量的影響。該平臺的實景如圖3所示。

圖3 RTI系統網絡布置實景圖

RSS值測量獲取：搭建上述平臺后，在保證平臺穩定工作的前提下，先讓其處于空狀態下工作30 min，并將所有接收到的RSS值保存在文件中，求其平均值yNULL。此后測試人員在一些固定的測試點上分別站立10 min，共得到650個可用數據 y（i）。Δy（i）=y（i）-yNULL便是后續實驗所需的 RSS 值。在后續重構過程中用到的參數值見表1所列。RH為構造參考圖時選用的人體半徑。

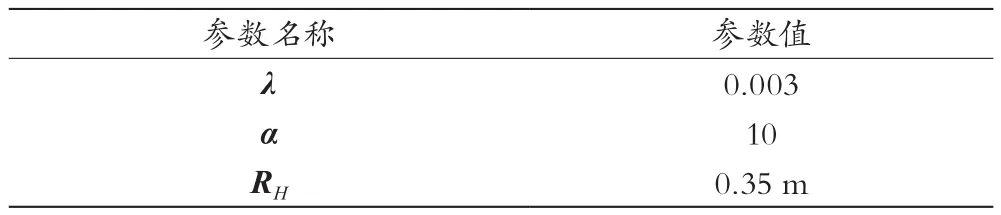
表1 圖像重構參數

通過分析算法運行時間可得到圖4。相比于非線性算子對應的TV正則化方法，在計算時間上Tikhonov正則化占據著絕對優勢，且隨著重構圖尺寸的增大，后者完全可滿足實時性要求，TV正則化方法的計算時間會隨著圖像尺寸的增加呈指數增長。

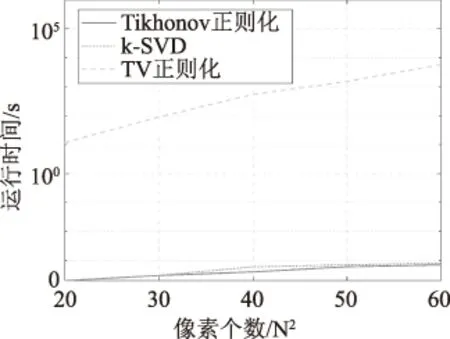
圖4 三種算法運行時間比較

圖像質量與RTI系統性能緊密關聯，它的好壞直接影響著人的主觀視覺。在RTI定位系統中，圖像中位置亮斑與噪聲亮斑之間的相對大小及位置即圖像質量好壞的直接體現。一般地，信號質量評估指標均方誤差（Mean Square Error，MSE）此時將失效，所以本文采用結構相似性度量（Structural Similarity Index， SSIM）作為圖像質量評價指標[11-13]。三種算法下圖像質量隨像素尺寸變化的趨勢如圖5所示。

在RTI定位系統中，依據最大值定位準則（將圖像中亮度值最大的位置作為目標位置）可不依賴人眼得到目標位置。在這種客觀的定位方法中，明顯處于劣勢。三種算法定位精度與可靠性比較分別如圖6、圖7所示。從圖6和圖7中可以看出，奇異值分解法在定位精度和系統可靠性方面都不及正則化方法。此時，TV正則化方法在定位精度和系統可靠性方面都優于剩余兩種方法。

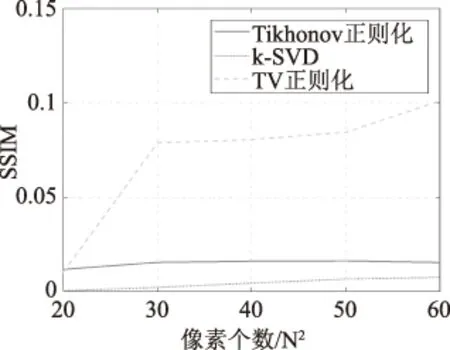
圖5 三種算法所得重構圖質量比較

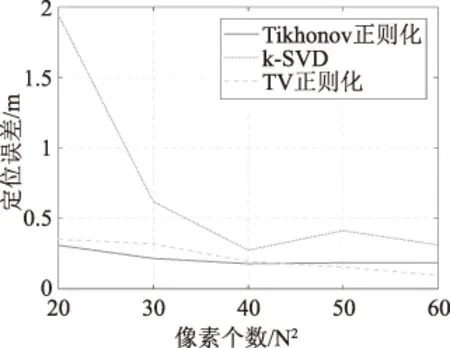
圖6 三種算法定位精度比較

圖7 三種算法定位可靠性比較

4 結 語

物聯網技術的發展促進了RTI技術的深入研究，選取適當的重構算法有利于該技術的推廣。本文對三種典型重構算法進行了仿真實驗，仿真結果表明：不存在絕對完美的RTI重構算法，線性算子有利于降低計算時間，非線性算子有利于提高圖像質量和系統性能。實際應用中可根據特定應用場景選取恰當的RTI重構算法，以利于節省資源。

[1]汪苑，林錦國.幾種常用室內定位技術的探討[J].中國儀器儀表，2011（2）：54-57.

[2]李同松.基于ZigBee技術的室內定位系統研究與實現[D].大連：大連理工大學， 2008.

[3]顧晶晶，陳松燦，莊毅.基于無線傳感器網絡拓撲結構的物聯網定位模型[J].計算機學報，2010，33（9）：1548-1556.

[4] WILSON J， PATWARI N. Radio tomographic imaging with wireless networks[J].IEEE transactions on mobile computing， 2010，9（5）：621-632.

[5] WILSON J， PATWARI N， VASQUEZ F G. Regularization methods for radio tomographic imaging[Z]. Virginia tech symposium on wireless personal communications， 2009.

[6]王滿意.基于無線傳感器網絡的無線層析成像定位技術的研究[D].北京：中國礦業大學， 2015.

[7] KANSO M A， RABBAT M G. COMPRESSED RF Tomography for wireless sensor networks：centralized and decentralized approaches[C]// IEEE international conference on distributed computing in sensor systems. springer-verlag， 2009：173-186.

[8] YANG L， HUANG K， WANG G， et al. An enhanced multiscale model for shadow fading in radio tomographic imaging[C]//Intelligent control and automation. IEEE， 2015：5925-5930.

[9] KE W， WANG T， SHAO J. CS-based device-free localization in the presence of model errors[C]// IEEE International conference on acoustics， speech and signal processing. IEEE， 2016：4443-4447.

[10] HAMILTON B R， MA X， BAXLEY R J， et al. Propagation modeling for radio frequency tomography in wireless networks[J].IEEE journal of selected topics in signal processing， 2014，8（1）：55-65.

[11] SAVAZZI S， SIGG S， NICOLI M， et al. Device-Free radio vision for assisted living： leveraging wireless channel quality information for human sensing[J]. IEEE signal processing magazine， 2016， 33（2）：45-58.

[12] WANG Z， BOVIK A C， LU L. Why is image quality assessment so difficult？[C]// IEEE international conference on acoustics，speech， and signal processing. IEEE， 2002：IV-3313-IV-3316.[13] WANG Z， BOVIK A C. Mean squared error： Love it or leave it？A new look at signal fidelity measures[J]. IEEE signal processing magazine， 2009，26（1）：98-117.