基于EEMD_SVM的波紋管壓漿超聲檢測
,,
(河海大學(xué) 物聯(lián)網(wǎng)學(xué)院, 常州 213022)
橋梁的安全與內(nèi)部波紋管的壓漿質(zhì)量息息相關(guān),在波紋管內(nèi)部灌入水泥漿后,由于灌漿工藝以及環(huán)境等因素的影響,波紋管內(nèi)部鋼絞線附近的水泥漿可能脫落而出現(xiàn)空腔,形成脫漿缺陷。由于波紋管壁和混凝土材料對聲波信號的衰減作用,超聲檢測獲取的反射信號包含的缺陷信息較為微弱,且聲波在混凝土中會發(fā)生不同程度的散射、反射、折射,這些因素會對回波造成復(fù)雜的影響,從而使得通過回波信號很難直接觀察出波紋管內(nèi)部是否存在缺陷,因此,如何有效快速地判斷波紋管內(nèi)部的注漿程度,是實際檢測過程中的一大難點[1-2]。
筆者提出將信號的總體平均經(jīng)驗?zāi)B(tài)分解(EEMD)用于波紋管的質(zhì)量檢測中,其適用于常見的非平穩(wěn)、非線性信號的分解與處理,是一種自適應(yīng)的分解方法,信號通過EEMD分解,可以得到多個不同頻帶的本征模態(tài)分量(IMF)。波紋管內(nèi)部出現(xiàn)缺陷時,缺陷位置的信息會隱藏在超聲回波信號中,不同IMF分量信號的能量分布會發(fā)生相應(yīng)改變。文章采用了EEMD分解與支持向量機(SVM)相結(jié)合的波紋管壓漿質(zhì)量檢測方法,將包含主要信息的IMF分量中提取出來的能量熵特征作為SVM的輸入,建立支持向量機分類機制,判斷波紋管的壓漿質(zhì)量。結(jié)果表明,該方法能有效地判斷波紋管內(nèi)部是否出現(xiàn)嚴(yán)重空腔缺陷。
1 EEMD和支持向量機理論
1.1 EEMD能量熵理論
EEMD的分析引入了白噪聲的特性,由于EMD[3](經(jīng)驗?zāi)B(tài))分解過程會出現(xiàn)模態(tài)混疊問題,而高斯白噪聲具有均勻分布的特點,加入了白噪聲的信號在各個尺度上會具有連續(xù)性,有效地避免了EMD方法的缺陷。
EEMD的分解如下[4]:
(1) 初始化EMD分解次數(shù)M和白噪聲幅值系數(shù)k(取值范圍0.1~0.4),設(shè)EMD初次分解次數(shù)m為1。
(2) 在原序列x(t)上加入隨機高斯白噪聲序列nm(t),得到加噪的待處理的第m個序列。
xm(t)=x(t)+knm(t)
(1)
對xm(t)進(jìn)行EMD分解,得到n個IMF分量cim(t)和一個剩余分量rnm(t),分別為
cim(t)=hjm(t)i=1,2,3,…,n
(2)
rnm(t)=rn-1m(t)-cnm(t)
(3)
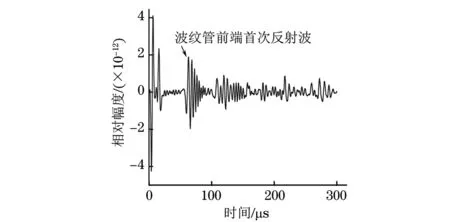
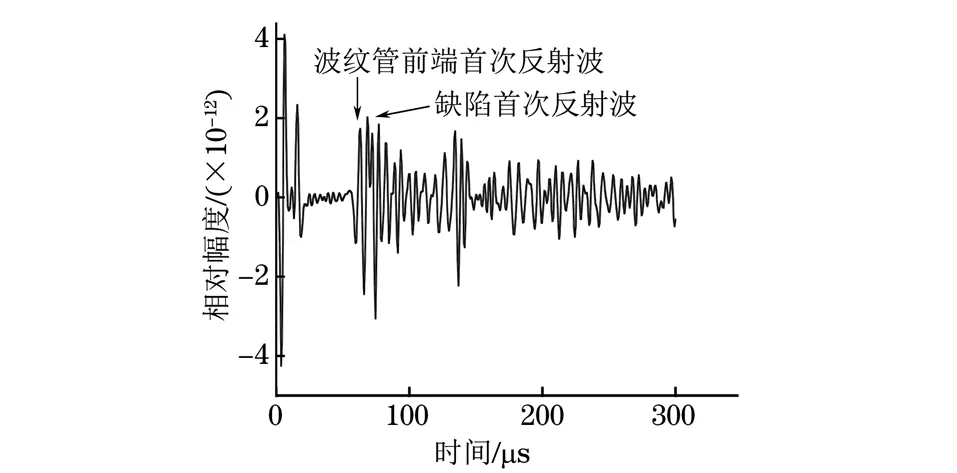
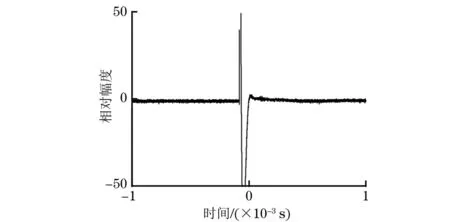
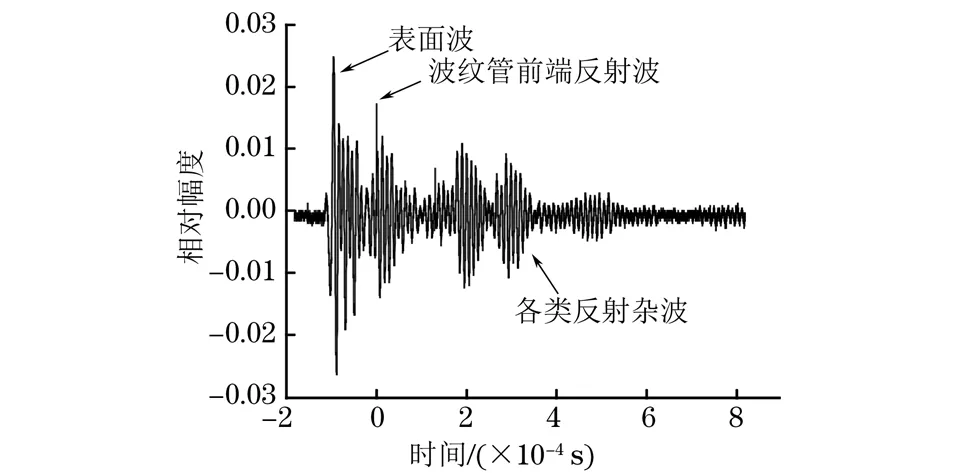
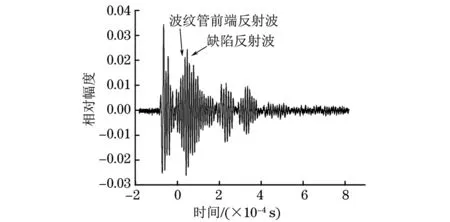
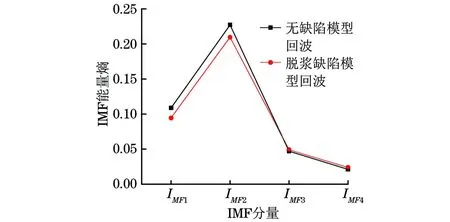
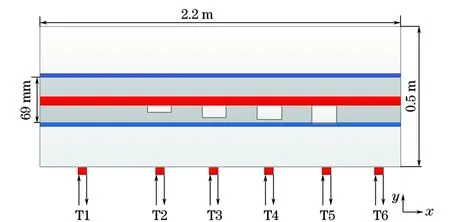
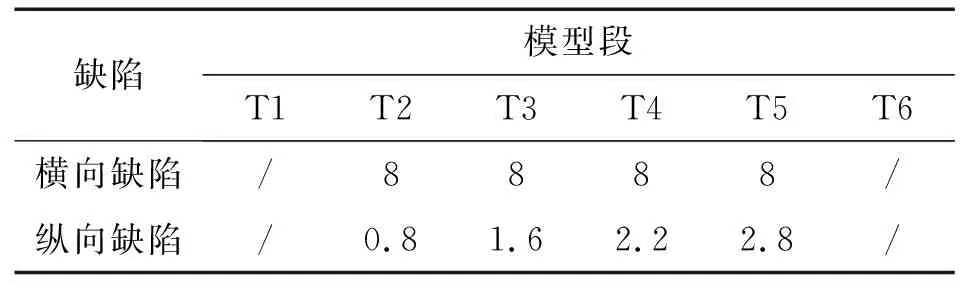
若m (3) 對M次EMD試驗的所有IMF分量以及剩余分量計算平均值為如下式所示。 (4) (5) 通過EEMD得到分解后的各個頻段,以不同分量信號的能量熵表示信號能量分布。 (1) 計算分解后各個尺度信號(IMF1到IMFn)的能量值Ei,總能量如式(6)所示。 (6) (2) 每個IMF分量信號能量所占概率為Pi=Ei/E,得出每一個IMF信號的能量熵如式(7)所示。 H(IMFi)=-PilogePi[5] (7) 支持向量機的分類思想為:在樣本線性可分時,直接在原空間構(gòu)造數(shù)據(jù)樣本的最優(yōu)分類超平面。若樣本線性不可分,則在原空間中引入松弛變量,通過非線性變換將低維空間的數(shù)據(jù)樣本映射到高維空間,即經(jīng)過已選擇的非線性映射將輸入向量映射到一個高維的特征空間,然后在這個空間里面建立一個最優(yōu)的分類超平面,SVM分類函數(shù)實際上相當(dāng)于神經(jīng)網(wǎng)絡(luò)[6-7]。 輸出的決策準(zhǔn)則為 (8) 權(quán)值wi=αiyi,K(x·xi)為基于n個輸入向量x1,x2,…,xn的非線性變換,也即SVM中的內(nèi)積核函數(shù)。 常用的內(nèi)積核函數(shù)有: (1)多項式核函數(shù) K(x,xi)=[(x·xi)+1]q (9) (2)徑向基函數(shù)(RBF) K(x,xi)=exp{-|(x-xi)2/σ2|} (10) (3) S形核函數(shù) K(x,xi)=tanh[v(x·xi)+c] (11) 事先從無缺陷模型和完全脫漿的波紋管模型中提取超聲檢測信號,作為試驗組信號,采取EEMD聯(lián)合支持向量機方法來判斷模型是否產(chǎn)生嚴(yán)重脫漿,實施步驟為: (1) 對試驗組各取n組波回波信號的m個主要分量能量熵,組成訓(xùn)練集,輸入支持向量機進(jìn)行訓(xùn)練,得到分類器。 (2)對待檢測的波紋管同樣提取信號m個主要分量的能量熵,輸入分類器,支持向量機根據(jù)分類準(zhǔn)則對輸入的向量進(jìn)行分類,判斷原信號所屬模型的缺陷情況。 波紋管壓漿結(jié)構(gòu)系統(tǒng)的模型如圖1所示,其最外層為混凝土層,其次為波紋管,在波紋管內(nèi)部注入了水泥漿,在鋼絞線附近可能出現(xiàn)水泥漿脫落的情況,即出現(xiàn)脫漿缺陷而產(chǎn)生空腔,脫漿的空腔越大,脫漿程度越嚴(yán)重。超聲波在傳播時,遇到不同介質(zhì)會發(fā)生反射、透射以及散射等一系列物理現(xiàn)象。由于空氣與混凝土等材料的聲阻抗特性相差較大,超聲經(jīng)過混凝土/空氣等界面時會發(fā)生較強的反射,空腔缺陷信息會隱藏在反射回波信號中,而利用超聲波脈沖回波法獲取信號中的有效信息,則能實現(xiàn)對缺陷的檢測。 圖1 波紋管結(jié)構(gòu)示意 首先采取仿真分析,建立不同波紋管壓漿模型,采用COMSOL Multiphysics仿真軟件[8]進(jìn)行仿真,圖2為建立的6個不同的二維仿真模型,A0~A5代表實際過程中不同脫漿程度的波紋管結(jié)構(gòu),其中,A0代表無缺陷模型,A5代表完全脫漿模型;模型各段空腔缺陷尺寸如表1所示。仿真中以線源作為激勵源,模擬實際過程中的發(fā)射換能器,寬度為2cm,使用自發(fā)自收模式獲取模型回波信號,激勵信號S(t)采用漢寧窗調(diào)制的單脈沖信號,如下式所示。 (t 式中:f為信號中心頻率,f=200 kHz;t0=10 μs。 圖2 波紋管壓漿仿真模型 表1 仿真模型各段空腔缺陷的尺寸 cm 分別以A0模型及A5模型超聲回波信號(見圖3和圖4)為例進(jìn)行分析,由于波紋管復(fù)雜結(jié)構(gòu)的作用,回波信號較為復(fù)雜,A5模型回波信號中,缺陷回波隱藏在波紋管反射波等復(fù)雜波形中,難以直觀判斷,因此需要采用必要的信號處理手段來提取有用信息。 圖3 A0模型的仿真回波信號 圖4 A5模型的仿真回波信號 采用文章提出的方法對信號進(jìn)行EEMD分解,圖5為A0信號分解后的波形,圖6為A0、A5模型仿真信號的前4個主要IMF分量的能量熵分布。仿真信號的分析表明,波紋管結(jié)構(gòu)缺陷的信息可以由回波信號的能量熵分布體現(xiàn)出來,提取兩種模型回波信號主要分量的能量熵,作為試驗組輸入向量建立分類機,設(shè)置A0模型數(shù)據(jù)組成的特征向量對應(yīng)類別標(biāo)簽為+1,A5模型數(shù)據(jù)對應(yīng)類別標(biāo)簽為-1,可以用來判斷其他仿真模型缺陷情況,分類結(jié)果為:A1,+1;A2,+1;A3,-1;A4,-1。 圖5 A0模型回波信號各頻段分量 圖6 A0,A5模型信號的主要能量熵分布 從支持向量機分類結(jié)果可看出,A3、A4的分類結(jié)果為-1,表明這兩種模型較為接近A5模型,判定其中有嚴(yán)重脫漿;A1、A2模型結(jié)果為+1,比較接近A0模型。仿真結(jié)果表明,此方法較適用于尺寸較大的缺陷的檢測。 圖7 實際澆筑模型 圖8 實際試驗的激勵信號 圖9 無缺陷模型實測回波 圖10 脫漿模型實測回波 試驗?zāi)P褪前凑赵O(shè)計好的缺陷位置及類型進(jìn)行澆筑的混凝土結(jié)構(gòu),如圖7所示,其中,波紋管內(nèi)徑為69 mm,波紋管壁的厚度為3 mm,試件尺寸(長×寬×高)為10 m×0.5 m×1 m,內(nèi)置不同程度的脫漿缺陷。激勵源采用單脈沖激勵,激勵信號如圖8所示,發(fā)射換能器中心頻率為200 kHz,采用一發(fā)一收模式獲取超聲回波數(shù)據(jù),采樣頻率為1 MHz,獲得的一組測量信號如圖9,10所示。由圖9,10可見,脫漿模型的缺陷回波信號隱藏在波紋管反射信號等復(fù)雜波形中,由于實際過程中脫漿程度不同,回波信號的缺陷回波時刻和幅度也有所差別,且受各種因素影響,難以通過復(fù)雜的波形直觀判斷出波紋管壓漿質(zhì)量。和仿真結(jié)果類似,通過EEMD分解后的信號能量熵(見圖11)能夠作為區(qū)別兩種信號的指標(biāo)。采取仿真的方法來判斷壓漿質(zhì)量,首先建立試驗組,即事先采集無缺陷模型和完全脫漿模型回波信號各20組樣本,將此20組信號組成的特征向量作為訓(xùn)練集輸入,得到分類機,設(shè)置無缺陷模型特征向量對應(yīng)類別標(biāo)簽為+1,完全脫漿模型對應(yīng)類別標(biāo)簽為-1。 圖11 實測信號的主要能量熵分布 圖12 試驗測試模型 建立分類器后,試驗測試模型如圖12所示,采集實際測量模型信號,檢驗SVM測試結(jié)果,試驗檢測T1~T6段模型。試驗?zāi)P透鞫慰涨蝗毕莩叽缛绫?所示,分類結(jié)果如表3所示,試驗結(jié)果驗證了仿真結(jié)果,結(jié)果表明T3~T5段有較嚴(yán)重的脫漿缺陷,而T2的缺陷無法識別出來,驗證了仿真理論,也表明此方法適用于大缺陷的檢測,而在實際工程中,脫漿程度較小時的安全隱患較低。此方法通過超聲脈沖回波法獲取波紋管結(jié)構(gòu)信息,經(jīng)EEMD分解結(jié)合SVM分類結(jié)果即可初步判斷壓漿質(zhì)量,能夠較為直觀地檢測出波紋管是否有嚴(yán)重脫漿,適用于工程檢測。 表2 試驗?zāi)P透鞫慰涨蝗毕莩叽?cm 表3 試驗測試模型的SVM分類結(jié)果 EEMD是一種自適應(yīng)的非線性分解方法,能夠有效地提取波紋管超聲回波信號的特征,通過EEMD分解后的各頻段信號的能量熵特征能夠反映模型內(nèi)部缺陷特征,SVM分類機制和EEMD結(jié)合的方法能夠有效地判斷波紋管內(nèi)部是否存在嚴(yán)重空腔缺陷,但如何精確判別小缺陷的有無及所在位置還需作進(jìn)一步的研究。 參考文獻(xiàn): [1] 成錦, 韓慶邦, 范洪輝,等. 基于小波熵技術(shù)的波紋管壓漿質(zhì)量無損檢測[J]. 壓電與聲光, 2014, 36(6):1025-1029. [2] 高小妮, 謝峻 , 安寧,等.基于不同雷達(dá)天線的橋梁深層鋼筋識別精度試驗[J]. 無損檢測, 2017, 39(11):44-47. [3] JONG-HYO A, DAE-HO K, BONG-HWAN K. Fault detection of a roller-bearing system through the EMD of a wavelet denoised signal[J]. Sensors, 2014, 14(8):15022-15038. [4] WANG T, ZHANG M, YU Q, et al. Comparing the application of EMD and EEMD on time-frequency analysis of seimic signal[J]. Journal of Applied Geophysics, 2012, 83(6):29-34. [5] LIU Z, CUI Y, LI W. A classification method for complex power quality disturbances using EEMD and rank wavelet SVM[J]. IEEE Transactions on Smart Grid, 2015, 6(4):1678-1685. [6] 吳慶偉, 王金龍, 張平. 基于FOA-SVM模型的輸油管道內(nèi)腐蝕速率預(yù)測[J]. 腐蝕與防護(hù), 2017, 38(9):732-736. [7] LIAN Y, LI Y W, QUAN Z, et al. SVM strategies for common-mode current reduction in transformerless current-source drives at low modulation index[J]. IEEE Transactions on Power Electronics,2016,32(2):1312-1323. [8] HAN Q, CHENG J, FAN H, et al. Ultrasonic nondestructive testing of cement grouting quality in corrugated pipes based on impact-echo[J].Journal of Advanced Concrete Technology,2014,12(11):503-509.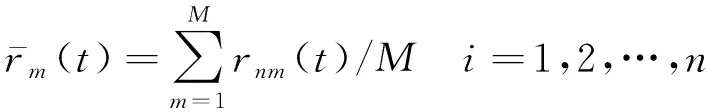
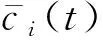
1.2 支持向量機理論
1.3 聯(lián)合判別方法
2 波紋管仿真分析
2.1 仿真模型及聲測量原理

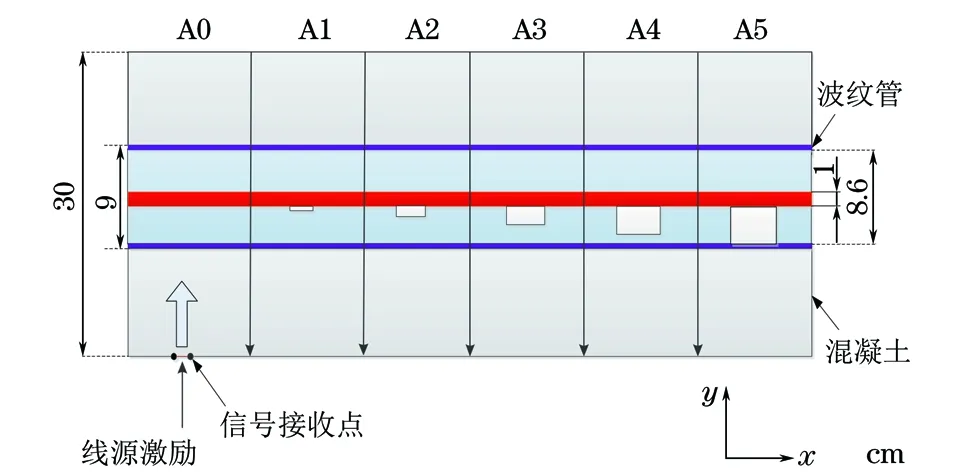
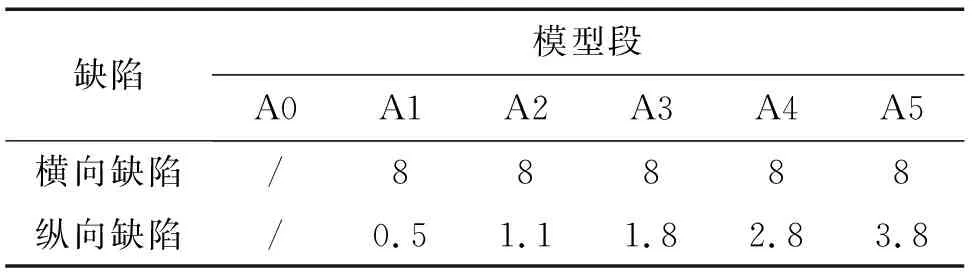
2.2 仿真信號分析



3 試驗測量與分析

4 結(jié)論

