用于粒子分離器的砂粒反彈特性實驗研究

李潔瓊，周 軍，王鎖芳

(1.上海航天設備制造總廠，上海 200245； 2. 南京航空航天大學 能源與動力學院，江蘇 南京 210016)

0 引言

粒子分離器對直升機發動機的進氣防護起著至關重要的作用，然而粒子分離器的形面較為復雜，其形面主要由砂粒與壁面的反彈性質決定，砂粒與壁面的碰撞所帶來的能量損失及內部流場擾動均會影響IPS的性能。如今對砂粒與不同材料的IPS壁面反彈特性未有一個統一的標準，故對砂粒的反彈特性展開實驗研究具有重要的實際意義。

國外較早開始研究砂粒反彈特性，文獻[1-3]早在17世紀后期便提出了經典剛體理論，說明簡單方式碰撞時的砂粒特性。該理論建立在推動力與動量關系的基礎上，忽略了碰撞過程中的瞬態力與砂粒滑移的影響。為分析砂粒與壁面的碰撞，已有相當多的實驗探究展開，為數值模擬提供了數據。文獻[4-5]運用激光多普勒風速風向測定法，對細小的玻璃微珠與塑性和彈性材料的碰撞展開探究。采用2種實驗臺探索低速與高速碰撞。分析砂粒入射角度與入射速度對法向恢復系數的影響發現，入射角度對于砂粒與硬板和軟板的碰撞的影響截然不同。文獻[6-7]運用光纖探頭測量砂粒的速度，通過玻璃微珠碰撞不同材料的平板，發現當入射角度很小時，法向反彈系數很小，且粗糙度對于法向反彈系數的影響很小；但是未研究砂粒單獨碰撞平板。

國內對于砂粒反彈特性的機理研究較少，文獻[8]設計并建立了測量砂粒侵蝕炭化層反彈系數的實驗系統，應用直徑為1.5 mm的砂粒從不同角度侵蝕炭化層，測得不同入射角時的法向及切向反彈系數。應用準牛頓優化算法，利用三次方多項式擬合實驗數據，得到法向反彈系數和切向反彈系數。文獻[9-10]理論研究了耗散砂粒動力學方法在流動問題中的應用，給出了耗散流體砂粒運動的控制方程組、邊界條件、數值方法及隨機數據統計方法等。用固壁砂粒層結合流體砂粒反彈運動的方法來處理固壁邊界有滑移流動邊界條件。

上述文獻均是針對砂粒反彈特性展開實驗研究，并采用了多種測速方法捕捉砂粒的運動軌跡，分析了壁面反彈系數的影響因素，但選取的實驗工況種類較少，局限于幾種壁面材料，未能很好地應用于粒子分離器結構設計中。因此，設計砂粒反彈實驗系統，拓展實驗工況，并將實驗結果應用于粒子分離器的設計工作中具有重要意義。

本文建立了砂粒反彈實驗臺，采用斜撞擊反彈模型研究砂粒反彈特性，分析對比不同材料、不同粒徑碰撞下的反彈系數，并將其擬合成多項式，為數值模擬粒子分離器內砂粒運動提供了可靠詳細的反彈系數，進而可精確地優化設計粒子分離器，提高粒子分離器的性能。

1 砂粒反彈模型

應用彈性理論中文獻[11-12]建立的斜撞擊反彈模型，理論分析球形顆粒與不同平板的反彈特性，了解砂粒在碰撞前后的受力、速度變化及能量變化。圖1為砂粒反彈前后速度矢量的示意圖。圖中：vi為砂粒入射速度；vr為砂粒反彈速度；θi為砂粒入射角(入射速度與法線的夾角)；vti，vni分別為入射速度vi的切向及法向分量；vtr，vnr分別為反彈速度vr的切向及法向分量；ωr為碰撞反彈后角速度；θr為砂粒反射角。

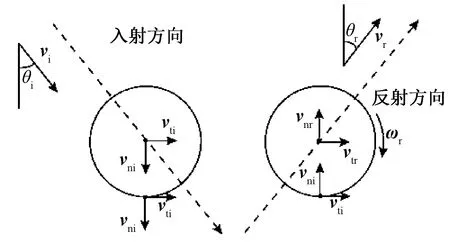
圖1 砂粒速度矢量示意圖Fig.1 Skematic diagram of particle velocity vector

有如下公式

(1)

(2)

vtr=Rωr

(3)

式中：vtr，vti，vnr，vni，vr，vi，ωr均為對應物理量的大小(下同)；R為砂粒半徑；et為切向反彈系數；en為法向反彈系數。

定義I為砂粒碰撞時的沖量，f為切向與法向的沖量大小之比。

(4)

式中：In，It分別為法向和切向沖量；Fn，Ft分別為碰撞時砂粒受到壁面的法向和切向力。滑移存在時，滿足

|Ft|=μ|Fn|

(5)

式中：μ為砂粒與固壁面之間的摩擦系數，μ=f。

動量定理(以法向與切向為正方向)為

In=m(vnr-vni)

(6)

It=m(vtr-vti)

(7)

動量矩定理為

Jα=∑M(Fi)

(8)

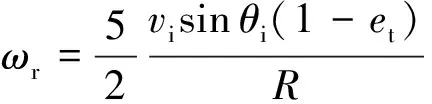
(9)

當砂粒與壁面發生碰撞發生滑移現象時，可得

et=1-μ(1+en)/tanθi

(10)

采用斜撞擊反彈模型時，通過測量砂粒的入射速度vi、入射角θi、反彈速度vr、反射角θr，即可得出砂粒反彈特性的變化規律。

2 實驗系統

圖2為整個砂粒反彈實驗系統的示意圖，包括投砂系統、砂粒反彈實驗箱、測試系統、砂塵回收系統等部分組成。

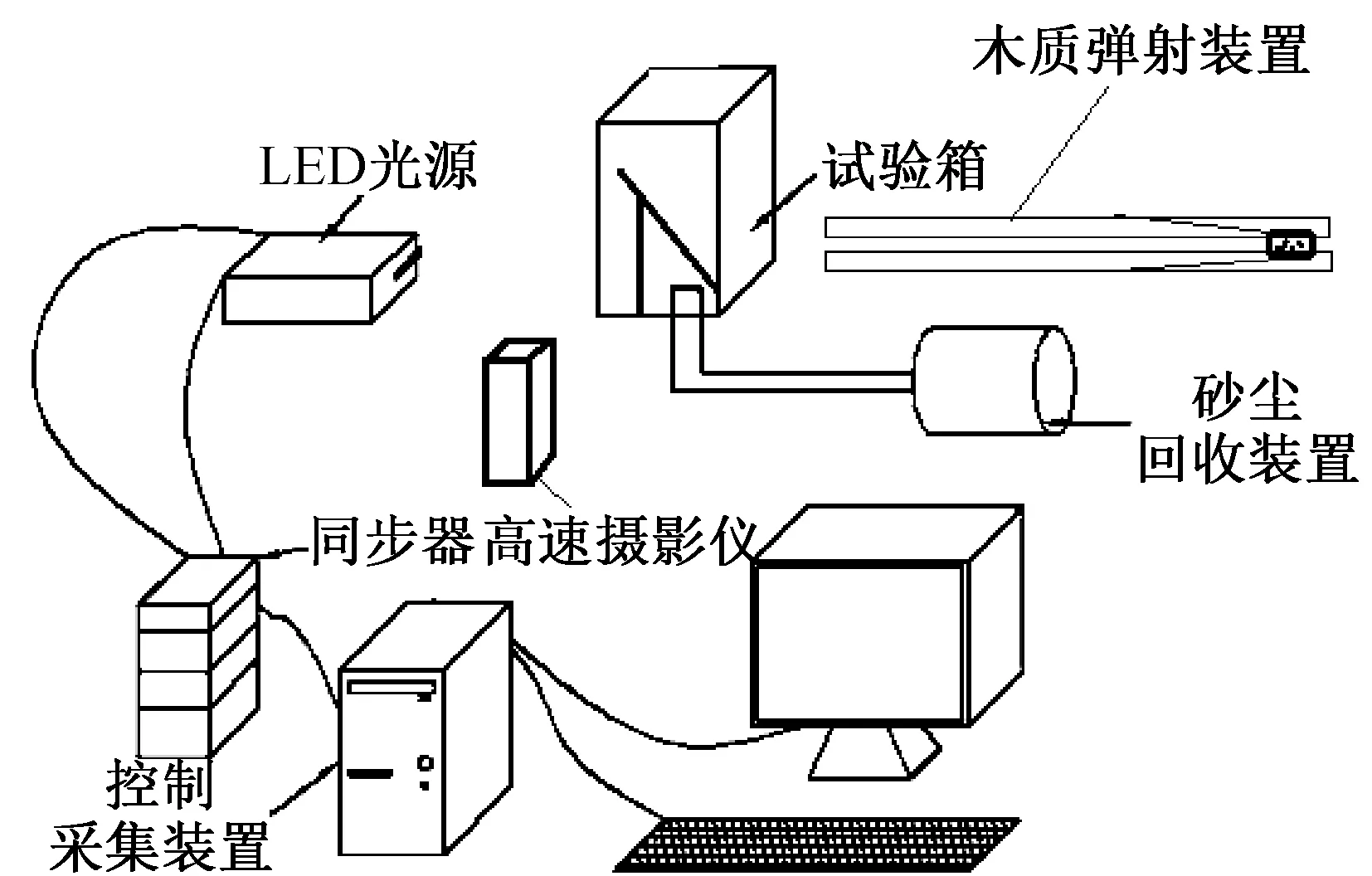
圖2 砂粒反彈實驗系統示意圖Fig.2 Schematic diagram of experimental system of particle rebound

投砂系統主要由木質軌道、木質彈頭以及彈性繩組成，其中彈頭與皮帶連接固定于軌道中，彈射原理是通過拉緊彈力繩使得裝有砂粒的彈頭具有一定的能量，松開彈力繩后彈頭在軌道中快速運動并在出口處被阻攔，而砂粒則射入實驗箱內，與實驗板發生反彈。實驗箱內包含碰撞平板、角度調節桿及安裝架。通過調整調節桿與安裝架，可改變平板的角度以及平板在實驗箱內的位置。為保證拍攝效果的清晰度，將實驗箱其中一個面噴上黑漆。同時為保證測試時具有良好的精度，拍攝部分換為光學玻璃。測試系統采用的高速攝影儀型號為Motion Pro Y5，鏡頭為Nikon 50 mm 1∶1.4D，最高拍攝速度為2 345 frame/s。調節高速攝影儀，將砂粒與實驗板的碰撞前后的運動過程以單幀圖片的形式儲存于計算機中，通過軟件處理得到砂粒反彈前后的速度矢量。

實驗中采用樹脂涂層、鋁以及高溫合金3種材料的實驗板，通過調整3種材料的實驗板與水平面的夾角，使得砂粒的入射角從 10°～90°均勻變化。實驗物料分別采用粒徑為350～500 μm的砂粒和粒徑為580～800 μm的砂粒，且砂粒的入射速度保持20 m/s，且砂粒均采用球形顆粒，從而排除砂粒形狀對壁面反彈系數的影響。

3 圖像處理方法

調整高速攝影儀的拍攝速度至2 000 frame/s，待砂粒裝入木質彈射裝置中拉緊彈射裝置中的皮帶，這時高速攝影儀開始錄制，直至砂粒與實驗板碰撞后錄制結束。圖3為實驗過程中其中一個砂粒的入射過程。圖4為實驗過程中其中一個砂粒的反射過程。

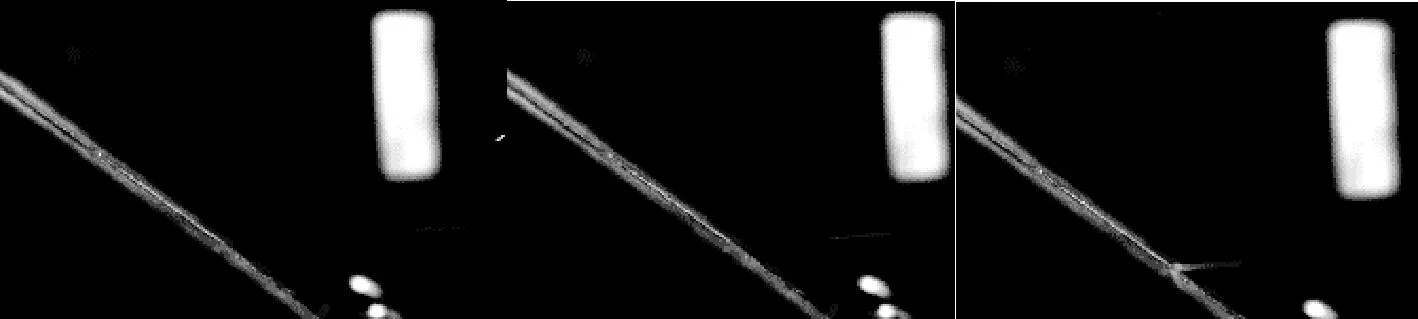
圖3 砂粒入射圖像Fig.3 Image of particle incident process

圖4 砂粒反射圖像Fig.4 Image of particle rebound process

圖3、4中的圖像疊加后即為砂粒的實際運動軌跡。其中每幀圖像間隔時間為0.5 ms，量取相鄰2幅圖片中砂粒所走距離及與圖像中白色標識的實際尺寸，比較可得砂粒的入射速度與反彈速度。測量圖中砂粒軌跡與實驗板角度，即可算出砂粒的法向與切向反彈系數。實驗過程中，因砂粒與壁面碰撞的結果存在隨機性，且砂粒的入射情況也是概率分布的，為減小實驗誤差，下文圖中每個點代表保持入射速度與入射角度不變時，除去偏差較大的實驗結果，統計20次實驗結果的平均值。

4 實驗數據分析

4.1 彈性碰撞下反彈系數的變化

因樹脂材料板面彈性較好，砂粒與樹脂壁面的碰撞為彈性碰撞。圖5為砂粒與樹脂板碰撞時的切向反彈系數隨著入射角度的變化關系，其中橫坐標為入射角度的弧度值。

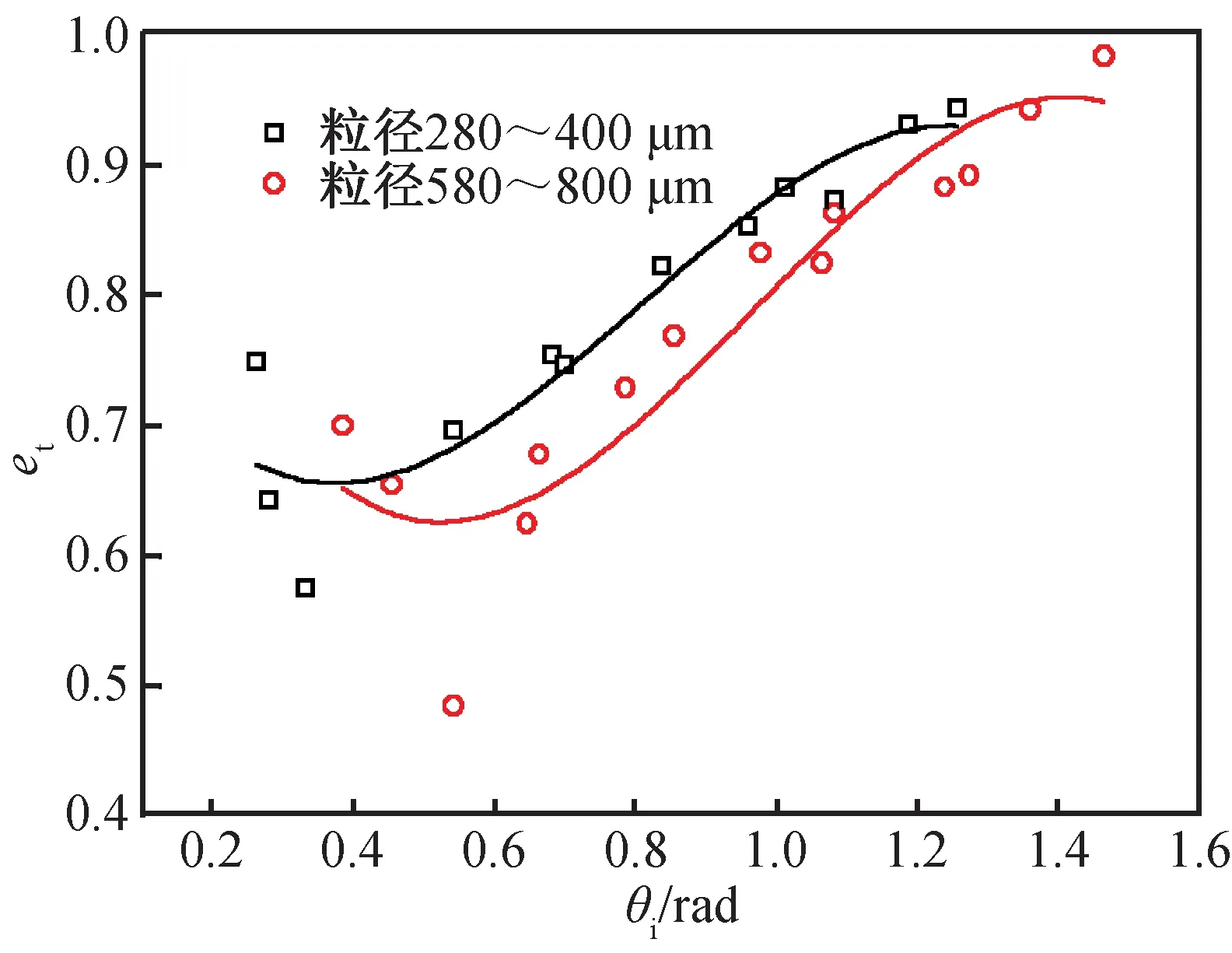
圖5 彈性碰撞下切向反彈系數隨著入射角度的變化Fig.5 Tangential restitution coefficient changing with incident angle under elastic collision

根據實驗點的分布擬合成多項式曲線，由圖5中擬合曲線可看出，對于彈性碰撞，壁面的切向反彈系數隨著入射角度的增大而呈增大的趨勢。 對于粒徑為280～400 μm的砂粒，當入射角度為0.2 rad時，切向反彈系數接近于0.6，隨著入射角度增大至1.4 rad時，切向反彈系數增大至0.9。當粒徑為580～800 μm時，切向反彈系數隨著入射角度的變化趨勢雖與粒徑較小時保持一致，但當入射角度較小或較大時，切向反彈系數的變化較為平緩，甚至趨于相反。其主要原因是：在入射速度不變的情況下，入射角度越小，與壁面的碰撞程度越強烈，因而能量消耗較大；切向反彈系數受砂粒滑移的影響，即與壁面的摩擦系數等特性有關，入射角度較小時，法向入射速度較大，產生的摩擦力較大，能量損失也較大。根據圖中擬合曲線可得樹脂材料的切向反彈系數的多項式為

ets(280-400)= 0.785+0.975αi-

1.89(αi)2+0.828(αi)3

(11)

ets(580-800)=0.918+0.458αi-

1.67(αi)2+0.924(αi)3

(12)

砂粒與樹脂板碰撞時的法向反彈系數隨著入射角度的變化關系如圖6所示，橫坐標為入射角度的弧度值，且圖中每個點代表保持入射速度與入射角度不變的多次實驗結果的平均值。

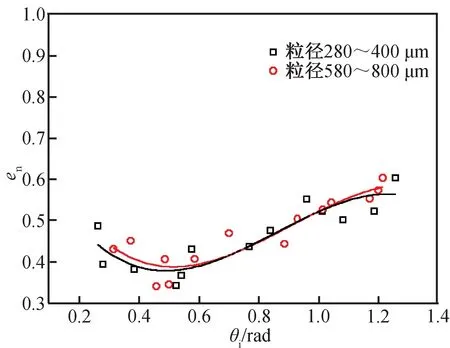
圖6 彈性碰撞下法向反彈系數隨著入射角度的變化Fig.6 Normal restitution coefficient changing with incident angle under elastic collision

從圖6中可看出，對于粒徑為280～400 μm的砂粒，隨著入射角度由0.2 rad增大至1.3 rad，法向反彈系數由0.4平緩增大至0.6；而對于粒徑為580～800 μm的砂粒，隨著入射角度的增大，法向反彈系數的變化趨勢相同。故對于樹脂材料板，砂粒的法向反彈系數受到入射角度的影響較小。其原因是：因砂粒與樹脂壁面的碰撞為彈性碰撞，即壁面變形消耗的能量很少，砂粒在碰撞時產生的旋轉動能與平移動能消耗較多。根據圖中擬合曲線可得樹脂材料的法向反彈系數的多項式為

ens(280-400)= 0.41+1.008αi-

1.94(αi)2+0.91(αi)3

(13)

ens(580-800)= 0.499+0.71αi-

1.64(αi)2+0.826(αi)3

(14)

4.2 彈性碰撞下旋轉角速度的變化關系

由式(9)可看出，砂粒入射時的旋轉角速度隨著砂粒的入射角度及切向反彈系數的變化而變化。圖7為2種粒徑的砂粒在彈性碰撞下的旋轉角速度與入射角度的變化關系。橫坐標為砂粒的入射角度，縱坐標為砂粒的旋轉角速度。

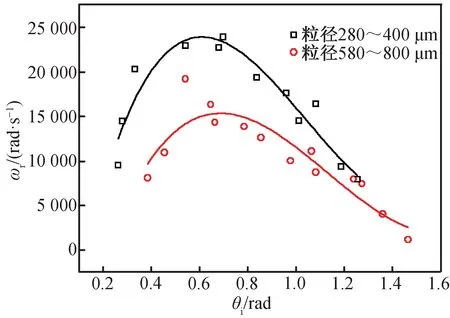
圖7 彈性碰撞下旋轉角速度隨著入射角度的變化Fig.7 Rotation speed changing with incident angle under elastic collision

從圖7中擬合曲線可看出，對于粒徑為280～400 μm的砂粒，隨著入射角度的增大，旋轉角速度的變化平緩，且在入射角度達到25°時，砂粒的旋轉速度達到最大；隨著入射角度繼續增大，旋轉角速度隨之緩慢減小。而對于粒徑為580～800 μm的砂粒，則隨著入射角的增大，旋轉角速度先增大后減小，在入射角為35°時達到最大值。對比圖中2條擬合曲線可知，粒徑較小的砂粒的旋轉角速度的變化較粒徑較大的砂粒平緩，且當入射角大于65°時，2種粒徑的旋轉角速度差值逐漸增大。說明粒徑不同，砂粒的旋轉角速度受到入射角度的影響也不同。

4.3 非彈性碰撞下反彈系數的變化

鋁板與合金鋼板的硬度較大，不易產生彈塑性變形，故砂粒與鋁板、合金剛板之間為非彈性碰撞。圖8為砂粒與鋁板、合金鋼板碰撞時切向反彈系數隨著入射角度的變化關系。橫坐標為砂粒入射角度的弧度值，縱坐標為切向反彈系數，圖中的實驗點均為多次重復實驗所取的平均值。

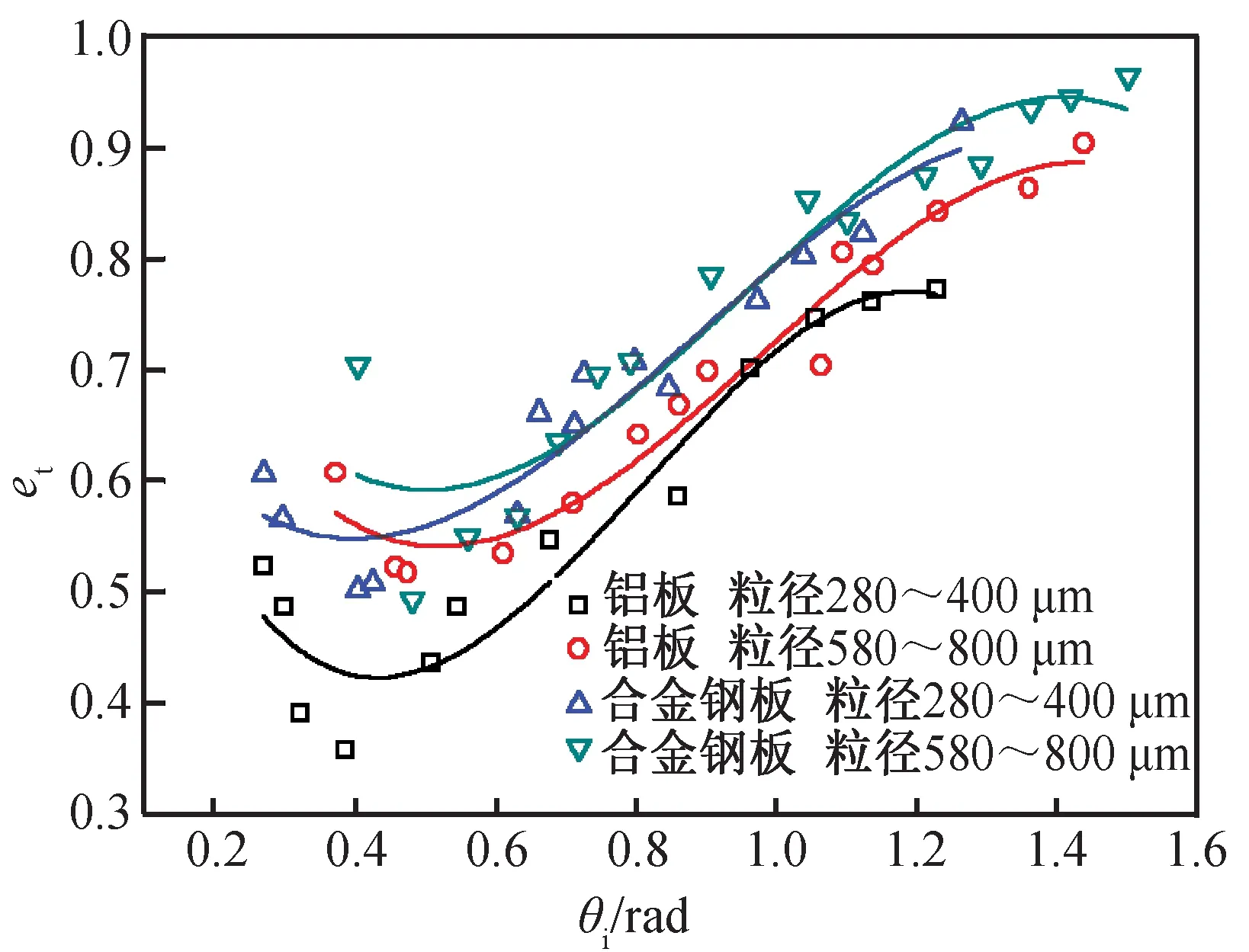
圖8 非彈性碰撞下切向反彈系數隨著入射角度的變化Fig.8 Tangential restitution coefficient changing with incident angle under plastic collision

從圖8中可見，鋁板在2種粒徑的砂粒的碰撞下，其切向反彈系數隨著砂粒入射角度的增大而增大。在入射角度相同的情況下，當粒徑較小的砂粒碰撞鋁板時，切向反彈系數較大。同時，當入射角度較小時，粒徑對于壁面切向反彈系數的變化影響較小，隨著入射角度的增大，小粒徑的壁面法向反彈系數較大粒徑明顯增大，且增大的趨勢也更為劇烈，由此可知，粒徑越大的砂粒與壁面碰撞，旋轉動能與壁面變形消耗的能量越多，反彈系數較小。根據圖中擬合曲線可得鋁板的切向反彈系數的多項式公式為

etl(280-400)= 0.413 68+2.098 93αi-

3.655 1(αi)2+1.597 88(αi)3

(15)

etl(580-800)= 0.863 13+0.381 21αi-

1.595 5(αi)2+0.896 23(αi)3

(16)

對于合金鋼板，當入射角度為0.45 rad左右時，粒徑為280～400 μm的砂粒碰撞時，切向反彈系數達到最小值為0.62，隨著入射角度的增大至1.2 rad時，切向反彈系數達到最大值0.85；而對于粒徑為580～800 μm的砂粒碰撞時，切向反彈系數達到最小值為0.52，且在入射角度為1.4 rad時達到最大值為0.95。即粒徑較大的砂粒碰撞合金鋼板時，切向反彈系數較粒徑較小的砂粒碰撞要大。同時從圖中可看出，非彈性碰撞下的切向反彈系數的變化趨勢與彈性碰撞下切向反彈系數的變化趨勢相似。根據圖中擬合曲線可得合金鋼板的切向反彈系數的多項式公式為

eth(280-400)=0.855 53+0.570 53αi-

1.637 9(αi)2+0.791 63(αi)3

(17)

eth(580-800)=0.908 43+0.490 43αi-

1.743 7(αi)2+0.943 4(αi)3

(18)

非彈性碰撞下法向反彈系數隨著砂粒入射角度的變化關系如圖9所示。其中橫坐標為砂粒入射角度的弧度值，縱坐標為切向反彈系數，圖中的實驗點仍為多次重復實驗所取的平均值。

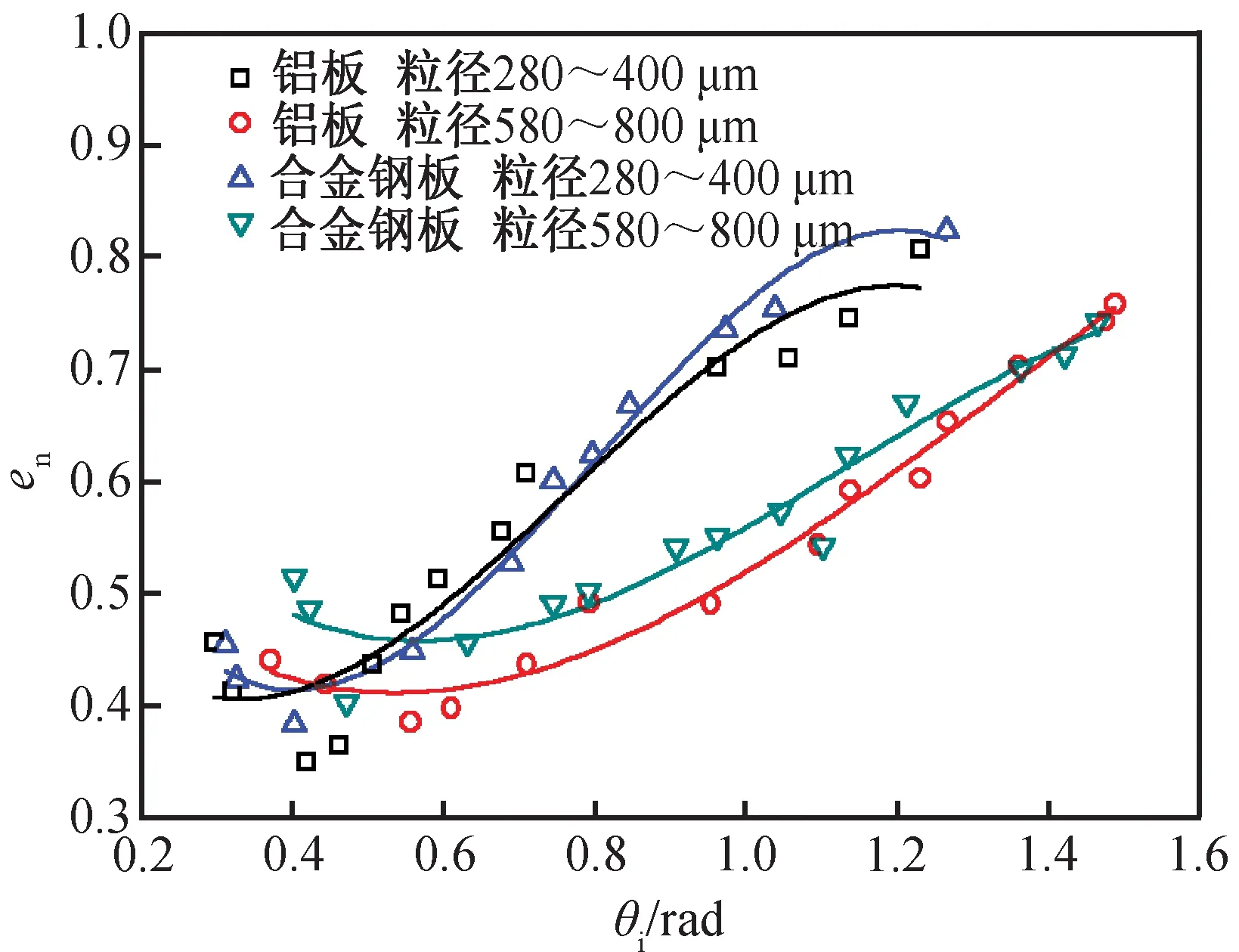
圖9 非彈性碰撞下法向反彈系數隨著入射角度的變化Fig.9 Normal restitution coefficient changing with incident under plastic collision

從圖9可見，非彈性碰撞下法向反彈系數隨著砂粒入射角度的變化與彈性碰撞下的變化不同，隨著入射角度的增大，2種材料的法向反彈系數均隨之增大。對于合金鋼板較鋁板，其法向反彈系數的變化更為平緩，說明非彈性變形起到一定的消耗作用。同時鋼板表面因碰撞而產生的塑性變形(缺口、壓痕等)也會影響到砂粒與板面的反彈特性。當入射角度較小時，粒徑對于壁面法向反彈系數的變化影響較小，隨著入射角度增大，小粒徑的壁面法向反彈系數較大粒徑明顯增大，且增大的趨勢也更為劇烈，由此可得，粒徑越大的砂粒與壁面碰撞，旋轉動能與壁面變形消耗的能量越多，反彈系數較小。根據圖中擬合曲線可得2種材料的法向反彈系數的多項式公式為

enl(280-400)=0.508 81+1.582 84αi-

2.752 64(αi)2+1.136 5(αi)3

(19)

enl(580-800)=0.795 94-0.470 9αi-

0.167 4(αi)2+0.254 7(αi)3

(20)

enh(280-400)=0.478 81+2.084 79(α)i-

3.704 31(αi)2+1.602 85(αi)3

(21)

enh(580-800)=0.757 84-0.161 74αi-

0.573 89(αi)2+0.435 7(αi)3

(22)

4.4 非彈性碰撞下旋轉角速度的變化關系

因砂粒碰撞時的角速度與切向反彈系數有關，故板面的硬度對砂粒的角速度也有影響。圖10為非彈性碰撞下砂粒碰撞時的角速度與入射角度的關系。其中橫坐標為砂粒的入射速度，縱坐標為砂粒的旋轉角速度。

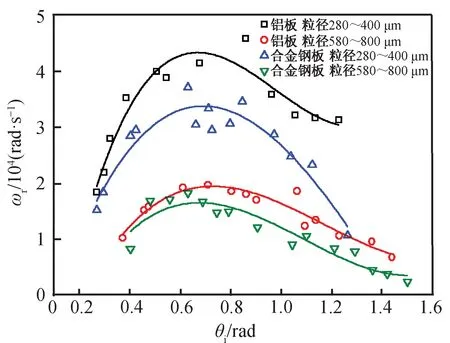
圖10 非彈性碰撞下旋轉角速度隨著入射角度的變化Fig.10 Rotation speed changing with incident angle under plastic collision

從圖10中可見，當砂粒粒徑較小時，砂粒的角速度隨著入射角度的變化較為劇烈，均呈先增大后減小的趨勢；而對于粒徑較大的砂粒，砂粒的旋轉角速度隨著入射角度的變化較為平緩，且較粒徑較小的砂粒的旋轉角速度平均減小20.22%。在鋁板與合金鋼板碰撞下，砂粒角速度較為接近，但當砂粒的入射角度為35°時， 與合金鋼板碰撞的砂粒的旋轉角速度達到最大值，而與鋁板碰撞的砂粒在入射角度為55°時才達到最大值。與圖7比較可知，因2種材料碰撞下的切向反彈系數較為接近，故對于非彈性碰撞，砂粒的旋轉角速度受砂粒粒徑的影響較大，受板面材料的影響相對較小。

5 結論

基于自行搭建的砂粒反彈特性測試實驗臺，采用2種粒徑的砂粒碰撞3種不同材料的實驗板，利用高速攝影儀測量砂粒的運動軌跡及運動參數，通過對比不同材料與不同粒徑下反彈系數的變化來分析砂粒反彈特性的影響因素，實驗結果表明：

1) 彈性碰撞下，壁面的切向反彈系數隨著入射角度的增大而增大。當入射角度不變時，粒徑為280～400 μm的砂粒碰撞時較粒徑為580～800 μm的砂粒碰撞，切向反彈系數大。壁面的法向反彈系數隨著入射角度的增大而變化平緩。入射角度不變時，粒徑較小的砂粒碰撞時與粒徑較大的砂粒碰撞時的法向反彈系數接近。

2) 彈性碰撞下，粒徑為280～400 μm的砂粒的角速度隨著入射角度的增大，先增大后減小，且在入射角度為0.6 rad時達到最大值；粒徑為580～800 μm的砂粒的角速度隨著入射角度的增大，先增大后緩慢減小，且在入射角度為0.7 rad時達到最大值。

3) 非彈性碰撞時，鋁板與合金鋼板在2種粒徑的砂粒的碰撞下，其切向反彈系數隨著砂粒入射角度的增大而增大，且粒徑較大的砂粒碰撞合金鋼板時，切向反彈系數大于粒徑較小的砂粒碰撞時的切向反彈系數。相同粒徑的砂粒碰撞時，合金鋼板的切向反彈系數大于鋁板的切向反彈系數。

4) 非彈性碰撞下法向反彈系數隨著砂粒入射角度的變化與彈性碰撞下的變化相似，隨著入射角度的增大，2種材料的法向反彈系數均隨之增大。當入射角度較小時，粒徑對于壁面法向反彈系數的變化影響較小，隨著入射角度增大，小粒徑的壁面法向反彈系數較大粒徑的壁面法向反彈系數明顯增大。

5) 當砂粒粒徑較小時，砂粒的角速度隨著入射角度的變化較為劇烈，均呈先增大后減小的趨勢；而對于粒徑較大的砂粒，砂粒的旋轉角速度隨著入射角度的變化較為平緩。粒徑相同的砂粒碰撞鋁板與合金鋼板時，砂粒角速度較為接近，但當砂粒的入射角度為0.7 rad時，鋁板與合金鋼板碰撞的砂粒的旋轉角速度達到最大值。

目前，對于不同粒徑的砂粒與不同材料的粒子分離器壁面的反彈特性，國內外一直未有通用的模型和參數，不同壁面因反彈系數不同，砂粒運動存在差異性，對粒子分離器型面的影響不同，是粒子分離器設計的瓶頸。為此，設計了砂粒反彈實驗系統，研究了砂粒的反彈特性，但未研究較小粒徑的砂粒。后續的工作需采用更高拍攝速度的高速攝影儀獲取砂粒的運動軌跡，研究砂粒的形狀、材料等參數對于砂粒反彈特性的影響，進一步探索實驗板的硬度、楊氏模量等參數對于反彈系數的影響。

[1] GOLDSMITH W, FRASIER J T. Impact: the theory and physical behavior of colliding solids [J]. Journal of Applied Mechanics, 1961, 28(4): 631-639.

[2] STRONGE W J. Rigid body collisions with friction[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1990: 169-181.

[3] STRONGE W J. Impact mechanics[M]. England: Cambridge University Press, 2004.

[4] MARTIN S R， PINFOLD T M，WALLACE S G R.Applications of laser techniques to fluid mechanics[M].Berlin:Springer, 1991：125-141.

[5] SOMMERFELD M, HUBER N. Experimental analysis and modelling of particle-wall collisions [J]. International Journal of Multiphase Flow, 1999, 25(6): 1457-1489.

[6] FRANK T, SCHADE K P, PETRAK D. Numerical simulation and experimental investigation of a gas-solid two-phase flow in a horizontal channel [J]. International Journal of Multiphase Flow, 1993, 19(1): 187-198.

[7] LUN C K K, LIU H S. Numerical simulation of dilute turbulent gas-solid flows in horizontal channels[J]. International Journal of Multiphase Flow, 1997, 23(3): 575-605.

[8] 徐義華, 張燕海, 楊玉新, 等. 粒子侵蝕模型及砂粒侵蝕下絕熱材料燒蝕數值計算[J]. 固體火箭技術, 2015, 38(1): 37-44.

[9] 孔軼華, 張楚華, 席光. 耗散粒子動力學在流動數值模擬中的應用[J]. 西安交通大學學報, 2006, 40(9): 1104-1108.

[10] 孔軼華, 張楚華, 席光, 等. 耗散粒子動力學對顆粒沉降問題的研究[J]. 工程熱物理學報, 2008(1): 59-61.

[11] MAW N, BARBER J R, FAWCETT J N. The oblique impact of elastic spheres [J]. Wear, 1976, 38(1): 101-114.

[12] MAW N, BARBER J R, FAWCETT J N. The role of elastic tangential compliance in oblique impact [J]. Journal of Tribology, 1981, 103(1): 74-80.