基于MIMU的輸電線路振動分析

楊金顯， 楊 闖， 李雙磊， 蔣志濤， 王鵬飛(.河南理工大學 電氣工程與自動化學院，河南 焦作 454003；.國網山東臨朐縣供電公司，山東 臨朐 6600)

輸電線路是輸電的紐帶，特別是特高壓輸電線路，保證其安全運行至關重要，尤其在特高壓輸電工程所采用的導線截面、懸掛點高度以及檔距都有所增大，其風致振動非常嚴重。按頻率和振幅劃分，主要為高頻微幅的微風振動、中頻中幅的次檔距振蕩和低頻大振幅的舞動[1]，三種振動都會給輸電線路造成破壞，容易引起導線疲勞斷股、金具損壞、相間閃絡，造成線路跳閘停電或引起燒傷或折斷導線，桿塔倒塌等嚴重事故，嚴重影響特高壓輸電線路的安全運行，需要設計阻尼控制器減緩輸電線路的振動。阻尼控制器的設計與輸電線路振動幅度和頻率直接相關，不同地區輸電線路振動幅度和頻率不同，阻尼器的設計參數也不同，為最大程度發揮阻尼器性能，必須結合本地區長期輸電線路振動特性，因此對輸電線路振動幅度和頻率的分析就變的至關重要。

近年來，基于MEMS加速度計/陀螺儀的微慣性姿態測量單元(MIMU)以其成本低、體積小、壽命長、集成化、抗沖擊能力強和可靠性高等優勢，發展迅猛，應用廣泛，可進行輸電線振動信息的檢測，引起了諸多研究人員關注：張帆等[2-3]最初采用MEMS加速度計多點監測輸電線振動加速度，忽略輸電線扭轉影響通過積分解算輸電線運動軌跡等參數；王有元等[4]通過重新標定積分基線以抑制因加速度積分產生的軌跡發散，利用加速度分解合成關系推導轉換公式以消除傳感器扭轉引起的誤差；黃新波等[5]為避免導線舞動扭轉導致計算出的相對位移與實際運動偏差，設計了基于MIMU和ZigBee無線組網的導線舞動多點監測系統；邵穎彪等[6]為克服傳統只用加速度計監測導線舞動只能得到位移的缺陷，設計了基于MIMU/磁強計的輸電導線姿態解算多點監測方案。上述這些裝置或方法采用慣性測量來實現導線的定位，計算軌跡(姿態和位置)，進而獲取輸電線路風致振動幅度和頻率，難度十分巨大，能夠實現這些功能需要導航級慣性導航系統，體積和成本都會很大，另外慣性測量存在需要初始值和隨著時間的積累誤差會越來越大的缺點，會導致最后無法測量，不能長期計算導線振動幅度和頻率。由于特高壓導線周圍有強磁場干擾加上輸電導線安裝監測節點困難，通過ZigBee等無線組網將檔距內多個MIMU或MIMU/磁強計監測節點互聯的多點監測方案很難實施。

從振動成分來看，任何復雜振動都是由不同振動成分組成的，關鍵找出振動的主要部分——幾種基本的模式振動分量。盡管輸電線路振動包括各種復雜的運動(幅度和頻率都會發生變化)，但其基本模式是平動和扭轉[7]，因此可通過對輸電線路平動和扭轉分析以了解其振動特性(振幅和頻率)。輸電線路在絕緣子串懸掛點受力情況最為復雜，最易因輸電線路振動發生故障，更重要的是懸掛點包含更多輸電線路振動信息，輸電線路正常運行時，懸掛點振動角一般在30′～50′，導線振動幅度越大，振動角越大，導線舞動時，振動角接近10°，另外在該處安裝監測設備也容易實現，因此，可通過采集此處平動和扭轉信息，來計算輸電線路振動幅度和頻率[8-11]。

懸掛點采集的平動和扭轉信號較弱，極易受周圍磁場干擾，鑒于此，設計一種MIMU測量節點，并采用一定長度的彈性桿進行信號物理放大和防電磁干擾，為提高系統精度，實現長期監測輸電線路振動幅度和頻率，不利用加速度和角速度的解算信息，而直接通過監測加速度時間序列的二階矩來計算數據的變異度，預測輸電線路平動及扭轉的幅度；通過對監測數據的相似性分析，預測輸電線路平動及扭轉的頻率；最后設計了振動臺、轉臺試驗和輸電線路模型模擬實驗，實驗結果表明處理數據結果能夠反映輸電線路振動變化規律，說明輸電線路振動分析方法是有效的，可以為輸電線路的運動阻尼控制參數計算提供參考。

1 MIMU數據采集與處理

1.1 MIMU測量系統

MIMU作為輸電線運動監測節點通過延長桿固連于桿塔絕緣子串懸掛點處，如圖1所示，延長桿的使用一是為了監測節點和導線有一定的距離，減小電磁干擾；二是為了增大觀測能力，由于實際的監測節點不能安裝在導線上(特高壓導線強磁干擾，且安裝困難)，但又不能降低監測的能力，為了增大觀測能力，采用具有一定彈性、一定長度的桿。彈性桿長度滿足共振的范圍要求，使輸電導線振動時滿足振幅最大，最大程度的敏感振動幅度、頻率及變化趨勢，由于輸電導線振動頻率較小且是變化的，不會使彈性桿振壞。MIMU采集的數據經光纖傳至桿塔處理器進行后續數據處理，為減少輸電線路電磁場干擾，桿塔處理器通過剛性桿向空中延伸。

圖1 輸電線路模型及MIMU布置圖Fig.1 Transmission lines model and MIMU layout

1.2 MIMU數據AR-Kalman濾波處理

由于MIMU加速度計讀數為合加速度A，包含振動加速度a，重力加速度g和測量噪聲ε，進行平動和扭轉分析需提取振動加速度(平動方向，即水平和垂直方向，下同)和重力加速度。MIMU振動加速度及重力加速度通過MIMU角速度信息輔助提取[12-13]，通過AR-Kalman對其進一步降噪。

對MIMU加速度信號(振動、重力加速度)建立時間序列模型時，須對提取的振動、重力加速度數據預處理，使其滿足平穩隨機序列，以對其建立時序模型。本文綜合考慮AIC準則、模型適用性和系統實時性要求，選用AR(2)模型分別對提取的運動加速度a和重力加速度g進行建模[14-15]，根據觀測量at(振動加速度)、gt(重力加速度)，通過最小二乘法擬合自回歸參數α1、α2、β1、β2，分別得其AR(2)模型

at=α1at-1+α2at-2+εat

gt=β1gt-1+β2gt-2+εgt

建立輸電線路加速度AR(2)模型后，采用Kalman濾波進一步降噪提高信號精度，狀態方程為

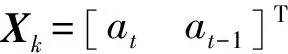
將上述狀態參數帶入Kalman濾波公式計算運動加速度最優濾波值[16](重力加速度處理流程相同)。

2 輸電線路振動分析

2.1 輸電線路平動特征提取

輸電線路平動時，會出現X,Y,Z三個軸的平動，如圖2所示，平動幅度與輸電線路所受外界合沖擊加速度有關，沖擊加速度越大，平動幅度越大，平動幅度近似正比于輸電線路振動加速度a，因此輸電線路的平動必然會引起振動加速度監測數據的變化，選取振動加速度信號時間序列作為平動特征量，記為ak，為消除偶然誤差同時壓縮數據量，對其進行滑動分段模式表示。將AR-Kalman濾波處理的振動加速度數據每L個為一組，每滑動l個數取一次平均，第i段記為ai(ai1,ai2,ai3,…,aiN)，其中N=L/l，ain為

(1)

圖2 輸電線平動示意圖Fig.2 Transmission line translational movement

將輸電線路靜止條件下振動加速度數據作為初始時間序列數據段，初始序列段均值記為a0。加速度數據每次變化的大小和這些變化的方向及持續時間，表示輸電線路所受外界沖擊力情況，也即平動幅度變化情況(沖擊力越大平動幅度越大)，通過計算ai相對a0二階中心距Dai0，獲取振動加速度數據變異情況，進而根據變異情況預測輸電線路平動幅度，Dai0為

(2)

振動加速度數據變化頻率也即輸電線路振動頻率。通過計算ai與ai+1歐式距離Daii+1，度量相鄰兩段序列的相似性，以測度振動加速度數據變異速率，進而根據變異速率判斷輸電線路平動頻率(歐式距離越大，相鄰兩序列段數據相似性越低，運動加速度數據變異越大，相鄰兩段數據序列變化越快，輸電線路平動加速度頻率越大)，Daii+1為

(3)

為便于預測平動幅度及頻率，將Dai0、Daii+1進行歸一化處理，分別記為Da(表示平動程度)、Fa(平動頻率系數)，即

Da=Dai0/Damax+ε1

(4)

Fa=Daii+1/DEamax+ε2

(5)

式中:Damax為設定的輸電線路最大運動加速度二階中心距，DEamax為設定的輸電線路相鄰運動加速度序列段最大歐式距離，ε為誤差因子。

2.2 輸電線路扭轉特征提取

沿輸電導線軸向觀察圖2，未發生或輕微扭轉時，重力加速度分量主要集中在Z軸，此時加速度計X軸敏感的重力加速度為0或約為0，如圖3(a)所示；發生扭轉運動時，Z軸向敏感的重力加速度分量會轉移或部分轉移給X軸，即扭轉運動時Z軸和X軸發生交叉耦合運動。Z軸向X軸轉移的重力加速度分量越多也即Z軸重力加速度分量越小，X軸重力加速度分量越大，說明輸電導線扭轉程度越大，如圖3(b)所示。因此輸電線路的扭轉必然會引起X軸Z軸重力加速度監測數據的變化，選取X軸Z軸重力加速度增廣信號[X,Z]時間序列作為扭轉特征量，記為gk(X,Z)，為消除偶然誤差同時壓縮數據量，對其進行滑動分段模式表示。將AR-Kalman濾波處理的X軸Z軸重力加速度數據每L個為一組，每滑動l個數取一次平均，第i段記為:gi(gi1,gi2,gi3,…,giN)，其中N=L/l，gin為

(6)

將輸電線路靜止條件下重力加速度數據作為初始時間序列數據段，初始序列段均值記為g0。重力加速度數據每次變化的大小和這些變化的方向及持續時間，表示輸電線路扭轉程度，通過計算gi相對g0二階中心距Dgi0，獲取重力加速度數據變異情況，進而根據變異情況預測輸電線路扭轉程度，Dgi0為

(7)

重力加速度數據變化頻率也即輸電線路扭轉的頻率。通過計算gi與gi+1歐式距離Dgii+1，度量相鄰兩段序列的相似性，以測度重力加速度數據變異速率，進而根據變異速率判斷輸電線路扭轉頻率，Dgii+1如下

(8)

把Dgi0、Dgii+1進行歸一化處理，分別記為Dg(扭轉程度)、Fg(扭轉頻率系數)，即

Dg=Dgi0/Dgmax+ε3

(9)

Fg=Dgii+1/DEgmax+ε4

(10)

其中Dgmax為設定的輸電線路最大增廣重力加速度二階中心距，DEgmax為設定的相鄰增廣重力加速度序列段最大歐式距離，ε為誤差因子。

(a) 未扭轉

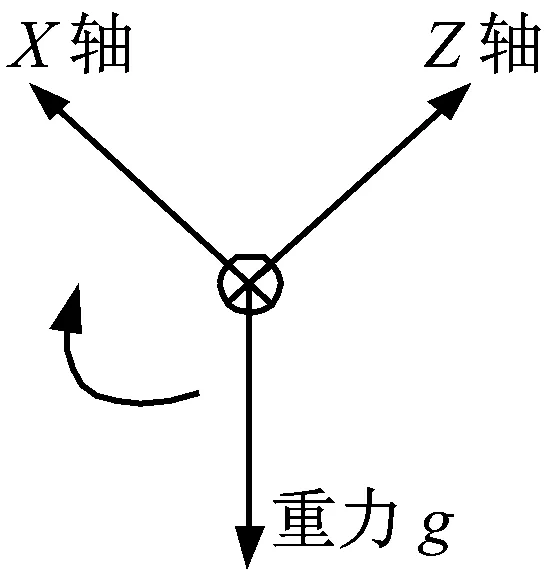
(b) 扭轉圖3 輸電線扭轉示意圖Fig.3 Transmission line torsional movement

2.3 輸電線路振動分析

綜上分析，輸電線路平動、扭轉分析流程如圖4所示，通過對連續采集的運動加速度、重力加速度變異度、相似性分析，計算振動幅度和頻率系數(系數越大，說明振動幅度、頻率越大)。

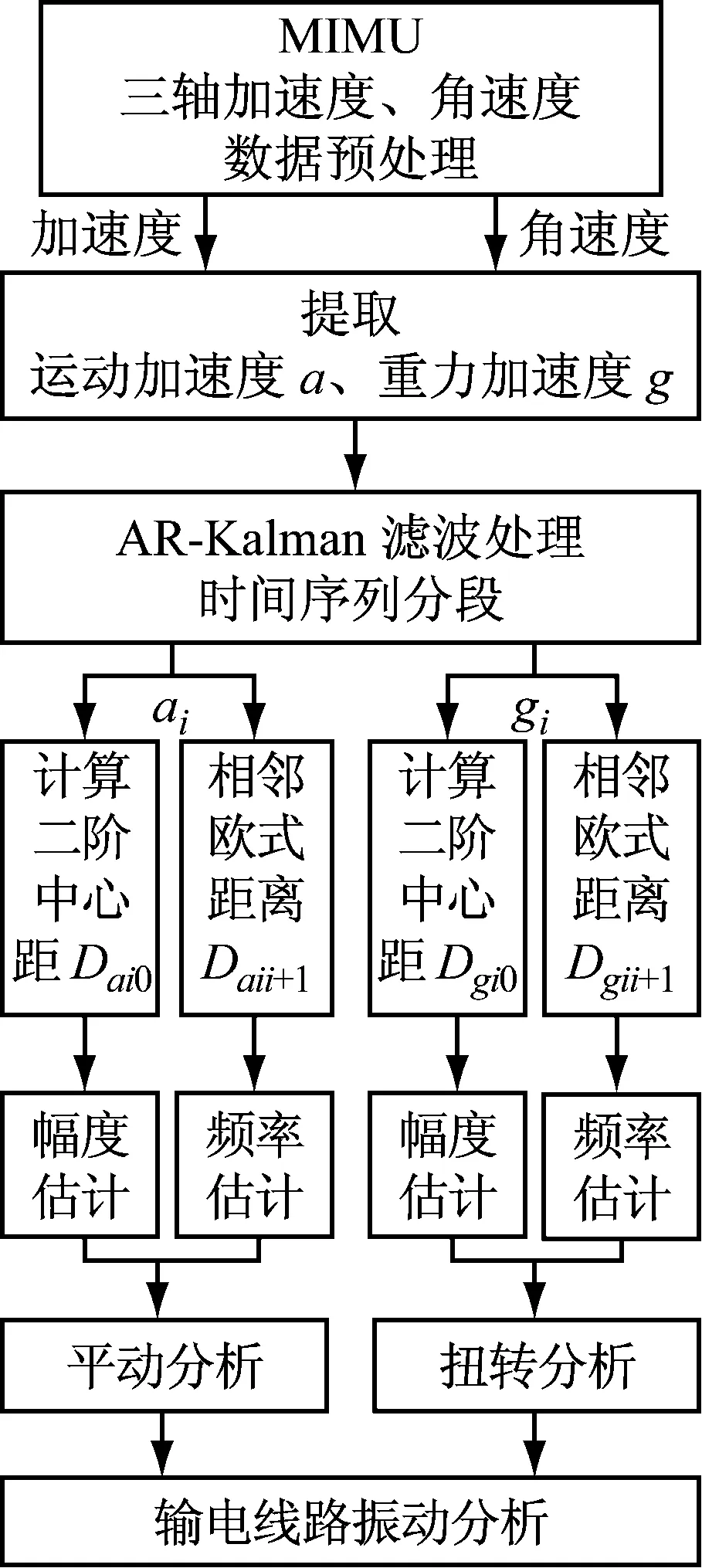
圖4 輸電線路振動分析流程圖Fig.4 Analysis process of transmission line vibration

由前文分析知，振動幅度和頻率系數的計算，依賴Damax、DEamax、Dgmax、DEgmax四個參數的確定。實際應用中，此四個參數的確定方法如下：①獲取本地區輸電線最大允許(或統計最大)平動或扭轉頻率，分別記為fa,fg；本地區輸電線最大允許(或統計最大)振動角記為θ，最大平動振幅A=d·tan(θ)(d為MIMU安裝點到絕緣子串懸掛點距離)；②振動臺以振幅A，頻率fa振動時采集MIMU加速度及角速度數據;搖擺臺以頻率fg，搖擺角θ搖擺運動時采集MIMU加速度及角速度數據；③通過前述流程計算相應的Dai0,Daii+1,Dgi0,Dgii+1多次重復上述過程，分別取Dai0,Daii+1,Dgi0,Dgii+1對應的均值作為Damax,DEamax,Dgmax,DEgmax。

以平動頻率系數為橫坐標、平動程度為縱坐標作幅頻系數圖，對應點稱為平動點；以扭轉頻率系數為橫坐標、扭轉程度為縱坐標作幅-頻系數圖，對應點稱為扭轉點，通過分析本地區平動點、扭轉點分布區域獲取本地區輸電線路振動特性，為后續振動阻尼器設計提供參數。

3 實驗設計及結果分析

3.1 振動臺模擬試驗

為驗證輸電線路平動分析方法性能，特設計振動臺振動模擬輸電線路平動試驗，將實驗室設計的MIMU系統固定在振動臺上，如圖5所示。考慮安裝及MIMU初始零偏誤差，振動臺靜止時采集MIMU振動加速度作為初始數據段，振動臺以不同振幅、頻率振動時采集MIMU運動加速度作為振動數據段，Damax、DEamax分別設為振動臺振幅/頻率5 mm/150 Hz對應的振動加速度二階中心距、相鄰序列段歐式距離，數據分段數l取為30，經2.1節平動分析流程估計MIMU平動幅度及頻率系數。

圖5 MIMU振動試驗Fig.5 Shaking-table test of MIMU

表1為振動臺振動時設定的“振幅/頻率”與由上述平動分析方法得到的平動“振幅系數/頻率系數” 平均估計結果對比。由表1知，當振幅分別設定為1 mm、3 mm、5 mm時，計算的平動程度Da分別落在(0.17,0.21)、(0.59,0.62)、(0.92,1)區域，振幅與平動程度近似線性關系，可見本文方法計算的平動幅度系數對設定輸入振幅有較好的跟隨性；當振動臺的輸入頻率依次為50 Hz、100 Hz、150 Hz時，計算的頻率系數Fa依次屬于(0.31,0.34)、(0.66,0.69)、(0.96,1)，頻率系數與輸入頻率近似線性關系，可見基于歐氏距離度量的平動頻率系數能夠反映振動臺輸入頻率變化規律。

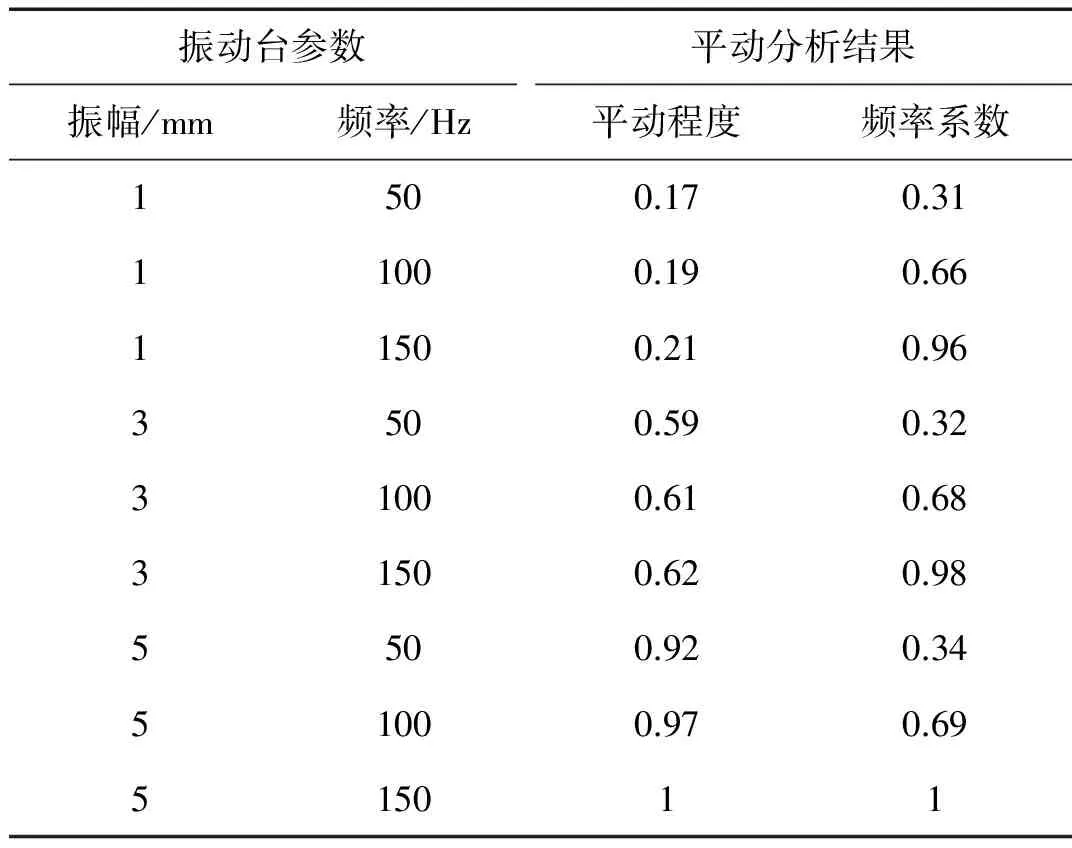
表1 MIMU振動臺試驗結果對比Tab.1 The shaking-table tests results of translationalamplitude and frequency

3.2 轉臺模擬試驗

為驗證輸電線路扭轉分析方法性能，特設計轉臺搖擺運動模擬輸電線路扭轉試驗，將該MIMU系統固定在雙軸轉臺上，如圖6所示，MIMUZ軸垂直臺面，調整臺面水平且使MIMUX軸垂直于臺面轉軸。考慮安裝誤差及MIMU初始數據誤差，轉臺靜止下采集MIMU重力數據作為初始數據段，轉臺以不同角度、頻率搖擺運動下采集MIMU重力數據作為扭轉數據段，Dgmax、DEgmax分別取為轉臺搖擺角/頻率5 deg/15 Hz對應的增廣重力加速度二階中心距、增廣重力加速度相鄰序列段歐式距離，數據分段數l取為30，按照2.2節扭轉分析流程估計MIMU扭轉幅度及頻率。

圖6 MIMU轉臺扭轉試驗Fig.6 Turntable test of MIMU

表2為轉臺做搖擺運動時設定的“搖擺角/頻率”與由上述扭轉分析方法得到的“扭轉度/頻率”估計結果對比。由表2結果知，當轉臺搖擺角分別設為小角1 deg、中角3 deg、大角5 deg時，計算的扭轉程度Dg分別落在(0.18,0.22)、(0.58,0.61)、(0.93,1)區域，扭轉程度與搖擺角近似線性，可見本文基于重力加速度二階中心距度量的扭轉幅度對輸入搖擺角有較好的跟隨性；當轉臺的輸入頻率依次為5 Hz、10 Hz、15 Hz時，計算的頻率系數Fg依次屬于(0.32,0.35)、(0.65,0.68)、(0.97,1)，頻率系數近似正比輸入頻率，可見上述基于歐氏距離度量的扭轉頻率系數較好反映了轉臺輸入頻率變化規律。

表2 MIMU轉臺試驗結果對比Tab.2 The turntable tests results of torsional amplitudeand frequency

3.3 輸電線路模擬試驗

為進一步驗證上述輸電線路振動分析方法性能，按一定比例設計了輸電線路模型，將MIMU系統按1.1節方案安裝于模型，如圖7所示。分別于2016-11-01、2016-11-11、2016-11-21各采集一組輸電線路振動數據，考慮MIMU初始數據誤差，輸電線路靜止時采集MIMU數據作為初始數據段，將采集的數據按2.3節分析流程處理，估計平動、扭轉幅度及頻率。Damax、DEamax、Dgmax、DEgmax取值同前，l取為30。

圖7 輸電線路模型試驗Fig.7 Test of MIMU on transmission lines model

圖8為采集并提取的某組輸電線路平動加速度及估計的平動程度和頻率系數。觀察圖8可知，各軸振動越大，平動程度也隨之變大，說明各軸向平動程度對各軸向振動具有較好跟隨性；各軸振動變化越劇烈，對應平動頻率系數越大，平動頻率系數對各軸平動變化劇烈度具有較好跟隨性。

圖9為采集的同組輸電線路扭轉時X,Z軸重力及估計的扭轉程度和頻率系數。觀察圖9，X軸、Z軸重力數據變化越大越快，說明扭轉幅度頻率也越大，對應扭轉程度和扭轉頻率數值也越大，能夠反映扭轉變化規律。

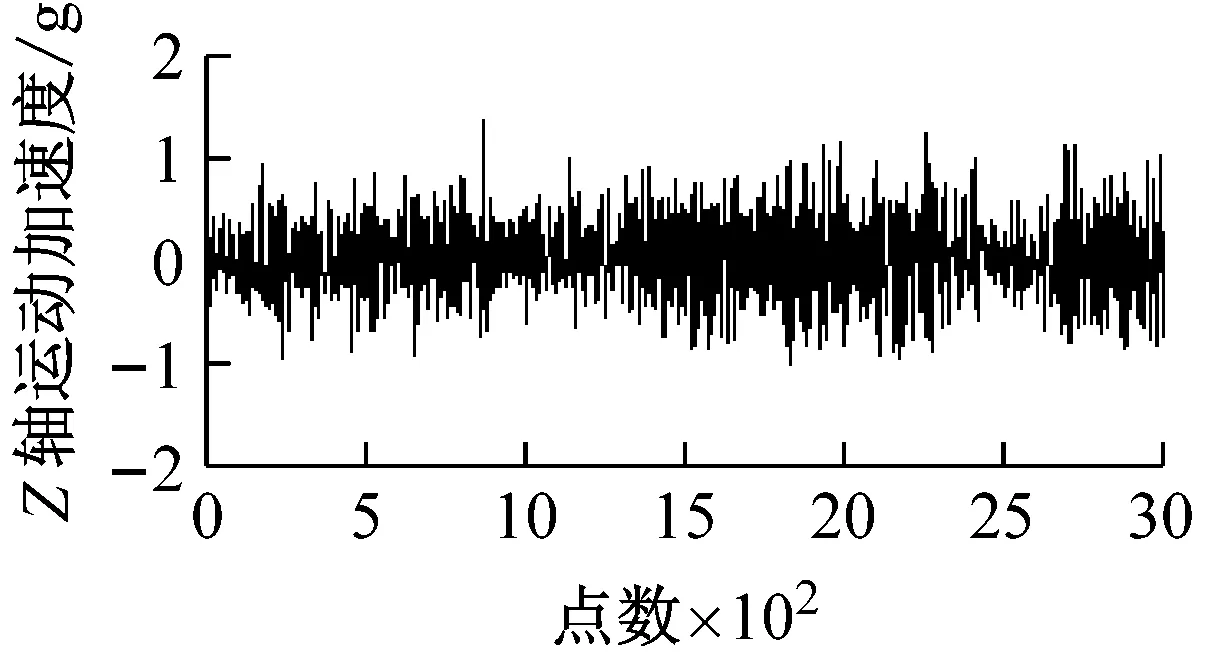
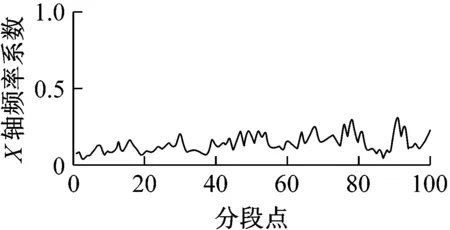
圖8 輸電線路模型平動分析Fig.8 Analysis of transmission line model translational movement

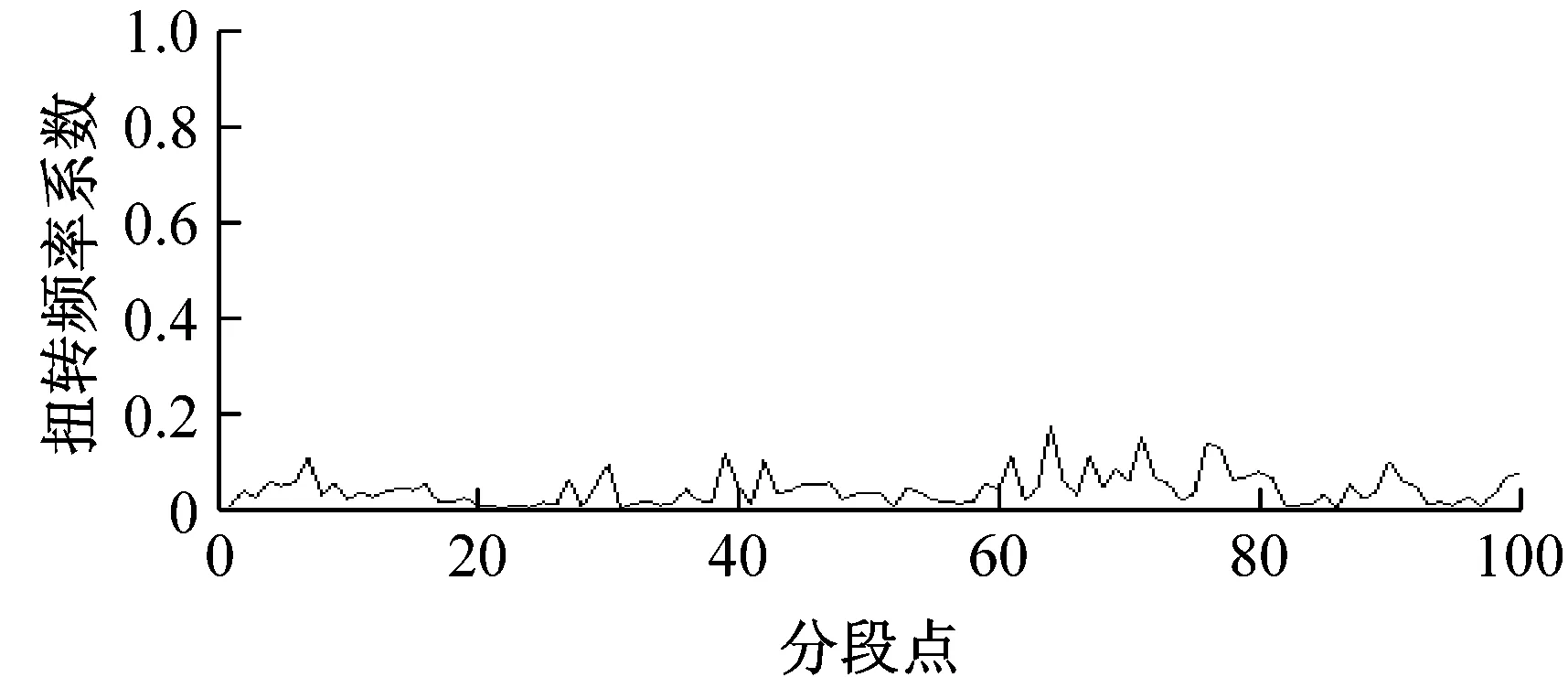
圖9 輸電線路模型扭轉分析圖Fig.9 Analysis of transmission line model torsional movement

圖10為采集并提取的三組輸電線路運動數據根據2.3節輸電線路振動分析流程所繪振動幅度、頻率綜合分布圖，從圖中可發現，Z軸平動點分布于{(x,y),x∈(0,0.4),y∈(0,0.2)}區域，X軸平動點分布于{(x,y),x∈(0,0.3),y∈(0,0.1)}區域，Y軸平動不明顯，說明平動程度和頻率較小；扭轉點集中于{(x,y),x∈(0,0.1),y∈(0,0.02)}區域，說明扭轉程度及頻率很小，綜上可知，該段時間內輸電線路振動程度較小。連續長期監測輸電線路振動并計算振動(扭轉)程度和頻率，根據平動(扭轉)程度與幅度(搖擺角)、頻率系數與頻率正比關系，結合設定的最大幅度(扭轉角度)及頻率可獲知本地區輸電線路振動特點，為后續振動阻尼器設計，提供參數依據。

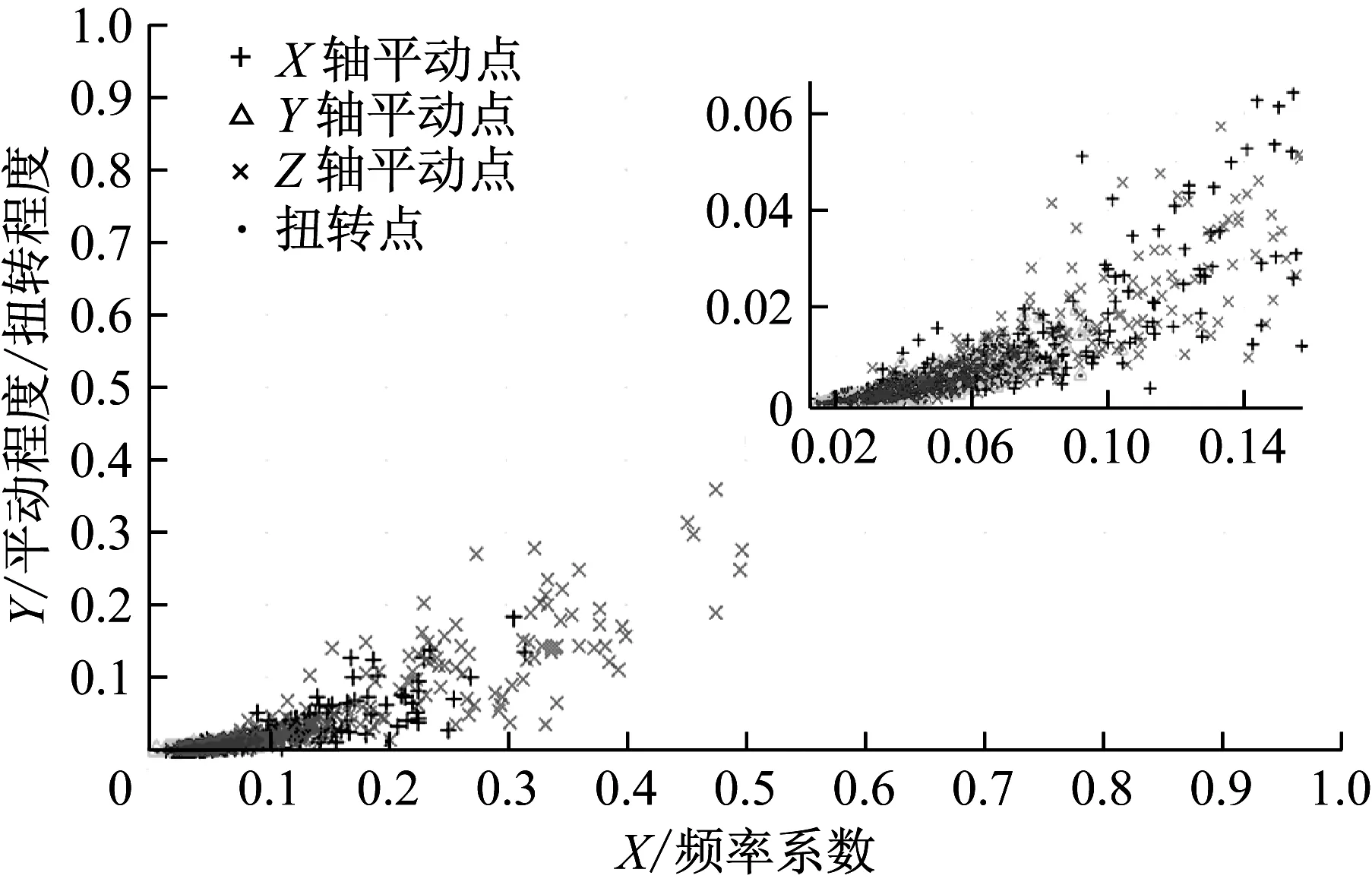
圖10 振動幅度頻率綜合分布圖Fig.10 Comprehensive distribution map about the vibration amplitude-frequency of transmission line

4 結 論

針對通過多點MIMU解算導線運動軌跡來分析本地區輸電線路振動特點精度不高且難以實現長期監測，提出一種慣性測量參數的時間序列分段模式的輸電線路振動分析方法。設計了一種MIMU測量節點并采用一定長度的彈性桿進行信號物理放大和防磁干擾，通過對MIMU時間序列變異度分析和相似性度量，預測輸電線路平動、扭轉程度及頻率，進而評估輸電線路運動異常程度。最后設計了振動臺、轉臺模擬平動、扭轉試驗和輸電線路模型實驗，采集不同平動、扭轉程度及頻率時的MIMU信號，實驗結果表明，處理數據結果能夠反映輸電線路平動和扭轉變化規律，說明輸電線路運動分析方法是有效的，且實施方案易行，計算簡單，無累計誤差，工程實用性較強, 可以為實現長期監測本地區輸電線路振動幅度和頻率提供參考，以進一步為輸電線路振動阻尼控制器設計提供參數。

參 考 文 獻

[1] 葉志雄. 輸電線微風振動及次檔距振蕩控制研究[D].武漢:華中科技大學,2009.

[2] 張帆,熊蘭,劉鈺．基于加速度傳感器的輸電線舞動監測系統[J]．電測與儀表,2009,46(1): 30-33．

ZHANG Fan, XIONG Lan, LIU Yu. Transmission lines galloping monitoring system based on accelerometer sensors[J]. Rlectrical Measurement &lnstrumentatinn, 2009, 46(1): 30-33．

[3] 黃官寶,黃新波,趙雪松,等．輸電線路導線舞動在線監測系統設計[J]. 南方電網技術,2009, 3(4):85-89.

HUANG Guanbao, HUANG Xinbo, ZHAO Xuesong, et al. On-line monitoring system design on transmission line galloping[J]. Southern Power System Technology, 2009, 3(4): 85-89.

[4] 王有元,任歡,杜林. 輸電線路導線舞動軌跡監測分析[J]．高電壓技術,2010,36(5): 1113-1118．

WANG Youyuan, REN Huan, DU Lin.Analysis on conductor galloping track monitoring of transmission line[J]. High Voltage Engineering, 2010,36(5): 1113-1118.

[5] 黃新波,趙隆,周柯宏,等. 采用慣性傳感器的輸電導線舞動監測系統[J]．高電壓技術,2014,40(5): 1312-1319．

HUANG Xinbo, ZHAO Long, ZHOU Kehong, et al. Conductor galloping monitoring system based on inertial sensor for tansmission lines[J]. High Voltage Engineering,2014,40(5): 1312-1319.

[6] 邵穎彪,楊曉輝,郭薇,等. 基于九軸傳感器監測導線舞動的研究方法[J]. 智能電網,2015, 5(1): 1-8.

SHAO Yingbiao, YANG Xiaohui, GUO Wei, et al. Monitoring galloping of transmission lines based on nine-axis sensors[J].Smart Grid, 2015, 5(1): 1-8.

[7] 晏致濤,李正良,楊振華．基于結點6自由度的輸電線舞動有限元分析[J]．振動與沖擊,2011, 30(8): 112-117．

YAN Zhitao, LI Zhengliang, YANG Zhenhua. Finite element modeling of transmission line galloping based on 6-DOFs nodes[J].Journal of Vibration and Shock,2011, 30(8): 112-117．

[8] 黃新波,趙隆,舒佳,等. 輸電線路導線微風振動在線監測技術[J]. 高電壓技術,2012,38(8):1863-1870.

HUANG Xinbo, ZHAO Long, SHU Jia, et al. Online monitoring conductor aeolian vibration of transmission lines[J]. High Voltage Engineering, 2012, 38(8):1863-1870.

[9] 王寶成. 油氣彈簧阻尼器在輸電線路防舞動的應用[J]. 內蒙古電力技術,2011,29(3):73-75.

WANG Baocheng. Application of oil vapor spring-dampers in prevention of power transmission line waving[J]. Inner Mongolia Electric Power,2011,29(3):73-75.

[10] LANGLOIS S, LEGERON F. Prediction of aeolian vibration on transmission-line conductors using a nonlinear time history model—Part II: conductor and damper model[J]. IEEE Transactions on Power Delivery, 2014, 29(3):1168-1175.

[11] SAADABAD N A, MORADI H, VOSSOUGHI G. Semi-active control of forced oscillations in power transmission lines via optimum tuneable vibration absorbers: with review on linear dynamic aspects[J]. International Journal of Mechanical Sciences, 2014, 87(4):163-178.

[12] LEE J K, PARK E J, ROBINOVITCH S N. Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions[J]. IEEE Transactions on Instrumentation and Measurement, 2012,61(8):2262-2273.

[13] ALAM M, ROHAC J. Adaptive data filtering of inertial sensors with variable bandwidth[J]. Sensors, 2015,15(2):3282-3298.

[14] 杜永峰,李萬潤,李慧,等. 基于時間序列分析的結構損傷識別[J]. 振動與沖擊,2012, 31(12):108-111.

DU Yongfeng, LI Wanrun, LI Hui, et al. Structural damage identification based on time series analysis[J]. Journal of Vibration and Shock, 2012, 31(12):108-111.

[15] 刁延松,任紅. 基于AR模型和因子分析的結構損傷預警研究[J]. 振動與沖擊,2014, 33(18):115-119.

DIAO Yansong, REN Hong. Structural damage early warning based on AR model and factor analysis[J]. Journal of Vibration and Shock, 2014,33(18):115-119.

[16] YANG Jinxian, LI Zhipeng. Deformation prediction based on MIMU signal[J]. Journal of Computational Information Systems,2014,11(8): 6741-6751.