高溫環境下纖維增強復合材料等效參數預測

陳素芳， 譚志勇， 姜 東， 董萼良， 費慶國(.東南大學 工程力學系,南京 0096;.北京臨近空間飛行器系統工程研究所,北京 00076;3.南京林業大學 機械電子工程學院,南京 0037;.東南大學 機械工程學院,南京 89)

陶瓷基纖維增強復合材料具有熱防護性能好、比強度/比剛度高等優點，廣泛應用于航空、航天領域，進而面臨極端嚴酷的高溫服役環境。高溫環境下結構動態特性分析至關重要，是復合材料熱結構動響應計算、振動控制和優化設計的前提。

在熱結構動態特性分析方面，楊和振等[1]以復合材料層合板為研究對象，研究了在不同溫度條件下復合材料層合板的動力響應，表明復合材料層合板結構的模態參數受到溫度變化的顯著影響。Spivey[2]對C/SiC熱結構操縱面進行了熱載荷狀態下結構的試驗、仿真振動特性分析。Cheng等[3]以加筋板為研究對象，結合材料的熱物理性能和力學性能進行熱載荷狀態下結構的振動特性分析和非均勻溫度場對熱結構模態參數的影響研究。Wu和Wang等[4]分別利用試驗和仿真的方法研究了板在高溫環境下熱模態參數。通過熱模態分析可深入了解溫度梯度、材料參數對結構固有頻率的影響，為熱結構設計提供參考。

為了提高計算效率，復合材料結構的動態分析往往采用等效建模：在常溫條件下，僅需要考慮材料的等效彈性性能[5-6]，但高溫環境下，材料的彈性模量隨溫度變化，溫度梯度將導致結構內部產生熱應力。因此，熱結構動態分析時，應著重關注復合材料的彈性和熱膨脹性能。熱膨脹系數作為表征材料熱穩定性的重要參數，對高溫工作環境下復合材料的動力學性能影響較大，熱應力和熱模態分析等都依賴于材料的熱膨脹性能。

復合材料的熱膨脹性能可以根據其材料組分性能，纖維含量等參數，進行理論分析[7]。20世紀七八十年代，Schapery等[8-9]基于等效彈性矩陣得出了各向同性、多相材料熱膨脹系數的上下限。劉書田等[10]利用均勻化的方法，研究了含有均勻分布球形空洞的空心鋁材料和單向纖維增強復合材料的熱膨脹行為，建立了組分材料性能、體積分數與熱膨脹系數之間的關系。梁軍等[11]針對定向分布微裂紋的纖維增強復合材料，利用Eshelby理論和Mori-Tanaka方法，預報了復合材料的有效熱膨脹系數。盡管人們一直不斷探索材料熱物理性能預測的理論模型和計算方法，但是由于熱物理性能對材料的組成、晶體結構及制備工藝都很敏感，加之復合材料本身結構復雜，所以試驗測定仍是最為直接有效的方法。Tognana等[12]利用光學熱膨脹儀，測量了不同體積含量的顆粒增強復合材料的熱膨脹系數。Pan等[13]采用分離式霍普金斯壓桿，結合加熱裝置的系統，測試3D編織復合材料23 ℃～210 ℃范圍內材料的熱物理性能。

隨著數值計算被引入復合材料熱膨脹系數等效研究，有限元法逐步成為繼理論分析、試驗測定之后的另一種有效手段。燕瑛等[14]基于細觀力學有限元法預報了復合材料熱膨脹系數，并與理論方法結果進行對比。Karadeniz等[15]基于有限元的方法預報了纖維增強復合材料的橫向、縱向熱膨脹系數。有限元法的有效性依賴于計算模型的準確建立，且模型要盡可能地模擬材料內部的真實結構。為此，聶榮華等[16]依據二維編織復合材料的細觀結構特點，提出一種預測該材料的面內熱膨脹系數的單胞模型，充分考慮到編織結構復合材料中的纖維束彎曲和CVI工藝制備陶瓷基復合材料產生的孔洞對熱膨脹系數的影響。盧子興等[17]在三維全五向編織復合材料細觀結構模型的基礎上，建立了單胞參數化有限元模型，計算編織復合材料的熱膨脹系數。Zhang等[18]建立了三維編織復合材料結構不同空間位置的三種單胞模型，施加邊界條件，計算三種情況下的等效彈性參數。Lu等[19]在研究纖維、基體連接界面對編織復合材料熱物理性能的影響時，提出一種三維有限元模型，將紗線考慮成單向纖維增強復合材料并采用代表性體積單元計算其熱物理性能。

本文以單向纖維增強復合材料為對象，通過細觀力學理論推導，建立一種同時預測復合材料彈性參數和熱膨脹系數的方法。并將等效后的均質材料屬性和等效前各組分材料屬性分別建立相應的等效模型和精細化有限元模型，通過計算結構的熱動態特性分析，驗證結構熱參數等效的可行性。在此基礎上，進一步研究不同纖維排布方式、不同單胞模型對參數等效預測結果的影響。

1 理論基礎

1.1 熱彈性力學理論

熱彈性力學中，假設材料的溫度和變形可分別計算，不考慮耦合關系；材料始終處于彈性范圍內，不考慮因溫度產生的非彈性變化；材料變形很小不考慮他們的二階微分項。因此，胡克定律在均勻常值溫度下的本構方程

σij=cijklεkl

(1)

如果考慮溫度變化的影響，而不考慮溫度和變形之間的耦合關系，則材料的本構方程為

σij=cijklεkl+βij(T-T0)=cijklεkl+βijΔT

(2)

式中：βij是在應變為零時測量的熱模量，是一個對稱張量；T0為參考溫度，即彈性模量cijkl測定時的溫度，cijkl也稱為剛度系數。

由式(2)求應變，可得

εij=sijklσkl+αijΔT

(3)

式中：αij為各向異性材料的熱膨脹系數；sijkl為柔度系數。將式(2)展開為矩陣形式則為

(4)

上式21個彈性系數Cij和6個熱系數βij，表示各向異性體全不對稱材料。按照簡化張量標記，見表1。

表1 簡化張量標記Tab.1 Simplified marker of tensor

這樣，式(2)、式(3)簡化為

σi=cijεj+βi(T-T0)=cijεj+βiΔT

(5)

εi=sijσj+αiΔT

(6)

由上述應力應變式(5)、(6)運算，可得剛度系數、柔度系數、熱模量和熱膨脹系數之間的關系

cijskl=δik

(7)

βi=-cijαj

(8)

αi=-sijβj

(9)

式中:δ為克羅尼克符號；β為熱模量；α為熱膨脹系數；c,s分別表示剛度矩陣和柔度矩陣。因此，按照方程式(9)的關系，開展有限元法等效預測過程。

1.2 參數預報步驟

步驟1等效剛度預測

在基準溫度T=T0下，溫差ΔT=0。本構關系式滿足：σ=cijεj，即

(10)

當ε1=1；ε2=ε3=γ4=γ5=γ6=0時，應力矩陣等于剛度矩陣的第一列[c11c21c31c41c51c61]T；依次每施加一個單位正(切)應變所得的應力列陣等于剛度矩陣中相應的一列。

表2和表3分別給出了等效分析的六種工況及六種工況下相應的應變條件。從表3可以看出，單位正(切)應變轉化為相應的位移邊界條件，可以實現單位應變載荷的施加。如工況一，加載x方向單位正應變(εx=1)，轉化為位移邊界條件只需在x=0的面上施加固定約束，x=a的面上施加特定位移a，其余四個面x方向自由，y,z方向約束。

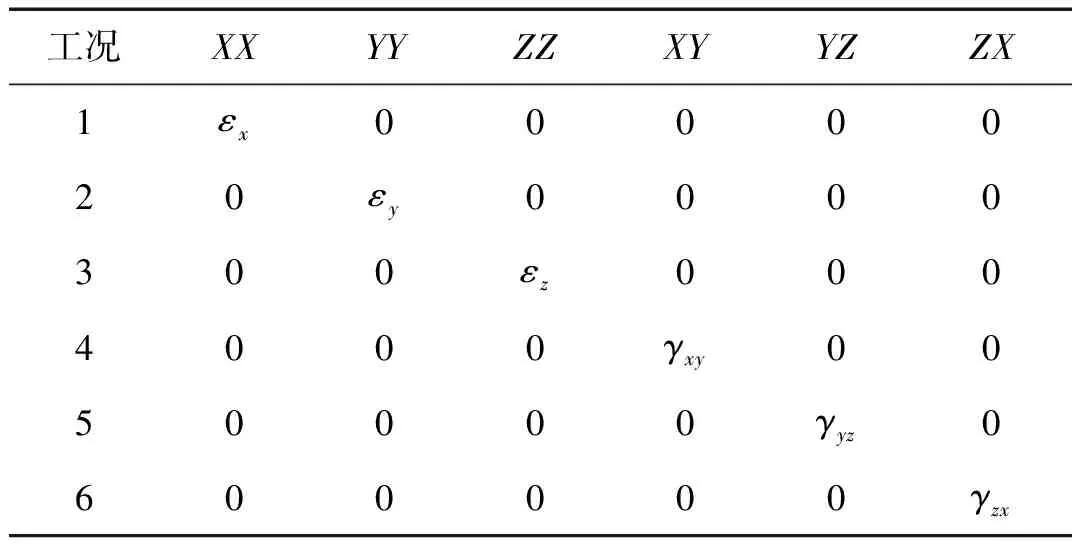
表2 等效分析的六種工況Tab.2 Six cases for equivalent analysis

表3 邊界條件Tab.3 Boundary conditions

由兩種材料構成的細觀不均勻結構，宏觀上將其等效為均質等效體。等效體的應力等于細觀結構的平均應力；等效體的應變等于細觀結構的平均應變

(11)

(12)

不考慮溫度變化時，則平均應力與平均應變之間滿足本構關系

(13)

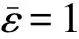
(14)

(15)

對于正交各向異性材料而言，其剛度系數矩陣D滿足

(16)

對應的柔度系數矩陣S

(17)

因此，等效彈性參數及等效主泊松比(v12、v23)和副泊松比(v31)為

(18)

步驟2等效熱模量預測

在T0+ΔT溫度下(ΔT≠0)，使單胞整體結構不發生任何變形(即ε=0)，則式(2)滿足：σ=Dα·ΔT=β·ΔT，即

(19)

采用周期性位移邊界條件，施加單位溫度差值，經穩態熱分析得非均勻溫度場。并將此非均勻場作為結構分析的熱載荷條件進行靜力分析計算單胞的熱應力場。因此，每一個單位溫度差值下，計算得到的應力列矩陣等于熱模量β。

表4、表5分別給出了熱傳導分析時加載的三種工況和對應的邊界條件。求解的熱膨脹系數是在T=T0時的值，如果材料組分(纖維、基體)的性能在溫度變化區間[T0，T1]內不是常量，可將原區間細分為若干子區間，認為每個子區間內材料的性能參數為常數。考慮上述因素，因此在施加邊界條件時，選取的溫差值a、b、c在整個溫差ΔT范圍內，材料參數都保持不變，可以不必細分溫度區間。

編程獲取各個單元應力、單元體積，按式(20)體積平均，求解平均熱應力

(20)

表4 熱傳導分析的三種工況Tab.4 Three cases for heat transfer analysis

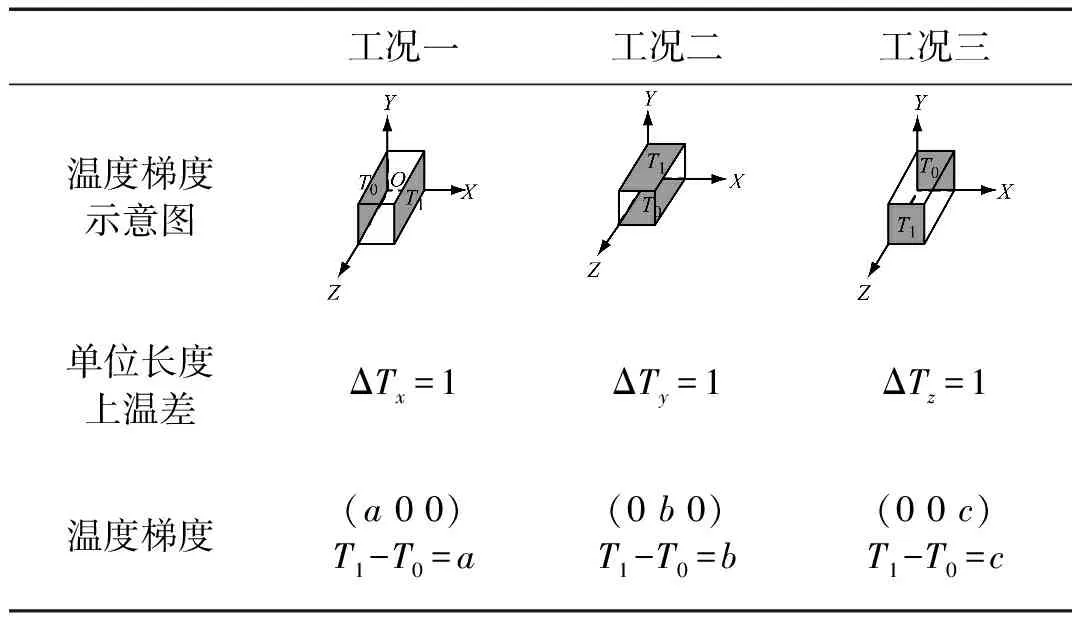
表5 給定的邊界條件Tab.5 The given boundary conditions

由步驟1可知，單位應變場的加載不易實現，轉化為位移場加載。同理，單位長度的溫差在未經熱分析之前更不易確定和加載。因而，首先對結構兩對面施加任意的溫度差值，經穩態熱分析，可求得單元的溫度梯度，然后將平均熱應力歸一化，即得單位溫度梯度下結構的熱應力，即等效熱模量。

(21)

式中：βe表示等效熱模量；Δ表示單位長度的溫度梯度的平均值。

步驟3等效熱膨脹系數

由第1步得到的等效剛度矩陣，求逆，得等效柔度矩陣；由第2步求得等效熱模量，按式(9)求得到等效熱膨脹系數。其中，等效模型的密度根據纖維、基體各自的體積分數求解計算。

圖1給出了單向纖維增強復合材料熱膨脹系數預測流程圖。首先對單胞模型進行剛度預測，得到復合材料的等效剛度矩陣，然后對該單胞模型進行熱傳導分析，獲得非均勻分布溫度場，將其作為溫度載荷，加載于結構進行結構分析，獲得結構的平均熱應力，由式(21)進而得等效熱模量。最后，由式(9)求得結構的等效熱膨脹系數。

圖1 熱膨脹系數等效預測流程圖Fig.1 Prediction flow chart for equivalent thermal expansion coefficient

2 單胞模型

通過對組成材料的性能的了解，再由給定纖維增強結構的幾何參數，應用解析的方法來預報復合材料的宏觀力學性能，就是細觀力學的研究方法。細觀力學理論假設了纖維理想黏結，均勻分布在整個基體中，且材料中的孔隙和氣泡很小。復合材料的紗線是由許多纖維與基體合成的單向纖維增強復合材料柱。按照纖維在基體中排布方式的不同，取正方形排列、六邊形排列，如圖2(a)、(b)所示，圖2(c)正方形排列纖維束對應的代表性體積單元，圖2(d)六邊排列纖維束對應的代表性體積單元,只要對圖2(c)、(d)進行平移變換、鏡面對稱就能形成整個宏觀結構材料。

(a)纖維束正方形排列(b)纖維束六邊形排列(c)正方形排列對應的胞元(d)六邊形排列對應的胞元

圖2 纖維排列分布及選取的單胞

Fig.2 Fiber distribution and selection of the unit cell

圖3給出了單胞有限元模型。單胞II和IV分別為單胞Ⅰ和Ⅲ代表性體積單元(RVE)。縮減的RVE細觀結構模型，一般會極大增加周期性邊界條件的施加難度。但由于等效預測給定邊界條件在單胞和代表性體積單元上的作用面有所不同，因此，取單胞I、III作為研究對象的同時，代表性體積單元(單胞II、IV)也作為研究對象。網格劃分時保證網格在空間上滿足周期性的要求。設單胞中基體為各項同性，纖維為橫觀各向同性材料。纖維、基體的彈性性能、熱物理性能的材料參數如表6、表7所示。

(a)單胞I(b)單胞Ⅱ(c)單胞Ⅲ(d)單胞Ⅳ

圖3 不同單胞的有限元模型

Fig.3 Different finite element model of unit cell

圖4分別給出了四種單胞施加6種基于單位應變載荷(εx，εy，εz，γxy，γyz，γzx)的邊界條件得到的應力分布云圖。由圖4(a)、(b)可以看出，由于單胞Ⅱ是單胞Ⅰ的1/4代表性體積單元，在施加周期性位移邊界條件后靜力分析過程中，兩者的應力云圖分布基本一致：基體的應力明顯高于紗線所受應力，由于基體的彈性性能高于紗線，按照纖維、基體剛度大小分配原則，導致纖維所受應力小于基體應力。同時，從工況一對比來看，單胞Ⅰ、Ⅱ的應力細微有所區別，這主要由于單胞Ⅱ受邊界約束的六個表面相比于單胞Ⅰ的六個邊界約束面同時分布有纖維和基體，進而使兩種材料所受應力重新分配。

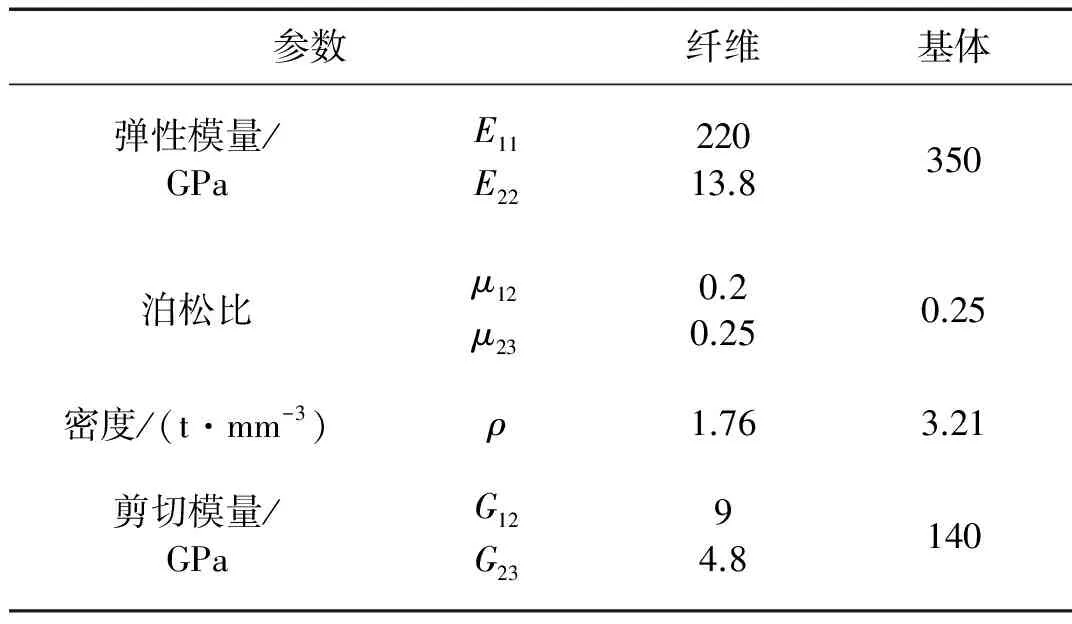
表6 纖維和基體的彈性性能(C纖維/SiC基體)Tab.6 Elastic properties for the fiber and matrix

表7 纖維和基體的熱物理性能Tab.7 Thermophysical properties for the fiber and matrix

(a) 單胞I應力云圖

(b) 單胞II應力云圖

(c) 單胞III應力云圖

(d) 單胞IV應力云圖圖4 不同單胞在六種單位應變工況下的應力云圖Fig.4 Stress distribution of unit cells in six units strain conditions

按式(11)～(16)，計算得等效剛度矩陣。表8、表 9分別給出了四種單胞的等效剛度矩陣。其中，“/”前為單胞I、III的等效剛度矩陣，“/”后為代表性體積單元(單胞II、IV)的等效剛度矩陣。對比表8、表 9的計算結果可以看出，同一類型纖維排列方式下，兩種單胞取法的計算結果非常接近。僅在C44、C55、C66中存在微小差異。由等效剛度矩陣求逆，按式(18)可求得等效彈性參數。

表8纖維束正方形排列對應單胞Ⅰ/Ⅱ的等效剛度矩陣

Tab.8EquivalentstiffnessmatrixofunitcellI/IIunderfiberbundlesquarearrangement

GPa

表9纖維束六邊形排列對應單胞III/IV的等效剛度矩陣

Tab.9EquivalentstiffnessmatrixofunitcellI/IIunderfiberbundlehexagonalarray

GPa

由工程彈性常數互等關系，可求得副泊松比。從表10中可以看出，兩種排列方式對應的單胞等效后都表現橫觀各向同性，但由于纖維束六邊形排列的不對稱性，導致其等效結果稍稍偏離橫觀各向同性的特點；纖維排列方式對橫向彈性模量影響較大，正方形排列的橫向彈性模量大于六邊形的橫向彈性模量；而軸向彈性模量和纖維排列方式無關；同一種纖維排布方式的單胞，其單胞尺寸的大小對剪切模量影響很大。這主要由代表性體積單元(單胞Ⅱ、Ⅳ)被施加周期性邊界條件的作用面和單胞(I、III)有所不同造成的。

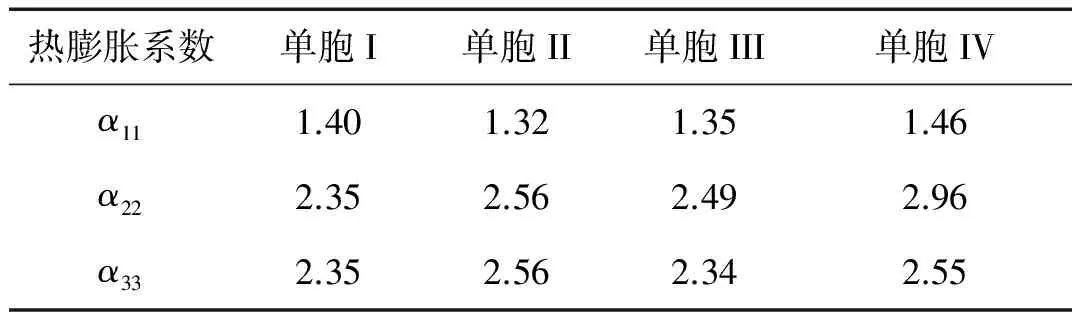
由平均熱應力計算得等效熱模量，按式(20)、(21)及式(9)求得細觀結構等效熱膨脹系數,如表11所示。

3 結果比較

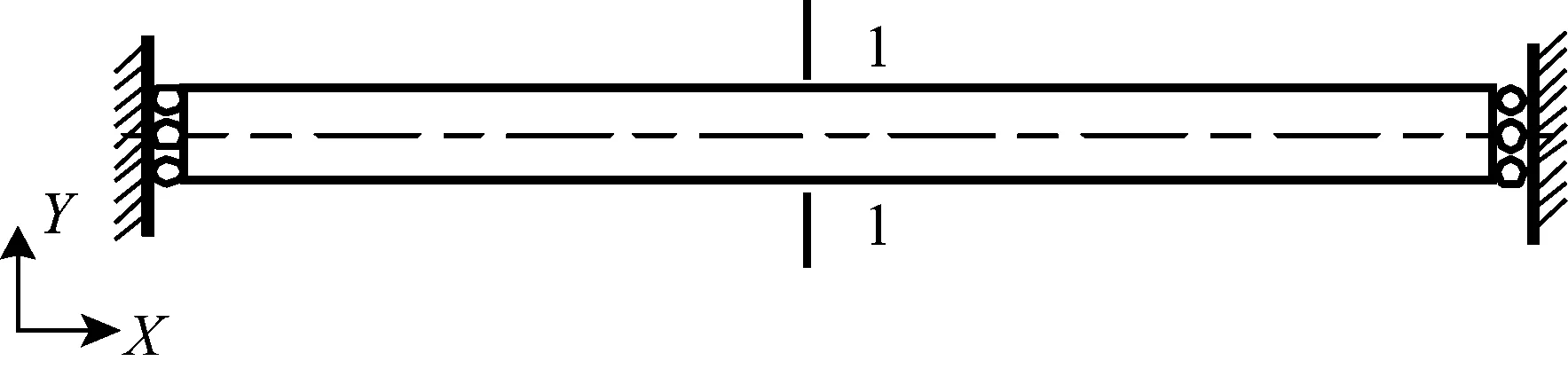
為驗證等效參數的準確性、合理性，將纖維增強復合材料進行精細化有限元建模和等效建模。計算結構非線性熱模態，邊界條件兩邊簡支，整體結構施加100 ℃均勻溫度場，對比精細化模型和等效模型的熱模態頻率及振型。如圖5所示，首先建立復合材料的梁模型(尺寸:800 mm×10 mm×10 mm)，通過對比梁的精細化有限元模型(正方形排布精細化模型180萬個單元，六邊形排布精細化模型208萬個單元)和均質等效模型(8萬個單元)，驗證x方向等效的準確性。然后，建立復合材料板(尺寸:2.5 mm×100 mm×200 mm)，通過對比板的精細化有限元模型(正方形排布精細化模型11.25萬個單元，六邊形排布精細化模型為130萬個單元)與其均質等效模型(6萬個單元)，驗證y,z方向參數等效預測的準確性。梁、板結構精細模型，在隨著單元網格數目逐漸加密的同時，有限元的解基本保持不變，且單元網格數目已達兩百萬個單元，解的收斂性保持較好；等效模型網格數目雖大大下降，但由于等效模型材料屬性已預測為均質的橫觀各向同性材料，目前的單元個數已經可以滿足精度要求。而且，從等效前、后動態特性對比結果可以看出，兩者有限元解的誤差很小，滿足精度要求。

表10不同單胞對應的等效彈性參數

Tab.10EquivalentelasticparametersofunitcellsGPa

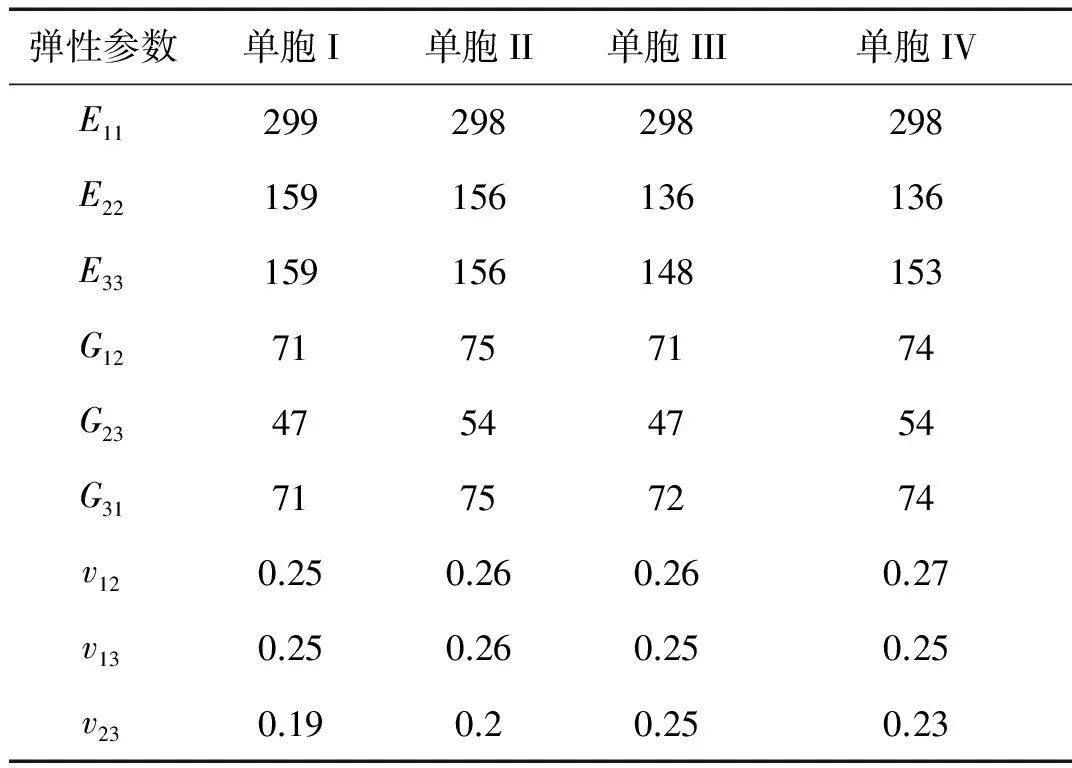
表11不同單胞的等效熱膨脹系數(×10-6)

Tab.11Theequivalentcoefficientofthermalexpansionofunitcells(×10-6) GPa

梁

板圖5 梁、板幾何模型Fig.5 Geometry model of beam and plate8

圖6和圖7分別給出了梁、板等效前、后精細有限元模型和等效模型。(a)為正方形排列纖維束精細化梁模型，(b)是六邊形排布的精細化梁模型，纖維體積分數均為40%。圖(c)為單胞等效后的均質等效模型，材料參數值如表10和表11所示。

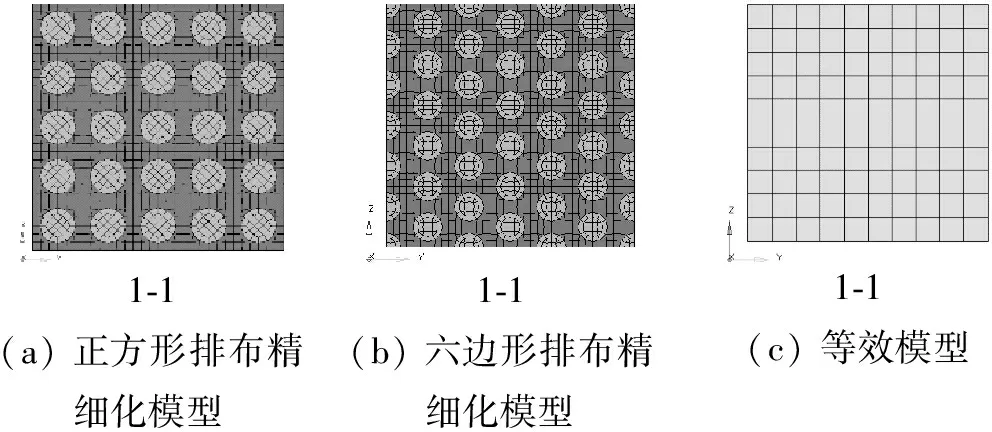
1?1(a)正方形排布精細化模型1?1(b)六邊形排布精細化模型1?1(c)等效模型

圖6 梁等效前、后有限元模型

Fig.6 Finite element model of beam between equivalent before and after

2?2(a)正方形排布精細化模型2?2(b)六邊形排布精細化模型2?2(c)等效模型

圖7 板等效前、后有限元模型

Fig.7 Finite element model of plate between equivalent before and after

表12和表13給出了梁模型等效前、后結構的熱模態頻率和對應的誤差。其中，正方形排布纖維束精細模型的熱模態頻率與均質等效模型的熱模態頻率最大誤差為0.4%；六邊形排布纖維束最大誤差0.7%，均在合理范圍內。可見，由本文提出的預測復合材料熱膨脹系數的方法是合理有效的，從而驗證了本文預測復合材料熱膨脹系數及工程彈性參數方法的正確性。

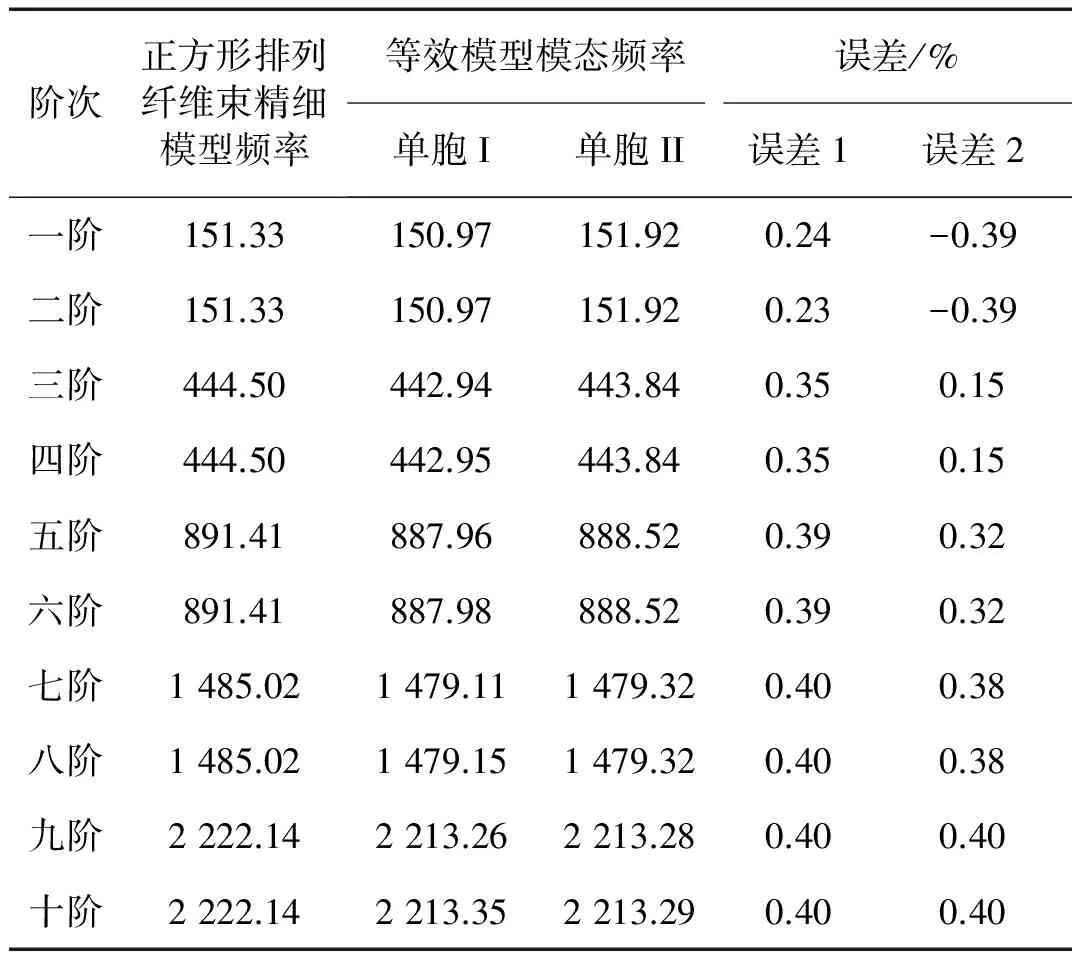
表12 梁等效前后熱模態頻率對比Tab.12 Comparison of beam thermal modal frequencybetween equivalent before and after

表13 梁等效前后模態頻率對比Tab.13 Comparison of beam thermal modal frequencybetween equivalent before and after

表14和表15給出了復合材料板在等效前、后結構的熱模態及其對應誤差。由表中結果可以看出，相比于梁等效前后對比結果，板在等效前、后存在一定的誤差。說明在整個等效預測過程中，x方向預測精度較高；y,z方向的預測雖有一定誤差，但也在合理范圍之內。

由上述四個表對比分析可知，不同類型單胞之間，單胞I、II比單胞III、IV預測準確，說明纖維排布方式對參數等效預測存在影響；同一纖維排布方式下，代表性體積單元越大，預測數據誤差更小，即單胞I比單胞II預測結果合理，單胞III比單胞IV 預測結果精準。這主要是由于縮減的代表性體積單元極大增加了周期性邊界條件的施加難度。除非在極其復雜的非線性問題中，否則，代表性體積單元并不作為等效預測分析的首選。

表14 板等效前后模態頻率對比Tab.14 Comparison of plate thermal modal frequencybetween equivalent before and after

表15 板等效前后模態頻率對比Tab.15 Comparison of plate thermal modal frequencybetween equivalent before and after

4 結 論

(1)依據細觀力學基礎，推導了復合材料熱膨脹系數的公式，建立一種簡潔的等效熱、力學性能的有限元預測方法。針對預測結果，分別進行精細化建模和等效建模，對比等效前、后結構的熱模態及振型，驗證了本文方法的可行性及有效性。

(2)本文所提出的等效熱膨脹系數公式和有限元預測分析方法，不但預測結構的熱膨脹系數，而且可以一并預測復合材料彈性參數。

(3)不同纖維排布方式下，正方形排布纖維束預測結果比六邊形排布纖維束預測精度高；同一纖維排布方式下，單胞的預測結果較縮減后的RVE預測結果精度高。

(4)該預測熱膨脹系數的方法，可以預測復合材料結構在室溫下熱膨脹系數的值，還可以預測不同高溫下的復合材料的熱膨脹系數。為其他新型構型的復合材料彈性、熱膨脹性能的預報提供參考。

參 考 文 獻

[1] 楊和振, 李華軍. 溫度變化下復合材料層合板的試驗模態分析[J]. 復合材料學報, 2008, 25(2): 149-155.

YANG Hezhen, LI Huajun. Experimental modal analysis of the composite laminates with temperature variation[J].Acta Materiae Compositae Sinica, 2008, 25(2): 149-155.

[2] SPIVEY N D. High-temperature modal survey of a hot-structure control surface[C]∥ICAS 27th International Congress of the Aeronautical Sciences. Nice, France: ICAS, 2010.

[3] CHENG H, LI H, ZHANG W, et al. Effects of radiation heating on modal characteristics of panel structures[J]. Journal of Spacecraft and Rockets, 2015, 52(4): 1228-1235.

[4] WU D, WANG Y, SHANG L, et al. Experimental and computational investigations of thermal modal parameters for a plate-structure under 1 200 °C high temperature environment[J]. Measurement, 2016, 94: 80-91.

[5] JIANG Dong, ZHANG Dahai, FEI Qingguo, et al. An approach on identification of equivalent properties of honeycomb core using experimental modal data[J]. Finite Elements in Analysis and Design, 2014, 90: 84-92.

[6] JIANG Dong, LI Yanbin, FEI Qingguo, et al. Prediction of uncertain elastic parameters of braided composites[J]. Composite Structures, 2015, 126, 123-131.

[7] 黃爭鳴. 復合材料細觀力學引論[M].北京:科學出版社, 2004: 69-73.

[8] SCHAPERY R A. Thermal expansion coefficients of composite materials based on energy principles[J]. Journal of Composite Materials, 1968, 2(3): 380-404.

[9] ROSEN B W, HASHIN Z. Effective thermal expansion coefficients and specific heats of composite materials[J]. International Journal of Engineering Science, 1970, 8(2): 157-173.

[10] 劉書田, 程耿東. 基于均勻化理論的復合材料熱膨脹系數預測方法[J]. 大連理工大學學報, 1995, 35(4): 451-457.

LIU Shutian, CHENG Gengdong. Homogenization-based method for predicting thermal expansion coefficients of composite materials[J]. Journal of Dalian University of Technology, 1995, 35(4): 451-457.

[11] 梁軍, 陳曉峰. 含缺陷纖維增強復合材料熱膨脹系數預報[J]. 哈爾濱工業大學學報, 1997, 29(3): 36-38.

LIANG Jun, CHEN Xiaofeng. Thermal expansion coefficients of fiber composite materials containing matrix microcracks[J] Journal of Harbin Institute of Technology University, 1997, 29(3): 36-38.

[12] TOGNANA S, SALGUEIRO W, SOMOZA A, et al. Influence of the filler content on the thermal expansion behavior of an epoxy matrix particulate composite[J]. Materials Science and Engineering: B, 2009, 157(1): 26-31.

[13] PAN Z, GU B, SUN B. Longitudinal compressive behavior of 3D braided composite under various temperatures and strain rates[J]. Applied Physics A, 2014, 118(4): 1315-1337.

[14] 燕瑛，李劍峰. 復合材料熱膨脹性能的細觀分析模型與預報[J]. 北京航空航天大學學報, 2013, 39(8): 1069-1085.

YAN Ying, LI Jianfeng. Prediction of thermal expansion properties for composites by micromechanical analysis model[J] Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(8): 1069-1085.

[15] KARADENIZ Z H，KUMLUTAS D. A numerical study on the coefficients of thermal expansion of fiber reinforced composite materials[J]. Composite Structures, 2007, 78(1): 1-10.

[16] 聶榮華, 矯桂瓊, 王波. 二維編織C/Sic復合材料的熱膨脹系數預測[J]. 復合材料學報, 2008, 25(2): 109-114.

NIE Ronghua, JIAO Guiqiong, WANG Bo. Prediction on coefficient of thermal conductivity for 2D braided C/SiC composites[J].Acta Materiae Compositae Sinica, 2008, 25(2): 109-114.

[17] 盧子興, 王成禹, 夏彪. 三維全五向編織復合材料彈性性能及熱物理性能的有限元分析[J].復合材料學報, 2013(3): 160-167.

LU Zixing, WANG Chengyu, XIA Biao. Finite element analysis of elastic property and thermo-physical properties of three-dimensional and full five-directional braided composites[J]. Acta Materiae Compositae Sinica, 2013(3): 160-167.

[18] ZHANG C, XU X. Finite element analysis of 3D braided composites based on three unit-cells models[J]. Composite Structures, 2013, 98: 130-142.

[19] LU Z, WANG C, XIA B, et al. Effect of interfacial properties on the thermophysical properties of 3D braided composites: 3D multiscale finite element study[J]. Polymer Composites, 2014, 35(9): 1690-1700.