自適應混沌量子粒子群算法及其在WSN覆蓋優化中的應用
周海鵬,高 芹,蔣豐千,余大為,喬 焰,李 旸
(1.安徽農業大學 信息與計算機學院, 合肥 230036; 2.農業部農業物聯網技術集成與應用重點實驗室(安徽農業大學),合肥 230036)(*通信作者電子郵箱ly-and@qq.com)
0 引言
覆蓋控制一直是無線傳感器網絡(Wireless Sensor Network, WSN)的研究熱點,它反映了WSN提供感知服務的質量。保證對監測區域一定的覆蓋是WSN發揮功能的關鍵。在實際應用場景中,受目標區域物理環境的限制,傳感器節點一般采用撒播方式隨機部署。然而,該方式部署的WSN存在節點分布不均、覆蓋率低、冗余度高等缺陷。部署動態節點,通過覆蓋優化算法對初始部署的節點位置進行調整,可以取得較好效果。
群體智能算法給解決WSN覆蓋優化問題帶來了新思路,近年來大量國內外學者將群體智能算法應用于WSN覆蓋控制中[1-2]。文獻[3]將遺傳算法應用到WSN的覆蓋控制中,取得了優化,但是算法較復雜,收斂速度較慢。文獻[4]中提出了一種基于外推人工蜂群算法的WSN部署優化方法,雖然收斂較快,但是與其他算法相比,在覆蓋率的提升上沒有明顯優勢。粒子群算法由于具有控制參數少、收斂速度快、易于實現等特點,被廣泛應用于WSN覆蓋優化中[5-6]。文獻[7]中提出了一種基于改進的粒子群算法,引入了種子雜交策略,取得較好效果,比遺傳算法更容易實現。文獻[8]中提出了一種基于混沌粒子群的WSN覆蓋優化算法,比標準粒子群有更好的全局搜索能力,不過到搜索后期粒子以大概率進行混沌擾動不利于精細化搜索,計算復雜度有較大幅度增加。文獻[9]將進化因子和聚合因子引入粒子群優化(Particle Swarm Optimization, PSO)算法中的慣性權重系數中,并采取碰撞回彈策略保證粒子群的多樣性,對WSN覆蓋優化效果較明顯。文獻[10]將混沌量子粒子群算法應用于WSN覆蓋優化中,提出了精英個體適應值方差早熟判斷機制,提高了WSN的覆蓋率,但是該早熟判斷機制存在局限性,不能完全反映粒子的聚集情況。
為了提高WSN的覆蓋性能,針對傳統粒子群算法的不足,本文從種群多樣性的角度出發,將種群分布熵和平均粒距兩個多樣性評價指標引入量子粒子群算法的優化過程中,提出了一種基于動態自適應混沌量子粒子群(Dynamic Self-Adaptive Chaotic Quantum-behaved PSO, DACQPSO)的WSN覆蓋優化算法。最后通過仿真實驗驗證了算法的性能。
1 WSN覆蓋優化數學模型
1.1 節點感知模型
本文選取了文獻[7]中的概率感知模型來計算WSN的覆蓋率。WSN中傳感器節點si對目標點g的感知概率為:
(1)
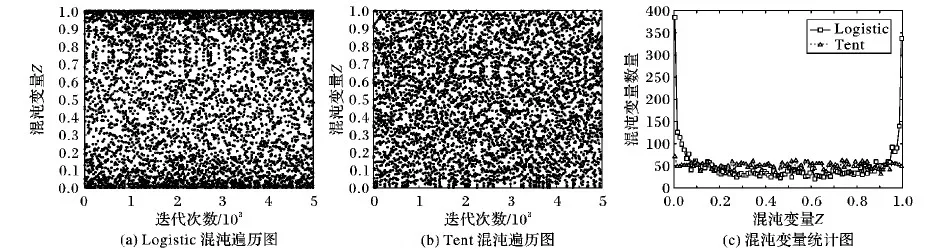
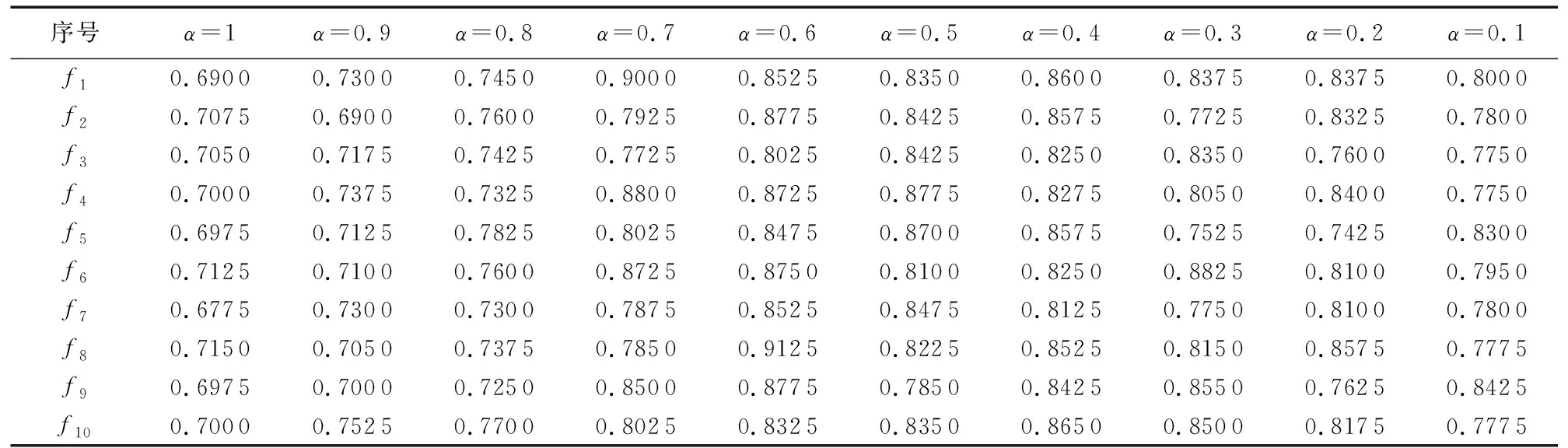
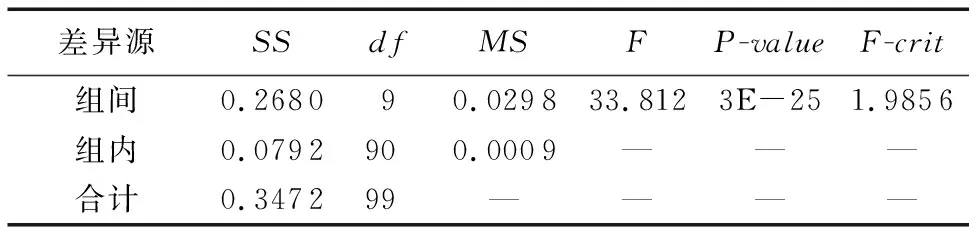
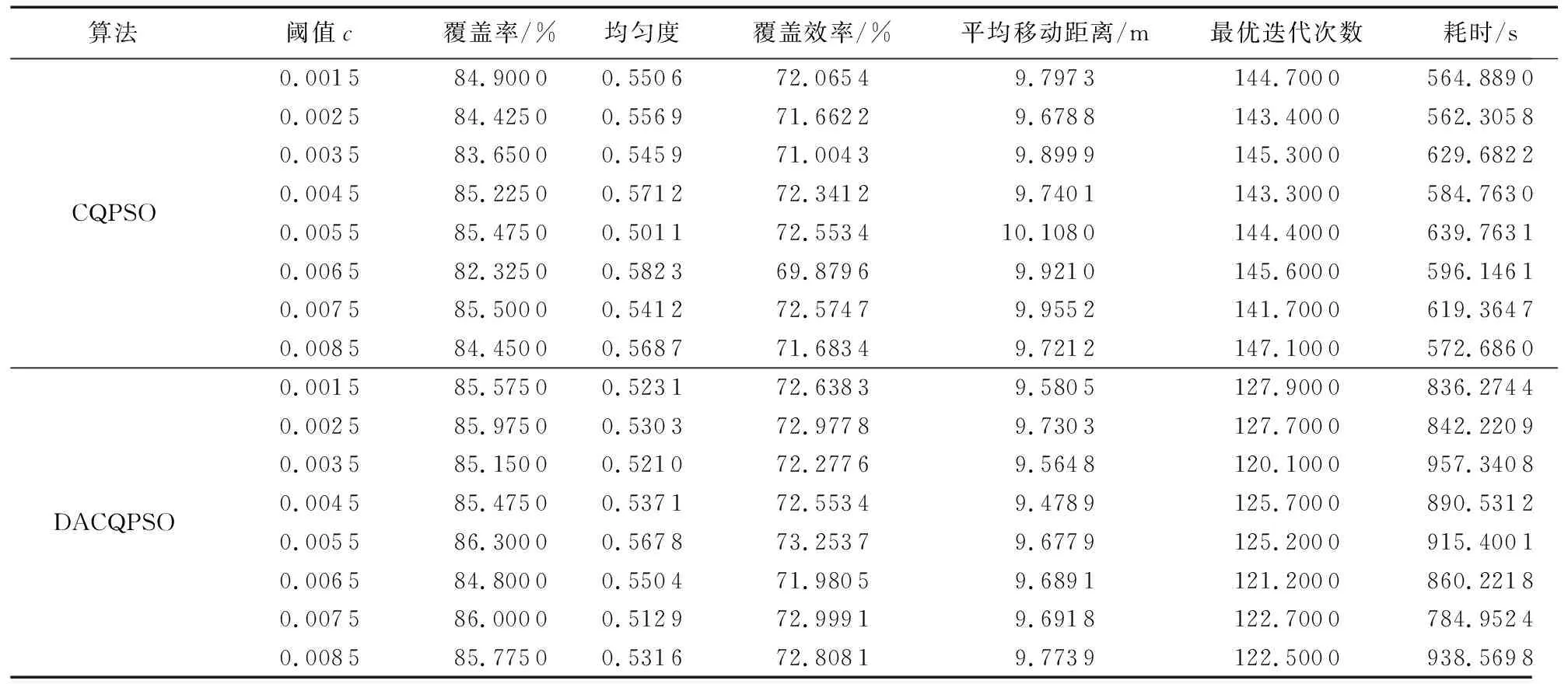
其中:d(si,g)為傳感器節點si與目標點g之間的歐幾里得距離;re(0 為了考察各種WSN部署的優劣性,選取6種常見的指標對覆蓋控制算法作出科學的評估,以便對覆蓋算法作對比分析。 1)覆蓋率。 為了便于計算,將面積為m×n的矩形區域A均勻劃分為m×n個單位面積的網格,并將其簡化成像素點。監測區域內的所有傳感器節點對目標點g的聯合檢測概率為: (2) 其中:sall表示WSN中所有檢測目標點g的傳感器節點的集合。點g能被有效檢測到的條件為: Pr(sall,g)≥Prth (3) 其中:Prth為檢測概率閾值。節點集S對監測區域的覆蓋率Rarea(S)為節點集的覆蓋面積與監測區域的總面積的比值[11],即滿足式(3)的單元網格數量和與監測區域總的單元網格數量之比。 (4) 2)均勻度。 均勻度反映節點分布的均勻程度,計算公式如下: (5) 其中:n為節點總數;ki為節點i的鄰居節點數;Di, j為節點i和節點j之間的歐幾里得距離;Mi為節點i與其所有鄰居節點之間距離的平均值。覆蓋均勻度越小網絡覆蓋質量越好。 另外還選取覆蓋效率[12-13]、平均移動距離、最優迭代次數和算法耗時4個指標,限于篇幅不作具體介紹。 粒子群優化(PSO)算法[14]擁有進化計算和群體智能等特點,但它不能保證收斂到全局最優甚至局部最優[15],盡管對PSO算法作了眾多改進[16-20],實際上改進的效果有限。 國內江南大學的孫俊等[21-22]根據量子力學理論,建立δ勢阱勢能場模型,于2004年提出了量子行為粒子群優化(Quantum-Behaved PSO, QPSO)算法,之后量子粒子群優化算法得到了廣泛的研究與應用。 PSO算法在進化過程中始終維持兩個最優位置:1)粒子i(i=1,2,…,M,M為種群規模)的個體最好位置pbesti(t),表示為Pi(t)=[Pi,1(t),Pi,2(t),…,Pi,N(t)]T(N為問題維度)。2)種群全局最好位置gbest(t),表示為Pg(t)=[Pg,1(t),Pg,2(t),…,Pg,N(t)]T。若優化模型為maxf(x),f(x)為適應度函數。其更新公式為: (6) (7) Clerc[16]分析PSO算法的收斂性時發現,粒子i以pbest和gbest之間的隨機點Qi(t)=[Qi,1(t),Qi,2(t),…,Qi,N(t)]T為吸引子,其坐標為: Qi, j(t)=φi, j(t)·Pi, j(t)+[1-φi, j(t)]·Pg, j(t) (8) 其中:φi, j(t)~U(0,1),1≤j≤N。 量子粒子群算法以點Qi(t)為吸引勢,建立δ勢阱場來構筑粒子的量子束縛態,使得群體具有聚集態。通過解粒子在δ勢阱中運動的定態Schr?dinger方程得到波函數,再通過逆變換法得到粒子位置的更新方程[23]為: Xi, j(t+1)= (9) 其中:引入了平均最好位置mbest(t)記為C(t),是所有粒子各個最好位置gbest(t)的平均值,即 (10) 其中:α稱為收縮擴張系數(Contraction-Expansion coefficient, CE coefficient)。QPSO算法可以收斂到全局最優解[24],是全局收斂的隨機搜索算法。 混沌系統具有隨機性、遍歷性和初值敏感性的特性,可以將其應用到隨機搜索中。 混沌映射方程很多,文獻[9,25-26]用的是經典的Logistic混沌方程,其迭代公式為: Zn+1=μZn(1-Zn);n=1,2,…;μ∈(0,4] (11) Tent混沌映射的混沌方程為: (12) 對單個Z0(Z0不取混沌方程的平衡點),μ取4,用Tent映射和Logistic映射分別迭代5 000次,得到兩種混沌映射的遍歷性分析如圖1所示。從圖1可看出:Logistic混沌映射產生的變量軌道點分布不均,落在區間[0,0.1]和[0.9,1]上的變量數量遠遠多于平均值,而Tent映射的混沌變量分布較為均勻,在平均值附近波動,沒有較大落差;另外,多條混沌軌道的混沌遍歷性要優于單條混沌軌道[27]。因此,本文采用遍歷性更好的Tent混沌映射作為混沌變量發生器,并使用多條混沌軌道進行混沌搜索。 圖1 混沌映射遍歷性分析 信息論中,Shannon引入了信息熵的概念來度量離散事件的不確定度。本文受文獻[28]啟發,度量多樣性的種群熵描述如下: 1)設種群粒子集合為X={X1,X2,…,XM},粒子i表示成向量形式Xi=(Xi,1,Xi,2,…,Xi,N)T,其中:M為種群規模;N為問題維數。假定問題解空間的最大對角線的方向向量為V,長度為L。 2)計算每個粒子在V上的投影,即向量作內積Bi=VTXi(i=1,2,…,M),得到M個投影的值。 4)按照香農信源熵的定義計算在第t次迭代的種群分布熵: (13) 需要注意的是:這種定義下的種群分布熵在粒子分布絕對均勻時達不到理論上的最大值lnM。原因是即使粒子在解空間內均勻分布,但是此時解空間是一個N維的方體,向方體對角線方向向量作投影后落在等長度區間內的粒子數并不是均勻的,一般與空間的大小成正比。所以在種群隨機初始化時,種群分布熵一般達不到lnM。 平均粒距表達了種群各粒子之間分布的離散程度[26]。設解空間的最大對角線長度為L,M和N分別是種群規模和問題維數,則第t次迭代種群的平均粒距的計算公式如式(14)所示: (14) 其中: Xi, j(t)為粒子i的第j維坐標。平均粒距獨立于種群規模和問題維數,D(t)的值越大,各粒子較分散,種群多樣性較好;D(t)的值越小,粒子分布較集中,種群多樣性較差。 通常,種群多樣性越好,算法全局探索能力越強,但算法的局部搜索能力較弱。反之亦然。近年來已經有學者從種群多樣性的角度來動態調整粒子群算法的搜索過程,文獻[27]通過平均粒距來調整PSO算法的慣性權重w,在搜索過程中動態調整搜索方向提高了算法性能;但是只通過平均粒距來控制算法是有缺陷的,例如當遇到類似多峰問題時雖然平均粒距的值很小,但是粒子的多樣性卻很差。文獻[20]根據多樣性評價值,對慣性權重w動態控制,提出了基于反饋的自適應粒子群優化算法(Adoptive PSO algorithm based on feedback mechanism, APSO),具有較好的尋優能力和搜索速度。針對QPSO算法,從種群多樣性的角度提出了一種基于種群分布熵的CE系數α的自適應調整策略,并結合粒子分散程度,利用對平均粒距的評價在算法后期進行混沌搜索,即一種動態自適應混沌量子粒子群算法DACQPSO,并將DACQPSO算法應用到WSN覆蓋優化中。 在量子粒子群優化算法QPSO中,一般認為收斂性受CE系數α的取值影響。α取較大值時,算法具有較強的全局探索(exploration)能力,有利于跳出局部極值;α取較小值時,算法具有較強的局部開發(exploitation)能力,有利于精細化搜索。對于QPSO算法而言,算法收斂到全局最優的充分必要條件是α<1.781[29]。對CE系數α的設置通常采用線性遞減(Linear-Descending, LD)策略,其表達式為: (15) 其中:MAXTER為最大迭代次數;αmax和αmin為CE系數的迭代初始值和終止值。α從1.0線性減小到0.5一般都能取得比較好的效果。 CE系數α采用LD策略可以使得QPSO算法實現從廣泛探索到精細搜索的動態演化,完成對算法的控制,實驗結果表明α的這種設定策略具有普遍的指導性。雖然將α與迭代次數t建立強線性關系可以取得較好的效果,但是,群體內粒子的進化狀態與迭代次數t之間并不是這種直接的函數關系。由于粒子位置的更新具有隨機性,相鄰的兩代種群可能差異很大,此時需要跳躍性地控制進化趨勢才能避免種群極速跌入局部極值以致失去進化的動力。而相鄰兩次迭代的α的變化量Δα=(αmax-αmin)/MAXTER很小,不足以應付種群進化狀態的劇烈變化。LD策略沒有感知群體內各粒子進化態勢信息的能力,不能充分發揮QPSO算法的潛在性能。經過之前的分析容易知道,種群的多樣性可以在一定程度上描述群體內粒子的進化狀態,因此,本文從種群多樣性的角度出發,以種群分布熵作為多樣性評價指標,考察研究通過種群多樣性的變化來動態調整CE系數α的策略。 由于Sigmoid函數在線性與非線性之間具有極好的平衡性[30],將種群分布熵引入Sigmoid函數用于控制CE系數α,如式(16)所示: (16) 當kx<-9.903 438時,s(x)趨向于0;kx≥9.903 438時,s(x)趨向于1。DACQPSO算法的CE系數α定義如下: (17) (18) 一般在粒子群算法在搜索后期,各粒子要么已經聚集在局部極值點要么聚集在全局極值點。DACQPSO算法由于在前期已經采用了自適應搜索,在搜索后期,粒子以很大的概率聚集到了全局極值點的鄰域內。DACQPSO算法的混沌搜索思想為:算法按照式(17)定義的α(t)控制種群進化,完成粒子更新的基本操作,當種群平均粒距D(t)達到混沌搜索閾值c(c為一給定閾值,由具體問題測試確定)時,進行混沌搜索,實現混沌擾動。具體描述如下:隨機產生一個N維的向量Z0(t)=(Z0,1(t),Z0,2(t),…,Z0,N(t))T,其中,Z0, j(t)~U(0,1),j=1,2,…,N。以Z0(t)為初始值,每一維用Tent混沌方程式(12)分別迭代h次,產生N條混沌軌道,得到h個N維的混沌向量并構成一個混沌群,記作Ch。Ch群中第i個粒子表示為Zi(t)=[Zi,1(t),Zi,2(t),…,Zi,N(t)]T,i=1,2,…,h。根據式(19)、 (20)得到h個向量,這h個向量就是問題的h個解向量。 Yi(t)=gbest(t)±Ri(t)·Zi(t);i=1,2,…,h (19) Ri(t)=γRi-1(t);i=1,2,…,h;R1=R;0<γ≤1 (20) 由式(19)~(20)可以看出,混沌搜索的范圍可以覆蓋以gbest為中心、R為半徑的鄰域空間,并且可以由收縮因子γ控制搜索精度。在這h個解向量中確定最優的解向量,記為cbest(t)。按照式(21)和(22)更新pbestl(t+1)和gbest(t+1)。 pbestl(t+1)= gbest(t+1)= DACQPSO算法具體流程描述如下: 1)設置種群規模M、問題維數N、混沌搜索閾值c、混沌迭代次數h和收縮因子γ等參數的初始值;隨機初始化種群各粒子,并計算每個粒子的個體最優pbest(t)和全局最優gbest(t)。 2)按式(13)計算本次迭代的種群分布熵E(t),并根據式(17)計算CE系數α(t)。 3)根據式(10)計算平均最好位置mbest(t)。并根據式(8)~(9)更新粒子i的吸引子Qi(t)和粒子位置Xi(t+1)。 4)計算各粒子的適應度,根據式(6)和(7)更新各粒子的個體最優pbest(t+1)和全局最優gbest(t+1)。 5)根據式(14)計算本次迭代的種群平均粒距D(t),若D(t)≤c,則轉入6)進行混沌搜索;否則轉入7)。 7)若未達到終止條件則返回2);否則,算法結束。 假設監測區域為20 m×20 m的平面,將該區域離散化成20×20個像素點。在該區域內部署24個同構的傳感器節點。所有節點的感知半徑Rs=2.5 m,通信半徑Rc=2Rs=5 m[31]。節點概率感知模型式(1)中的參數λ1=1,λ2=0,β1=1,β2=1.5,re=1.25 m,Prth=0.6。算法最大迭代次數MAXTER=150。設置式(17)中的αmax=0.95,αmin=0.4。混沌迭代次數h=50,混沌搜索最大半徑R=5;收縮因子k=0.85。種群規模M=15,粒子表示為Xi=(xi,1,yi,1,xi,2,yi,2,…,xi,24,yi,24)T,i=1,2,…,15,其分量xi, j、yi, j表示傳感器節點i的位置坐標。由于解空間是個48維的方體,經前期大量數據測試,種群隨機初始化的種群分布熵取其均值,lnM=0.935。同時受MAXTER的影響將式(18)更新為: (23) 使用主頻3.2 GHz的主機,Windows 7旗艦版操作系統,在Matlab 2015b環境下進行仿真實驗。 DACQPSO算法中最重要的參數就是CE系數α和混沌搜索閾值。而混沌搜索閾值受問題規模、適應度函數和問題類型等眾多因素的影響,混沌搜索閾值的選取是一個不確定優化問題,由具體問題給定,不是本文的研究重點。本節將研究DACQPSO算法在不同參數設置下的性能,并作對比分析。 為了驗證CE系數α對算法的影響,將α分別取固定值從1~0.1,以式(4)定義的網絡覆蓋率為適應度函數f,分別在每個固定的α下對目標問題進行10次優化,每次優化迭代100次,結果如表1所示。為了考察不同的α值對算法性能的影響是否有顯著的差異,對目標函數在不同α水平下的結果作單因素方差分析,結果如表2所示。 表1 不同CE系數 α 值下網絡覆蓋率的優化結果 表2 單因素方程分析 圖2 兩種算法在各混沌閾值c下的網絡覆蓋率對比 表2中:SS為離差平方和,df為自由度,MS為均方,F為F值,P-value為F分布的概率,F-crit為F的臨界值。由于F=33.812>F-crit=1.985 6,故在顯著性水平0.05條件下認為不同的α值對算法性能的影響存在顯著的差異。方差分析的結果表明:CE系數α的取值對QPSO算法的性能有很大的影響,在算法執行過程中合理地調整α對提高算法性能意義重大。 為了研究混沌量子粒子群CQPSO算法和DACQPSO算法在不同的混沌搜索閾值下對目標問題的優化性能,設置不同的c值,分別在每個c下對目標問題進行10次優化,每次優化的最大迭代次數為150,結果如表3所示。為了全面考察閾值的影響,除覆蓋率外還增加了均勻度、覆蓋效率、平均移動距離、最優迭代次數、計算耗時5個指標。表3中的數據為優化結果的平均。 從表3可以看出,混沌搜索閾值對CQPSO算法和DACQPSO算法的優化性能都有影響。從整體上看,在每個實驗選取的c值下,DACQPSO算法在除算法耗時以外的所有指標上都要優于CQPSO算法。圖2顯示了在不同混沌搜索閾值下CQPSO算法和DACQPSO算法的優化結果在覆蓋率指標上的情況。從圖2可以看出兩種算法當c值在取0.005 5附近時算法能發揮最佳性能。c值過小,種群粒子過分聚集混沌搜索只能完成精細搜索,很難跳出目前的極值;c值過大,混沌擾動對量子粒子群內在尋優機制產生較大干擾,不利于全局搜索且大幅增加了計算消耗。因此,本文實驗中的混沌搜索閾值c取0.005 5。 圖3 不同算法優化后的節點分布 算法閾值c覆蓋率/%均勻度覆蓋效率/%平均移動距離/m最優迭代次數耗時/sCQPSODACQPSO0.001584.90000.550672.06549.7973144.7000564.88900.002584.42500.556971.66229.6788143.4000562.30580.003583.65000.545971.00439.8999145.3000629.68220.004585.22500.571272.34129.7401143.3000584.76300.005585.47500.501172.553410.1080144.4000639.76310.006582.32500.582369.87969.9210145.6000596.14610.007585.50000.541272.57479.9552141.7000619.36470.008584.45000.568771.68349.7212147.1000572.68600.001585.57500.523172.63839.5805127.9000836.27440.002585.97500.530372.97789.7303127.7000842.22090.003585.15000.521072.27769.5648120.1000957.34080.004585.47500.537172.55349.4789125.7000890.53120.005586.30000.567873.25379.6779125.2000915.40010.006584.80000.550471.98059.6891121.2000860.22180.007586.00000.512972.99919.6918122.7000784.95240.008585.77500.531672.80819.7739122.5000938.5698 為了驗證DACQPSO算法的性能,選取了標準粒子群算法SPSO、量子粒子群算法QPSO、混沌量子粒子群算法CQPSO與DACQPSO算法作對比實驗。圖3為經過不同算法迭代150次優化后傳感器節點的分布情況。可以看出,SPSO算法優化效果較差,經過DACQPSO優化后的節點分布更為均勻,WSN的覆蓋范圍更大。圖3中:“+”表示傳感器節點位置;圓圈表示節點感知半徑Rs;“—”連接的節點構成的集合構成一個最小生成樹,以保持WSN的連通性。這四種算法的尋優收斂曲線如圖4所示。其中,SPSO、QPSO、CQPSO和DACQPSO算法優化后的網絡覆蓋率分別為81%、83%、86.25%和88%。在WSN網絡覆蓋率優化上,DACQPSO算法相對于其他算法分別提高了7、5和1.75個百分點。 為了全面地評價算法的性能,對四種算法分別進行20次WSN覆蓋優化,每次優化算法迭代150次。各覆蓋評價指標數據取平均值,如表4所示。 分析表4數據可以得出:在WSN覆蓋優化最重要的性能評價指標網絡覆蓋率上,DACQPSO算法優勢明顯,相對于其他三種算法,將網絡覆蓋率分別提高了2.825、2.25和1.625個百分點。傳感器節點的覆蓋效率也最高,比其他算法分別提高了2.397 9、1.909 8和1.379 3個百分點,提高了節點的利用率。在最優迭代次數指標上,比其他算法分別提前了30.6、39.6和38.0次,說明算法收斂更快。在均勻度和最優平均距離兩個指標上四種算法大致相當,無明顯優勢。在算法耗時指標上,DACQPSO算法的耗時幾乎是其他三種算法的2倍。這是因為DACQPSO算法需要計算種群分布熵和平均粒距這兩個種群多樣性指標,增加了計算消耗。隨著軟硬件水平的發展,算法耗時問題可以得到解決。 表4 四種算法優化效果對比 圖4 四種對比算法的收斂曲線 通過研究種群多樣性與粒子群算法進化的關系,將種群分布熵和平均粒距兩個指標引入混沌量子粒子群優化算法中,提出了一種動態自適應的混沌量子粒子群優化算法——DACQPSO,該算法通過種群多樣性的變化感知種群的進化態勢,動態自適應地控制算法的優化進程,實現了全局搜索與局部搜索的平衡,具有較強的自適應能力。將算法應用于WSN的覆蓋優化中,仿真實驗結果表明,DACQPSO算法提高了WSN的覆蓋率和覆蓋效率,提高了收斂速度,是一種有效的WSN覆蓋優化算法。 如果找到一種理想的種群分布熵的計算模型,可以度量任意維度空間內粒子分布的均勻性,那么DACQPSO的適應性將會更加出色。 參考文獻(References) [1] YOON Y, KIM Y-H. An efficient genetic algorithm for maximum coverage deployment in wireless sensor networks [J]. IEEE Transactions on Cybernetics, 2013, 43(5): 1473-1483. [2] AKBARZADEH V, GAGNE C, PARIZEAU M, et al. Probabilistic sensing model for sensor placement optimization based on line-of-sight coverage [J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(2): 293-303. [3] 賈杰,陳劍, 常桂然, 等. 無線傳感器網絡中基于遺傳算法的優化覆蓋機制[J]. 控制與決策, 2007, 22(11): 1289-1292.(JIA J, CHEN J, CHANG G R, et al. Optimal coverage scheme based on genetic algorithm in wireless sensor networks [J]. Control and Decision, 2007, 22(11): 1289-1292.) [4] 于文杰, 李迅波, 羊行, 等. 外推人工蜂群算法在WSN部署優化中的應用研究[J]. 儀表技術與傳感器, 2017(6): 158-160.(YU W J, LI X B, YANG H, et al. Extrapolation artificial bee colony algorithm research on deployment optimization in wireless sensor network [J]. Instrument Technique and Sensor, 2017(6): 158-160.) [5] KUNDU R, DAS S, MUKHERJEE R, et al. An improved particle swarm optimizer with difference mean based perturbation [J]. Neurocomputing, 2014, 129(129): 315-333. [6] WANG X, WANG S, MA J J. An improved co-evolutionary particle swarm optimization for wireless sensor networks with dynamic deployment [J]. Sensors, 2007, 7(3): 354-370. [7] 馮琳, 冉曉旻, 梅關林. 基于改進粒子群算法的無線傳感網絡覆蓋優化[J]. 太赫茲科學與電子信息學報, 2015, 13(3): 486-490.(FENG L, RAN X M, MEI G L. WSN coverage optimization by improved artificial PSO algorithm [J]. Journal of Terahertz Science and Electronic Information Technology, 2015, 13(3): 486-490.) [8] 劉維亭, 范洲遠. 基于混沌粒子群算法的無線傳感器網絡覆蓋優化[J]. 計算機應用, 2011, 31(2): 338-340.(LIU W T, FAN Z Y. Coverage optimization of wireless sensor networks based on chaos particle swarm algorithm [J]. Journal of Computer Applications, 2011, 31(2): 338-340.) [9] 吳意樂, 何慶, 徐同偉. 改進自適應粒子群算法在WSN覆蓋優化中的應用[J]. 傳感技術學報, 2016, 29(4): 559-565.(WU Y L, HE Q, XU T W. Application of improved adaptive particle swarm optimization algorithm in WSN coverage optimization [J]. Chinese Journal of Sensors and Actuators, 2016, 29(4): 559-565.) [10] 王偉, 朱娟娟, 萬家山, 等. 基于混沌量子粒子群算法的無線傳感器網絡覆蓋優化[J]. 傳感技術學報, 2016, 29(2): 290-296.(WANG W. ZHU J J, WAN J S, et al. Coverage optimization of wireless sensor networks based on chaotic quantum-behaved particle swarm algorithm [J]. Chinese Journal of Sensors and Actuators, 2016, 29(2): 290-296.) [11] 張娟. 基于粒子群優化算法的無線傳感器網絡節能覆蓋研究[D]. 上海: 華東理工大學, 2014: 9-10.(ZHANG J. Energy saving coverage control study of wireless sensor networks based on particle swarm optimization algorithm [D]. Shanghai: East China University of Science and Technology, 2014: 9-10.) [12] 曹峰, 劉麗萍, 王智. 能量有效的無線傳感器網絡部署[J]. 信息與控制, 2006, 35(2): 147-153.(CAO F, LIU L P, WANG Z. A new energy-efficient WSN deployment algorithm [J]. Information and Control, 2006, 35(2): 147-153.) [13] 林祝亮. 基于粒子群算法的無線傳感網絡覆蓋問題優化策略研究[D]. 杭州: 浙江工業大學, 2009: 14-16.(LIN Z L. Coverage optimization strategy of wireless sensor networks based on particle swarm optimization [D]. Hangzhou: Zhejiang University of Technology, 2009: 14-16.) [14] KENNEDY J, EBERHARR R. Particle swarm optimization [C]// Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ: IEEE, 1995: 1942-1948. [15] BERGH F V D. An analysis of particle swarm optimizers [D]. Pretoria: University of Pretoria, 2001: 78-126. [16] CLERC M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization [C]// Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 1999: 1951-1957. [17] KENNEDY J. Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance [C]// Proceedings of the 1999 Congress on Evolutionary Computation, Piscataway, NJ: IEEE, 1999: 1931-1938. [18] LOVBJERG M, RASUSSEN T K, KRINK T. Hybrid particle swarm optimizer with breeding subpopulations [EB/OL]. [2017- 09- 20]. http: //pdfs.semanticscholar.org/1e4c/ddd9d4b89a9dbdf854aaf84b584ba47386ab.pdf. [19] 劉宇, 覃征, 史哲文. 簡約粒子群優化算法[J]. 西安交通大學學報, 2006, 40(8): 883-887.(LIU Y, QIN Z, SHI Z W. Compact particle swarm optimization algorithm [J]. Journal of Xi’An Jiaotong University, 2006, 40(8): 883-887.) [20] 俞歡軍, 張麗平, 陳德釗, 等. 基于反饋策略的自適應粒子群優化算法[J]. 浙江大學學報(工學版), 2005, 39(9): 1286-1291.(YU H J, ZHANG L P, CHEN D Z, et al. Adaptive particle swarm optimization algorithm based on feedback mechanism [J]. Journal of Zhejiang University (Engineering Science), 2005, 39(9): 1286-1291.) [21] SUN J, FENG B, XU W. Particle swarm optimization with particles having quantum behavior[C]// CEC 2004: Proceedings of the 2004 Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2004: 325-331. [22] 孫俊. 量子行為粒子群優化算法研究[D]. 無錫: 江南大學, 2009: 9-83.(SUN J. Particle swarm optimization with particle having quantum behavior [D]. Wuxi: Jiangnan University, 2009: 9-83.) [23] SUN J, XU W, FENG B. A global search strategy of quantum-behaved particle swarm optimization [C]// Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems. Piscataway, NJ: IEEE, 2004: 111-116. [24] 孫俊, 方偉, 吳小俊. 量子行為粒子群優化: 原理及其應用[M]. 北京: 清華大學出版社, 2011: 9-68.(SUN J, FANG W, WU X J. Quantum behaved particle swarm optimization: principle and application [M]. Beijing: Tsinghua University Press, 2011: 9-68.) [25] 高尚, 楊靜宇. 混沌粒子群優化算法研究[J]. 模式識別與人工智能, 2006, 19(2): 266-270.(GAO S, YANG J Y. Research on chaos particle swarm optimization algorithm [J]. Pattern Recognition and Artificial Intelligence, 2006, 19(2): 266-270.) [26] 劉軍民, 高岳林. 混沌粒子群優化算法[J]. 計算機應用, 2008, 28(2): 322-325.(LIU J M, GAO Y L. Chaos particle swarm optimization algorithm [J]. Journal of Computer Applications, 2008, 28(2): 322-325.) [27] 陳如清, 俞金壽. 混沌粒子群混合優化算法的研究與應用[J]. 系統仿真學報, 2008, 20(3): 685-688.(CHEN R Q, YU J S. Study and application of chaos-particle swarm optimization-based hybrid optimization algorithm [J]. Journal of System Simulation, 2008, 20(3): 685-688.) [28] 湯可宗, 吳雋, 趙嘉. 基于多樣性反饋的自適應粒子群優化算法[J]. 計算機應用, 2013, 33(12): 3372-3374.(TANG K Z, WU J, ZHAO J. Adaptive particle swarm optimization algorithm based on diversity feedback [J]. Journal of Computer Applications, 2013, 33(12): 3372-3374.) [29] SUN J, WEI F, WU X, et al. Quantum-behaved particle swarm optimization: analysis of individual particle behavior and parameter selection [J]. Evolutionary Computation, 2012, 20(3): 349-393. [30] 王玉冰, 王錦江, 王穎龍. 一種基于種群熵的自適應遺傳算法[J]. 微計算機信息, 2010, 26(1): 32-34.(WANG Y B, WANG J J, WANG Y L. An colony entropy-based adaptive genetic algorithm [J]. Microcomputer Information, 2010, 26(1): 32-34.) [31] ZHANG H, HOU J. Maintaining sensing coverage and connectivity in large sensor networks [J]. Ad Hoc & Sensor Wireless Networks, 2005, 1(2): 89-124. This work is partially supported by the National Natural Science Foundation of China (61402013).1.2 覆蓋評價指標
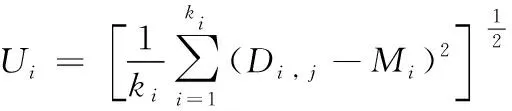
2 量子粒子群優化算法

3 混沌搜索
4 多樣性測度
4.1 種群熵
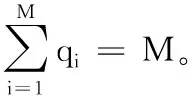
4.2 平均粒距
5 動態自適應混沌量子粒子群優化算法
5.1 收縮擴張系數α的自適應控制

5.2 DACQPSO算法的混沌搜索機制
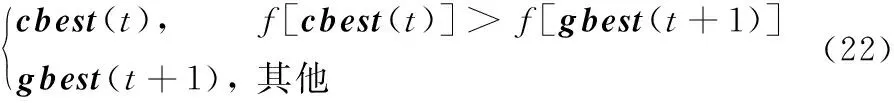
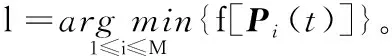
5.3 算法流程
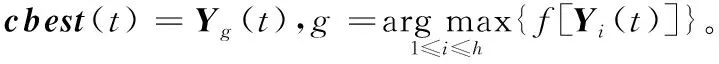
6 仿真實驗與分析
6.1 仿真環境與參數設置
6.2 參數設置對算法性能的影響分析
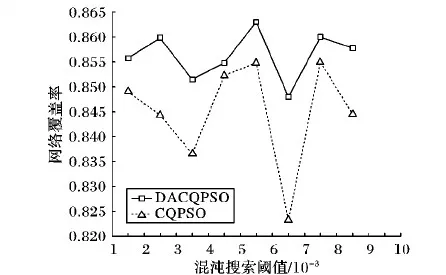
6.3 實驗結果與分析
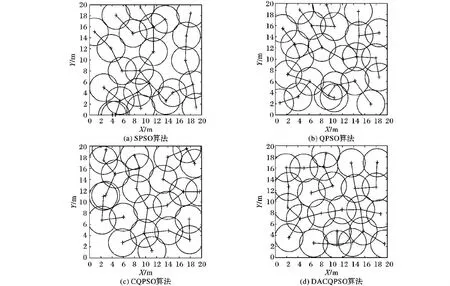

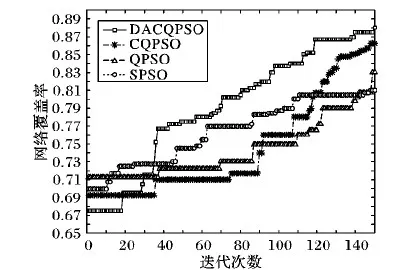
7 結語

