高速受電弓作用下接觸網整體吊弦動態力研究

陳立明

(中國鐵道科學研究院 標準計量研究所，北京 100015)

接觸網是電氣化鐵路的關鍵組成部分，為列車運行提供動力[1]。整體吊弦是接觸網安全運行的關鍵零部件，是接觸線與承力索間振動和力的傳遞者[2]。隨著列車速度的不斷提高，對接觸網整體吊弦可靠性也提出了更高的要求。如我國武廣客運專線設計時速為350 km，運行不久后便發現整體吊弦出現斷絲、斷股的現象[3]。受電弓在沿著接觸線運行的過程中，會引起接觸線的抬升和接觸壓力的變化[4]，進而引起整體吊弦的壓縮和拉伸及其受力的變化。受力是導致整體吊弦斷絲、斷股的最本質因素。因此，研究受電弓作用下整體吊弦的動態力對分析其失效原因有重要意義。

研究整體吊弦動態力之前需要對接觸網進行找形分析，以確定承力索弛度、整體吊弦長度等關鍵參數。最簡單快速的找形方法為拋物線法[5],該方法將承力索的初始形狀簡化為二次拋物線，從而確定整體吊弦的長度；但該方法未考慮承力索馳度及接觸網結構間的力學平衡關系，計算精度不夠。為克服這類缺點，方巖等人[6]提出了分模法，該方法能夠獲得足夠的精度，但卻將接觸網分解成2個子系統，不利于后續的動態求解。周寧等人[7]提出了負弛度法，該方法給承力索預留一定的負弛度，然后施加重力和補償張力，并將計算結果與設計要求對比后，再重新設置負弛度，進行迭代計算，最終得到滿足設計要求的接觸網初始形態。

研究國內外學者對弓網系統動態性能的已經做了大量工作。Park等[8]對受電弓與接觸網相互作用方式進行仿真分析，得到了在該仿真模型下的弓網動態響應曲線。Metrikine等[9]將受電弓的作用簡化成均勻移動的點荷載，并對移動載荷下弓網動態行為進行分析。張衛華等[10]對接觸網振動模態進行了分析，在此基礎上建立了接觸網運動微分方程。

然而，針對受電弓經過時整體吊弦動態力的研究相對較少。韓國Cho等[11-12]采用實測和仿真的方法，研究受電弓以160 km·h-1經過時Honam高速鐵路整體吊弦的動態力，并提出了一種實測整體吊弦疲勞壽命的模型，然而其中的接觸網模型和列車速度均與我國存在較大差距。德國力倍公司建立了整體吊弦振動試驗臺，在實驗室模擬整體吊弦的振動過程，但未對整體吊弦的動態力進行定量的研究[13]。

本文以我國高速鐵路廣泛采用的彈鏈型接觸網為研究對象，現場測量受電弓通過過程中整體吊弦的動態抬升量，以此作為有限元仿真的初始載荷，模擬受電弓經過時接觸網的動態行為，得到了受電弓作用下整體吊弦的動態力，為研究整體吊弦失效機理提供依據。

1 現場測試

接觸網系統為帶高壓電系統，實際測量整體吊弦的動態力不容易實現，故本文以實測的整體吊弦抬升量曲線為動態載荷，利用有限元仿真分析受電弓通過時整體吊弦的動態力。采集設備由硬件和軟件兩部分組成。其中，硬件包括圖像采集器(Baumer optronics GmbH，HXG20)、測量鏡頭(Samyang Ltd，NAF800mm F8.0)以及測距儀、風速儀、測速儀等設備，軟件為C++語言編寫的應用軟件，包括數據采集和數據處理兩部分。數據處理軟件通過標定距離像素比例，建立圖像像素與結構實際高度的對應關系，并通過計算受電弓經過時像素的變化計算出整體吊弦與接觸線連接處的抬升量。

雙受電弓工作的高速列車以時速250 km(測量時速)經過測試點時，整體吊弦的抬升量如圖1所示。由圖1可以看出：前受電弓經過時引起的整體吊弦最大抬升量為59.04 mm，后受電弓經過時引起的整體吊弦最大抬升量為79.60 mm。

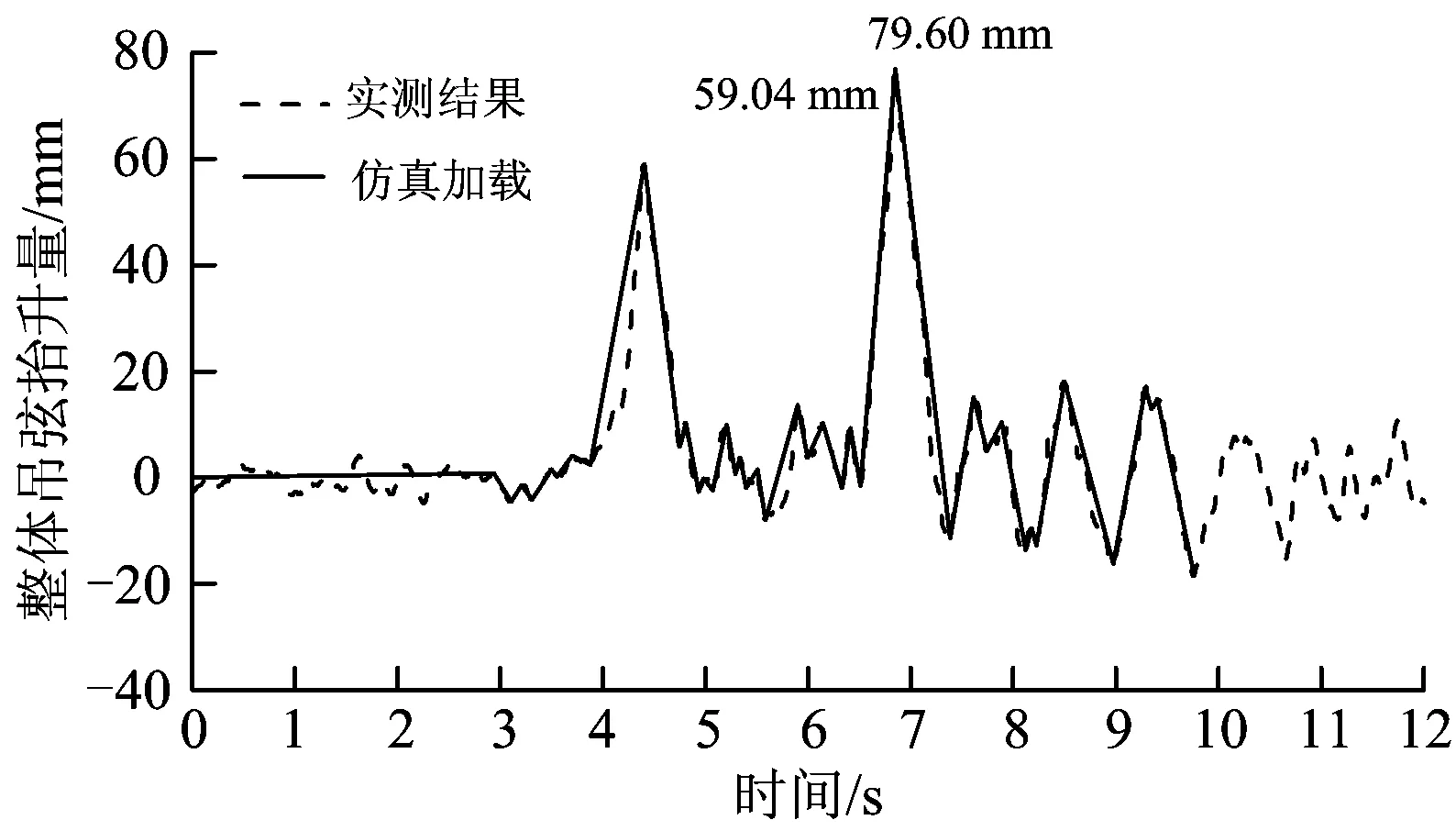
圖1 高速列車以時速250 km經過時整體吊弦的抬升量

2 有限元模型建立

2.1 接觸網結構模型

目前我國高速鐵路接觸網普遍采用全補償彈性鏈型懸掛結構，其結構模型如圖2所示。圖中：x為順線路方向；y為順整體吊弦方向；▲表示y向約束和轉動約束；■表示只有y向約束；1-1#，1-2#，…，3-5#為整體吊弦從左向右的編號(第1個數字表示所在跨的編號，第2個數字表示跨內整體吊弦的編號)；Fc, x為承力索的補償張力；Fj, x為接觸線的補償張力；Ft, x為彈性吊索張力。承力索為120型銅鎂合金絞線；接觸線為150型銅鎂合金接觸線；彈性吊索的長度為13 m、橫截面積為35 mm2；吊弦的橫截面積為10 mm2。

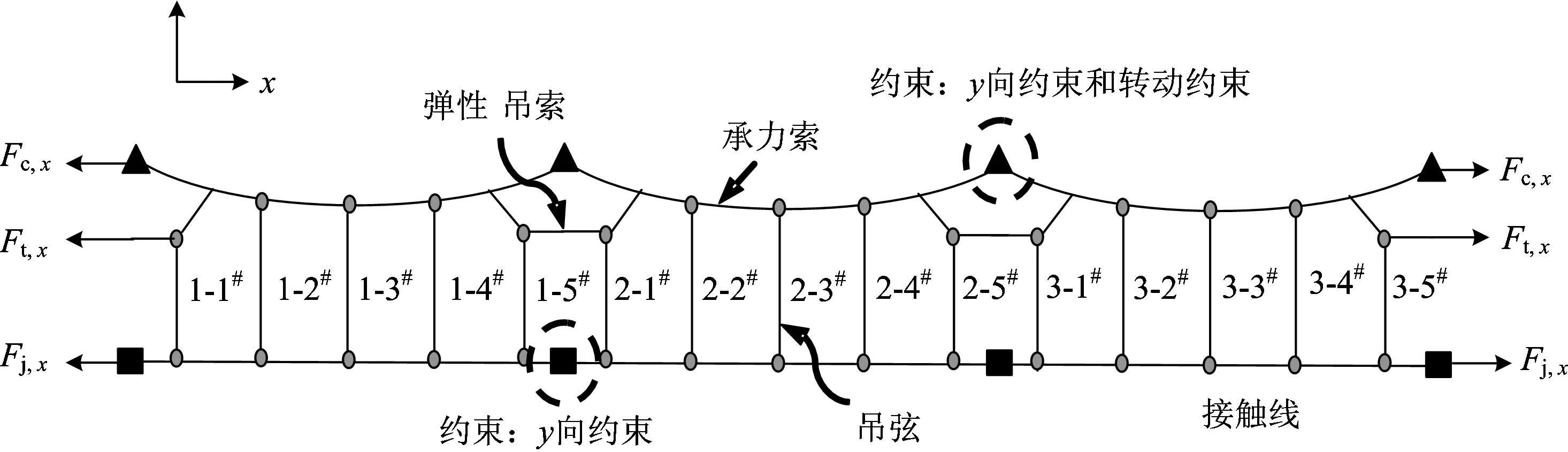
圖2 接觸網的結構模型

2.2 邊界條件

為真實模擬接觸網的安裝施工過程，依據其施工設計條件設定力的邊界條件，即Fc, x=21 kN，Fj, x=30 kN，Ft, x=3.5 kN。承力索與掛臂連接處的垂直位移為0，無相對轉動。接觸線與定位器連接處的垂直位移為0，可以平面轉動。承力索、接觸線、彈性吊索受補償張力作用。

2.3 接觸網有限元模型

在接觸網眾多模型中，代表性的有集中質量模型、梁模型以及與頻率有關的link模型[14]。梁單元(beam188)基于鐵木辛柯梁結構理論，考慮了彎曲變形，能夠較好地模擬接觸網的靜態或瞬態幾何大變形，因此在ANSYS有限元分析軟件中采用梁單元對承力索、彈性吊索、接觸線進行模擬。采用索單元(link180)對其接觸網進行模擬，將其質量均勻分布于單元內，設置其壓縮剛度為0。

本文僅對接觸網的典型結構進行分型，因此分析過程中建立3跨接觸網有限元模型，且僅對第2跨(即中間跨)接觸網有限元模型進行分析，第2跨接觸網有限元模型如圖3所示。分析過程中網格劃分單元尺寸分別為：接觸線0.5 m，承力索0.25 m，彈性吊索0.25 m。接觸線、承力索、整體吊線、彈性吊索的密度分別為8 940，8 875，9 000和8 857 kg·m-3，由于所有材料均認為是各向同性彈性材料，故其彈性模量和泊松比相同，分別為120 GPa和0.33。

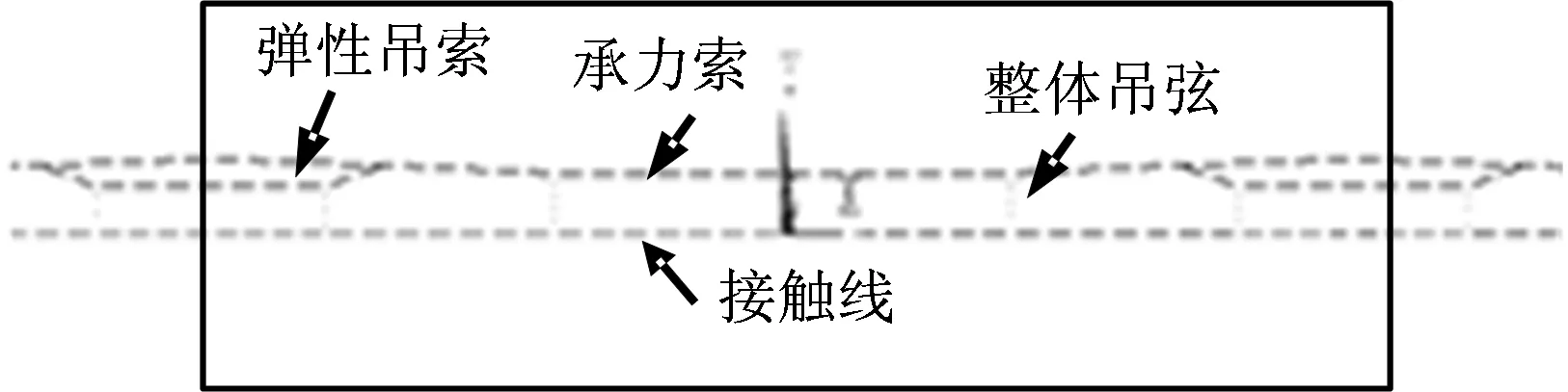
圖3 第2跨接觸網有限元模型

3 靜態找形分析及結果

因接觸網在自重作用下呈垂線型，則采用負弛度法對接觸網進行找形分析時給承力索預留一定的負弛度，然后施加重力和補償張力，在經過幾次迭代計算后，使接觸線保持水平，且同時滿足彈性吊索張力條件，最終得到接觸網的初始形態。

根據目前安裝規范要求，采用如下內容作為滿足接觸網找形分析的條件：①50 m跨內接觸線高差小于0.01 m；②彈性吊索張力為(3 500±175)N。

找形分析后第2跨接觸線高差小于0.01 m，彈性吊索張力為3 541.2 N，滿足找形分析的條件承力索弛度如圖4所示。由圖4可以看出承力索為拋物線結構，且關于2-3#整體吊線對稱。

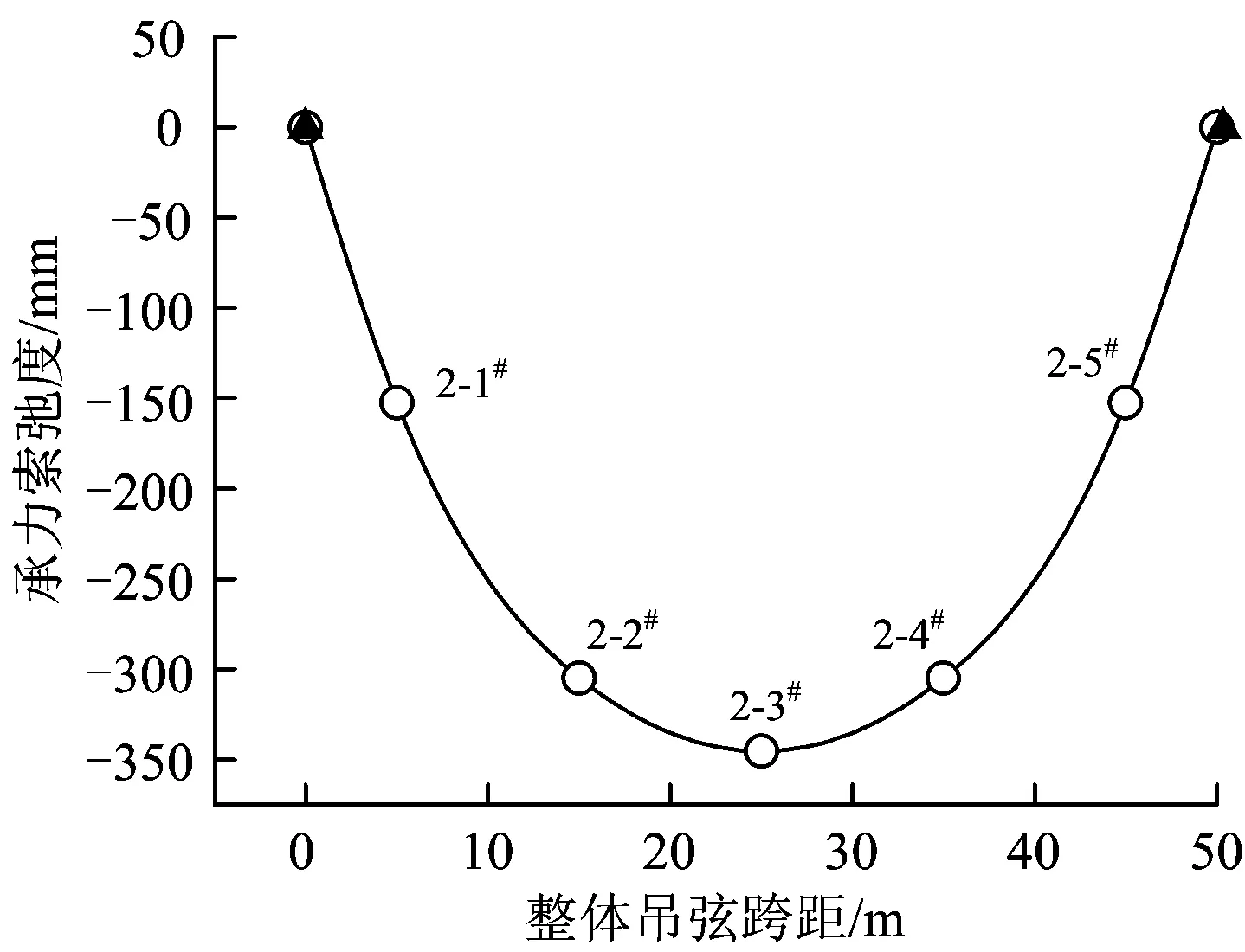
圖4 第2跨承力索的馳度分析結果

找形分析后通過有限元計算得到第2跨整體吊弦的拉力和應力見表1。由表1可知：整體吊弦2-1#與2-5#位置對稱，整體吊弦2-2#與2-4#位置對稱。

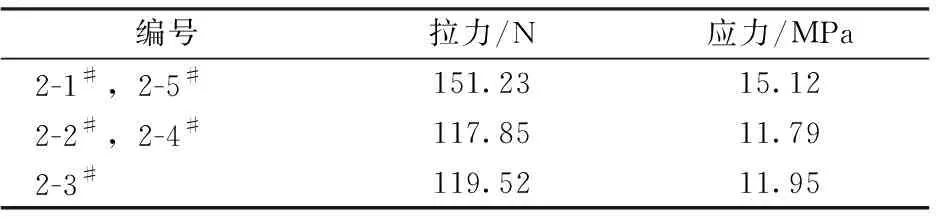
表1 第2跨整體吊弦的拉力和應力

4 瞬態動力學分析

實際情況下，接觸網通常受風、腐蝕、溫度等環境載荷的影響，分析較為復雜。為簡化分析，僅考慮補償張力和重力對接觸網的影響，忽略環境因素。同時，為提高計算精度，研究過程采用幾何大變形進行結構分析，在處理幾何非線性問題時，采用Newmark積分算法對動力學方程進行求解。由表1可知，2-1#與2-5#，2-2#與2-4#整體吊弦的力學性能一致，因此下文僅給出2-3#，2-2#和2-1#整體吊弦的分析結果。

4.1 受電弓經過2-3#整體吊弦時的動態力

接觸網第2跨中的整體吊弦呈對稱分布，因此僅提取前半跨結果，2-1#， 2-2#，2-3#整體吊弦的動態力如圖5所示。由圖可以看出：2-3#整體吊弦受力有較大幅度的變化，最大值為719.51 N，約為其靜態受力(119.52 N)的6倍。與2-3#整體吊弦相比，2-2#和2-1#整體吊弦力的明顯減小，但始終保持受拉狀態。

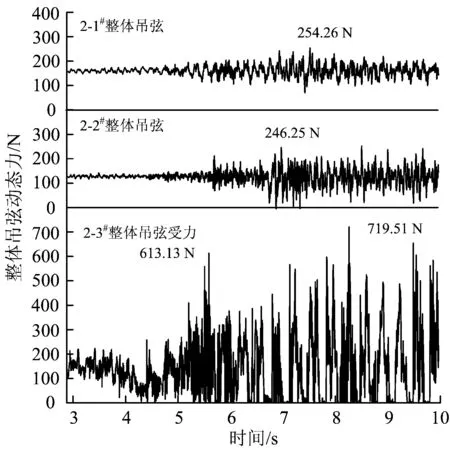
圖5 受電弓經過2-3#整體吊弦時的動態力

受電弓經過2-3#整體吊弦時，通過計算整體吊弦上端點和下端點的垂直位移差值，可以求得整體吊弦的拉伸、壓縮情況，上下端點垂直位移差值為正時表示整體吊弦拉伸，為負時表示整體吊弦壓縮，結果如圖6所示。圖中：a為受電弓經過時的起始點；b，c，d和e為受電弓經過時的4個典型位置。當受電弓經過時，整體吊弦經歷了數次壓縮，其中最大壓縮幅值為25.75 mm；與整體吊弦的壓縮量相比，整體吊弦的拉伸量極小，最大為0.706 mm。

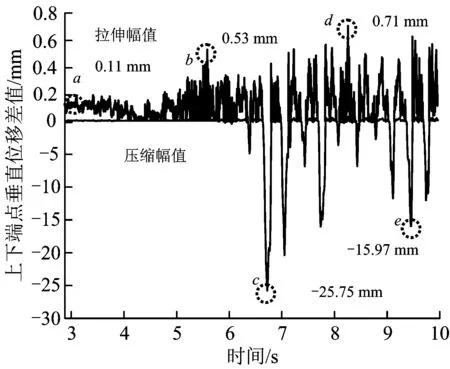
圖6 2-3#整體吊弦的拉伸/壓縮情況

受電弓經過2-3#整體吊弦時5個典型位置處的吊弦力、垂直位移差值以及抬升量結果見表2。表中，整體吊弦抬升量為整體吊弦下端點離開初始位置的位移，其為正值表示向上的偏移量，為負值表示向下的偏移量。由表2可以看出：整體吊弦拉伸時，其承受拉力；壓縮時，其承受的壓力為0。

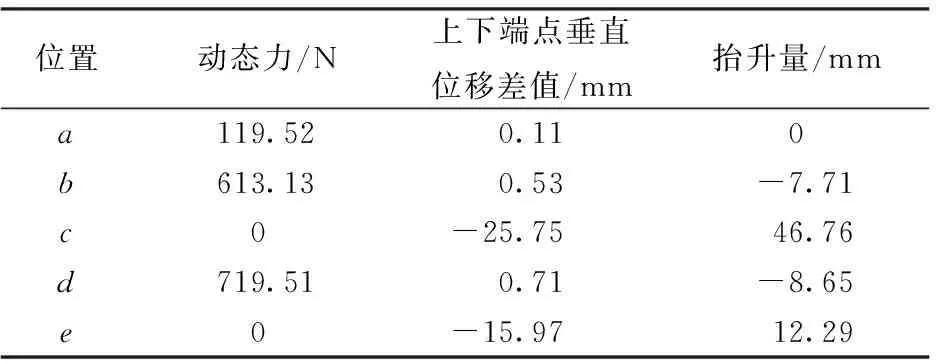
表2 受電弓經過2-3#整體吊弦時結果

4.2 受電弓經過2-2#整體吊弦時的動態力

受電弓經過時，2-2#整體吊弦時及與之相鄰整體吊弦的受力情況如圖7所示。由圖7可以看出：

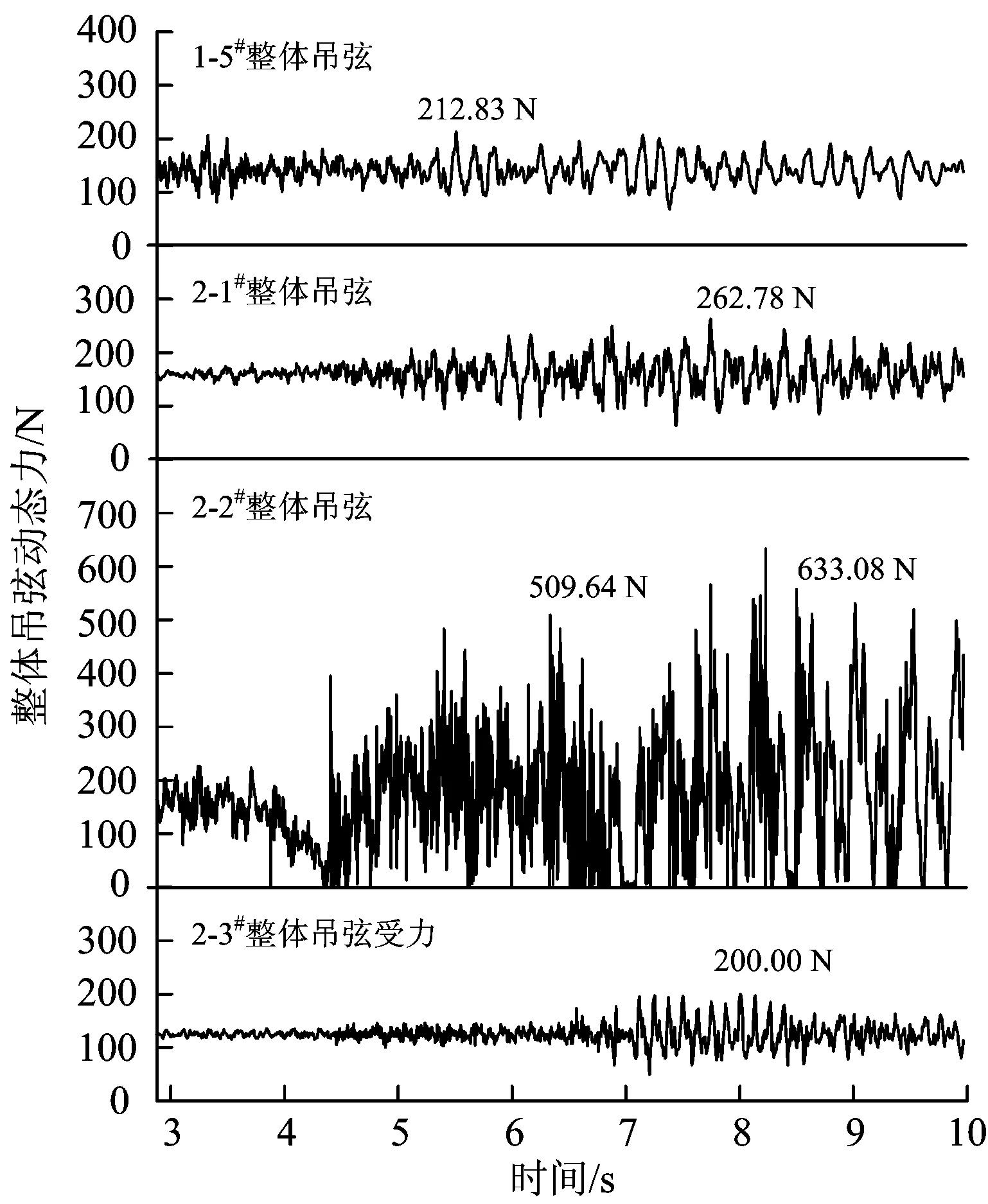
圖7 受電弓經過2-2#整體吊弦時的動態力

2-2#整體吊弦受力有較大幅度的變化，最大為633.08 N；2-1#與2-3#整體吊弦相比吊弦力的變化幅度較大，說明2-1#整體吊弦更容易受到影響；受電弓經過2-2#整體吊弦的整個過程中，2-1#和2-3#整體吊弦均始終保持受拉狀態，沒有經歷壓縮過程。1-5#整體吊弦距離2-2#整體吊弦位置較遠，受到的影響相對較小。

受電弓經過2-2#整體吊弦時其拉伸、壓縮情況如圖8所示。由圖8可以看出：2-2#整體吊弦發生2次較大幅值的壓縮，壓縮幅值分別為15.79和7.94 mm，其余時間段內整體吊弦處于拉伸狀態，最大拉伸幅值為0.57 mm。

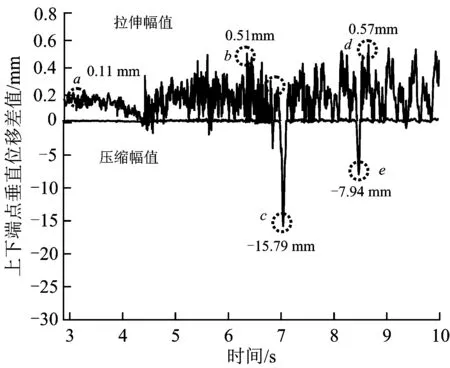
圖8 2-2#整體吊弦的拉伸/壓縮情況

受電弓經過2-2#整體吊弦時不同典型位置處的吊弦力、垂直位移差值以及抬升量結果見表3。由表3可以看出：a處為整體吊弦的靜態結果，靜態時整體吊弦承受拉力為119.52 N，整體吊弦拉伸量為0.11 mm。

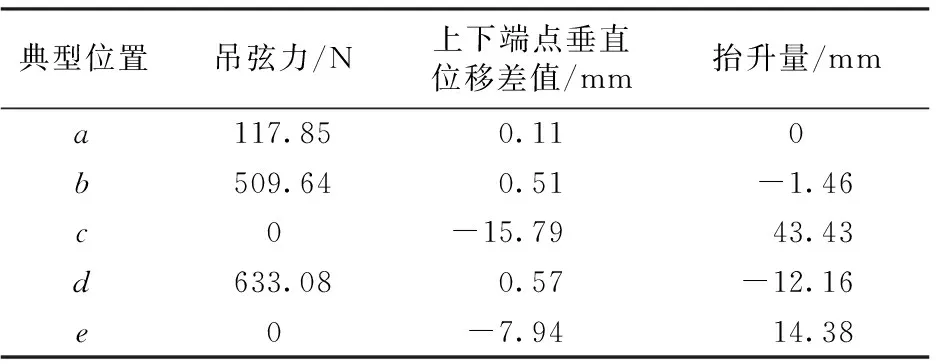
表3 受電弓經過2-2#整體吊弦時結果

4.3 受電弓經過2-1#整體吊弦時的動態力

受電弓經過時，2-1#整體吊弦時及與之相鄰整體吊弦的受力情況如圖9所示。由圖9可以看出：受電弓經過時，2-1#整體吊弦受力發生了較大幅度的變化,其中最大值為727.40 N，而1-5#，2-2#整體吊弦的吊弦力及其變化幅值明顯減小，2-3#整體吊弦基本不受影響。

圖9 受電弓經過2-1#整體吊弦時的動態力

受電弓經過2-1#整體吊弦時引起該整體吊弦的拉伸/壓縮幅值如圖10所示。由圖10可以看出：2-1#整體吊弦的最大壓縮幅值為27.85 mm。

圖10 2-1#整體吊弦的拉伸/壓縮情況

受電弓經過1#整體吊弦時不同典型位置處吊弦力、上下端點垂直位移差值以及抬升量結果見表4。由表4可以看出：a時刻為整體吊弦靜態時結果，靜態時整體吊弦承受拉力為151.23 N，整體吊弦拉伸量為0.11 mm。

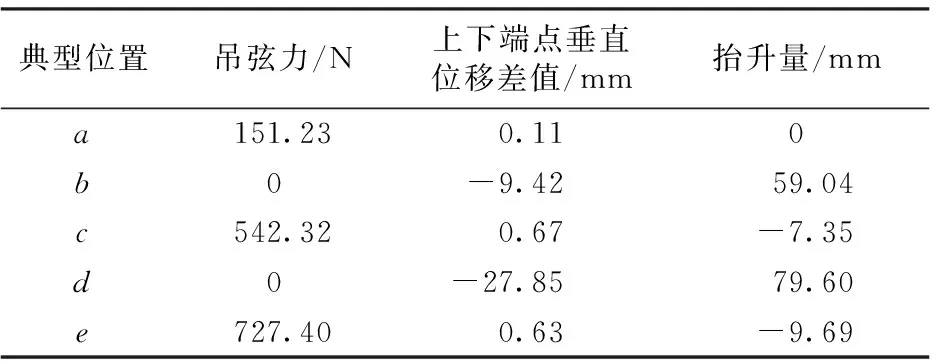
表4 受電弓經過2-1#整體吊弦時結果

4.4 對比分析

通過對接觸網的靜態找形分析以及受電弓經過整體吊弦時的瞬態動力學分析，可以發現接觸網是低剛度、低頻率的振動系統，因而很容易產生共振。受電弓與接觸線相對滑動，由于接觸力的作用會使整體吊弦迅速抬升，產生彎曲變形，然后迅速下降，在整體吊弦上產生拉應力。這種振動效益會通過承力索、接觸線傳遞到相鄰的整體吊弦，引起其他整體吊弦的抬升和吊弦力的變化。由于整體吊弦在接觸網中所處的位置不同，這種傳遞效應也不一樣，因而引起的周邊整體吊弦抬升和吊弦力的變化有所不同，并且這種差別對整體吊弦壽命的影響不可忽略。

吊弦靜態拉力以及受電弓經過1個周期內整體吊弦最大拉力的計算結果見表5。由表5可以看出，受電弓經過的1個周期內，跨內除受電弓經過的整體吊弦外，其他整體吊弦長時間保持受拉狀態。綜合考慮靜態吊弦力、受電弓經過時最大吊弦力以及對周邊整體吊弦受力影響，同一跨距內1#和5#整體吊弦的拉力(應力)水平較大，會加速整體吊弦的破壞。

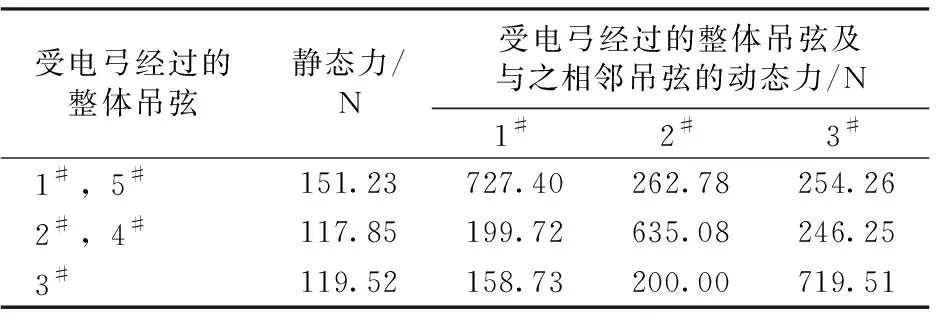
表5 受電弓經過1個周期內整體吊弦受力

受電弓經過1個周期內整體吊弦最大壓縮幅值與壓縮次數的關系見表6。由表6可以看出：同一跨距內1#和5#整體吊弦的壓縮幅值最大，3#整體吊弦的受壓縮次數最多，壓縮幅值與壓縮次數直接關系到整體吊弦的疲勞壽命，故跨內1#和5#及3#整體吊弦較為容易破壞。

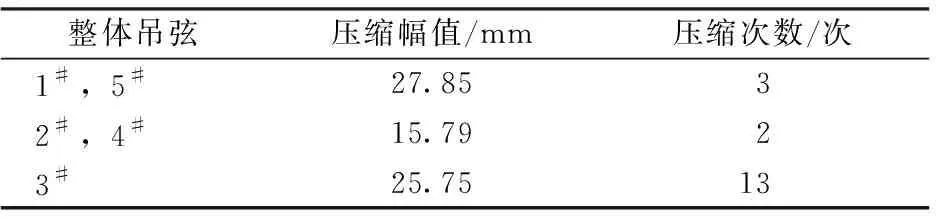
表6 受電弓經過1個周期吊弦壓縮幅值

5 結 論

(1)受電弓經過整體吊弦時，該整體吊弦的吊弦力波動相對較大，約是其靜態力的6倍。振動通過承力索、接觸線向周邊傳播，引起周邊整體吊弦力以及力的波動均明顯減小，且周邊整體吊弦始終保持受拉狀態。

(2)在同一跨內，1#和5#整體吊弦受力較大，3#整體吊弦壓縮次數最多，但3#整體吊弦位于跨中位置，接觸網彈性較大，整體吊弦的工作環境較好，不易首先發生疲勞破壞；1#和5#整體吊弦位于接觸網應力集中區域，受電弓通過時其壓縮幅值及整體吊弦力最大，工作環境最惡劣，故同一跨內1#和5#整體吊弦易首先發生疲勞破壞。

[1] 劉文濤. 電氣化鐵路接觸網的安全性探究[J]. 工程技術，2016(3): 203.

(LIU Wentao. Safety Study of Catenary System in Electrical Railway[J].Engineering Technology，2016(3): 203. in Chinese)

[2] 王偉, 吳積欽, 關金發, 等. 高速鐵路接觸網吊弦疲勞試驗臺[J]. 高速鐵路技術，2014，5(3): 22-25.

(WANG Wei，WU Jiqin，GUANG Jinfa，et al. A Fatigue Test Rig of High-Speed Railway Catenary Dropper[J]. High Speed Railway Technology，2014，5(3): 22-25. in Chinese)

[3] 楊廣英, 陳立明, 邢彤, 等. 高速鐵路接觸網振動的初步研究[J]. 鐵道技術監督，2013，41(12): 28-30.

(YANG Guangying，CHEN Liming，XING Tong，et al. Preliminary Study of Vibration Catenary System in Electrical Railway[J]. Railway Quality Control，2013，41(12): 28-30. in Chinese)

[4] 劉怡, 張衛華, 黃標. 高速鐵路接觸網動力學響應實驗及仿真[J]. 中國鐵道科學, 2005，26(2): 106-109.

(LIU Yi，ZHANG Weihua，HUANG Biao. Experiment and Simulation on Dynamic Response of the Catenary in High-Speed Railway[J]. China Railway Science，2005，26(2): 106-109. in Chinese)

[5] WU T X, BRENNAN M J. Basic Analytical Study of Pantograph-Catenary System Dynamics [J]. Vehicle System Dynamics, 1998, 30(6): 443-456.

[6] 方巖, 高仕斌. 高速接觸網整體吊弦預配[J]. 西南交通大學學報，2010，45(5): 763-767.

(FANG Yan，GAO Shibin. Integral Dropper Assembly for Overhead Contact Line of High-Speed Railway[J]. Journal of Southwest Jiaotong University，2010，45(5): 763-767. in Chinese)

[7] 周寧, 李瑞平, 張衛華. 基于負弛度法的接觸網建模與仿真[J]. 交通運輸工程學報，2009，9(4): 28-32.

(ZHOU Ning，LI Ruiping，ZHANG Weihua. Modeling and Simulation of Catenary Based on Negative Sag Method[J]. Journal of Traffic and Transportation Engineering，2009，9(4): 28-32. in Chinese)

[8] PARK T J, HAN C S, JANG J H. Dynamic Sensitivity Analysis for the Pantograph of a High-Speed Rail Vehicle [J]. Journal of Sound and Vibration, 2003, 266(2): 235-260.

[9] METRIKINE A V, BOSCH A L. Dynamic Response of a Two-Level Catenary to a Moving Load [J]. Journal of Sound and Vibration, 2006, 292(3): 676-693.

[10] ZHOU Ning, ZHANG Weihua. Investigation on Dynamic Performance and Parameter Optimization Design of Pantograph and Catenary System[J]. Finite Elements in Analysis and Design, 2011, 47(3): 288-295.

[11] CHO Y H. Numerical Simulation of the Dynamic Responses of Railway Overhead Contact Lines to a Moving Pantograph, Considering a Nonlinear Dropper[J]. Journal of Sound and Vibration, 2008, 315(3): 433-454.

[12] LEE K, CHO Y H, PARK Y, et al. A Study on Assessment of Dropper Life for Conventional Line Speed-Up [C]//The 9th World Congress on Railway Research.Lille：WCRR, 2011.

[13] 王偉. 高鐵接觸網吊弦疲勞特性研究[D]. 成都：西南交通大學, 2014.

(WANG Wei. Fatigue Characteristics Analysis of Catenary Droppers in High-Speed Railway[D]. Chengdu：Southwest Jiaotong University，2014. in Chinese)

[14] 梅桂明, 張衛華. 受電弓/接觸網系統動力學模型及特性[J]. 交通運輸工程學報，2002，2(1): 20-25.

(MEI Guiming，ZHANG Weihua. Dynamics Model and Behavior of Pantograph/Catenary System[J]. Journal of Traffic and Transportation Engineering，2002，2(1): 20-25. in Chinese)