固體氧化物燃料電池建模及廣義預測控制

李 肖，李俊紅，沈文兵，宗天成

(南通大學電氣工程學院，江蘇 南通 226019)

為使固體氧化物燃料電池(SOFC)可靠、穩定和高效地工作，需要確定系統的動態輸入-輸出特性[1]。譚勛瓊等[2]基于內部氣體流量的動態守恒方程，推導在假設條件下各種氣體分壓和電流的函數關系，進而構建SOFC的集總模型。闕加雄等[3]基于SOFC內部的3種動力學過程，綜合考慮內部的質量平衡、能量平衡和電化學反應過程，建立動態模型。SOFC的內部反應復雜，且模型具有隨機干擾、非線性等特點，因此建立的模型都很復雜，難以用于控制系統的分析和設計[4]。系統辨識方法是利用系統的輸入-輸出數據來確定系統的數學模型，更適用于工程應用[5]。

廣義預測控制算法采用反饋校正和滾動優化策略，具有較強的魯棒性，適用于復雜的工業過程控制[6]。本文作者通過SIMULINK搭建燃料電池的機理模型，分析并獲得模型的輸入-輸出數據，再辨識SOFC的數學模型，避開電池的復雜反應過程來建模，并進行廣義預測控制算法的設計。

1 SOFC機理建模

燃料電池模型電壓包括4種電壓：開環電壓(En)、活化極化損失電壓(Ua)、濃度損失電壓(Uc)和歐姆損耗電壓(Uo)。SOFC工作電壓(Ud)按式(1)計算：

Ud=En-Ua-Uc-Uo

(1)

本文作者使用MATLAB/SIMULINK軟件實現SOFC機理模型的實現，設計的基于SIMULINK的SOFC模型見圖1。

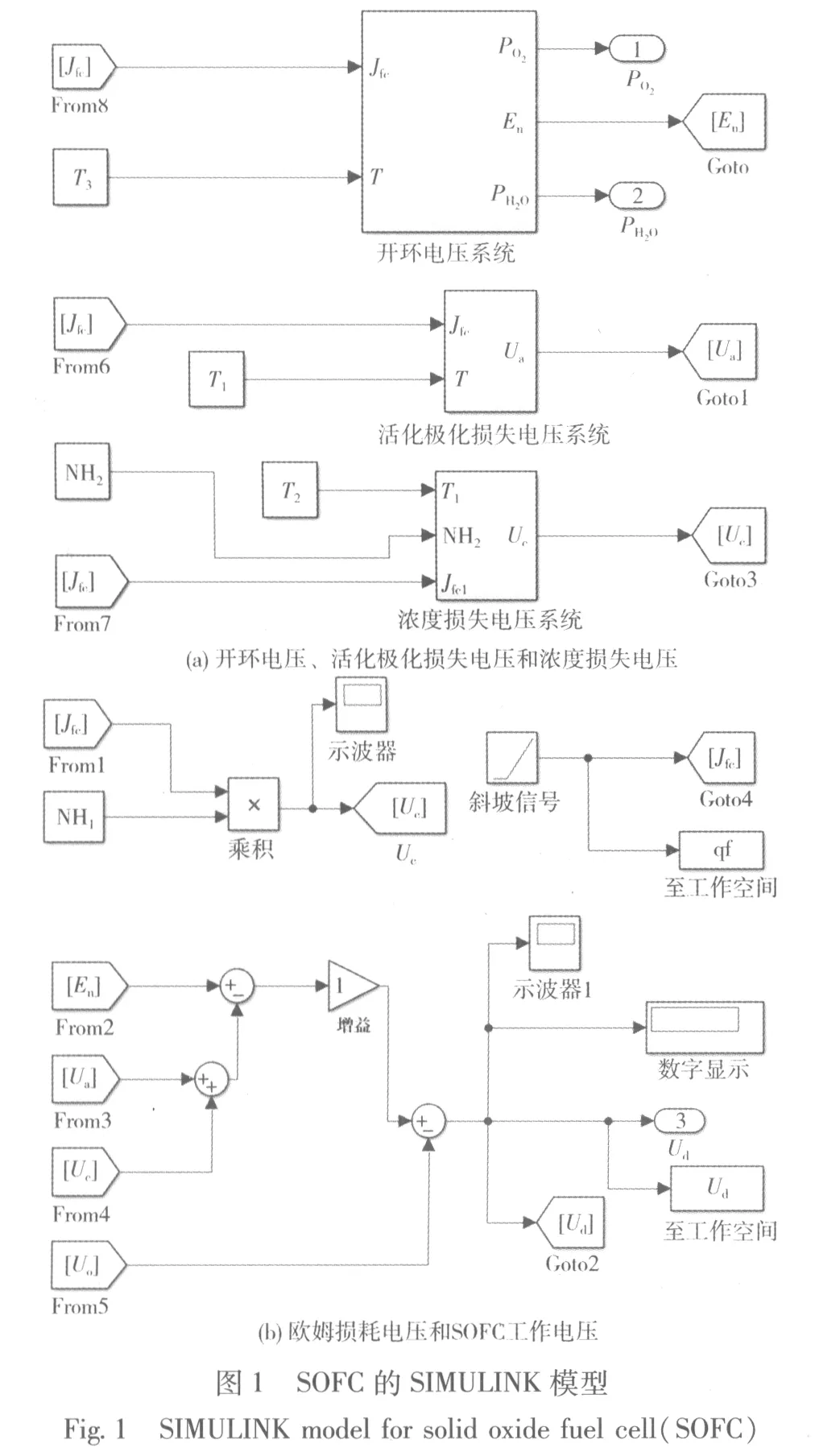
圖1中：Goto模塊用于保存端口的輸出；From模塊用于將保存的端口輸出送入指定模塊；Jfc是電流密度；qf是獲取的電流數據；T、T1、T2和T3均是工作溫度，取值為973 K；NH1是內阻，取值為0.126 Ω；NH2是輸入流速，取值為51 ml/s。

2 SOFC電池的模型辨識

系統辨識是根據動態系統的輸入-輸出數據構造數學模型的過程[5]。在理論建模太復雜的時候，經常采用系統辨識的方法。為滿足控制系統設計的需要，利用MATLAB中的系統辨識工具箱，辨識SOFC的輸出電壓響應模型，從而可避開SOFC內部復雜的反應機理。

將系統的輸入-輸出數據導入系統辨識工具箱，經過對各種模型結構辨識結果的分析與對比，最終選擇具有外部輸入的自回歸滑動平均(ARMAX)模型作為SOFC的模型結構。通過系統辨識工具箱辨識出的系統具體參數為：

A(q-1)=1-1.22q-1+0.22q-2

(2)

B(q-1)=0.99

(3)

C(q-1)=1+0.927q-1

(4)

式(2)-(4)中：q-1為時延因子；A(q-1)、B(q-1)和C(q-1)均是q-1的多項式，為系統參數。

3 SOFC的控制設計

3.1 廣義預測控制算法簡介

廣義預測控制(GPC)算法結合了多種算法的優點[6]，如果能加以應用，可提高SOFC系統的控制效果。

3.2 預測模型

GPC采用式(5)作為系統的預測模型

A(q-1)y(k)=B(q-1)u(k)+C(q-1)ξ(k)/δ

(5)

式(5)中：δ為差分算子，δ=1-q-1；k表示采樣時刻序列；y(k)、u(k)是系統的輸出、輸入；ξ(k)是均值為零的白噪聲序列。

為了進行柔化控制，控制的目標是跟蹤如式(6)所示的參考軌線。

w(k+j)=ajy(k)+(1-aj)yr(j=1，2，…，n)

(6)

式(6)中：j為預測長度；w(k+j)為系統的超前j步參考軌線；y(k)和yr分別為輸出值和設定值；α為柔化系數，0<α<1。

根據預測控制理論，引入Diophantine方程可得到：

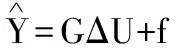
(7)

(8)

(9)

ΔU=[Δu(k)，Δu(k+1)，…，Δu(k+n-1)]T

(10)

f=[f(k+1)，f(k+2)，…，f(k+n)]T

(11)

3.3 最優控制律

若令W=[w(k+1),w(k+2)，…，w(k+n)]T，則目標函數J可寫成：

J=(Y-W)T(Y-W)+λΔUTΔU

(12)

式(12)中：Y是輸出矩陣。

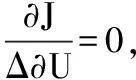
ΔU=(GTG+λI)-1GT(W-f)

(13)

如式(13)所示，在控制量加權系數λ和柔化后的設定值向量W均已知的情況下，若求ΔU必須先知道G和f。由式(7)可得：

y(k+n)=gn-1Δu(k)+…+g0Δu(k+n-1)

+f(k+n)+Enξ(k+n)

(14)

令X(k)=[Δu(k)，Δu(k+1)，…，Δu(k+n-1)，1]，θ(k)=[gn-1,gn-2,…,g0,f(k+n)]T，輸出預測值可寫成：

y(k+n/k)=X(k)θ(k)

(15)

式(15)中：X(k)為信息向量；θ(k)為待估計參數向量。

θ(k)可用最小二乘法估計得到：

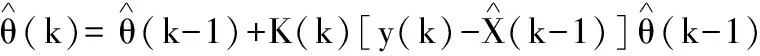
(16)

(17)

(18)

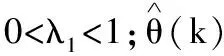
預測向量f可由式(19)得出：

(19)

在求得G和f后，可計算控制量ΔU的值，從而計算預測輸出值。

3.4 比例積分微分控制算法

比例積分微分(PID)控制器是發展最早的控制方法之一，涉及的算法設計和結構都很簡單，且適用于工程應用。目前，PID控制憑借簡單易懂、適應性強等優勢，仍然在實際生產中獲得廣泛應用。PID控制器根據給定值與實際輸出值構成控制偏差e(t)，偏差e(t)與控制量u(t)的關系為：

(20)

式(20)中：Kp為比例系數；Ti為積分時間常數；Td為微分時間常數。

3.5 仿真研究與分析

在對SOFC建模時，選擇ARMAX模型為最終辨識結果，參數可由系統辨識工具箱獲得。ARMAX模型的形式為：

A(q-1)y(t)=B(q-1)u(t)+C(q-1)e(t)

(21)

將式(2)、(3)和(4)辨識出的參數A(q-1)、B(q-1)和C(q-1)代入ARMAX模型的一般形式，整理得到：

y(t)=1.22y(t-1)-0.22y(t-2)+0.99u(t)

+e(t)+0.927e(t-1)

(22)

辨識出的模型采用廣義預測控制算法，通過控制氧氣的流量，研究在外部負載(電流)突然增大或減小時，電池輸出電壓的跟蹤性能。選取設計參數：模型長度p=6，預測時域長度n=6，控制時域長度m=2，控制加權系數λ=0.7，柔化系數α=0.5；最小二乘法參數初始值為：gn-1=1，f(k+n)=1，其余為0，廣義預測控制效果如圖2(a)所示；針對SOFC模型，設計PID控制器，控制效果見圖2(b)。

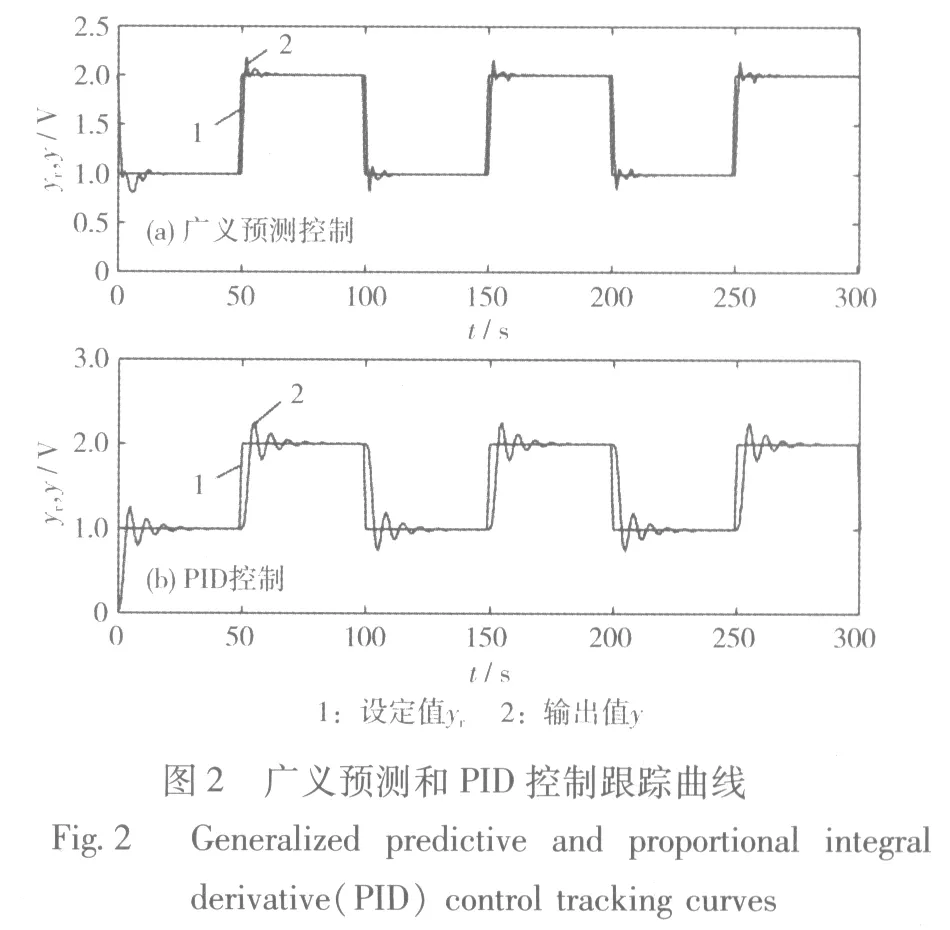
從圖2可知，當系統的設定值發生變化時，兩種算法經過一段時間調節之后，均能達到穩定值，但廣義預測控制算法的調節時間更短，大約為12 s，最大超調量大約為7%，而在PID控制算法下，輸出曲線經過約31 s達到穩定值，最大超調量大約為11%，因此廣義預測控制算法跟蹤給定值的控制效果較好，超調量更小，系統的響應速度更快。與PID控制相比，廣義預測控制算法具有更好的跟蹤性能。

4 總結

本文作者分析了SOFC的反應機理，建立了SOFC的物理模型，從而獲得電池模型的輸入-輸出數據。根據這些數據，再用MATLAB中的系統辨識工具箱辨識SOFC的ARMAX模型。利用系統辨識避開了電池內部復雜的反應機理，使用價值很高。根據辨識得到的ARMAX模型設計廣義預測控制算法，并與經典的PID控制對比。結果表明：當電池的負載發生擾動時，廣義預測控制算法具有更好的跟蹤效果。