大氣能見度對光偏振特性的影響*

劉 成， 高 雋， 范之國

0 引 言

大氣光散射具有的特定偏振信息是遙感探測手段的重要理論基礎[1～3]。散射光的偏振信息能夠提供更多的目標信息，提高對目標的探測能力[4]。大氣層粒子光散射最直觀的表現形式為大氣能見度對天空偏振特性的影響[5]，因此，了解大氣能見度變化影響下的光偏振特性對深入研究大氣偏振以及大氣偏振探測技術的進一步發展均具有重要意義。

墨西哥的Lara E R[6]利用氦—氖(He-Ne)激光研究了穿過不同濃度霧后的Henyey-Greenstein相函數和消光系數等的變化情況，結果表明隨著霧濃度的增加對光偏振信息具有很大程度上的消偏。徐敬一等人[7]利用蒙特—卡羅方法仿真了不同粒子濃度下的光偏振特性。姜會林、張肅等人[8]利用激光定性開展了煙霧濃度對偏振信息影響的實測實驗，引起了對光偏振信息影響機理的深入討論，對大氣光偏振信息研究具有十分重要的意義。劉建斌[9]利用黎卡地—貝塞爾函數模擬了不同粒子尺度的散射光強和偏振特性。當粒子尺度增加時，散射光強增加，水平偏振變得不對稱，而垂直偏振沒有變化；當粒子的折射率虛部增加時，散射光強減少，偏振信息也發生相應的變化。張肅、彭杰和孫賢明等人[10]均從粒子形態和復折射率方面對光偏振特性展開了研究。上述研究對進一步研究大氣偏振特性具有十分重要的參考價值。但實際環境中介質粒子的濃度難以測得，粒子形態各異，難以完成對偏振信息變化的定量化研究。

本文提出了一種大氣能見度影響下的大氣光偏振特性研究方法。通過建立能見度與光學厚度之間的數學模型，基于偏振蒙特-卡羅方法仿真了不同大氣能見度下的光偏振特性，并在偏振光學模擬實驗艙中模擬不同大氣能見度環境，進行了實測研究，探索不同大氣能見度情況下對光偏振特性的影響。

1 大氣能見度與傳輸介質參數的數學模型

假設大氣均勻，即大氣消光系數為恒定值，得到大氣能見度的Koschmieder定律公式[11，12]

(1)

式中V為能見度；ue為消光系數；T′為對比視覺閾值，通常T′=0.05。當取0.05時，式(1)為

(2)

從式(2)可以看出，V和1/ue成正比。

假設散射粒子為均勻球型粒子，介質厚度為L，介質中的粒子濃度為ρ，粒子半徑為r，當光穿越介質時，如圖1所示，滿足Beer-Lambert定律

I=I0e-ueL

(3)

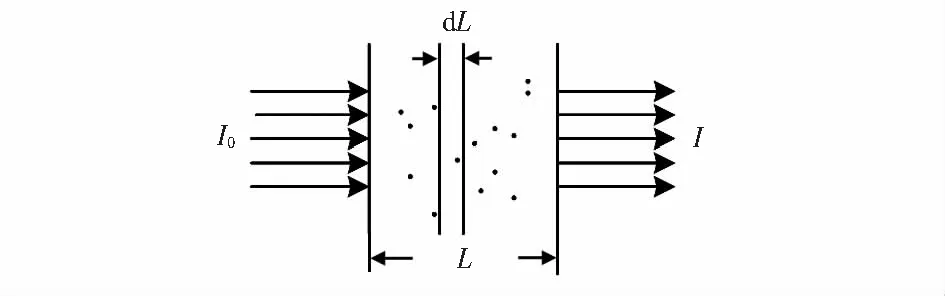
圖1 光束穿越介質示意

根據Mie散射理論，散射截面積A為

A=πr2

(4)

代入到散射系數us和吸收系數ua的計算公式得

us=ρAQsca(m,r,λ)=ρπr2Qsca(m,r,λ)

(5)

us=ρAQabs(m,r,λ)=ρπr2Qabs(m,r,λ)

(6)

式中Qsca(m,r,λ)+Qabs(m,r,λ)=Qe(m,r,λ)為消光效率因子，為折射率m、粒子半徑r和波長λ的函數；ρ為粒子濃度。

根據消光系數的定義，消光系數ue為

ue=ua+us=ρπr2(Qabs(m,r,λ)+Qsca(m,r,λ))

(7)

將式(7)代入式(2)中可得

(8)

由式(8)可知，大氣能見度和粒子濃度的倒數1/ρ成正比，將能見度對粒子濃度的影響代入偏振蒙特—卡羅傳輸的仿真程序中，即可仿真出大氣能見度對光偏振特性的影響。

式(8)中，消光效率因子[13]Qe(m,r,λ)為

(9)

式中an和bn為Mie散射系數，僅與散射介質的復折射率m和尺度參數x=2πr/λ有關。

實際實驗環境中使用的濃度一般為質量濃度(g/mL)，而偏振蒙特—卡羅程序中的粒子濃度為單位體積里的粒子個數(個/mL),二者不匹配，可由式(3)和式(6)確立粒子濃度和光透過率之間的關系[8]

T=I/I0=exp(-τ)=exp(-ρπr2QeL)

(10)

式中T為光透過率；τ=ueL為光學厚度。

在同一介質中，介質厚度L保持不變，則可由光學厚度表征能見度。又因πr2QeL為常數，因此，介質濃度和光學厚度成正比。在仿真過程中，由光學厚度表征能見度，改變光學厚度τ值，便可實現介質濃度ρ的變化；而在實測實驗中，通過測量光透過率T即可算出光學厚度τ值，進而測量不同光學厚度下的傳輸光偏振信息變化情況。因此，用光學厚度τ表征大氣能見度V的變化，可以建立理論和實驗之間的聯系，從而驗證大氣能見度對偏振特性的影響。

2 仿真實驗與分析

以標準蒙特—卡羅方法[13]為基礎，通過發射不同偏振態的光子，經過由偽隨機數構造的散射介質環境后，在接收靶面上統計出射光子的偏振信息，可實現對傳輸光穿越散射介質過程的模擬。為了模擬實際大氣環境介質，在偏振蒙特—卡羅仿真程序中，設置傳輸光波長為600 nm，介質粒子半徑為1 μm，復折射率為1.6+0.01i，光子總數為106個。

2.1 光學厚度對偏振信息分布的影響

圖2 不同光學厚度下水平線偏振光散射后DOP和θ分布

2.2 光學厚度對偏振度均值的影響

在蒙特—卡羅仿真實驗中，選用光學厚度在0～4之間進行實驗，每間隔0.2進行一次仿真，統計在不同光學厚度下，上述5種偏振光偏振度均值的變化情況。

實驗結果如圖3所示，可以看出:隨著光學厚度的不斷增加，偏振光的偏振度出現了消偏，并且當τ≤0.2時，偏振度下降幅度很大；當0.2<τ≤3時，偏振度下降的幅度逐步變緩；當τ>3以后，偏振度幾乎不變化，偏振度達到飽和狀態。這是因為隨著光學厚度的增加，散射介質的能見度降低，粒子散射增強，改變了原來的偏振特性，導致偏振度整體趨勢逐步降低，但當光學厚度τ>3后，介質粒子散射達到飽和，偏振度幾乎不發生變化。

圖3 偏振度均值隨光學厚度變化仿真曲線

3 實測實驗與分析

為了驗證上述偏振蒙特—卡羅仿真實驗結果的正確性，需要在偏振光學模擬實驗艙內模擬大氣霧天環境進行相應的實測實驗。由光學厚度τ表征大氣能見度V的變化。實驗中采用能見度儀可同時測量出某一時刻的能見度值和光透過率值，而光透過率和光學厚度之間的關系為

T=I/I0=e-τ

(11)

利用上述關系在偏振光學模擬實驗艙內測量出10組不同時刻的能見度V和T光透過率數據如表1所示，并換算得出了該時刻的光學厚度值τ。

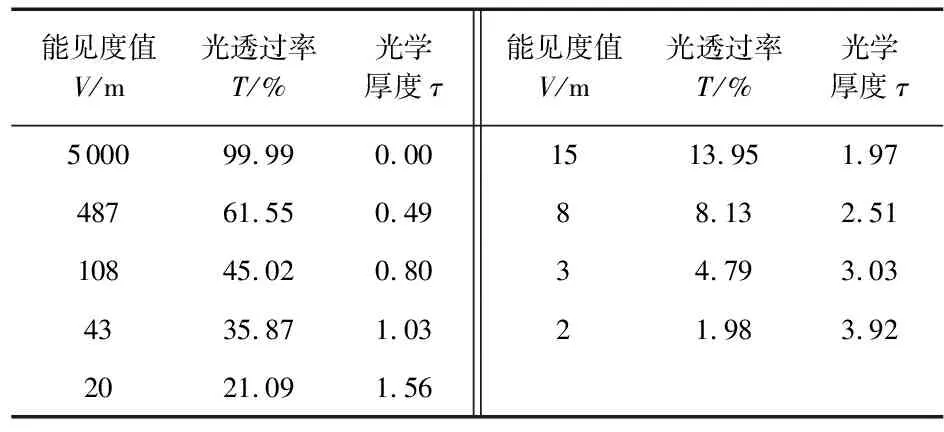
表1 光透過率與光學厚度之間的關系

偏振光學模擬實驗系統框圖如圖4所示，積分球能夠產生光強均勻的可見光光源，色溫為3 000 K，在其前端加偏振片即可調制出偏振光。偏振光學模擬實驗艙周圍配備有溫濕度傳感器和能見度儀等多種傳感器可實現對實驗艙內環境的定量化模擬，通過煙霧發生器或者水霧發生器向實驗艙內添加煙或水霧成分，可達到定量模擬大氣霧天環境的效果。3電荷耦合器件(charge coupled device,CCD)同時成像偏振相機作為接收設備，該相機有3個通道可以同時拍攝出0°,60°和120° 3幅偏振角度下的偏振圖像，用于求解出偏振分布的4個斯托克斯矢量，計算公式為

(12)

圖4 偏振光學模擬實驗系統框圖

在實測實驗中，以入射水平線偏振光[1100]為例，通過3CCD同時成像偏振相機采集某一時刻下經偏振光學模擬實驗艙傳輸的3幅0°，60°和120°偏振角度下的偏振光強圖像，并恢復出斯托克斯3個分量I，Q，U，利用式(13)可計算出偏振度和偏振角

(13)

圖5為不同光學厚度下入射水平線偏振光時偏振度圖案，可以看出：當光學厚度τ≤1.03時，由于偏振相機感光CCD過曝光，偏振度圖像中心會出現黑色光斑，對實驗結果造成一定影響。隨著光學厚度的不斷增加，偏振度圖案逐步退化變暗，這是由于粒子濃度增大、散射次數增多，粒子間的散射作用導致消偏現象引起。

圖5 不同光學厚度下入射水平線偏振光的DOP分布

為了進一步從數值上說明能見度變化對偏振度信息的影響，統計了入射水平線偏振光時，偏振度均值的變化情況，如圖6(a)所示，隨著光學厚度的不斷增加，水平線偏振光偏振度均值不斷下降，并且在開始階段偏振度下降的幅度較大，隨著光學厚度的進一步增加，下降趨勢減緩，這是由于粒子散射次數達到接近飽和狀態時，消偏作用達到最大，偏振度幾乎降為最小值。在τ=1.5左右時，偏振度變化趨勢有所波動，這是由于此時中心光斑過曝光導致偏振度圖案中心變黑所致。由大氣能見度的數學建模可知，能見度和光學厚度成反比關系，圖6(b)為隨著能見度的增加，偏振度的變化趨勢，不難看出:其變化趨勢與圖6(a)恰好相反。在進行實測實驗時，由于存在煙霧瞬時變化不可控性、煙霧粒子半徑不均勻且較小等原因，導致實測偏振度和仿真偏振度存在一定差異。但偏振度均值的整體變化趨勢和仿真實驗結果相一致。

圖6 水平線偏振光偏振度均值的變化趨勢

4 結 論

針對大氣能見度對光偏振特性的影響問題，用光學厚度表征能見度，分別利用偏振蒙特卡羅方法仿真了整個傳輸過程以及利用偏振光學模擬實驗艙進行了相應的實測實驗。通過仿真與實測數據2方面的對比，說明了大氣能見度對光偏振特性的影響，從而驗證了結果的正確性。

參考文獻:

[1] 宋茂新,孫 斌,孫曉兵,等.航空多角度偏振輻射計的偏振定標[J].光學精密工程,2012,20(6):1153-1158.

[2] 趙開春,盧 皓,尤 政.天空光偏振模式自動探測裝置[J].光學精密工程,2013,21(2):239-245.

[3] 黃旭鋒,步 揚,王向朝.基于米氏散射理論的太陽光散射偏振特性[J].中國激光,2010,37(12):3002-3006.

[4] 孔凡輝，陳青山，劉 洋，等.多發光目標的高速跟蹤[J].傳感器與微系統，2017，36(5)：33-35.

[5] 唐慧強，張 耀.散射式能見度儀設計[J].傳感器與微系統，2016,35(1)：121-123.

[7] 徐敬一,高 雋,張陽陽,等.光在不同濃度介質中散射傳輸的偏振特性分析[J].電子學報,2015,43(8):1604-1609.

[8] 張 肅,戰俊彤,白思克,等.煙霧濃度對偏振光傳輸特性的影響[J].光學學報,2016(7):303-310.

[9] 劉建斌,吳 健.球形粒子的散射和偏振特性研究[J].激光技術,2005,29(1):66-67.

[10] 孫賢明,王海華,申 晉,等.隨機取向雙層橢球粒子偏振散射特性研究[J].物理學報,2011,60(11):370-376.

[11] 傅 剛,李曉嵐,魏 娜.大氣能見度研究[J].中國海洋大學學報:自然科學版,2009,39(5):855-862.

[12] 許 茜,殷緒成,李 巖,等.基于圖像理解的能見度測量方法[J].模式識別與人工智能,2013,26(6):543-551.

[13] 陶宗明,張寅超,張改霞,等.氣溶膠粒子消光效率因子的特性研究及尺度譜的擬合[J].量子電子學報,2004,21(1):103-109.

[14] 鄭驪昂，高 雋，于 洋，等.大氣介質環境后散射穆勒矩陣的特性分析[J].傳感器與微系統，2017,36(5)：22-24.