風力載荷對實船參數橫搖預報的影響研究

周耀華 ，馬 寧 ， 尹曉輝 ， 魯 江 ，石 珣

（1.中國船級社上海規范研究所，上海 200135；2.上海交通大學海洋工程國家重點實驗室，上海 200240；3.中國船舶及海洋工程設計研究院，上海 200011；4.噴水推進技術重點實驗室，上海 200011；5.中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

自APL CHINA號在北太平洋遭遇了嚴重的參數橫搖事故[1]以來，集裝箱船的參數橫搖現象引起了海事界的高度關注。由于該現象能夠引起船舶的大幅橫搖，故而作為一種嚴重危害船舶安全的重要穩性失效模式，已被國際海事組織（IMO）納入了研究范圍，并取得了部分研究成果[2-7]。

船舶的實際航行經驗表明，即便迎浪航行，也有可能長時間承受斜風載荷的作用。由于前人的研究多側重于迎浪或隨浪航行時的參數橫搖響應，因此風力載荷的影響多被忽略。近年來，風浪聯合作用的水動力學問題逐漸引起了一些學者的關注。Bulian[8]對于風浪聯合作用下的橫搖運動預報開展了工作，考慮了平均風速和陣風的作用，風力譜基于Davenport譜。Chang[9]在參數橫搖的研究中，對頂浪、隨浪和斜浪的情況均進行了計算，其運動模型基于Blendermann的方法，對橫搖自由度考慮了風力載荷的作用，并取得了有意義的成果。本文在前人的基礎上，通過對3艘集裝箱船和1艘散貨船在規則波作用下的參數橫搖敏感性計算，基于弱非線模型研究了風力載荷假定對實船參數橫搖預報結果的影響。

1 風浪聯合作用的數值模型

1.1 風載荷假定

大型集裝箱船由于甲板上裝載集裝箱，水線以上側投影面積與風傾力臂之積通常較大，因此惡劣氣象條件下承受的風傾力矩將會十分可觀。在CMV CCNI GUAYAS事故[7]期間，風向和浪向在較長時間內存在明顯差異。這表明在實際海況下，即使船舶迎浪航行也有可能會承受風載荷引起的橫搖力矩。

本文的研究假定船舶迎浪航行時遭遇側風，此時船舶受到側風橫向分量引起的橫傾力矩激勵。風力載荷假定為隨時間改變的風傾力矩。根據風的類型、平均風速、地理區域和地形等多種因素，風力譜可假定為多種型式[8]，本文對時變風速的計算采用Davenport譜：

其中為平均風速和時歷風速變化項；AL為船側面受風面積；Hc為風傾力臂，取從側受風面積中心至平均吃水1/2處的垂直距離；Cm為空氣阻力系數。

現代集裝箱船出于營運需求對于航線和時間安排十分緊湊，遭遇惡劣海況的概率較高。本文中平均風速Uw參照2008年國際完整穩性規則（2008 ISCode）假定為26 m/s。平均風速的取值是IMO根據166個海難報告的氣象條件統計后選取的，參與統計的絕大多數海難發生于蒲氏風級4至10級的惡劣海況下。對于空氣阻力系數Cm，可以采用風洞試驗測量。本文參照2008 ISCode對于若干實船風洞試驗結果綜合后的取值，假定為1.22。該系數已經考慮了風傾力臂定義的影響。

1.2 風浪聯合作用的參數橫搖數值模型

對于參數橫搖的預報，勢流理論以及非線性力學的方法得到了廣泛應用。國際上主要有歐盟資助的SAFEDOR項目和ITTC波浪中穩性委員會主導的研究項目以及日本學者Umeda等人[11]的研究工作，并取得了豐碩的成果[12-14]。國內的楊素軍，范余明[15]，付麗坤，蔣志鵬[16]，常永全，范菊[17]，唐友剛，鄺艷香，李紅霞[18]，魯江[19]，陳京普[20]等學者也開展了深入的研究。

本文采用的運動預報模型基于典型的弱非線性三自由度模型[2]。此類考慮時延效應和F-K力非線性的弱非線性方法已在對參數橫搖的研究中得到過成功應用[11，17]。運動方程見下式：

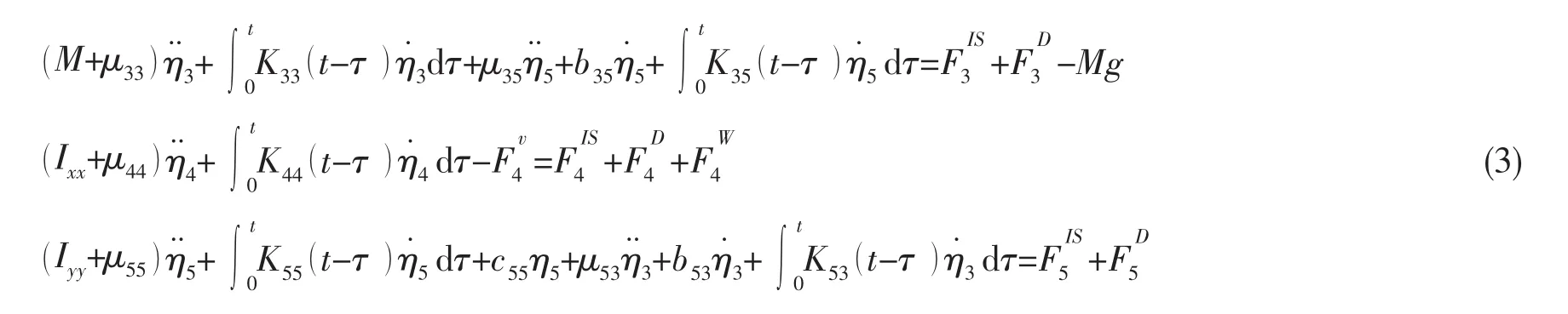
式中為根據1.1節中假定簡化后的側風橫向分量引起的時變橫傾力矩（見（1）式）。假定航速在風阻和波浪增阻綜合作用下趨于穩定，僅考慮垂蕩、橫搖和縱搖的耦合運動。F-K力和回復力的合力的計算基于三維壓力積分方法，且考慮了由于船體瞬時濕表面積所引起的非線性效應。輻射力和繞射力FD的計算基于三維頻域線性水動力方法。其中輻射力的計算基于脈沖響應函數理論，以考慮時延效應：

式中：）為頻域理論計算的興波阻尼。粘性效應簡化為橫搖粘性阻尼力矩，可采用橫搖衰減試驗結果或Ikeda方法[21]估算。μjk為通過在平均濕表面下求解三維邊值問題得到的附加質量和附加慣性矩，計算表達式及定解問題如下：

構造積分方程，采用三維方法計算。積分方程為：

其中

首先采用C11集裝箱船模型在波長船長比為1.0、不同波陡下的試驗結果[19]對本文的計算模型進行驗證計算。粘性橫搖阻尼基于試驗數據。

參數橫搖對于橫搖慣性矩和GM值具有極高的敏感性，而通過模型試驗無法高精度的測量模型慣性矩，因此為了盡量消除慣性矩對數值模型精度驗證的影響，對于C11船模橫搖慣性矩采用了如下方式計算：

首先采用近似公式，根據試驗測定的橫搖固有周期估算橫搖慣性矩。

其中：IXX為船舶橫搖慣性矩為船舶質量（kg）；g為重力加速度；GM 為初穩性高度（m）；T為橫搖固有周期（s）；附加慣性矩△IXX采用三維勢流理論計算得出。

然后以（8）式結果為初始值，采用粘流CFD求解器ISIS-CFD通過模擬船模靜水橫搖衰減計算船模橫搖固有周期。依據比較橫搖固有周期計算值與船模試驗結果的誤差，迭代確定橫搖慣性矩的取值。該方法曾成功應用于對安裝有附體的軍船模型的橫搖衰減模擬，取得了良好的結果[22]。圖1給出了采用初值迭代計算過程中，橫搖慣性矩取值對應的橫搖固有周期誤差結果。由圖1可見，初始估算值對應的固有周期誤差較大，而迭代收斂點的誤差已由初始的5.3%降至-0.1%。C11驗證計算采用慣性矩最終迭代結果。

參數橫搖現象發生時的橫搖和縱搖的時歷運動響應表明（見圖2），橫搖周期近似為縱搖周期的兩倍，即所謂的2：1響應。F-K力和恢復力的計算結果也表現出一定的非線性效應。圖3給出了不同入射波陡時數值計算結果與試驗結果的比較。

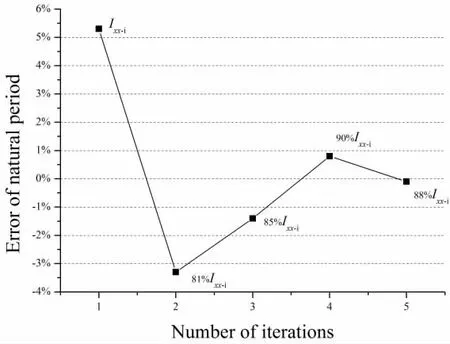
圖1 慣性矩迭代過程對應的橫搖固有周期誤差Fig.1 Error of natural roll period during iteration

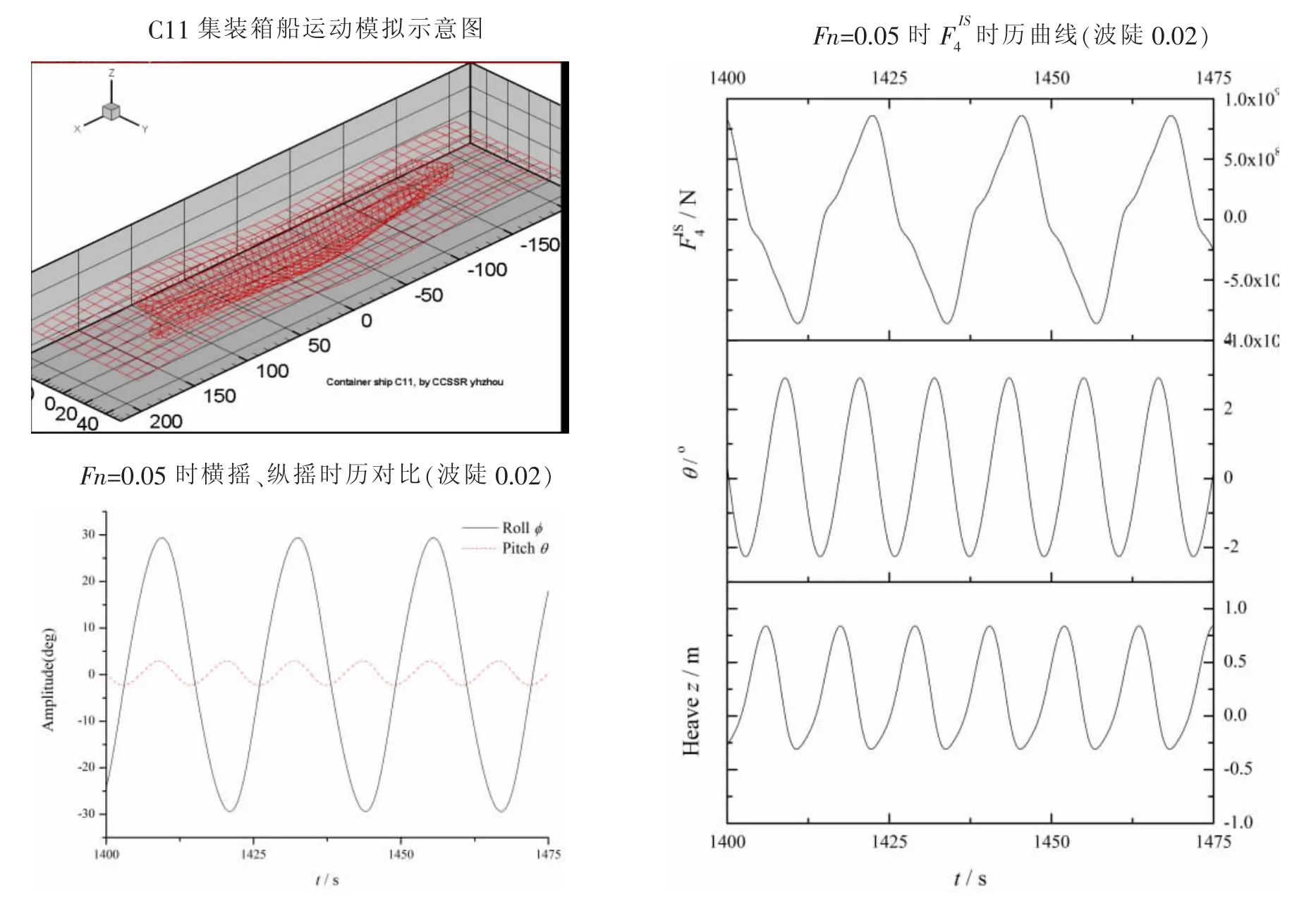
圖2 C11船模參數橫搖運動響應模擬及F-K力時歷Fig.2 Simulations of parametric roll of C11 and the time-history of F-K force

實船事故的經驗表明[1]，當船舶穩定地發生較大幅值的參數橫搖時，船舶、貨物及人員的安全受到了嚴重威脅。因此對于實船工程預報而言，能否準確預報發生大幅參數橫搖現象，特別是提高橫搖幅值安全臨界點附近的預報精度對于船舶安全性評估具有重要工程意義。目前IMO傾向于采用滿足適度精度且相對簡化的模型[23]用于工程實踐，并暫時將橫搖幅值25°作為判斷是否發生威脅船舶安全的參數橫搖現象的安全臨界點。若假定25°橫搖角作為可能威脅船舶安全的標準值判斷，則采用本文的數值模型針對C11船模的成功預報概率為91.67%，虛警率為8.33%，而預報失敗率為0.0%。因此針對C11模型個案的分析表明，本文采用的三自由度運動模擬方法在安全臨界點附近滿足適度的預報精度，能夠較為準確地對船舶動穩性安全性進行評估。由于參數橫搖的非線性特征，采用相對簡化的弱非線性模型必然在數值模擬精度上有所犧牲。該數值模型輻射、繞射力的模擬未能考慮非線性影響，橫搖粘性阻尼的計算也是基于船模靜水橫搖試驗的處理結果。此外出于簡化動力學模型考慮也沒有計入航速變化的影響，因此導致數值模型對于參數橫搖幅值的計算精度有所降低。但結合其對于C11船模能否發生大幅參數橫搖的預報效果，該模型總體上適用于實船參數橫搖安全性評估。

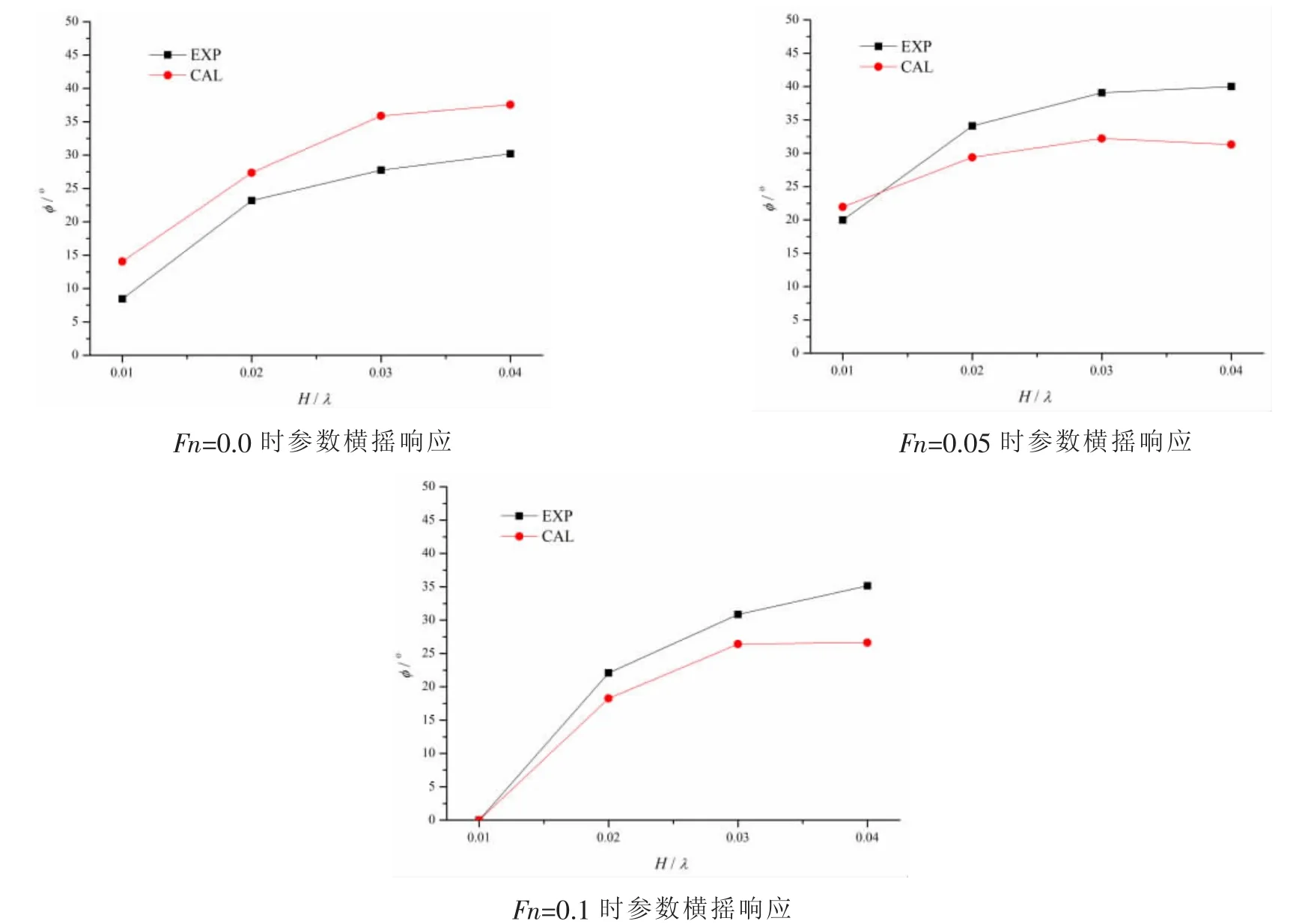
圖3 C11船模參數橫搖響應對比Fig.3 Comparison of parametric roll response of C11

2 計算結果及風載荷影響分析

參考IMO采用Level 1衡準進行實船分析的結果[3]，本文選定了3艘集裝箱船（C1～C3）和1艘散貨船（B1）總計12個經批準的裝載工況（系指實船被主管當局批準用于營運的裝載工況）進行計算，分析風載荷對于實船參數橫搖預報結果的影響。主尺度和裝載工況見表1。

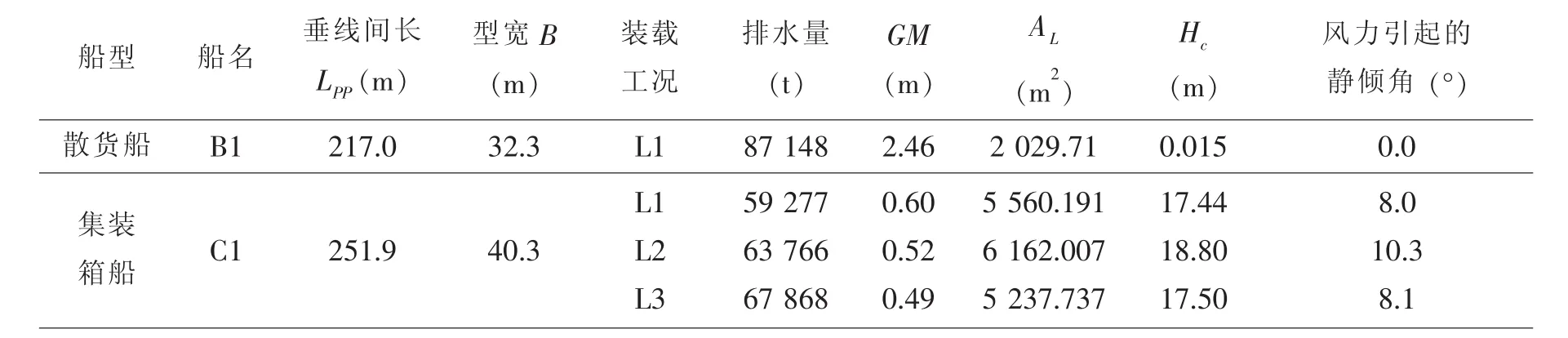
表1 實船主尺度Tab.1 Principal dimensions of full scale ships

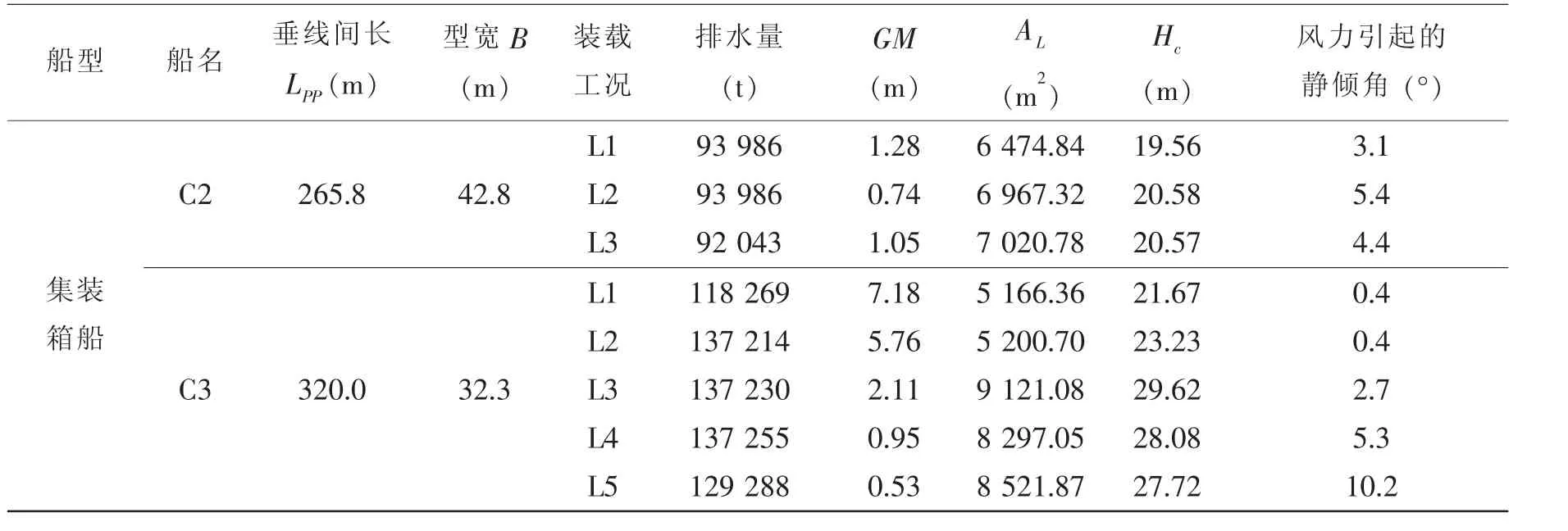
續表1

本文對于實船的粘性阻尼均采用簡化的Ikeda方法[21]進行計算。對于規則入射波條件下風力載荷影響的研究，計算航速為Fn=0.05、0.1和0.15，浪向為迎浪。入射波陡的選取與風載荷假定中關于惡劣氣象條件的假定保持一致。以C3為例，入射波波高選取波長船長比為1.0時的總計3個波陡，波高分別為3.2 m、6.4 m和9.6 m。當采用Grim的等效波理論[24]，根據IACSRec.34北大西洋統計資料計算等效入射波波高，則有義波高4.5 m對應最大等效波高為3.2 m；有義波高6.5 m對應最大等效波高為4.6 m；有義波高8.5 m對應最大等效波高為6.16 m。因此，本文計算所采用的波陡系數涵蓋了惡劣氣象條件下的相應海況。

圖4 風載對參數橫搖響應的影響Fig.4 Effect of wind load on parametric roll

圖4給出了風載對參數橫搖運動收斂速度的影響以及對臨界裝載工況誘發參數橫搖相應的對比。圖5給出了是否計入風載時，船舶受到的橫搖力矩和恢復力矩的對比結果。

在數值計算過程中，風傾力矩縮短了參數橫搖響應發展的時間，促進橫搖幅值更快趨于穩定。當裝載工況遭遇的入射波陡接近誘發參數橫搖的臨界波陡時，該裝載工況實際上處于臨界狀態，此時由于風載荷的作用從而誘發了穩定的參數橫搖運動。由此可以認為風載荷對于誘發參數橫搖起積極作用，降低了誘發參數橫搖響應的入射波幅門檻。這表明，船舶即便遭遇相對較小的海況時，也可能在風傾力矩作用下誘發參數橫搖響應。在實船預報中如果忽略風載荷的作用，有可能低估參數橫搖的發生概率。

由圖5可見，由風載荷引起的橫搖力矩相對入射波力始終為小量。風傾力矩對波浪中GZ曲線的作用較為復雜，GZ曲線的最大值相對不計風載情況有顯著提高，但峰值在不同周期也有顯著降低，甚至引起GZ出現負值。

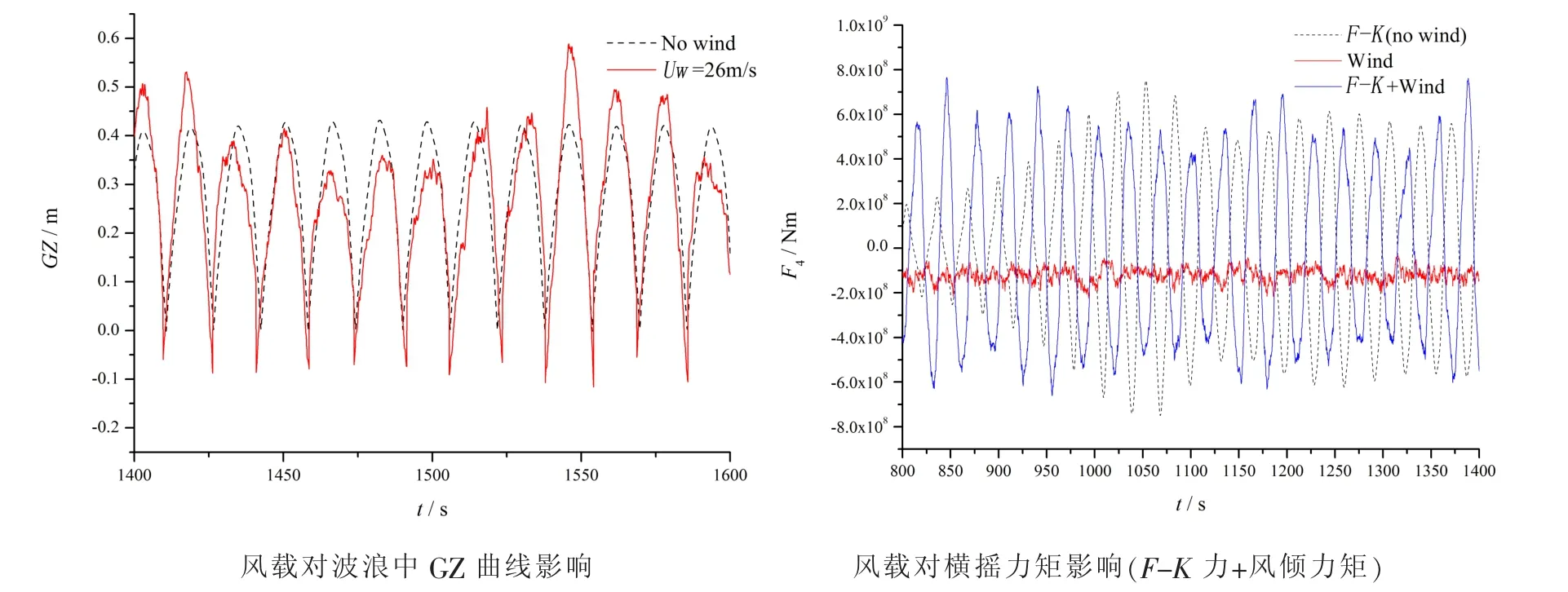
圖5 風載對于橫搖力矩的影響Fig.5 Effects of wind load on roll moment（C3-L4，Fn=0.05，λ/L=1.5，H/λ=0.01）

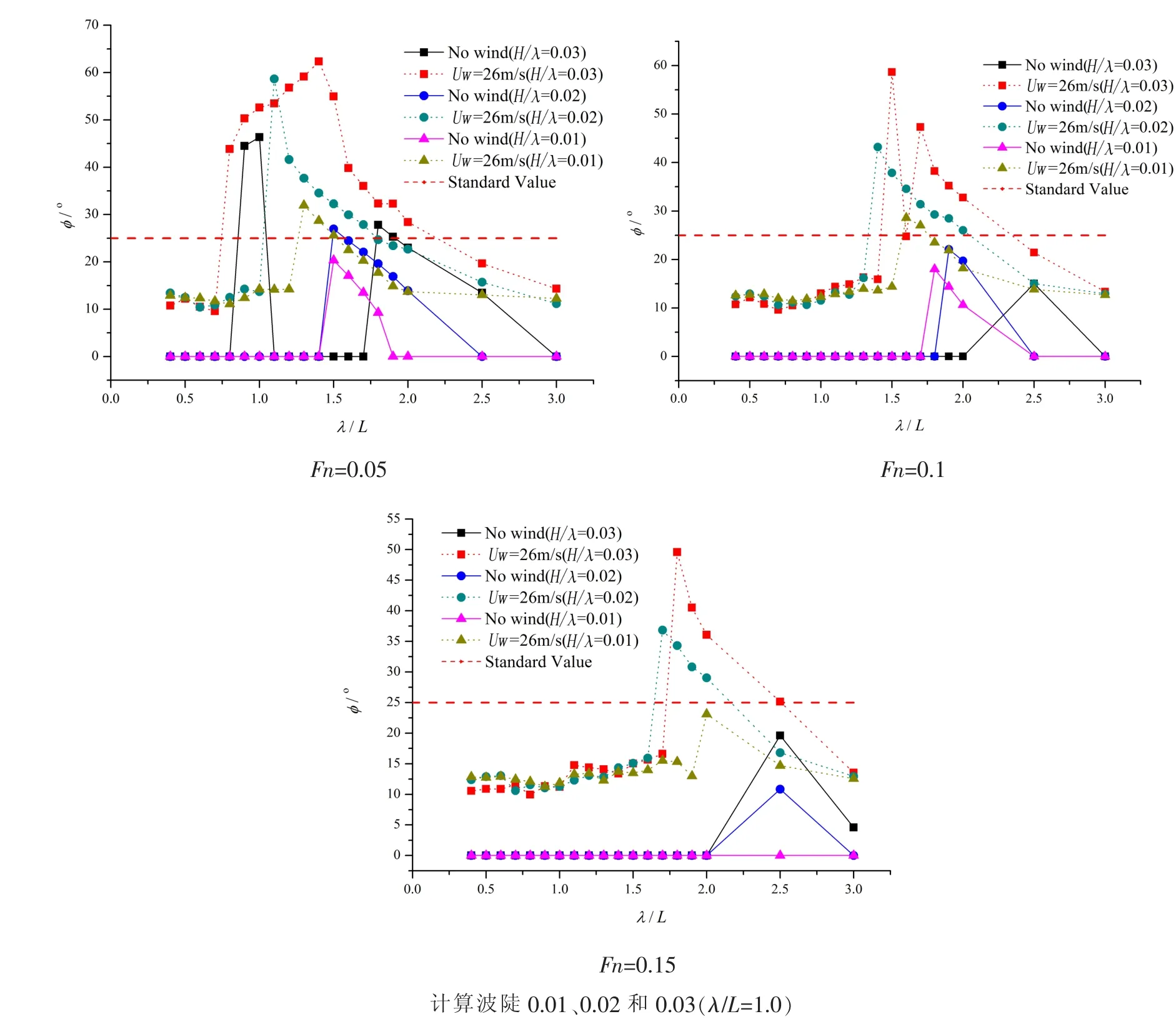
圖6 風力載荷對橫搖響應對應的入射波頻率及其幅值影響（C3-L4）Fig.6 Effects of wind load on wave frequency and roll amplitude of PR(C3-L4)

圖6給出了C3船的L4工況不同入射波波陡時，風載對參數橫搖響應頻率和幅值影響對比。計算結果表明，風傾力矩在無風情況的臨界頻率附近，誘發了參數橫搖，即擴大了發生參數橫搖的頻率范圍，并增大了參數橫搖的幅值。這也證明風載荷對于誘發參數橫搖起到促進作用。

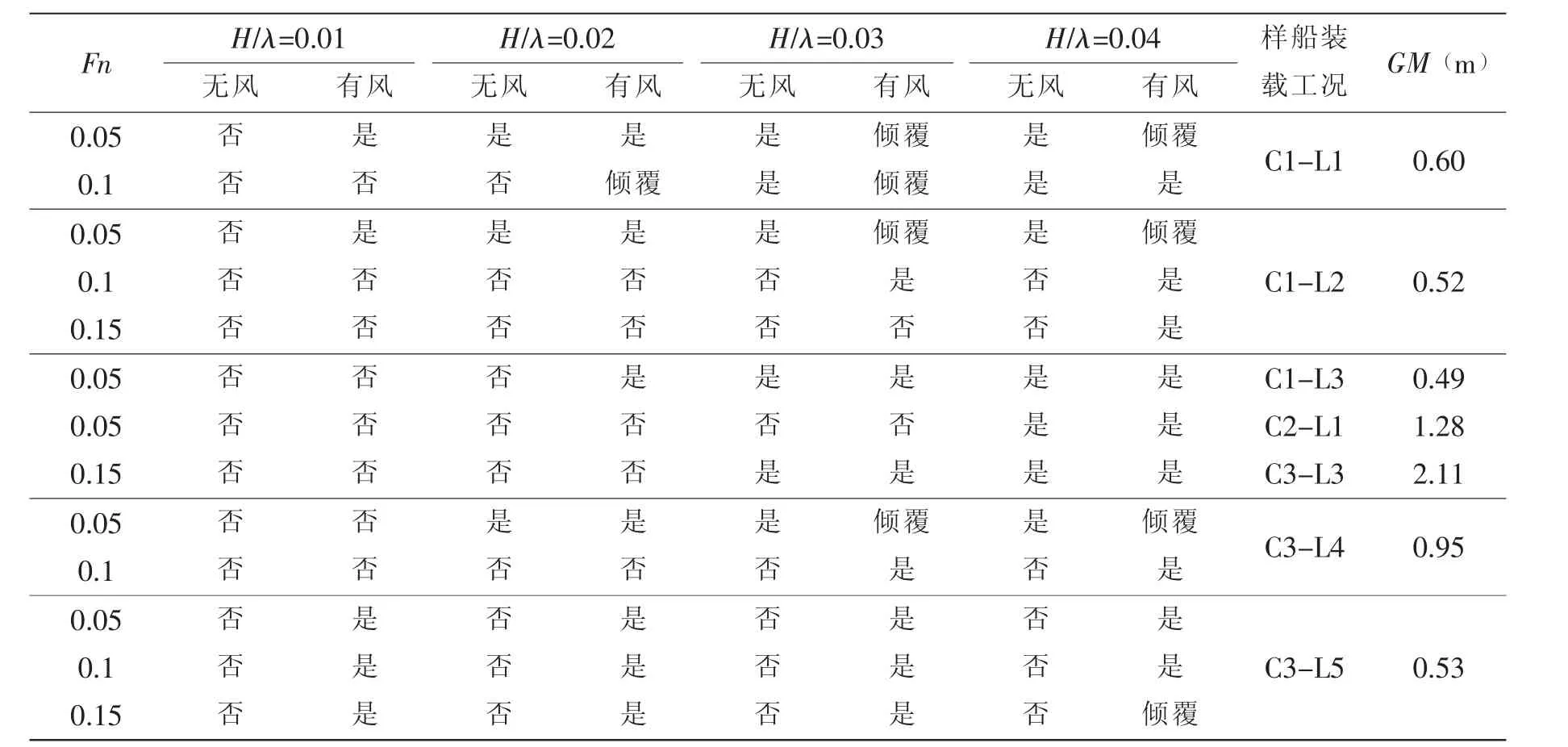
表2 對應不同GM的裝載工況參數橫搖預報結果（λ/L=1.0）Tab.2 Parametric roll prediction results of loading conditions with different GM values(λ/L=1.0)

表2給出了四艘實船的參數橫搖預報結果，未發生參數橫搖的裝載工況不予列出。判斷是否發生參數橫搖的極限橫搖角的標準值假定為25°。當橫搖角達到60°時，假定船舶將由于進水點被淹沒而傾覆。

結果表明，集裝箱船C1～C3在風載荷作用下對于參數橫搖的敏感性有所增強，風力載荷降低了誘發參數橫搖所需的入射波陡，而散貨船B1無論是否計入風載的影響均未發生參數橫搖。這一結果與實船運營記錄相符。與集裝箱船的事故相反，散貨船在惡劣海況下的實際運營中也從未報告發生過參數橫搖事故。

造成這一現象的原因在于，一方面根據IMO的研究，ΔGM/GM值較大則對參數橫搖更為敏感（ΔGM為波浪中GM的變化幅值），因此GM較大的裝載工況將會具有更強的能力抵御由于波浪中GZ值變化誘發的參數橫搖。散貨船由于其船型特點，波浪中GM的變化幅值比較小，因此對于參數橫搖現象相對不敏感，而集裝箱船船型特點決定了其波浪中GM變化幅值相對較大，當集裝箱船裝載工況的GM值較小時，ΔGM/GM值相對較大。而且由于GM較小因此抵抗外界初始擾動的能力也相對較弱，此時風載荷能夠引起相對較大的初始橫傾（見表1），因此發生參數橫搖的概率更高。對于GM值較大的裝載工況（排水量和慣性矩相似時），由于其橫搖固有頻率較大因此也相對難以滿足兩倍遭遇頻率的條件。

另一方面，由表1可見集裝箱船由于甲板裝載大量集裝箱，承受的風力載荷遠遠大于散貨船，因此風載荷對于集裝箱船的影響更為顯著。當入射波陡處于該裝載工況發生參數橫搖的臨界波陡附近時，則該裝載工況對GZ值的變化將十分敏感，此時足夠強大的風力載荷對GZ曲線的擾動將足以誘發參數橫搖甚至導致傾覆。

本文對于風載荷對實船參數橫搖預報影響的研究所采用的海況條件是基于Grim的等效波理論換算的等效規則波。對于參數橫搖響應的實船實海域短期預報，可采用ITTC雙參譜進行不規則波條件下的模擬。但由于不規則波中參數橫搖現象是非各態歷經的[25]，數值模擬也會面臨與模型試驗相似的困難，即需要進行長時間的重復多次模擬。圖7給出了對C3船的L4工況多次重復計算參數橫搖響應的示意，每次計算模擬實船在迎浪長峰波中航行1小時。風載荷對于實船短期預報的影響有待進一步研究。

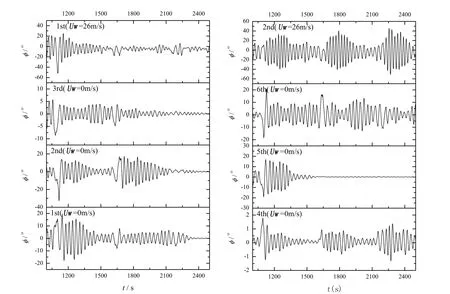
圖7 C3裝載工況L4長峰波計算示意（Fn=0.05，有義波高5.5 m，周期12.5 s）Fig.7 Simulation of parametric roll for irregular waves in head sea(Fn=0.05,Hs=5.5 m,TZ=12.5 s)

3 結 論

本文以四艘實船為研究對象，基于風浪耦合的三自由度弱非線性模型進行了規則入射波條件下參數橫搖響應的仿真計算，研究了風力載荷假定對于實船參數橫搖運動的影響。研究發現風載荷對于集裝箱船參數橫搖敏感性的影響較為顯著，對于散貨船基本沒有影響。集裝箱船GM較小的裝載工況對于風力載荷的影響更加敏感。風力載荷的引入擴大了發生參數橫搖的入射波頻率范圍，增大了參數橫搖運動的幅值，同時降低了誘發參數橫搖響應所需的入射波幅值，因此在實船預報中如果忽略風載荷的作用，有可能低估參數橫搖的發生概率。

由于風載假定對于誘發參數橫搖起到了促進作用，有助于幫助處于臨界點的裝載工況降低發生參數橫搖的門檻從而引起事故，因此當航行中有可能無法規避惡劣氣象、海況條件時對于此類裝載工況需要采取適當的操作限制措施降低發生參數橫搖的概率。

本文的研究表明了考慮氣象條件對于實船參數橫搖預報的重要性。因此未來開展實船實海域短期預報研究時，風載對于船舶參數橫搖的影響應當引起足夠的重視，探索有效的風浪聯合作用下的數值模擬和水池試驗驗證方法尤其重要。

[1]France W N,et al.An investigation of head-sea parametric rolling and its influence on container lashing systems[C].SNAME Annual Meeting,2001 Presentation.2001:1-24.

[2]China.Proposal for Level 2 criteria of parametric rolling and excessive accelerations[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session,2012:3-2.

[3]China.Sample verification and proposal of the draft level 1 criteria on parametric roll and pure loss of stability[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session,2012:3-5.

[4]W G.Report of the working group at SLF 53(part 2)[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session,2012:3-1.

[5]China.Comments on Level 2 criteria of parametric rolling(SDC 2/5/1)[C]//Ship Design and Construction 2nd Session,London:International Maritime Organization,2014:1-4.

[6]Japan.Information collected by the correspondence group on intact stability regarding the second generation intact stability criteria development(INF.8)[C]//Ship Design and Construction(SDC)1st Session,London:International Maritime Organization,2014:1-130.

[7]周耀華,張高峰,馬 寧.基于IMO二代穩性衡準的實船參數橫搖敏感性及衡準完善[J].上海交通大學學報,2016,50(3):425-436.Zhou Yaohua,Zhang Gaofeng,Ma Ning.Vulnerability check and further development of parametric roll criteria of 2nd generation of intact stability code of IMO based on full scale ship data[J].Journal of Shanghai Jiao Tong University,2016,50(3):425-436.

[8]Bulian G,Francescutto A.A simplified modular approach for the prediction of the roll motion due to the combined action of wind and waves[J].Journal of Engineering for the Maritime Environment,2004,218:189-212.

[9]Chang B C.On the parametric rolling of ships using a numerical simulation method[J].Ocean Engineering,2008,35:447-457.

[10]Germany.Further background information on the proposal by Germany with regard to the new generation intact stability criteria[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session(2012),INF.7,2012.

[11]Naoya Umeda,Hirotada Hashimoto.An investigation of different methods for the prevention of parametric rolling[J].JMar Sci Technol,2008,13:16-23.

[12]Osman Turan,Zafer Ayaz.Parametric rolling behaviour of azimuthing propulsion-driven ships[J].Ocean Engineering,2008,35:1339-1356.

[13]Juncher Jensen J,Terndrup Pedersen P,Vidic-Perunovic Jelena.Estimation of parametric roll in a stochastic seaway[C].IUTAM Symposium on Fluid-Structure Interaction in Ocean Engineering,2008:141-154.

[14]Surendran S,Lee SK,Sohn K H.Simplified model for predicting the onset of parametric rolling[J].Ocean Engineering,2007,34:630-637.

[15]楊素軍,范余明,等.大型集裝箱船參數橫搖模型試驗研究[C]//2007年船舶力學學術會議暨《船舶力學》創刊十周年紀念學術會議.中國銀川,2007:21-25.Yang Sujun,Fan Sheming,Nie Jun,et al.Model test study on parametric roll of large scale container ship[C]//2007 A-cademic Conference on Mechanics of Ships and the 10th Anniversary Commemorative Conference of ‘Ship Mechanics’.Yinchuan,China,2007:21-25.

[16]Fu L K,Jiang Z P.Numerical simulation of parametric rolling in longitudinal regular waves[J].Ship&Ocean Engineering,2007,04:34-37.

[17]常永全,范 菊,等.迎浪船舶的參數橫搖分析[J].水動力學研究與進展,A輯,2008,23(2):204-211.Chang Yongquan,Fan Ju,et al.Analysis of ship parametric rolling in head sea[J].Chinese Journal of Hydrodynamics,23(2):204-211.(in Chinese)

[18]唐友剛,鄺艷香,李紅霞.初穩性高時變特性對橫搖運動的影響[J].中國造船,2008,49(2):22-28.Tang Yougang,Kuang Yanxiang,Li Hongxia.Analysis of the influence of metacentric height fluctuations on roll motion[J].Shipbuilding of China,2008,49(2):22-28.(in Chinese)

[19]Lu Jiang,Umeda N,Ma Kun.Predicting parametric rolling in irregular head seas with added resistance taken into account[J].Journal of Marine Science and Technology,2011,16:462-471.

[20]陳京普,蘇 甲,等.集裝箱船參數橫搖的非線性時域模擬[C].第二十三屆全國水動力研討會暨第十屆全國水動力學術會議文集,2011:532-538.Chen Jingpu,Su Jia,Xu Jie,et al.A study on parametric rolling of container vessel in head waves by nonlinear time domain numerical simulations[C].Proceedings of 23rd National Conference on Hydrodynamics and 10th National Congress on Hydrodynamics,2011:532-538.

[21]Yuki Kawahara,Kazuya Maekawa,Yoshiho Ikeda.A simple prediction formula of roll damping of conventional cargo ships on the basis of Ikeda’s method and its limitation[C].Proceedings of the 10th International Conference on Stability of Ships and Ocean Vehicles,2009:387-398.

[22]Larsson Lars,et al.CFD in ship hydrodynamics-Results of the Gothenburg 2010 workshop[C].The Gothenburg 2010 Workshop,2010.

[23]W G.Report of the working group at SLF 55(part 1)[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)55th session.Annex 1,2013:1-6.

[24]Grim O.Beitrag zu dem problem der sicherheit des schiffes in seegang[J].Schiff und Hafen,1961:490-497.

[25]Fossen T I,Nijmejer H.Parametric resonance in dynamical systems[M].2012:45-59.