一道高考選擇題壓軸題的多維度解法

李鳳迎

(河北省武邑縣職教中心 053400 )

A.0 B.mC.2mD.4m

分析本題是全國高考試題選擇題最后一道題，作為一道壓軸試題，它具有明顯的選拔性功能，有很強的區分度.在惜時如金的考場上，能否順利解出該題，可以說關系著考生個人的前途和命運.因考生的理解能力和解決問題能力的不同，使得對該題的解決方法也會呈現出多種精彩紛呈的思維亮點.充分發掘和利用題目中已知或隱藏的“對稱性”，將其作為解決復雜問題的重要突破口，實現解題途徑的最佳化.下面我們介紹幾種學生比較好理解又便于接受的方法，以供參考.

解法1 特殊函數法

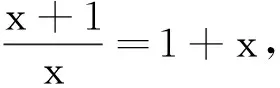
點評根據我們平時所積累的數學經驗，我們可以通過將已知抽象函數f(-x)=2-f(x)(x∈R)賦予為我們熟悉的具體函數f(x)=1+x，從而使得較為復雜的問題變得簡單化，這正是一種解決問題的快捷有效方法.該種方法簡潔明快，易于理解.

解法2 圖象平移法

點評這種方法的解題依據是利用函數圖象的平移規律.我們知道，圖象平移不改變圖象的形狀.將具有對稱性的奇偶函數的圖象通過平移就可以獲得軸對稱型函數圖象解題關鍵是找出平移之前的函數解析式并判斷它們的奇偶性，進而判斷平移之后的函數圖象的交點的橫坐標之和和縱坐標之和相對于平移之前的變化情況，進而使得問題得以解決.解題難點是對原函數的分離和對于函數的平移規律的理解.

解法3 中心對稱法

點評這種方法的解題依據是利用函數圖象的對稱性.解題關鍵是通過對函數結構的認真觀察和思考，找出函數y=f(x)圖象的對稱中心，進而根據中點坐標公式解決.解題難點是利用f(-x)=2-f(x)對原函數圖象的對稱中心的尋找和判定.

綜上，對函數奇偶性和圖象對稱特點的考查永遠為高考核心考查知識，數形結合和轉化思想永遠為高考核心思想方法，思維能力和計算能力永遠為高考核心解題手段.加強這種方法的練習成為當務之急.

參考文獻：

[1]人民教育出版社,課程教材研究所,中學數學課程教材研究開發中心. 普通高中課程標準實驗教科書( 必修) 數學4(A 版)[M]. 北京:人民教育出版社,2014.