櫻桃好吃樹難栽方程組好列解難求

董鳳娥

(河北省唐山市豐潤區任各莊鎮中學 064012)

一、問題的提出

勻變速直線運動問題，是初學高中物理的學生所接觸的第一類重要的計算.因為受小學、初中數學中有關路程類問題的多年影響，還受初中物理學過的勻速直線運動物理問題的影響，再加上數學計算、數形結合及其空間想象能力較差等因素的制約，總有一部分人不能較好的適應新出現的“加速度”、“位移”等基本概念和有關運動學公式及其推論等對解決此類問題所起的重要作用.這就致使部分人在解答此類問題時，有一種似曾相識的感覺，可就是算不對.怎樣才能突破這種“瓶頸”，達到“柳暗花明又一村”的境界呢？下面，本文以一道典型高考題為例，從物理和數學兩個維度，探究這類題的解題策略.

二、探究的過程

題目(2008年全國高考理綜)已知O、A、B、C為同一直線上的四點，AB間的距離為L1，BC間的距離為L2.一物體自O點由靜止出發，沿此直線做勻加速運動，依次經過A、B、C三點.已知物體通過AB段與BC段所用時間相等.求O與A的距離.

解法1 應用兩次位移公式和一次位移速度關系式，建立方程組.

設物體的加速度為a，經過A點時的速度為v0，經過AB段和BC段的時間為t，以物體在AB段和AC段的運動為研究對象，根據位移公式可得：

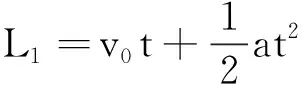
L1+L2=2v0t+2at2

②

以物體在OA段的運動為研究對象，根據位移速度關系公式得：

③

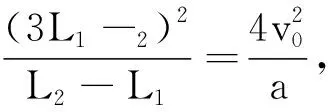
解法2 應用三次位移公式求時間，利用時間等量建立方程.

設物體運動的加速度為a，OA段位移為s，物體在OA段、OB段、OC段運動時間分別為t1、t2、t3.以物體在OA段、OB段、OC段的運動為研究對象，根據位移公式可得：

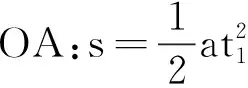
①

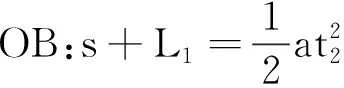
②

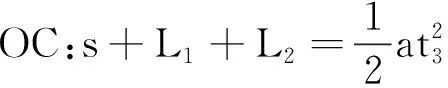
③

已知物體在AB段與BC段所用時間相等，所以有t2-t1=t3-t2成立，即：

整理可得無理方程：

點評此解法抓住已知條件，利用物理知識導出一個方程進行求解.看似不需要較強的數學技巧，其實不然.因為在初中數學課本中，把無理方程刪掉已經至少有十幾年了，學生解無理方程不會一帆風順.從這個角度來說，指導學生“掌握無理方程的解法”非常重要而且緊要.

解法3 應用三次位移公式，建立方程組.

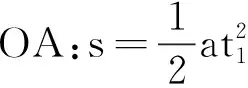
①

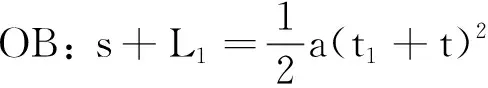
②

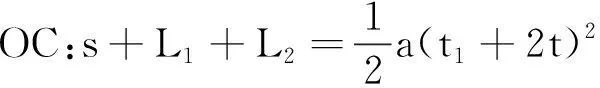
③

解法4 用鄰等時內位移差等、位移公式和位移速度關系式，建立方程組.

設物體加速度為a，經過A點時的速度為v0，經過AB段和BC段的時間為t，利用“做勻變速直線運動的物體，在相鄰相等時間內的位移之差相等”，即ΔSn+1-ΔSn=at2成立.據此可得：

L2-L1=at2

①

以物體在AC段的運動為研究對象，根據瞬時速度和位移公式可得：

L1+L2=2v0t+2at2

②

以物體在OA段的運動為研究對象，根據位移速度關系公式得：

③

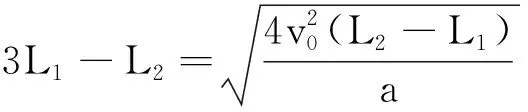
解法5 用平均速度、中時瞬時速度、鄰等時內位移差等、位移速度關系式，建立方程組.

設物體的加速度為a，經過A點時的速度為v0，經過AB段和BC段的時間為t，以物體在AC段的運動為研究對象，由平均速度公式可得：

①

②

又因為“做勻變速直線運動的物體，在相鄰相等時間內的位移之差相等”，即ΔSn+1-ΔSn=aT2成立.據此可得：L2-L1=at2

③

④

點評解方程組時，由①②顯然可得L1+L2=2v0t+2at2⑤，接下來聯立③④⑤求解，過程同解法四如出一轍.仔細品味，本解法比解法四還要高明，高明之處在于，把勻變速直線運動所涉及到的多數基本概念、基本公式，結合課本習題得到的性質、結論和推論等，完美的綜合了在一起，很有物理的“味”道.真是具有“王者風范”，我們應該為之點贊.

解法6 用速度時間關系圖像的幾何意義和相似三角形性質，建立方程組.

圖

設物體經過A、B、C三點時，對應的時刻分別為t1、t1+t和t1+2t，則物體運動的v-t圖像如圖所示.根據v-t圖像的物理意義可知，三角形的面積表示對應時刻位移的大小.因此，包含位移OA、OB、OC的各直角三角形的面積，分別等于位移OA、OB、OC的大小.顯然三個直角三角形是相似的，根據相似三角形的面積比等于相似比的平方可得：

①

②

點評本解法有一種給人“眼前一亮”的那種感覺，非常獨特.其實，它就在課本中，并且出現頻率還很高，可為什么有很多人就是想不到呢？因此，掌握 圖像和 圖像的物理意義很重要.今天解題用到了“圖像法”，明天、后天還會用到.至于方程組的解法，見解法二的點評，不再累述.

三、得出的結論

1.構建知識體系，形成思維導圖

如果不考慮勻速直線運動和以后將要學習的平拋、

斜拋、自由落體、豎直上拋等運動，就目前而言，勻變速直線運動的知識主要包括：定義、特點和分類，位移和時間之間的關系，速度和時間之間的關系，位移和速度之間的關系，重要性質和推論，常用的比例關系式，等等.

把這些知識構建成一個體系，和平時做題積累的一些解題技巧融合在一起，形成“思維導圖”，在頭腦中不斷進行存儲、補充、完善和強化.只有養成這樣的好習慣，今后解題時，才能迅速從大腦中提取相關的公式、性質、推論、圖像、比例等知識和常見解題技巧.

2,通過解題實踐，總結方程(組)解法

本題的各種解法有一個共同之處，那就是建立方程組，而解方程組恰恰就是大家的短板.因此，解決和勻變速直線運動有關的問題時，一定要樹立方程組的數學思想，養成用數學思維親自進行推算的習慣，不要嫌麻煩.尤其要注意通過類似本題的解法探究，不斷總結方程和方程組的解法，這才是解決此類問題最常用的一把利器，也是今后研究物理問題必備的一種數學素養.

參考文獻：

[1]王后雄. 教材完全解讀( 高中物理必修2)[M].北京:中國青年出版社,2013(9).