小型無人直升機反步自適應控制

周 健，王 敏，洪 良，李 珣

ZHOU Jian,WANG Min,HONG Liang,LI Xun

西安工程大學 電子信息學院，西安 710048

School of Electronics and Information,Xi’an Polytechnic University,Xi’an 710048,China

1 引言

隨著計算機技術、通訊技術的迅速發展以及各種數字化、體積小、測量精度高的新型傳感器不斷面世，小型無人直升機系統的研制受到了廣泛關注。小型無人直升機是一種強非線性、高度耦合和具有不確定性影響的復雜系統，因此，在進行飛行控制系統設計時應采用非線性控制的方法處理時變耦合的動力學模型。小型無人直升機飛行控制系統設計實際就是解決多輸入多輸出系統存在不確定性時的魯棒性設計問題。

近年來，由Kokotovic P V等人發展起來的反步（Backstepping）控制設計方法[1]在處理非線性問題時顯示出獨特的優越性，特別是針對級聯線性或非線性系統，通過選取合適的 Lyapunov函數，在構造輔助控制輸入的同時補償不確定性的影響，最終得到穩定的控制律，反步法在不確定非線性系統控制設計中引起了廣泛關注，并且在航空航天領域得到了應用[2-7]。反步法與神經網絡相結合可以解決一類不確定非線性系統的設計問題[8-9]。文獻[10]針對一類非線性系統，設計了基于神經網絡的反步控制器，但Lyapunov函數的選擇復雜；Kendoul基于無人直升機的非線性模型采用反步控制方法設計姿態控制器，所設計的控制器在閉環系統中雖具有漸近穩定的性能，但存在較大的控制誤差[11]。

本文提出一種基于CMAC神經網絡的小型無人直升機反步自適應姿態控制器設計方法。針對具有復雜動力學特性的小型無人直升機非線性動力學模型，采用CMAC神經網絡在線學習系統不確定性以及反步控制中各階虛擬控制量的導數信息，同時設計魯棒控制項克服CMAC神經網絡在線學習系統不確定性的誤差，根據系統狀態誤差和神經網絡參數估計誤差構造Lyapunov函數遞推設計小型無人直升機反步自適應控制器，并在懸停以及小速度前飛模態下對所設計的控制器進行仿真以驗證設計方法的有效性。

2 小型無人直升機動力學模型

本文研究對象為自主研制的小型無人直升機系統[12]，如圖1所示。控制的目的是在懸停以及小速度前飛模態下實現姿態指令θ、φ的跟蹤。小型無人直升機機體運動是由周期變距輸入δlat和δlon通過旋翼產生的揮舞傳遞至槳轂產生相應的力和力矩的變化，進而引起機身產生線速度和角速率的變化，最終實現姿態和位置的變化。忽略對軸向影響較小的氣動力導數，構成小型無人直升機姿態控制系統的非線性動力學模型如下：

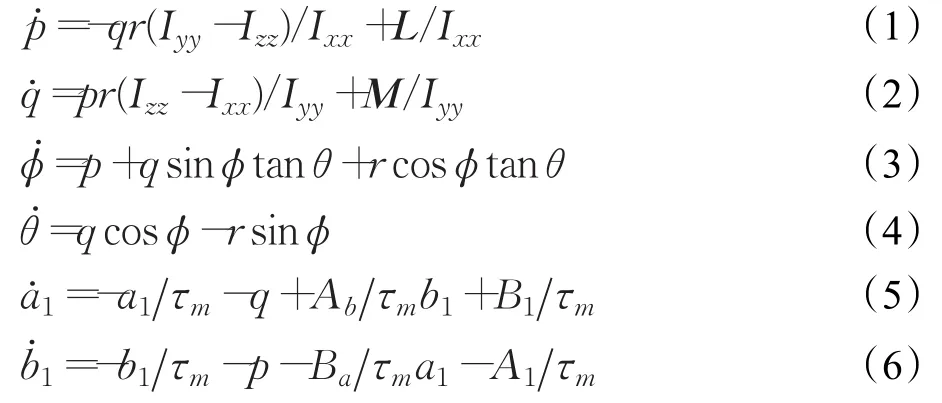
式中，p、q為機體坐標系下機身的角速度；L、M為力矩矢量；θ、φ為俯仰角和滾轉角；a1、b1為縱向揮舞角和橫向揮舞角；Ixx，Iyy，Izz為機體坐標系中繞軸的轉動慣量；為主旋翼響應的時間常數，γ為洛克系數，Ω為主旋翼轉速；A1和B1分別為橫向周期變距輸入和縱向周期變距輸入；Alon和Blat分別表示為主旋翼橫縱向周期變距輸入與揮舞角橫縱向輸出之間的有效增益系數。

圖1 小型無人直升機系統

根據小型無人直升機的控制輸入與響應輸出的特點，需要設計姿態角指令跟蹤控制律u，使系統輸出y穩定跟蹤給定的輸入信號yr，有效抑制不確定項Δ1、Δ2、Δ3對系統的影響，因此，將小型無人直升機的數學模型寫為如下形式：

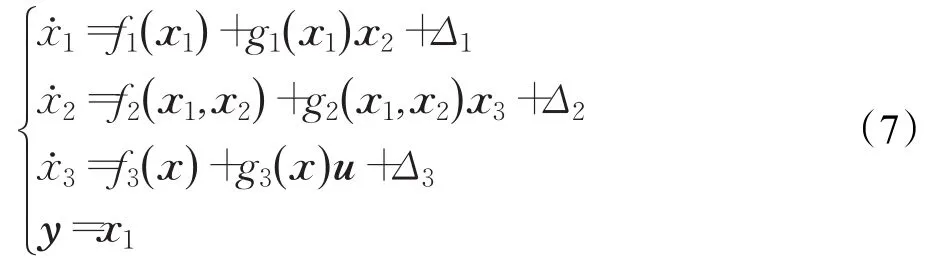
其中，狀態變量，控制變量為縱向控制輸入和橫向控制輸入。定義。在實際飛行過程中，狀態矩陣中的氣動導數實際為多個狀態變量的非線性函數，不能精確已知，因此，由建模誤差等因素產生的系統不確定項可表示為：

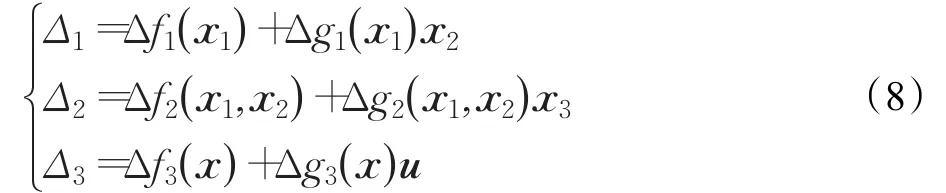
其中，Δf1、Δf2、Δf3、Δg1、Δg2、Δg3表示建模誤差。

3 反步自適應控制器設計

3.1 反步自適應控制器結構

CMAC是一種表達復雜非線性函數的表格查詢型自適應神經網絡[13-15]，其實質是一種查表技術，CMAC神經網絡把信息存儲在局部的結構上，在保證函數逼近的前提下，具有學習速度快、結構簡單，易于軟硬件實現的特點。

為了提高小型無人直升機的控制精度，本文提出一種采用CMAC神經網絡與反步自適應控制相結合的控制器設計方法，其結構如圖2所示。從圖中可以看出，反步控制方法將每一個子系統（如式（7））中的x1,x2,x3作為虛擬控制輸入，通過設計適當的虛擬反饋xi+1=ai(x1,x2,…,xi)，使得前面的子系統得到鎮定，且狀態達到漸近穩定，但系統的虛擬反饋一般并不可得。因此，可引入誤差變量zi+1=xi+1-ai(x1,x2,…,xi)，通過控制輸入的作用，使得xi+1漸近收斂于ai(x1,x2,…,xi)，從而實現整個系統的漸近穩定，同時，通過設計CMAC神經網絡在線逼近系統不確定性以及反步控制中各階虛擬控制量的導數信息，使系統輸出可漸近跟蹤期望輸出x1r，進而提高系統的控制精度。

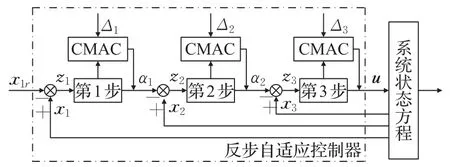
圖2 反步自適應控制器結構圖

3.2 控制器設計

在設計控制器之前，先給出與系統控制律設計相關的定義和假設：

假設1期望的參考信號有界且一階導數有界。

假設2矩陣可逆。

首先，考慮閉環系統（7）的第1個子系統，引入跟蹤誤差狀態變量：

式中，a1為理想的中間級虛擬控制量。

設計CMAC神經網絡在線逼近系統不確定性：

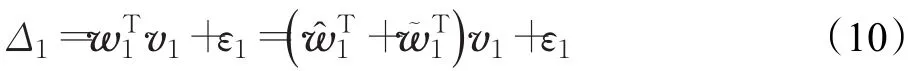
式中，1=w1-，w1為期望權值矩陣，為權值向量矩陣的估計，ε1為理想逼近誤差，為誤差權值向量矩陣，即估計權值向量矩陣與期望權值向量矩陣的誤差。對z1求導，可得：

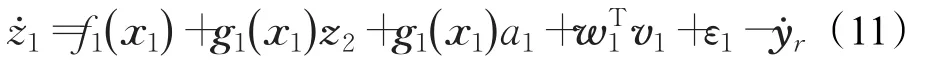
選取第一個子系統的理想虛擬控制量為：

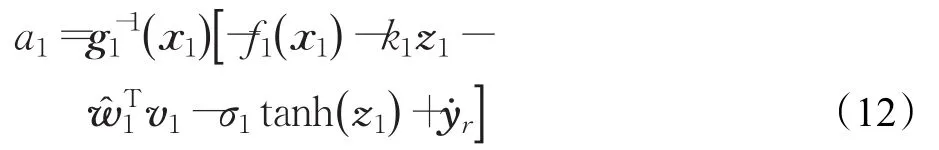
由于Δ1期望權值w1未知，得不到理想的a1，因此用估計值代替期望權值w1。上式中k1和σ1為正實數；σ1tanh(z1)為設計的魯棒項，用以抵消逼近誤差ε1的影響。為避免控制量的不連續，用雙曲正切函數tanh()代替符號函數sgn()。

將公式（12）代入至公式（11）可得：

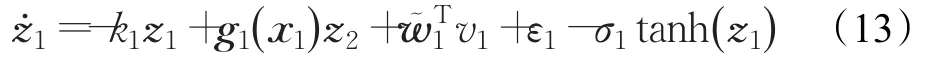
選取Lyapunov函數：

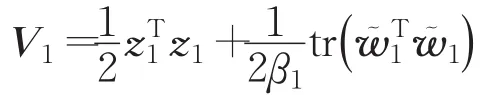
對V1求導可得：

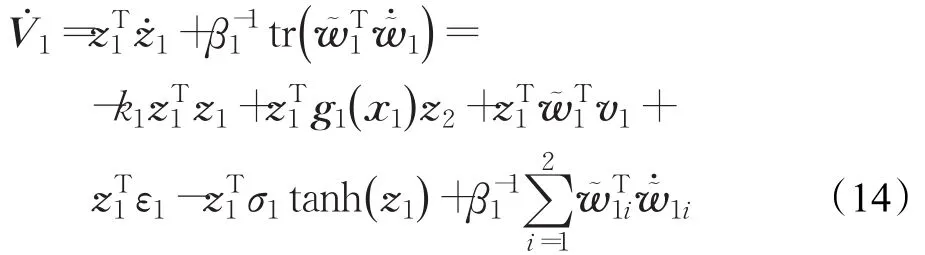
選擇CMAC神經網絡自適應權值調整規則為：，其中 0＜β1＜2 ，將其代入式（14）：

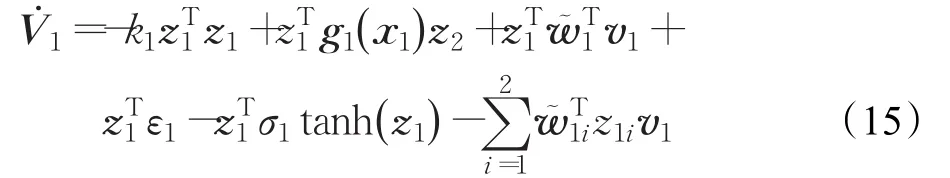
式中下標中的1表示第1步誤差權值向量矩陣，i表示其中的i個列向量；v1表示第一步m維相聯空間A中的向量；z1i下標中的1表示第1步得到的輸出誤差向量，i表示其中的i個元素，i=1,2,…,n。由于：

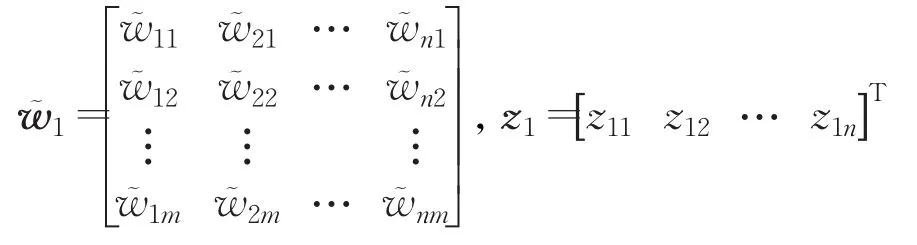
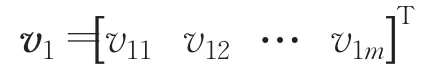
因此，公式（15）中項可寫為：

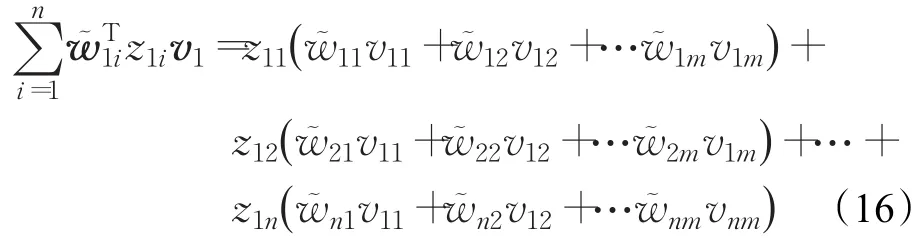
公式（15）中項可寫為：

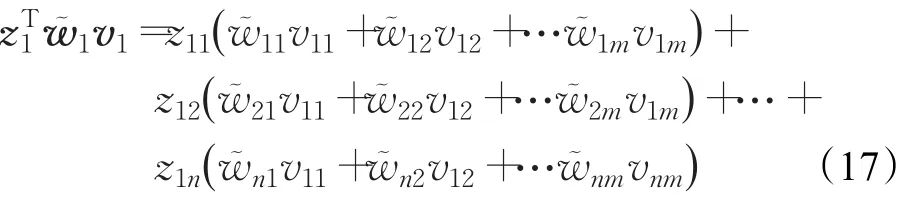
可以得到：，將其代入公式（15）中：

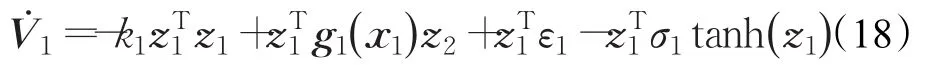
由于a1不是最終的控制信號，因此需要第二步設計，對z2求導得：

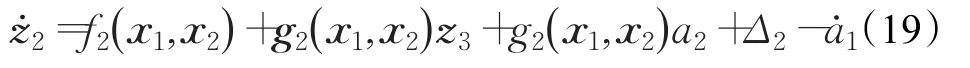
設計CMAC神經網絡在線逼近系統不確定性：

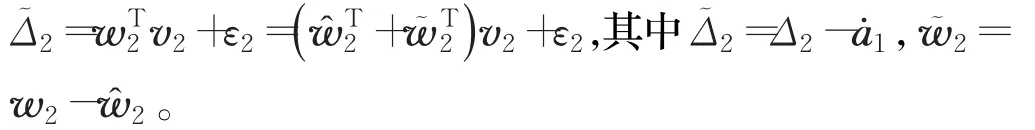
選取理想的中間級虛擬控制量：

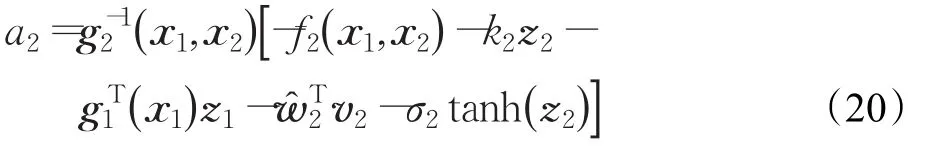
由于Δ2期望權值w2未知，得不到理想的a2，因此用估計值w2代替期望權值w2。σ2tanh(z2)為設計的魯棒項，用以抵消逼近誤差ε2的影響。

將公式（20）代入公式（19）中：

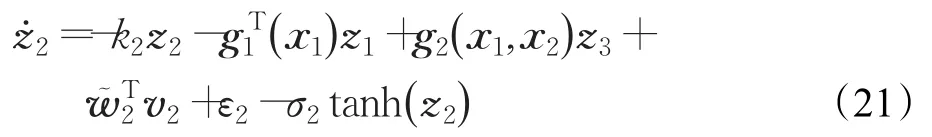
選取Lyapunov函數：

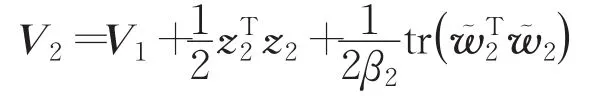
選擇CMAC神經網絡自適應權值調整規則：，其中 0＜β2＜2。

對V2求導可得：

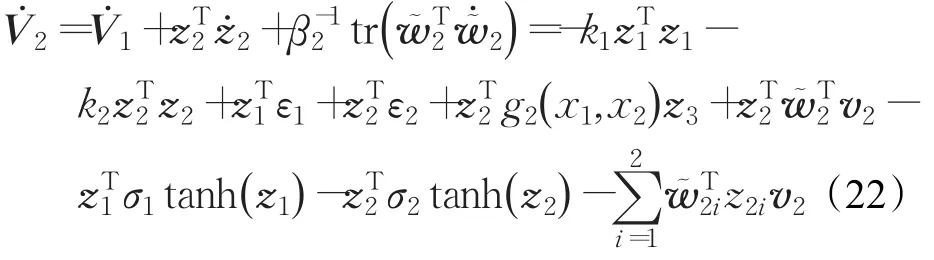
根據公式（16）、（17）同理推導可得：，將上式代入公式（22）中：

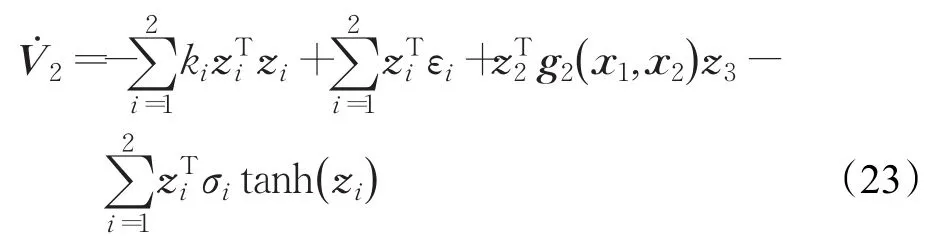
考慮閉環系統（7）的第3個子系統Δ3，定義虛擬反饋誤差z3=x3-a2對z3求導，可得：

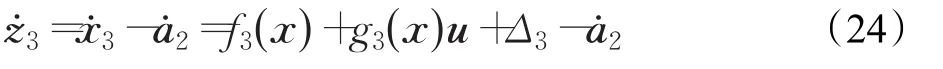
設計CMAC神經網絡在線逼近系統不確定性：，其中

設計系統的控制輸入為：

由于Δ3期望權值w3未知，得不到理想的控制輸入u，因此用估計值代替期望權值w3。σ3tanh(z3)為設計的魯棒項，用以抵消逼近誤差ε3的影響。

將公式（25）代入公式（24）中：

選取Lyapunov函數：

選擇CMAC神經網絡自適應權值調整規則：，其中，0＜β3＜2。

對V3求導可得：

根據公式（16）、（17）可以同理推導得到：zT3w3v3=，將其代入公式（27）中：

當選擇時有：

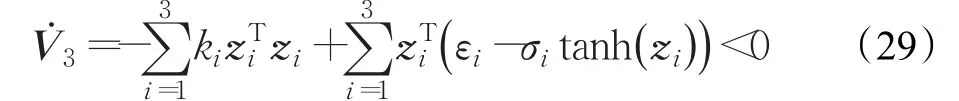
因為＜0，所以V3漸近收斂于零，即 z1，z2，z3漸近收斂于零，從而系統實際輸出漸近收斂于期望輸出yr。對小型無人直升機系統設計公式（12）和公式（20）作為虛擬反饋輸入，公式（25）作為連續控制輸入，采用式描述的CMAC神經網絡在線逼近系統的不確定項，學習規則：，選擇為設計的魯棒控制項，用以抵消神經網絡在線逼近誤差εi(i=1,2,3)的影響，則當所設計的魯棒控制項系數(下標i表示第i步得到的神經網絡輸出誤差向量，j表示其中 j個元素），系統輸出可漸近跟蹤期望輸出，且系統實際控制輸入連續。

4 仿真驗證與分析

選取小型無人直升機飛行仿真初始狀態為穩定懸停狀態，即V0=0 m/s，θ0=φ0=0°?，飛行高度h0=100 m 。CMAC神經網絡主要參數：學習速率β=0.2，泛化參數C=50，N=1 000；反步自適應控制器主要參數：σ1=0.2，σ2=0.1，σ3=2，k1=30，k2=10，k3=2。仿真目標為在未建模動態的影響下驗證姿態角跟蹤參考指令信號的響應性能。

取參考指令：，其他時刻為配平值。需要說明的是，為了避免跟蹤指令發生階躍突變，在參考指令信號后增加了一個時間常數為0.5 s的一階慣性濾波器得到期望的跟蹤指令。基于神經網絡的反步自適應姿態控制器響應輸出曲線如圖3所示，左側為縱向[θ,q,a1]的響應曲線，右側為橫向[φ,p,b1]的響應曲線，由仿真結果可知，反步自適應控制器能夠快速、準確地跟蹤參考指令，角速率p,q和揮舞角a1,b1以及圖4所示的控制輸入δlat,δlon信號均在合理的限幅之內，滿足仿真目標要求。

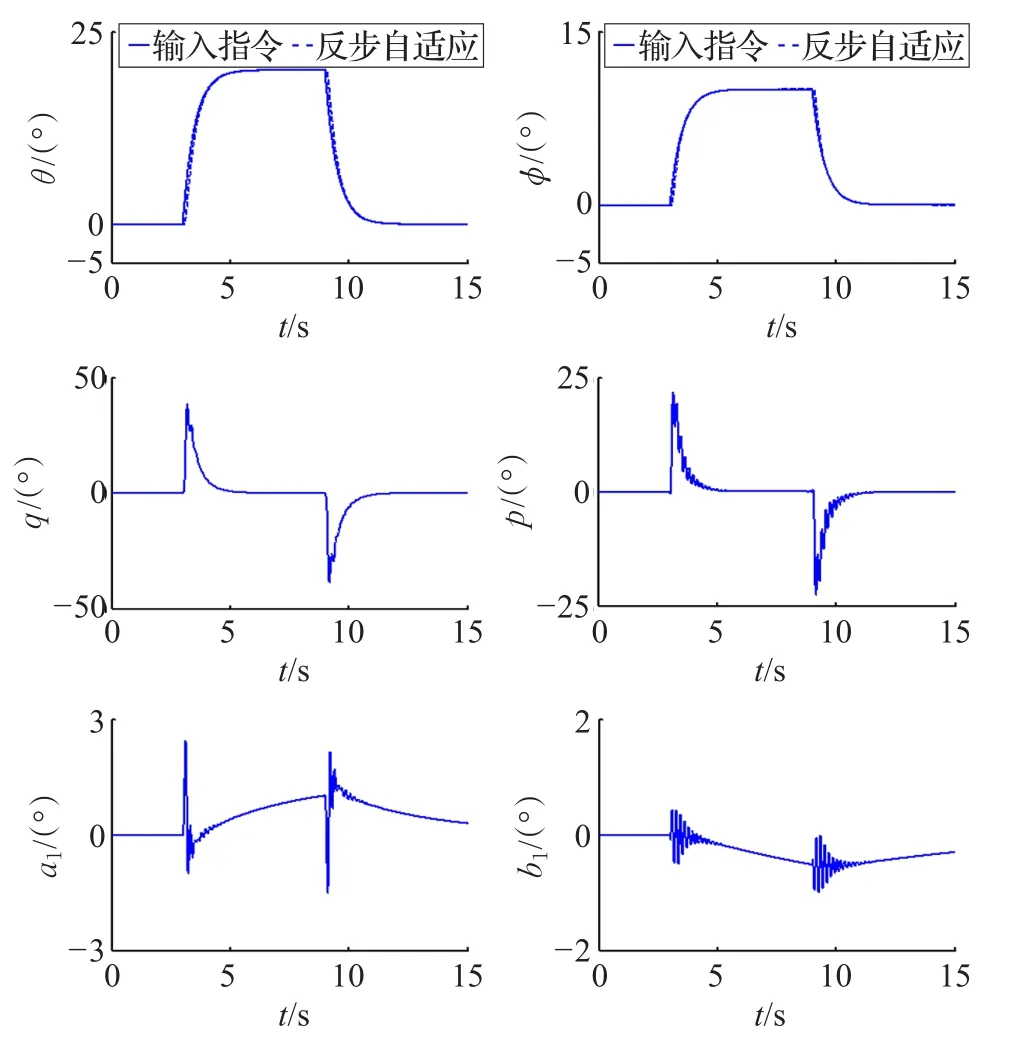
圖3 反步自適應控制器響應曲線

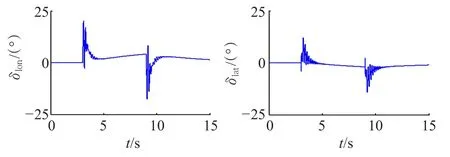
圖4 縱向、橫向控制輸入曲線

設計小型無人直升機PID控制器，在相同的仿真條件下，PID控制器參數為：縱向kp=13.5、kd=3.6；橫向kp=9.8、kd=4.3，仿真響應曲線如圖5所示。從仿真結果可以看出，反步自適應控制器的跟蹤的縱向最大誤差小于 3.62°?，橫向最大誤差小于 1.59°?，而PID控制器的縱向最大跟蹤誤差小于6.89°?，橫向最大跟蹤誤差小于2.6°?。所設計反步自適應姿態控制器動態響應效果較好，在快速性、準確性和穩定性上要優于PID控制方法所設計的姿態控制器。

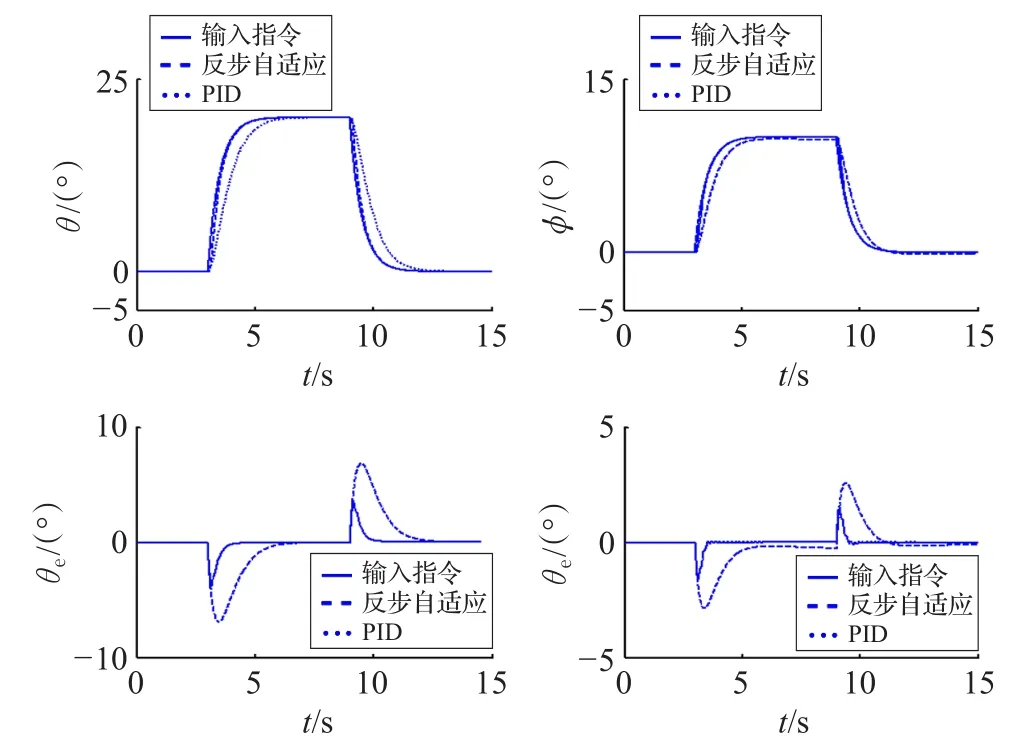
圖5 兩種控制方法比較的響應曲線

圖6 為系統模型參數攝動50%和120%的情況下跟蹤參考指令信號：，其他時刻為配平值時的響應曲線。由圖6可見，在模型參數攝動情況下，反步自適應控制器依然能快速跟蹤指令信號，在具有跟蹤實時性好、跟蹤誤差較小的同時還有較強的魯棒性，并且控制輸入δlat,δlon均在合理的控制輸入限幅之內。

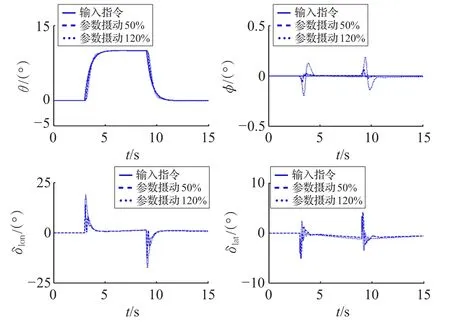
圖6 模型參數攝動時的響應曲線

5 結論

本文提出了一種基于神經網絡的反步自適應控制器設計方法以解決小型無人直升機飛行時模型嚴重非線性和參數不確定性問題。將所設計的控制器在小型無人直升機姿態控制系統中應用并進行仿真驗證，仿真結果表明，所設計的控制器在有效抑制系統不確定影響的同時還具有響應迅速以及良好的指令跟蹤性能，并且在模型參數攝動較大時，該控制器仍可以跟蹤參考指令并表現出較強的魯棒性。

參考文獻：

[1]Krstic M，Kokotovic P V.Control Lyapunov functions for adaptive nonlinear stabilization[J].Systems and Control Letters，1995，26（1）：18-23.

[2]Francesc P，Faycal I，Jose R.Numerical issues in backstepping control：Sensitivity and parameter tuning[J].Journal of the Franklin Institute，2008，345（8）：891-905.

[3]Hsu C F，Lin C M.Fuzzy-identification-based adaptive controller design via backstepping approach[J].Fuzzy Sets&Systems，2005，151（1）：43-57.

[4]Nurkan Y，Yuksel H.Backstepping control of a vehicle with active suspensions[J].Control Engineering Practice，2008，16（12）：1457-1467.

[5]Ozbay U，Zergeroglu E，Sivrioglu S.Adaptive backstepping control of variable speed wind turbines[J].International Journal of Control，2008，81（6）：910-919.

[6]孫勇，章衛國，章萌.基于神經網絡的反步自適應大機動飛行控制[J].系統工程與電子技術，2011，33（5）：1113-1117.

[7]劉少華，周志久，段征宇.戰斗性機動飛行的智能反步自適應控制[J].飛行力學，2011，29（6）：22-25.

[8]Zou Y，Zheng Z.A robust adaptive RBFNN augmenting backstepping control approach for a model-scaled helicopter[J].IEEE Transactions on Control Systems Technology，2015，23（6）：2344-2352.

[9]Chang Guanqing，Qian Hanbo，Fan Guoliang，et al.Adaptive fuzzy backstepping control for a miniature helicopter[C]//International Conference on Automation and Logistics，2010：451-456.

[10]Lin F J，Shieh P H，Chou P H.Robust adaptive backstepping motion control of linear ultrasonic motors using fuzzy neural network[J].IEEE Transactions on Fuzzy Systems，2008，16（3）：676-692.

[11]Kendoul F.Nonlinear hierarchical flight controller for unmanned rotorcraft：Design，stability，and experiments[J].Journal of Guidance，Control，and Dynamics，2009，32（6）.

[12]周健，洪良，李文超.小型單旋翼無人直升機系統的設計與實現[J].西安工程大學學報，2014，28（5）：626-630.

[13]蘇剛，陳增強，袁著祉.小腦模型關節控制器（CMAC）理論及應用[J].儀器儀表學報，2003（S1）：269-273.

[14]Pinzon Morales R D，Ohata Y，Hirata Y.Adaptive control of 2-wheeled balanced robot by cerebellar neuronal network model[J].Engineering in Medicine and Biology Society，2010：1589-1592.

[15]Kim Daijin.A design of CMAC-based fuzzy logic controller with fast learning and accurate approximation[J].Fuzzy Sets and Systems，2002，125：93-104.