反艦導彈的超前動態抗飽和控制器設計與仿真?

潘長鵬 趙紅超 王 亭

（海軍航空大學 煙臺 264001）

1 引言

控制系統的Windup現象，是由于被控對象的輸入受限，使得被控對象的實際輸入與控制器的輸出不相等，引起閉環系統響應變差（如超調變大、調節時間變長、甚至系統失去穩定性）的現象。為了克服Windup現象，保證控制系統的良好品質，需要在控制器設計中加入抗飽和（Anti-Windup）設計算法［1］。國內外研究者針對工業控制系統的輸入受限問題已進行了大量研究，提出了許多不同形式的抗飽和控制器設計算法［2～7］。

反艦導彈的過載控制系統中同樣存在Windup現象，由于能量有限或者機械強度限制，執行機構的工作存在飽和約束［8～9］。當執行機構工作達到飽和值時將會導致有效控制力矩顯著不足，進而引起導彈控制系統品質下降甚至不穩定。前期我們對導彈控制系統抗飽和設計方案進行了初步研究，通過仿真分析發現，當采用靜態抗飽和算法時，雖然能夠減小系統輸入量的大小，但是減小以后的值仍然超過飽和值，執行機構并沒有脫離飽和工作狀態。當采用動態抗飽和算法時能夠在一定程度上將系統輸入量減小到飽和值以下，使執行機構飽和工作狀態時間減小52%以上。那么，有沒有更好的抗飽和算法能夠使執行機構完全脫離飽和工作狀態呢？

文獻［10～11］對抗飽和機構的三種激活方式進行了詳細研究，即立即激活方式、超前激活方式和滯后激活方式。通過仿真結果比較，證明了超前激活方式的抗飽和性能優于立即激活方式和滯后激活方式，而且，超前激活方式還能夠擴大系統原點的吸引域。借鑒上述研究成果，本文將前期設計的動態抗飽和算法改進為超前激活方式（簡稱為超前動態抗飽和算法），進一步研究反艦導彈過載控制系統中的超前動態抗飽和控制器設計方案，以實現導彈執行機構完全脫離飽和工作狀態的目標。

2 反艦導彈運動模型

超聲速反艦導彈具有軸對稱氣動外形，其俯仰通道和偏航通道的結構是基本一致的；滾動通道僅起穩定作用，維持滾動角為零。俯仰通道和偏航通道采用過載控制系統，下面以俯仰通道為例進行研究。反艦導彈采用了沖壓發動機，其正常工作要求反艦導彈的攻角和側滑角都為小角度，在小角度條件下可以進行線性化處理，從而建立反艦導彈俯仰通道的運動模型如下：

式中：為建模誤差，都是有界量；彈體過載ny為系統輸出量；其它各個變量的物理意義參見《導彈飛行力學》［12］。

將作為執行機構的舵機系統視為一階慣性環節，即

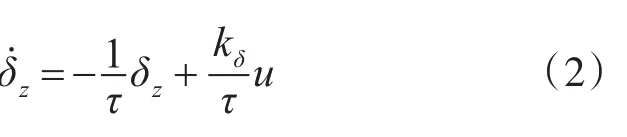
式中：τ為舵機系統的時間常數；kδ為放大系數；u為系統輸入量，即送入舵機的電壓信號。實際上，u是受到飽和限制的。

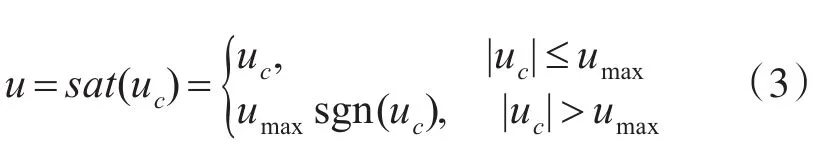
式中：uc是控制器的輸出，即控制算法解算得出的值；umax為送入舵機的電壓最大值。uc經過飽和環節后成為實際的系統輸入u。為了便于分析，在運動模型建立時先不考慮飽和環節。

將式（1）的第3個方程代入第1個方程，整理可得

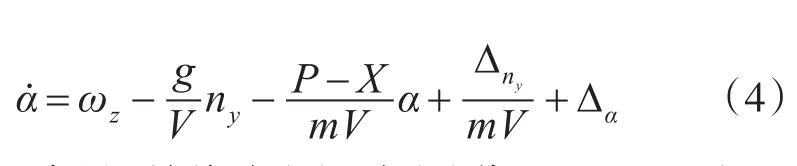
對ny求導，并將式（2）、式（4）代入，整理可得

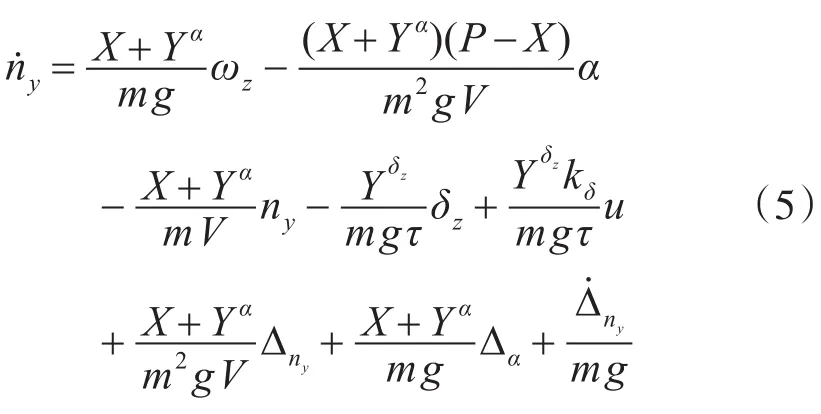
利用容易測量的導彈狀態量過載ny和角速度ωz來設計控制系統，以ny和ωz的線性組合構造組合狀態量ξm，并將其作為系統的新輸出量［8～9］

對ξm求導，并將式（5）和式（1）的第2個方程代入，整理可得

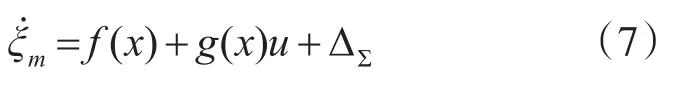
式中：

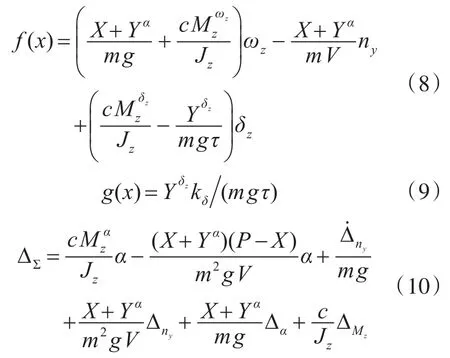
f(x)和g(x)為已知量；ΔΣ稱為“匯總不確定項”，由于α是不可測的未知量，因此含有α的項也是不確定項。

3 擴展狀態觀測器設計

針對匯總不確定項，采用擴張狀態觀測器來設計估計器。將匯總不確定項ΔΣ看作是未知的被擴張的狀態變量：ξm2=ΔΣ，并設其中：ζ(t)是未知函數，由此式（7）變換為

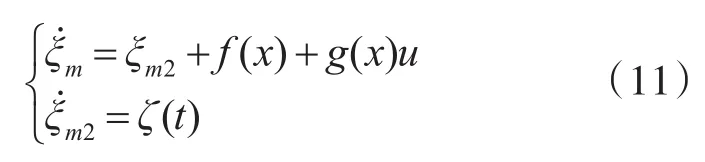
擴張狀態觀測器設計為［13］

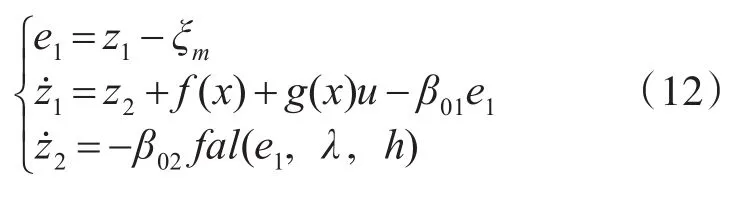
式中：β01＞0，β02＞0，0＜λ＜1，0＜h＜1；fal函數的表達式為

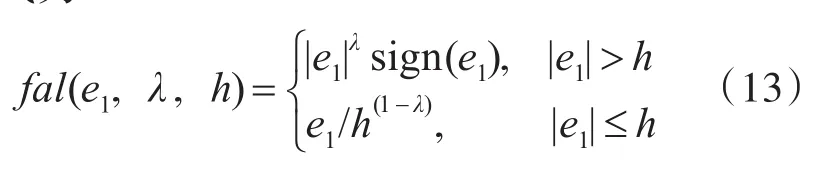
設e2=z2-ξm2，由文獻［13］的研究可知，當系統進入穩態時，估計誤差滿足：

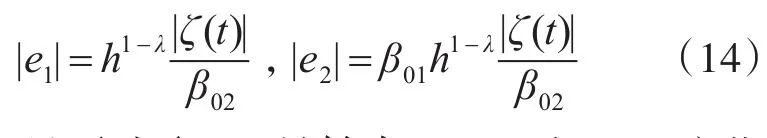
因此，只要選取β02足夠大于ζ(t)和β01，這些估計誤差都會很小；從而擴張狀態觀測器中的狀態z2能夠很好地估計匯總不確定項ΔΣ。因此，在下面的控制器設計中將以z2代替式（7）中的ΔΣ。

4 控制器設計

控制器設計采用國內外研究者們常用的二步法設計方法，即首先不考慮執行機構的飽和限制，設計出滿足系統性能指標的標準控制器；然后加入超前動態抗飽和補償算法，克服非線性飽和因素引起的不良影響，起到抗飽和的作用。

4.1 標準控制器設計

首先不考慮執行機構的飽和限制，認為u=uc。考慮到滑模控制方法對參數攝動和外界干擾等具有強魯棒性，下面采用滑模控制方法來設計標準控制器。設ny，ωz，ξm的指令信號分別為nyc，ωzc，ξmc；則

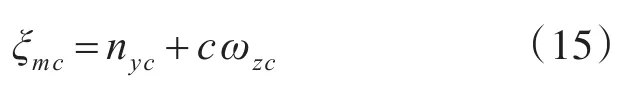
ξm的跟蹤誤差定義為

考慮到系統（7）的相對度為1，選取滑模面為

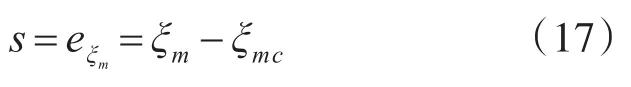
顯然，當系統狀態軌跡到達滑模面時跟蹤誤差也就收斂到零了。對式（17）求導，并將式（7）代入可得

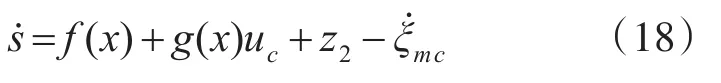
為了使系統狀態軌跡在有限時間內到達滑模面，并且在到達過程中具有良好的動態品質，采用如下的指數趨近律：

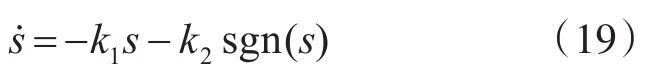
式中：k1＞0，k2＞0，sgn(s)為符號函數。

聯立式（18）和式（19）可以解得

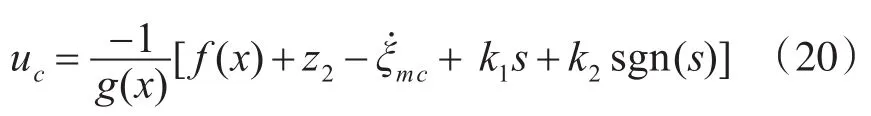
在實際應用中，為了削弱滑模控制的抖振現象，通常對符號函數sgn(s)進行連續化處理，以連續函數替代sgn(s)，其中：ε為一小正數。

4.2 超前動態抗飽和控制器設計

前面設計標準控制器時沒有考慮飽和環節，實際的控制輸入量送入舵機時是受到飽和限制的，由式（3）表示。采用超前動態抗飽和算法來抑制飽和環節的影響，超前激活方式是在原來的飽和環節前面引入一個人為設置的飽和環節，其飽和度低于執行機構的飽和度，以此飽和環節為基礎設計抗飽和補償器。因此，在系統控制輸入達到飽和值之前該抗飽和補償器已經被激活，從而產生抗飽和作用。將超前動態抗飽和補償器加入到標準控制器中，從而構建了超前動態抗飽和控制器。

人為設置的飽和環節的輸出ua為

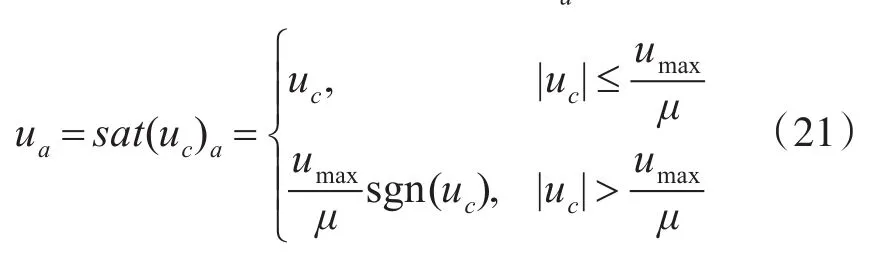
式中：μ＞1；即，人為設置的飽和環節的飽和度小于umax。

超前動態抗飽和補償器設計為

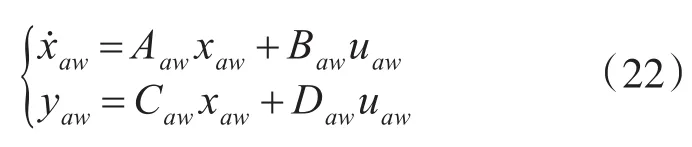
式中：Aaw、Baw、Caw和Daw為抗飽和參數，它們都是常數；uaw為輸入量；yaw為輸出量。

將yaw加入到原來的滑模控制器中，從而構建超前動態抗飽和控制器如下：

5 仿真分析

超聲速反艦導彈在高空飛行時氣動控制效率很低，當過載指令信號突變或者導彈做大機動轉彎時，需要執行機構提供很大的驅動力矩才能完成控制任務。由于存在飽和限制，反艦導彈的實際控制輸入不夠大，與控制器的輸出不一致，進而引起Windup現象。

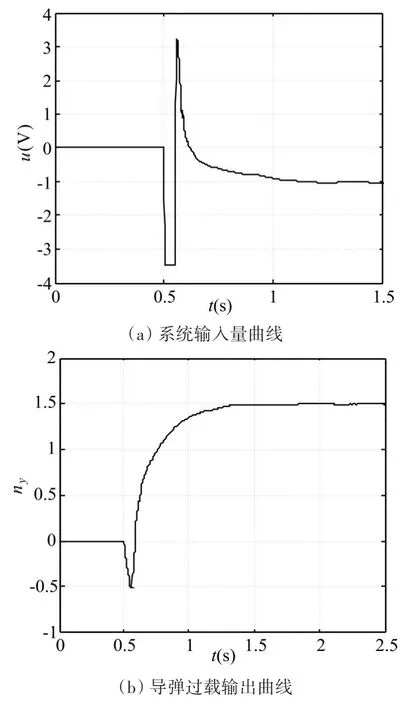
圖1 在特征點1處不加入抗飽和補償器的仿真結果

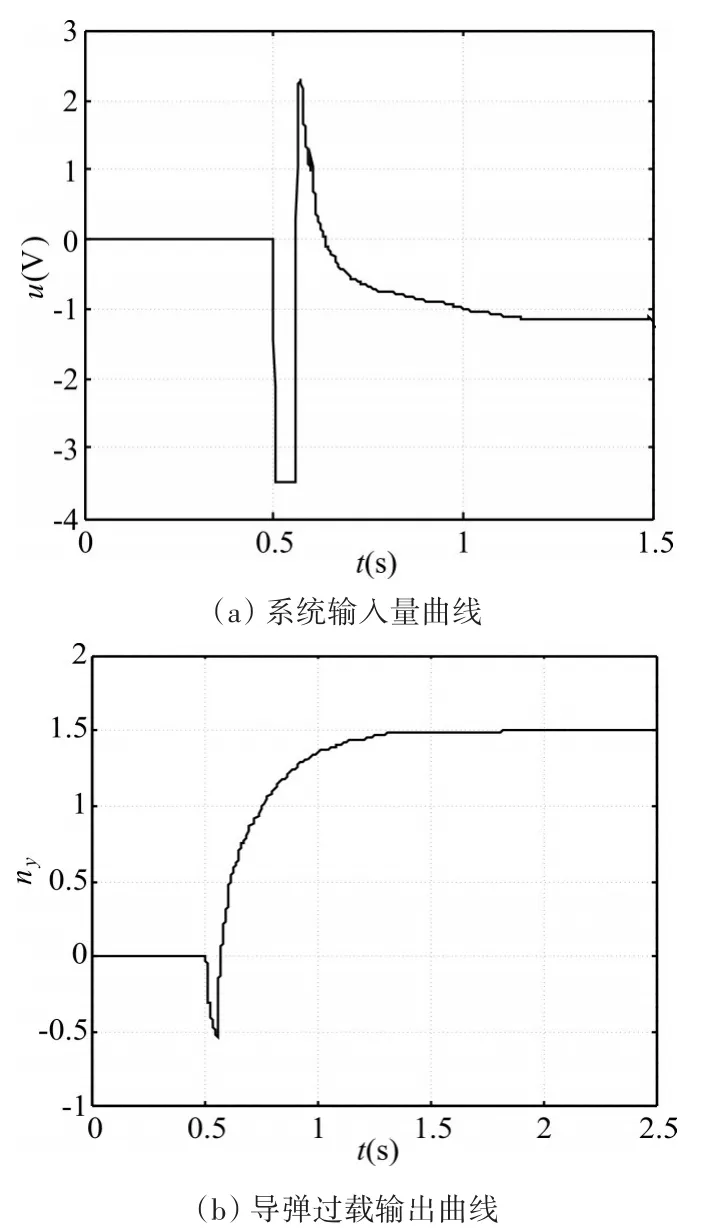
圖2 在特征點2處不加入抗飽和補償器的仿真結果

圖3 在特征點1處加入抗飽和補償器的仿真結果

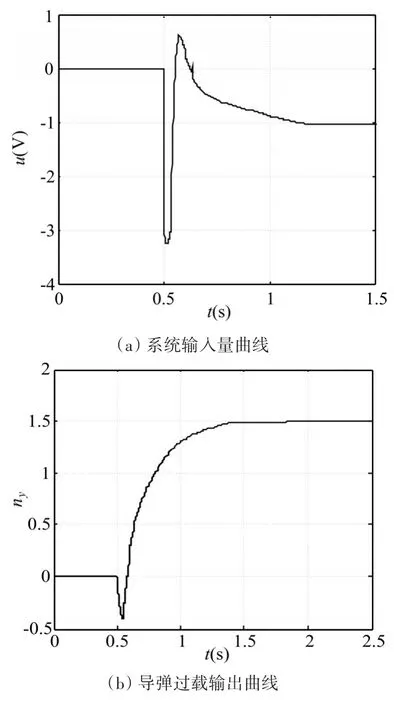
圖4 在特征點2處加入抗飽和補償器的仿真結果

從反艦導彈飛行高度大于14500m的高空彈道上選取2個特征點（編號為1、2）進行仿真分析，并且對不加入和加入超前動態抗飽和補償器兩種情況進行仿真對比。不加入抗飽和補償器時控制器為式（20），加入抗飽和補償器時控制器為式（24）。仿真中，反艦導彈俯仰通道運動模型（1）中的建模誤差假設為周期為0.6s的正弦函數，其幅值（以A(???) 表 示 ） 分 別 為 ：舵機系統的參數為：τ=0.05s，kδ=0.12，送入舵機的電壓最大值為：uδmax=3.5V。選取0.5s啟動的幅值為1.5的階躍信號表示過載指令信號發生了突變。通過仿真調試，確定擴張狀態觀測器的參數為：β01=170，β02=1800，λ=0.5，h=0.04；超前動態抗飽和控制器的參數為：μ=1.2，Aaw=-10，Baw=50，Caw=75，Daw=2.0，k1=30，k2=2.15，c=-78，ε=0.05。不加入抗飽和補償器時，2個特征點處的仿真結果分別如圖1、2所示。加入超前動態抗飽和補償器時，2個特征點處的仿真結果分別如圖3、4所示。

由圖1～圖4的仿真結果對比可知，對于2個特征點而言，在不加入抗飽和補償器時，導彈系統的執行機構都有一段時間處于飽和工作狀態；而加入超前動態抗飽和補償器后，執行機構完全脫離了飽和工作狀態，導彈的過載輸出曲線也基本沒有變化。因此，超前動態抗飽和控制器顯著地減輕了執行機構的工作強度，提高了反艦導彈過載控制系統的控制性能。

6 結語

本文對超聲速反艦導彈的過載控制系統進行了研究。以導彈過載和角速度的線性組合構造組合狀態量，建立了導彈俯仰通道的運動模型。為了對系統中的匯總不確定項進行有效估計，采用擴張狀態觀測器設計了估計器。針對執行機構飽和問題，提出了將超前動態抗飽和算法加入到控制器設計中，即在標準控制器設計的基礎上，加入超前動態抗飽和補償器，綜合起來構成了超前動態抗飽和控制器。從反艦導彈高空彈道上選取2個特征點進行了仿真分析，仿真結果表明，不加入抗飽和補償器時執行機構存在飽和工作狀態；而加入抗飽和補償器時執行機構完全脫離了飽和工作狀態，提高了反艦導彈過載控制系統的控制性能。

參考文獻

［1］Tarbouriech S，Turner M.Anti-windup design：an over?view of some recent advances and open problems［J］.IET Control Theory and Application，2009，3（1）：1-19.

［2］Yang Ming，Niu Li，Xu Dian-Guo.A novel piecewise an?ti-windup design for speed loop PI controller of PMSM ser?vo system［C］//The 14th International Power Electronics and Motion Control Conference，2012：1-4.

［3］李鐘慎，牛彬.一種采用條件技術的抗飽和補償控制器［J］. 華僑大學學報（自然科學版），2011，32（1）：10-12.

［4］Galeani S，Onori S，Teel A R，et al.A magnitude and rate saturation model and its use in the solution of static an?ti-windup problem［J］.Systems&Control Letters，2008，47：1-9.

［5］Song Xiaona，Fu Zhumu，and Liu Leipo.Robust stabiliza?tion of state delayed discrete-time Takagi-Sugeno fuzzy systems with input saturation via an anti-windup fuzzy de?sign［J］.Chinese Physics-B，2012，21（11）：118701：1-118701：8.

［6］Zhao Junjie，Wang Jing，Shen Hao.Dynamic anti-wind?up control design for Markovian jump delayed systems with input saturation［J］.Circuits System Signal Process，2013，32：2213-2229.

［7］ Li Yuanlong，Lin Zongli.Design of saturation-based switching anti-windup gains for the enlargement of the do?main of attraction［J］.IEEE Transactions on Automatic Control，2013，48（7）：1810-1816.

［8］趙紅超，高曉冬，范紹里.基于抗飽和補償的導彈過載控制系統設計［J］. 南京理工大學學報，2012，36（增刊）：154-159

［9］Xianjun Shi，Hongchao Zhao，KewenXu.Dynamic An?ti-windup Design for Missile Overload Control System［J］.Applied Mechanics and Materials， 2012： 236-237，273-277.

［10］Wu Xiongjun，Lin Zongli.Design of multiple anti-wind?up loops for multiple activations［J］.Science China-In?formation Sciences，2012，44（9）：1924-1934.

［11］Wu Xiongjun，Lin Zongli.Dynamic anti-windup design for anticipatory activation：enlargement of the domain of attraction［J］. Science China-Information Sciences，2014，47，012201：1-012201：14.

［12］錢杏芳，林瑞雄，趙亞男.導彈飛行力學［M］.北京：北京理工大學出版社，2012：5-18.

［13］Han Jingqing.From PID to active disturbance rejection control［J］.IEEE Transactions on Industrial Electron?ics，2009，56（3）：900-906.