第二十三講 混料比率設計拾遺
徐靜安
相當長一段時間內,參與討論上海化工研究院內的項目開發,涉及到混料試驗問題。有的項目實驗方案的實施結果較好,有的模型預報、驗證相差甚遠,產生了很大困惑。除了實驗原材料質量控制、實驗誤差外,試驗設計方案的適用性、針對性引起筆者重視。先后精讀了幾本數理統計書中相關章節、案例,此外,還讀了幾本新書,查漏補缺,也避免知識老化。
由何映平編著、化學工業出版社于2013年1月出版的《試驗設計與分析》:該書由化學工業出版社分社杜社長于2014年6月贈送。該書是適用于本科生的基礎教材,側重于正交試驗設計,僅作瀏覽。
由何為、薛衛東、唐斌主編,化學工業出版社于2014年4月出版的《優化試驗設計方法與數據分析》,該書由化學工業出版社分社杜社長于2014年6月贈送。該書是電子科技大學“十二五”規劃研究生教材,常用的正交試驗設計、正交多項式回歸設計、均勻設計、響應曲面試驗設計、三次設計及優選法基礎等作了介紹,數據處理主要是方差分析、回歸分析。該書對工程類研究人員來說有較好的可讀性。
由唐啟義著、科學出版社于2010年2月出版的《DPS數據處理系統——實驗設計、統計分析及數據挖掘》(第2版):該書電子版于蛇年(2013年)由張玉梅贈,紙質版于2014年8月由段敏偉、楊維成、羅勇贈送。該書內容涵蓋廣泛,有1138頁面,仿佛一本統計百科全書,也是以應用為基礎、以DPS軟件功能模塊為支持、涉及實驗數據統計分析和模型模擬方法的工具書。其中,具有全球領先地位的均勻試驗設計、混料試驗設計等幾個功能模塊的獨創算法,對上海化工研究院研究項目具有很高的應用價值,需要精讀。上海化工研究院已購買DPS正版軟件,并在科研一線的10臺計算機上安裝運行。
由關穎男編著、上海科學技術出版社于1990年出版的《混料試驗設計》:該書為筆者查閱到的國內最早出版論述混料試驗設計的專著,多方求購不得,經馬海森、盧浩幫助,于2014年11月19日從網上下載。該書介紹了無附加約束、有附加約束的混料試驗、變量變換及混料數據的分析等。對工程技術人員來說,此書因涉及線性代數等基礎,閱讀難度較大。好在混料試驗設計主體技術已在DPS功能模塊中體現。筆者在瀏覽后對其進行了選擇性閱讀,如混料的比率模型等章節。
在某些混料試驗中,專業知識更關注某些分量百分比之間的相對比率,如混料中2種反應物質的比例對收率的影響等,其中x1價格較貴,x2價格便宜,且過量的x2容易從產物中分離。研究的興趣在于考察x2/x1對響應Y的影響。
此外,在P因素混料試驗中,由于∑xi=1,其中每個因素變化都不是獨立的。如果將P個因素,分量的百分比化成P-1個比率,則每一個比率能獨立變化。
從筆者所見案例:如 P=3,x1,x2,x3可化成 x1/x2,x2/x3,也可化成 x1/x2+x3,x2/x3;對 P=4,x1,x2,x3,x4可化成x1/x2,x1/x3,x1/(x3+x4);對P=5,x1,x2,x3,x4,x5可化成x2/x1,x2/x3,x1/x4,x5/x3等。
在(P-1)個比率中,似無定規,只要求每一個比率中至少有一個自然因素xi與其他的比率聯系起來。比率的組合形成及選定的考察水平,可根據專業知識來確定,有較大的靈活性。
一、案例
利用混料的比率設計研究白色陶器組分與其吸水性之間的關系。需考察的因素是4個成分:霞石正長巖(x1),長石(x2),黏土(x3)與燧石(x4)。
選L8(27)正交表,因素水平及編碼如表1、表2所示,擬采用一次回歸正交試驗設計。

表1 因素(比率)水平表
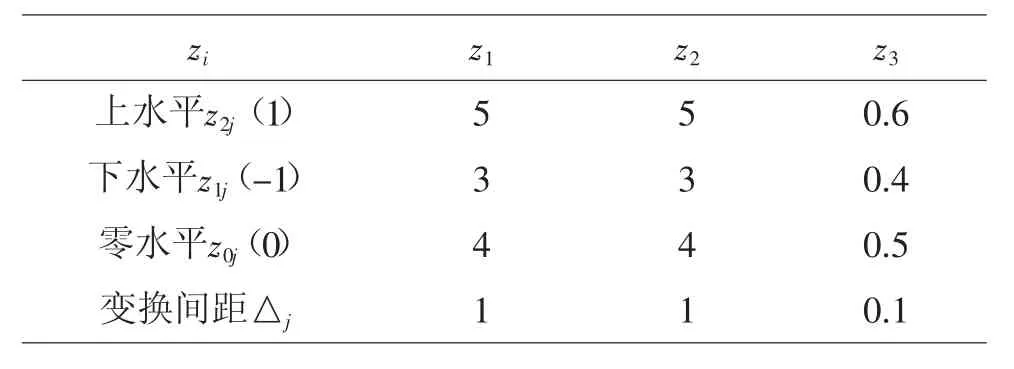
表2 因素水平編碼表
由此在正交試驗L8(27)表上形成一次回歸正交設計編碼表及相應實驗結果(見表3)。
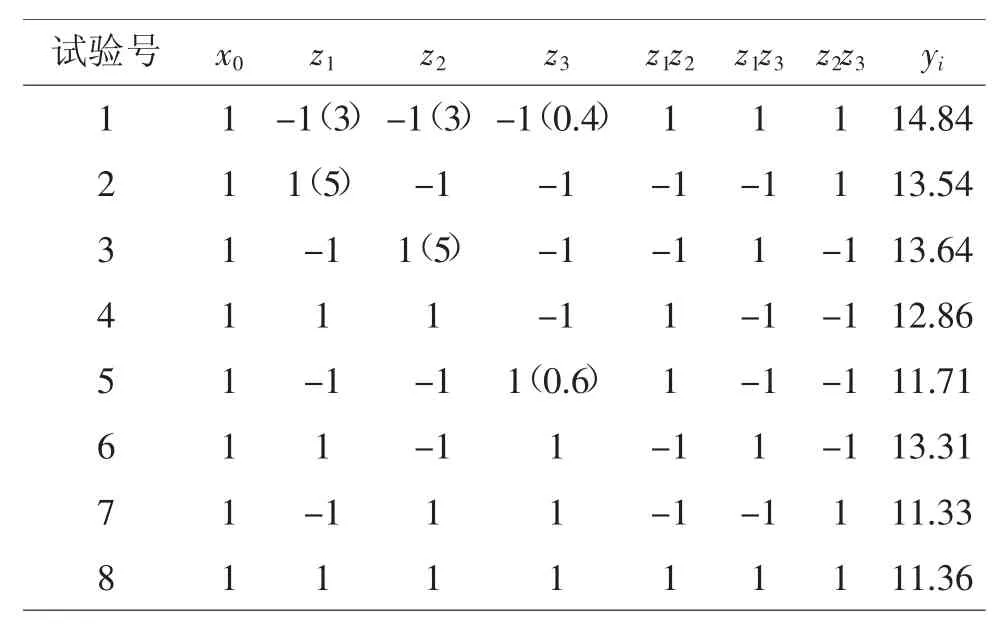
表3 一次回歸正交設計編碼表及相應實驗結果
在實際實驗時,需要把每一號試驗的比率組合換算成自然因素的百分比組合。如以x2為基礎,對第1號試驗:由z1=x1/x2=3,得x1=3x2;由z3=x3/(x1+x2)=0.4,得 x3=0.4(3x2+x2)=1.6x2;由 z2=x3/x4=3,得 x4=x3/3=1.6x2/3=0.533x2。
由此可得:
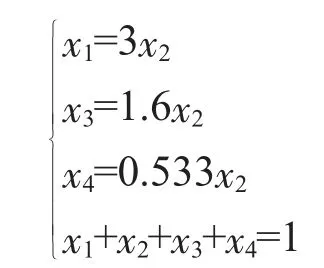
對P個自然分量百分比,化成P-1的混料比率,再加約束∑xi=1,方程組可解。可解得:x1=48.92%,x2=16.31%,x3=26.09%,x4=8.69%。
以此類推,可得各試驗號的百分比組合。由此可得各分量實驗范圍的上、下限。x1:41.67%~56.31%;x2:9.26%~16.89%;x3:26.09%~34.88%;x4:5.41%~11.11%。如果對某個分量考察范圍不認可,則需調整對應混料比率的水平值。這是混料試驗的本質所在,應重視。因素百分比組合試驗方案見表4。
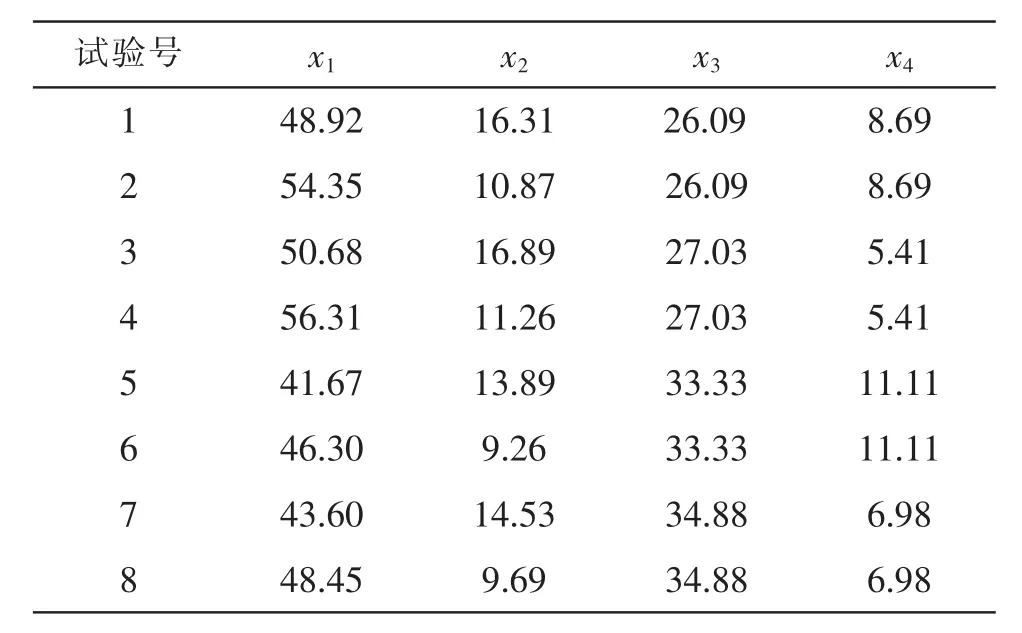
表4 因素百分比組合試驗方案表
本文重點不在于介紹一次回歸正交設計的計算過程,該類試驗設計于20世紀70年代中后期開始推廣應用,目前在計算機軟件的支持下,已有了更高級的試驗設計。有興趣的讀者可查閱相關著作。
經中心化轉換可得全回歸方程:
Y=12.824-0.056z1-0.526z2-0.896z3-0.131z1z2+0.464z1z3+0.05z2z3。
二、討論
1.對于正交設計、組合設計等也要求變量獨立,案例采用混料比率設計,在一次回歸正交設計中成功應用,并建立相應的統計模型,用混料比率可以解除混料自然組分百分比變化時的隱性混雜,混料比率變化獨立。
2.在確定的P-1個比率中,要求每一個比率中至少有一個自然因素與其他的比率聯系起來,從而可解得每個試驗號各組分的自然百分比組合。這是混料比率設計的技術核心。
3.根據專業知識選定混料的比率形式及變化的范圍,文中因素(比率)水平表體現了比率形成及考察變化的范圍。
4.當混料中根據專業知識選定混料比率的同時,如果各分量兼受專業上的上、下限約束時,問題比較復雜,相關著作沒有展開討論。
筆者建議:
(1)首先按本刊2018年第一期刊登的第二十一講“混料配方研究中極端頂點設計的應用解讀”中,對各分量的上、下限約束進行檢查,解除多余約束:
有上下限約束的混料試驗:
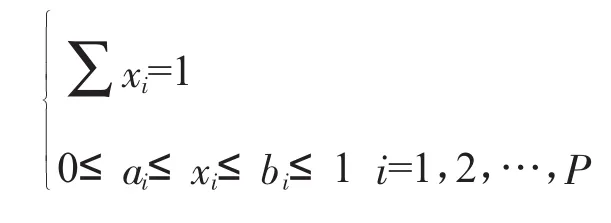
經計算,a=∑ai<1,b=∑bi>1。
令 ai=max(ai,bi+1-b),bi=min(bi,ai+1-a),新得到的ai,bi排除了多余的約束。
(2)根據混料比率及考察變化范圍選擇試驗設計方案,如案例選用一次回歸正交設計,對每個試驗號的比率組合計算自然因素的百分比,由表可見每個自然因素,即分量的上、下限。
(3)由(1)解除多余約束所得分量上下限;由(2)混料比率結合具體試驗設計的試驗號計算各分量百分比組合所得分量上、下限,二者可能不一致。此時在確保“鋼性”約束外,可以調整混料比率水平的變化,也就是要“試湊”混料比率,使由(2)計算的上、下限值接近及處于由(1)計算所得上、下限的范圍內。
5.混料比率設計及下述的有過程參數的混料比率組合設計,在工程界獲得應用。但是,上述的“試湊”過程,由于混料比率形式的靈活性,過程計算、調整比率值等比較繁瑣,沒有得到MINITAB、DPS等軟件相應模塊的支持,需要應用者自行計算完成。由于“試湊”過程繁瑣,教材類的數理統計專著也不作為混料試驗設計的主流技術加以討論。工程界應用混料比率設計的主要原因是專業需要以及設計方案形成不需要過多數理統計知識支持,簡單、直觀,尤其是可進行傳統的單因素探索性考察實驗。
6.由于混料比率設計中變量獨立,可用于一次回歸正交試驗設計,采用全回歸建模。進一步引伸,也可用于均勻設計,形成混料比率均勻設計,采用逐步回歸建模。
如果按原案例的混料比率及考察范圍,選用表及其使用表具體見表 5、表 6。在1,3,4 列安排 z1,z2,z3。z1,z2的 8 個水平分別為3.0,3.3,3.6,3.9,4.2,4.5,4.8,5.0;z3的 8 個 水 平為0.40,0.43,0.46,0.49,0.52,0.55,0.58,0.60。由此,在(85)均勻表上形成混料比率均勻設計,具體見表7。
在實際實驗時,仍需把每一號試驗的比率組合換算成自然因素的百分比組合。也以x2為基礎進行上述的計算,可得試驗號的百分比組合。
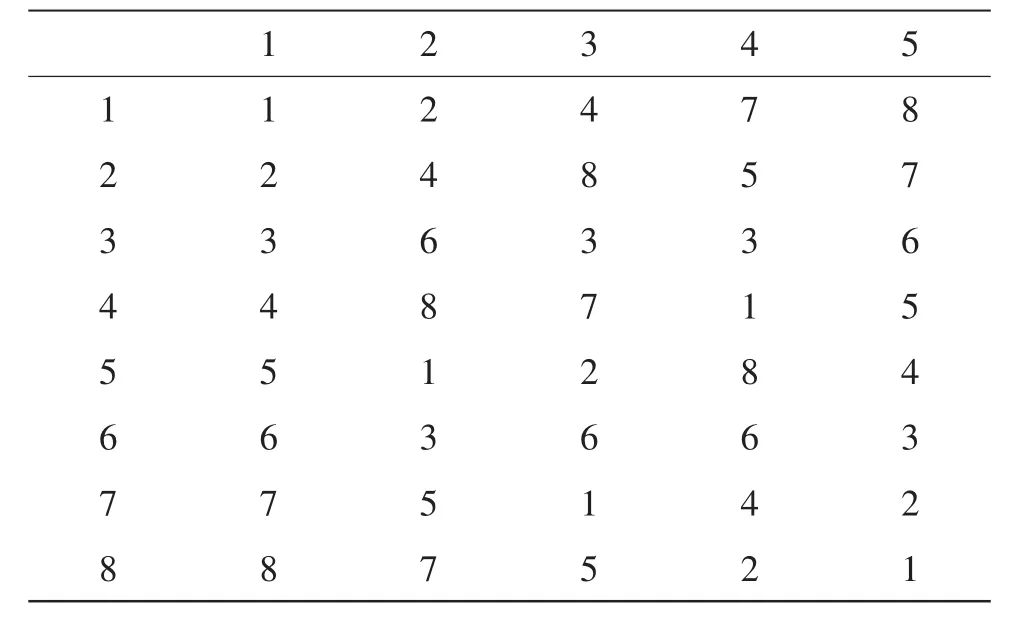
表5 U8*(85)表
表6 (85)的使用表

表6 (85)的使用表
因素數 列號 D 2 1 3 0.144 5 3 1 3 4 0.200 0 4 1 2 3 5 0.270 9
表7 (85)的混料比率均勻設計
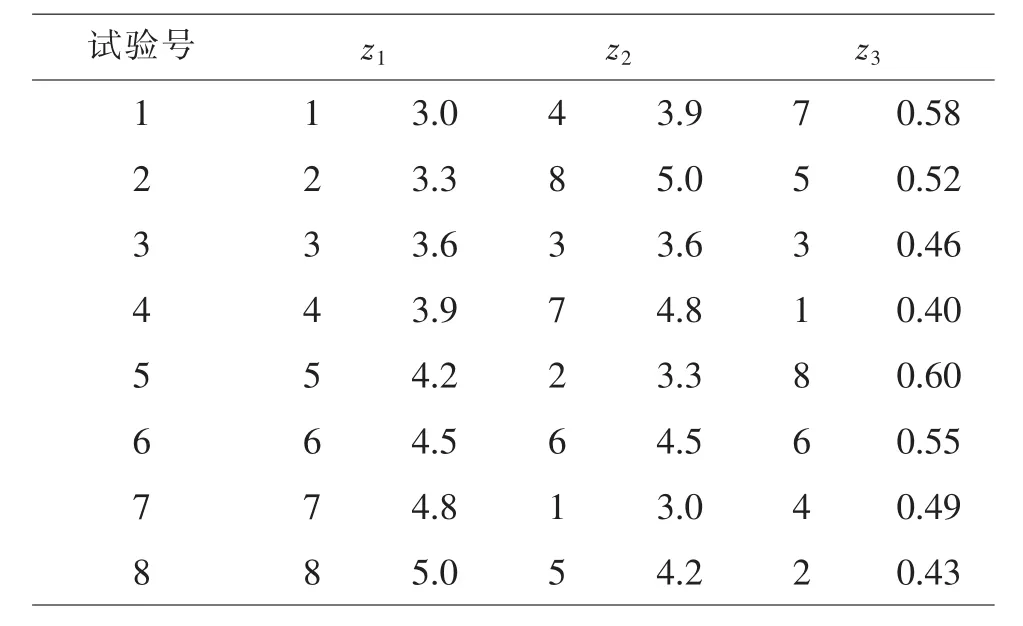
表7 (85)的混料比率均勻設計
試驗號 z1 z2 z3 1 1 3.0 4 3.9 7 0.58 2 2 3.3 8 5.0 5 0.52 3 3 3.6 3 3.6 3 0.46 4 4 3.9 7 4.8 1 0.40 5 5 4.2 2 3.3 8 0.60 6 6 4.5 6 4.5 6 0.55 7 7 4.8 1 3.0 4 0.49 8 8 5.0 5 4.2 2 0.43
顯然,采用表安排混料比率的優勢在于實驗方案的均勻性,zi多水平統計建模的模型穩定性。
7.進一步引伸,在同時考察工藝參數溫度、時間、壓力等影響的混料試驗問題中,按上述討論先將混料試驗問題轉化為混料比率試驗問題,再組合工藝變量,選擇均勻設計表,構筑成混料比率組合均勻設計。
有限的著作例舉了相同的案例,如進行某合金的強度試驗,要考察合金的混料組分鐵(x1)、鎳(x2)、碳(x3)和鉻(x4),同時考察工藝因素,退火溫度、退火時間。這是一個四分量混料問題,轉化為P-1=4-1=3的混料比率:z1=x1/x2,z2=x1/x3,z3=x1/(x3+x4),組合兩個工藝因素,z4'=退火溫度,z5'=退火時間,按5個獨立變量選擇均勻設計表。
混料比率組合均勻設計在工程性技術開發中很有應用前景。本刊2017年第四期刊登的第十二講“均勻設計實驗方案選擇的幾點考慮”中,列舉了“均勻設計法在三鄰苯二胺基環三磷腈合成中的應用”。在親核取代反應中考察:反應時間x1=8.0~24.0 h、原料配比 x2n(鄰苯二胺)∶n(六氯環三磷腈)=2.9~4.5、縛酸劑用量x3n(三乙胺)∶n(六氯環三磷腈)=5.5~7.5。混料比率設計中,用自然分量六氯環三磷腈把P-1=3-1=2個混料比率聯系起來,作為獨立變量就能構筑成混料比率組合均勻設計。見表8。
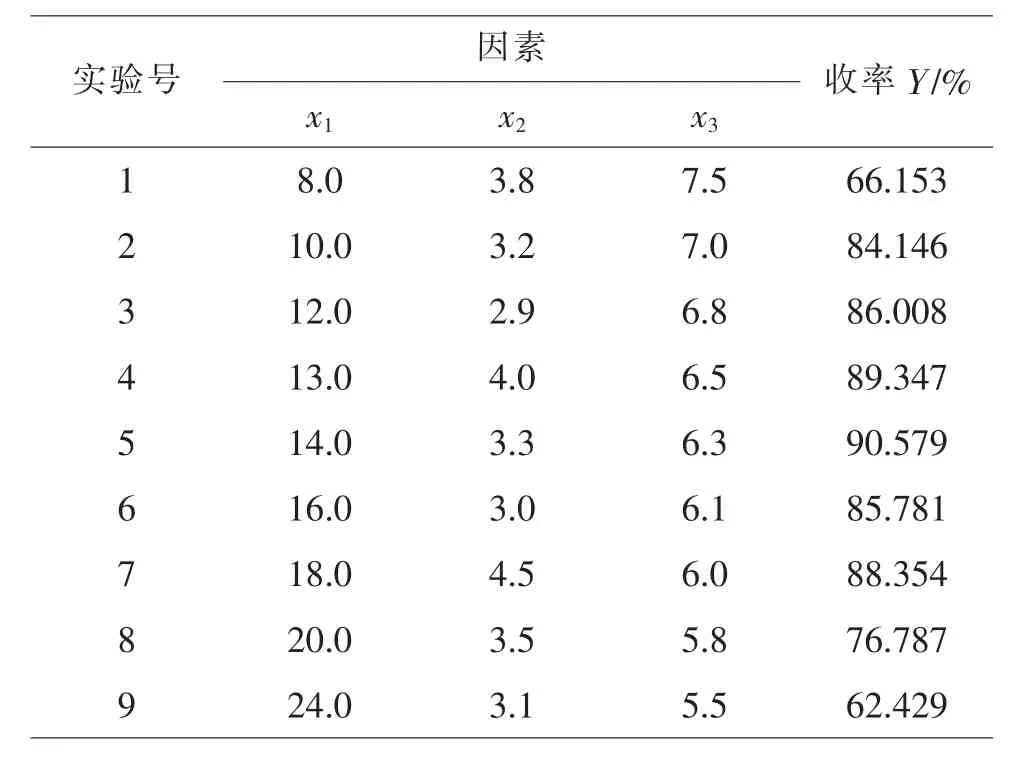
表8 均勻設計實驗方案及結果表
用三元二次多項式逐步回歸建模:
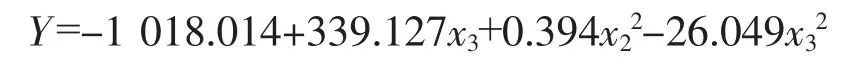
回歸方程 R=0.99,S=1.72,P=0.000 1,F=94.96>F0.05(3,5)=5.41回歸方程具有顯著的統計意義。DPS軟件預測考察范圍內反應最佳條件為x1=14.57,x2=4.5,x3=6.5,Y=93.73。x1反應時間不顯著,為考察范圍內隨機值。三次驗證實驗穩定,擬合、預報功能良好。見表9。

表9 最佳條件驗證實驗表
顯然,這樣構筑的混料試驗方案,不僅比傳統單配方考察減少了實驗工作量,且能規范地建立、檢驗統計模型,避免隱性混雜,充分挖掘實驗數據信息,穩定地預報優化工藝加配方組合,值得探索應用。
三、補缺
在工程性研究中,往往對混料中某2個主成分間的比率更為關注,在單因素探索試驗階段,在考察工藝因素的同時,也對主成分比率進行考察,而暫不對混料進行全面考察;還有的采用混料多重比率(x1∶x2∶x3)組合工藝因素進行考察。相關著作均未涉及此類混料比率問題展開討論。
1 主成分混料比率考察
設定研究對象是P=4混料試驗,以重量克(g)為計量單位。起始混料配方為:x14.89 g,x21.63 g,x32.61 g,x40.87 g。現對混料比率單項考察z=x1/x2=3~5。在單因素考察時,要求相關因素固定不變。
當z變化到Z=x1/x2=5時,混料配方為:x18.15 g,x21.63 g,x32.61 g,x40.87 g。此時,z=5,x2,x3,x4的絕對量未變化;但是,x2,x3與x4的組分百分比有了變化,產生隱性混雜。見表10。
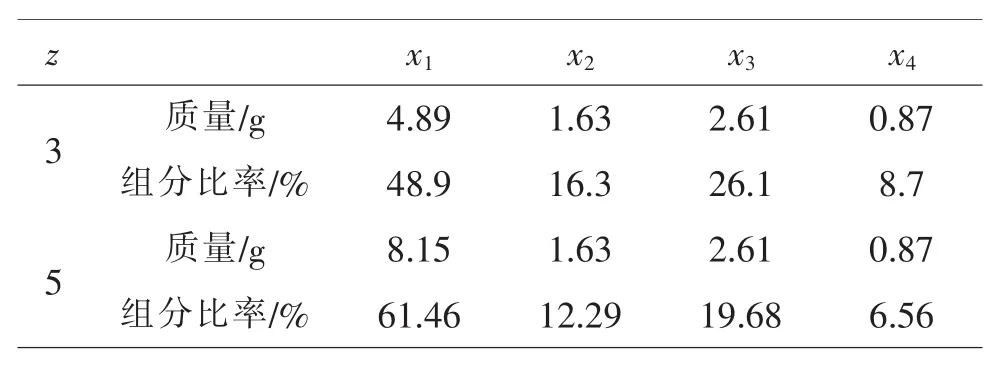
表10 混料比率考察
如果采用本講義前述的方法,即使在單比率考察時,也對混料比率作整體設計,采用組分百分比的比率。如前述轉化為P-1=4-1=3個混料比率:z1=x1/x2,z2=x3/x4,z3=x3/(x1+x2),把起始混料組分代入得z1=3,z2=3,z3=0.4。固定 z2,z3,考察 z1單比率變化對 Y的影響,z1=3~5,用前述的方程組,可得自然組分xi的百分比,x3,x4組分百分比固定。具體見表11。
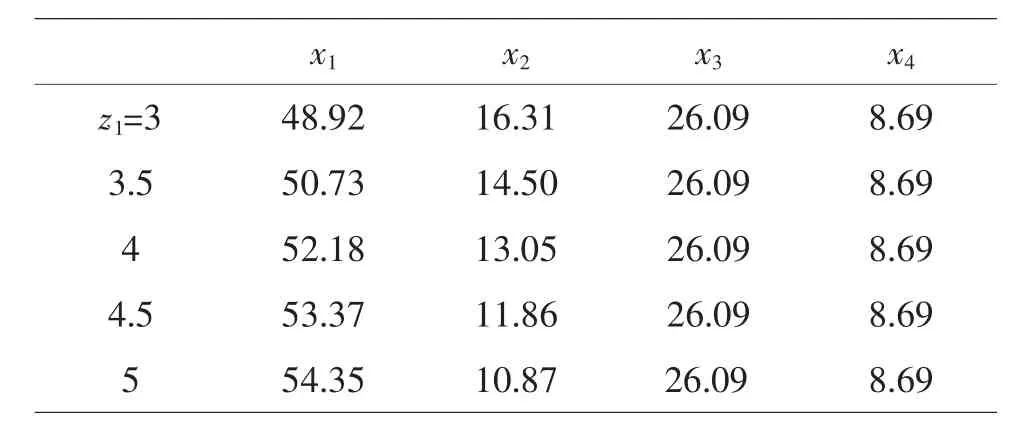
表11 混料比率考察結果
質疑是創造性思維模式之一。科學強調批判性,沒有質疑、批判就不知前人理論、知識、技術的不足和缺點。當然,也包括自己對過去認識的反思,質疑、批判是為了往前走,是為了技術進步,不是為了批判而批判,也不是無依據地質疑,所以還要在學習基礎上提出建設性方案,再通過實踐加以驗證。
筆者對上述混料主成分比率兩種方法的差異進行展開、初步的計算分析。這兩種方法在工程界易混淆,相關著作未見討論,而研究報告應用效果也似是而非,主要是缺乏驗證性實驗結果。筆者從混料試驗的本質內涵是xi組分百分比在對響應值Y起作用,以及數理統計單形坐標系中∑xi=1的約束考慮,組分百分比的比率獨立,似乎更為合理。愿和同仁們進一步討論。
2 多重混料比率組合試驗
在工程性混料試驗時,對P=3的混料問題,常見直接采用多重比率作為一個綜合變量和工藝參數組合進行試驗設計。
如在Ni-5%合金基帶電化學拋光工藝的初步探索時,根據文獻及專業經驗初定考察范圍,選擇表,實驗結果見表12。

表12 多重混料比率組合試驗結果
表中電解液配比為:正磷酸∶濃硫酸∶有機添加劑的多重比率。該多重比率采用體積比為V1∶V2∶V3,且∑Vi=10。
初步探索試驗,要求基帶表面粗糙度Rms≤10 nm,直觀分析No3與No6為好點,6次實驗考察P=3的三組分混料配方并組合3個工藝參數而獲得好點,實驗效率很高。如果要求獲得統計模型,求取優化的工藝條件,可把多重比率綜合看作為一個定性變量,即配方1、配方2、……、配方6。在統計建模時定義為偽變量(有,無)對應二進制的(1,0)。
僅限筆者所見,在混料試驗領域個別專著引用的案例、一些公開發表的科技論文、院內的某些研究報告,其中出現似是而非的結果,以及預報和驗證值相差甚遠、乃至離譜結果的案例,大都涉及試驗設計方案中混料組分變量的不獨立性,因產生隱性混雜而造成,應予以重視。
后記:
2013級研究生編寫開題報告期間,彭東輝、吳向陽教授及李志剛導師助理帶教的浦靜雯碩士的研究生課題涉及混料試驗設計,我應邀多次參與該課題討論,結合院內項目,趕寫此文,浦靜雯積極學習并打印。

