基于近似l0范數的稀疏信號重構

聶棟棟 弓耀玲

(燕山大學理學院 河北秦皇島 066004) (niedd@ysu.edu.cn)

自壓縮感知(compressed sensing, CS)信號處理理論[1]提出以來，信號重構作為其關鍵的環節，一直是該理論的研究重點.信號重構的目標是根據非自適應線性測量的低維數據，準確而有效地恢復原始采樣獲取的高維數據.在壓縮感知理論框架下，信號在特定基下或一定的變換下可稀疏表示，則信號重構問題可轉化為稀疏信號的重構.如何求欠定方程組最稀疏的解是稀疏重構問題的本質，即l0范數的最小化問題.

然而直接求解欠定方程組的最稀疏解是NP難問題，處理起來非常棘手.在實際中，貪婪算法是最常見的近似求解方法[2-5]，如正交匹配追蹤法(orthogonal matching pursuit, OMP)[2]、梯度追蹤法(gradient pursuit, GP)[3]、子空間追蹤法(subspace pursuit, SP)[4]等，其基本思想是通過逐步迭代找到未知信號的支撐集，原信號的估計值即可利用最小二乘法得到.貪婪類算法需要較少的計算量，但是通常估計精度不高且需要較多的觀測值.

另一種思路是尋找新的模型替代l0范數的求解.這種方法分為2步：

1) 需要找到合適的函數近似估計l0范數，由于l0范數是x的不連續函數，實際計算中不好處理，很多文獻常用l1范數來近似l0范數，如基追蹤法(basis pursuit, BP)[6]，其依據是l1范數最小化與l0范數最小化在滿足一定條件時具有相同的稀疏解，可以通過線性規劃方法求解.然而，l1范數不能充分反映向量x的稀疏特性，重構時需要較多的測量值，計算量較大.高斯函數類也是近似l0范數經典的函數之一，基于光滑l0范數算法(smoothedl0norm, SL0)[7]是用一個連續平滑函數的極限來近似l0范數，如文獻[7-8]采用

(1)

對l0范數進行近似，其中σ為趨于0的正數.文獻[9-10]則在式(1)的基礎上進一步改進，采用式雙曲正切函數

(2)

近似l0范數，其中σ為很小的正數.在文獻[11-13]中，用一組反正切函數

(3)

近似l0范數，其中σ為接近于0的正常數.文獻[14]是采用復合三角函數近似l0范數.但以上函數表達式均稍復雜，使得迭代計算復雜度較高.文獻[15]的快速稀疏信號恢復算法(AL0算法)提出用函數

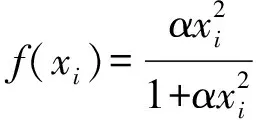
(4)

2) 對新的函數模型選擇不同的線性規劃或優化算法求解.對于算法實現，NSL0算法選用修正牛頓法求解最優化問題，需要對海森矩陣進行修正，構造一個可近似海森矩陣逆的正定對稱陣作為迭代方向，一定程度上提高了收斂速度.AL0算法將問題分解為2個最小化問題分別求解，然后交替迭代，將解投影到可行域.本文選取高精度的牛頓迭代法，將問題轉為無約束優化問題后，對無約束問題直接應用牛頓算法，迭代得到最優解，不需要進一步對解進行投影.而且得到的牛頓方向為下降方向，不需要進一步修正，從而減少了誤差影響，保證了精度.

信號的恢復質量在算法的不斷改進下有所提升，但仍存在存儲量大、計算復雜度高、精確度不夠高等問題，需要進一步研究和改進.本文在之前l0范數工作的基礎上，結合AL0算法快速收斂和牛頓迭代法高精度的優點，提出新的基于近似l0范數的稀疏信號重構算法，用一個簡單的分式函數的和來近似估計l0范數，通過牛頓迭代算法求得稀疏解.最后，通過數值仿真和已有的相似算法及經典的OMP算法進行比較，并分析了本文算法恢復的信號在重構誤差、信噪比方面的優勢.

1 壓縮感知理論

令z∈n是傳統采樣得到的信號，經過正交基或緊框架ψ變換后的系數是稀疏的，即z=ψx，其中x∈n且為稀疏度.在無噪聲干擾的情形下，測量向量y可以表示為y=Φψx，其中y∈m，Φ為m×n維測量矩陣，ψ為n×n維基矩陣.令A=Φψ，則重構問題簡化為在矩陣A和測量向量y已知的條件下，求方程組y=Ax最稀疏解的問題，即l0范數的最小化問題：

(5)

在實際應用中往往會不可避免地受噪聲的影響，測量值是不精確的，令γ表示噪聲，則測量值進一步表示為y=Ax+γ.

2 基于近似l0范數的稀疏信號重構

2.1 l0范數近似

本文采用一個形式較為簡單的分式函數

(6)

來近似l0范數，其中δ是很小的正數，實驗中參數δ可取為一組下降且趨于0的序列.顯然有:

(7)

令:

(8)

根據l0范數的定義可知，當δ無限趨近于0時，F(x)的值就無限接近于向量x中非0元的個數，即x的l0范數，故有:

(9)

因此,我們可以用式(8)來近似l0范數進行迭代計算.式(6)的優勢在于形式簡單，尤其在算法迭代時簡化了計算，同時又不降低精度.

2.2 算法實現

本文將最優化問題式(5)等價變換為拉格朗日形式最小化問題：

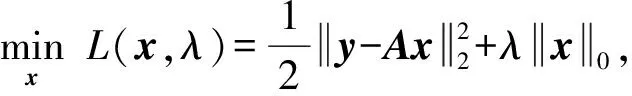
(10)

其中,λ是拉格朗日乘子.然后對式(10)進行求解.由2.1節可知，式(10)可轉化為

(11)

式(11)是無約束的最優化問題，最優解x*滿足優化條件:

(12)

進一步有:

(13)

其中,f′(x)為f(x)的導數，AT為A的轉置.

當δ→0，

(14)

為方便表示，令:

(15)

Hf=ATA+λXf,

(16)

(17)

由式(17)可以得到Hessian矩陣可表示為

(18)

顯然，Hessian矩陣Hf為正定矩陣，故得到的牛頓方向必然為下降方向，可以利用牛頓迭代[16]求解式(11)得：

(19)

式(19)即算法的迭代式，hx為迭代步長，初始解x0取最小二乘解.

鑒于求逆運算會隨著矩陣維數的增高計算量迅速加大，為盡量降低算法的計算復雜度，考慮在算法迭代中設法降低維數.

由于稀疏化后的信號向量的大部分值為0或接近于0，故可以只迭代計算對應變量的關鍵元素，如變量中絕對值最大的l個分量，忽略0元素及接近于0的元素.

令：

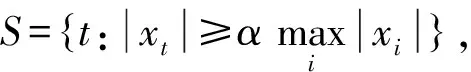
(20)

其中，參數α∈[0,1)，通常可取α=0.01.

xS=(xi),i∈S,

(21)

AS=(ai),i∈S,

(22)

其中，ai為A的第i列，則算法迭代的Hf可替換為

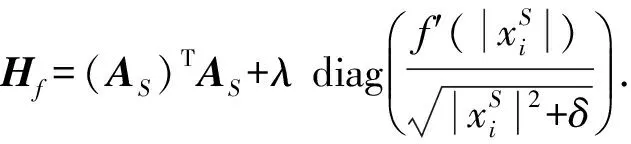
(23)

相應地:

(24)

2.3 算法的計算復雜度分析

在算法實現過程中，直接計算式(19)時，涉及到矩陣和向量的乘積及矩陣的求逆，假設A是n×n矩陣，y為n×1向量，則ATy的計算復雜度為O(n2)，對Hf求逆的計算復雜度為O(n3).

經過降維后，令l為式(20)中S的元素個數，則如式(23)，對Hf求逆的計算復雜度變為O(l3)，而通常情況下，l?n，從而使得本文算法每次迭代的計算復雜度維持在O(n2)，這與SL0，NSL0，OMP，AL0算法的計算復雜度均是相當的.

2.4 算法描述

本文算法的偽代碼描述如下：

算法1. 基于近似l0范數的稀疏信號重構算法.

輸入：矩陣A、測量向量y、正則化參數λ、參數δ、終止條件δmin；

輸出：重構信號x.

初始化：初始解x0=AT(AAT)-1y.

迭代：

步驟1. 令:

S={t:|xt|>0},
xS=(xi),i∈S,
AS=(ai),i∈S;

步驟2. 更新矩陣：

步驟3. 迭代x，

步驟4. 更新δ，δ=δ×0.5；

步驟5. 判斷算法是否終止，若δ>δmin不滿足輸出迭代的結果x，否則返回步驟1繼續迭代.

2.5 算法的理論證明

在不考慮噪聲存在的情況下，算法的理論證明如下.

證明. 由矩陣逆的分塊形式知：

(25)

(26)

將式(25)帶入式(26)并經過推導可以得到:

證畢.

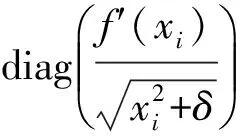
(ATA+λXf)-1ATy=x.

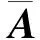
(27)

(28)

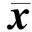
證畢.

3 仿真實驗

為驗證本文算法的有效性，對一維隨機稀疏信號進行實驗，并與經典算法OMP及相似的AL0算法等進行了比較.下面所有數值仿真中，矩陣A取高斯隨機矩陣, 測量值向量通過y=Ax+γ生成, 其中γ表示高斯白噪聲.實驗采用信噪比(signal noise radio,SNR)作為評估算法精度的性能指標，定義為

(29)

其中,xopt表示對源信號x的稀疏估計值.相對誤差定義為

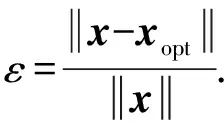
(30)

實驗中隨機產生稀疏信號x和矩陣A，實驗結果在參數設定的情況下進行100次求平均.實驗條件為ThinkpadT410i筆記本電腦Microsoft Windows 7操作系統MatlabR2010a 處理平臺的運行環境.

實驗1. 測試不同算法的整體恢復性能.在相同取值下，信號長度n=256，稀疏度k=20，測量值向量長度m=128，噪聲均方差取為0.01，分別測試本文算法(Proposed)、AL0算法、SL0算法、NSL0算法及OMP算法所重建的信號在信噪比、重構誤差和重構時間方面的對比.結果如表1所示，可以看出，本文算法重建的信號信噪比提升幅度較大，相對誤差也較低，較優于其他算法.

Table 1 Performance Comparison under Different Algorithms表1 各算法恢復性能比較

實驗2. 測試在不同數量測量值的情況下，各算法的性能.信號長度n=256，稀疏度k=20，測量值數量分別是100，128，150，192時，測試各算法的恢復效果.結果如圖1～3所示.

圖1是信噪比隨測量值數量的變化曲線圖.測試結果表明：在不同壓縮比下，本文算法所重建信號的信噪比均高于對比算法，信號的精確度有較大的提升.

圖2是相對誤差隨測量值數量變化的曲線圖.由圖2可以看出，在壓縮比較低時，各算法的重建誤差都比較大，但是隨著測量值數量的增加，本文算法重建信號的相對誤差比其他算法都有所降低，優勢進一步體現.

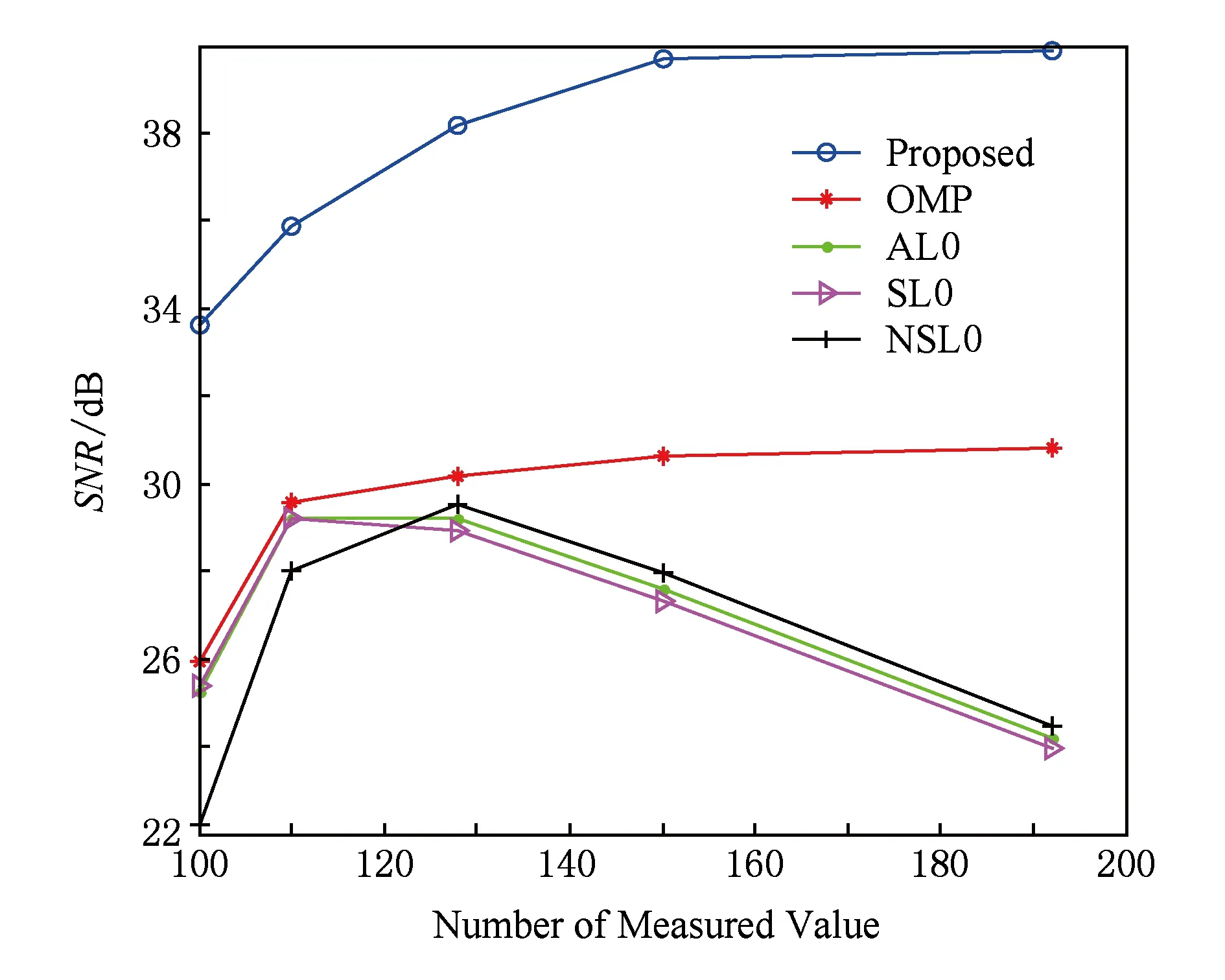
Fig. 1 SNR comparison under different number of measured value圖1 不同測量數值各算法重構信號的信噪比

Fig. 2 Relative error comparison under different number of measured value圖2 不同測量數值各算法重構信號的相對誤差

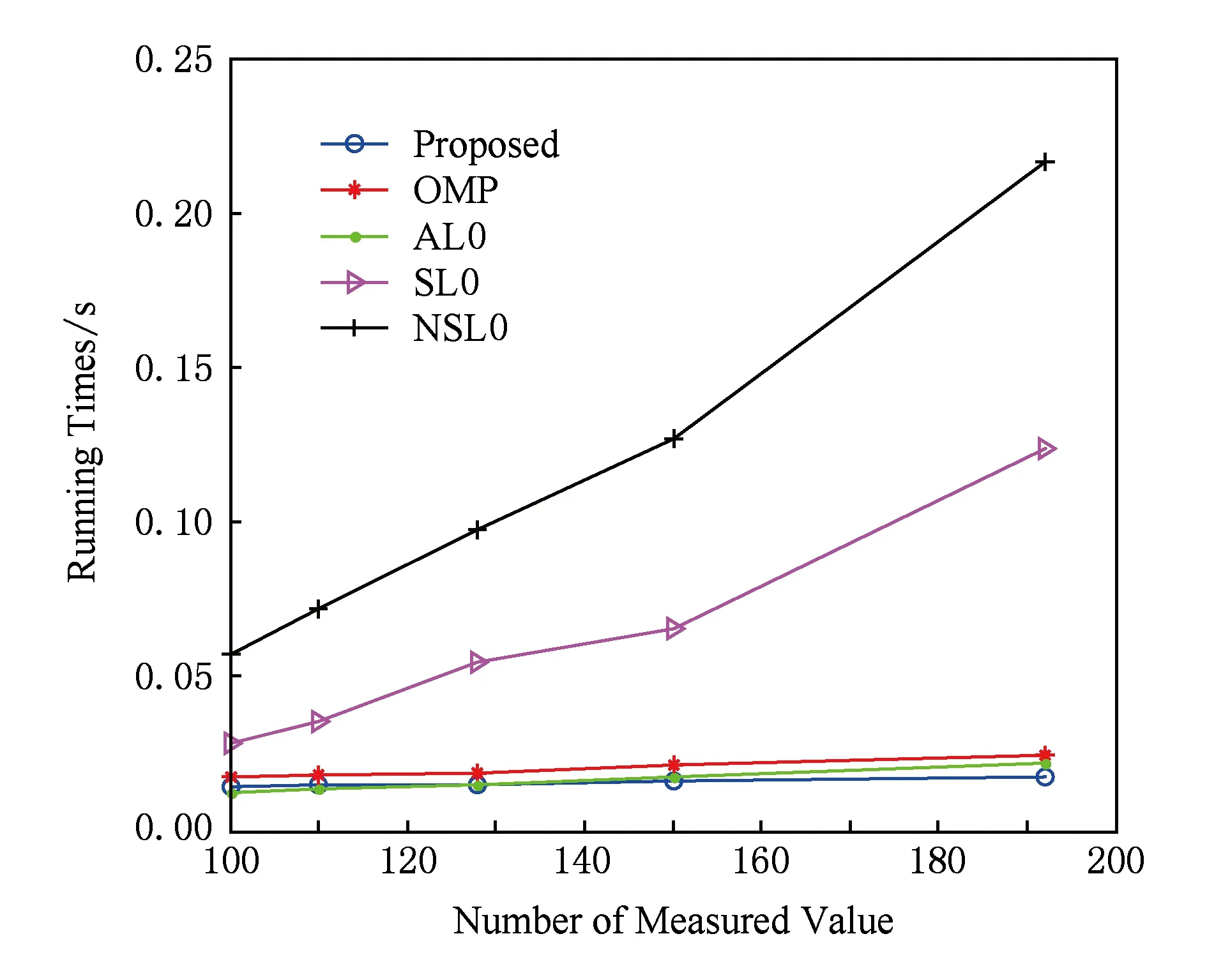
Fig. 3 Time comparison under different number of measured value圖3 不同測量數值各算法重構時間

圖3則展示了各算法的重構時間，在各壓縮比下，本文算法的運算時間要少于NSL0算法和SL0算法，和AL0算法相差不大.實驗3. 測試算法在不同稀疏度情況下的恢復精度.信號長度n=256，壓縮比m/n=0.5，稀疏度由15～35變化，分別測試各算法的恢復效果.結果如圖4所示，仿真結果表明：在不同稀疏度下，由本文算法所重建信號的信噪比均高于對比算法，尤其在稀疏度較低時，本文算法恢復的信號精度提高較大.

Fig. 4 SNR comparison under different sparseness圖4 不同稀疏度下各算法重構信號的信噪比

實驗4. 測試算法在不同噪聲水平下的恢復精度.信號長度n=256，壓縮比m/n=0.5，噪聲均方差由0.004～0.02變化，分別測試各算法的恢復效果,結果如圖5所示.可以看出，在不同噪聲水平下，與對比算法相比，本文算法依然保持優越性，重建信號的信噪比仍提高較大.進一步說明在噪聲干擾較小時，本文算法的性能要較好.

Fig. 5 SNR comparison under different noise levers圖5 不同噪聲均方差下各算法重構信號的信噪比

4 總 結

本文在之前l0范數工作的基礎上，結合AL0算法快速收斂和牛頓迭代法高精度的優點，用一個簡單的分式函數的和來近似估計l0范數，通過牛頓迭代算法求得稀疏解，從而對AL0算法恢復信號的精度不夠高的缺陷得以改進.最后通過數值仿真，在恢復精度上和經典的OMP算法、相似的現有算法進行了比較.數值仿真結果表明：在不同壓縮比、稀疏度及噪聲干擾下，本文算法恢復精度均有較大提升，有效地改善了重建效果，提高了信號的重建質量.

[1]Candes E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30

[2]Tropp J A, Gilbert A C. Signal recover from random measurements via orthogonal matching pursuit[J]. IEEE Trans Information Theory, 2007, 53(12): 4655-4666

[3]Blumensath T, Davies M E. Gradient pursuits[J]. IEEE Trans on Signal Processing, 2008, 56(6): 2370-2382

[4]Dai Wei, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Trans Information Theory, 2009, 55(5): 2230-2249

[5]Pei Tingrui, Yang Shu, Li Zhetao, et al. Detouring matching pursuit algorithm in compressed sensing[J]. Journal of Computer Research and Development, 2014, 51(9): 2101-2107 (in Chinese)

(裴廷睿, 楊術, 李哲濤, 等. 壓縮感知中迂回式匹配追蹤算法[J]. 計算機研究與發展, 2014, 51(9): 2101-2107)

[6]Chen S S B, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159

[7]Mohimani H, Babaie-Zadeh M, Tutten C. A fast approach for overcomplete sparse decomposition based on smoothedl0norm[J]. IEEE Trans Information Theory, 2009, 57(1): 289-301

[8]Liu Wanjun, Wang Hongzhi, Wang Xianlong. Iterative shrinkage SL0 compressed sensing recovery algorithm[J]. Journal of Changchun University of Technology, 2014, 35(4): 434-437 (in Chinese)

(劉婉軍, 王宏志, 王賢龍. 迭代收縮SL0壓縮感知恢復算法[J]. 長春工業大學學報, 2014, 35(4): 434-437)

[9]Zhao Ruizhen, Lin Wanjuan, Li Hao, et al. Reconstruction algorithm for compressive sensing based on smoothedl0norm and revised Newton method[J]. Journal of Computer-Aided Design & Computer Graphics, 2012, 24(4): 478-484 (in Chinese)

(趙瑞珍, 林婉娟, 李浩, 等. 基于光滑l0范數和修正牛頓法的壓縮感知重建算法[J]. 計算機輔助設計與圖像學學報, 2012, 24(4): 478-484)

[10]Yang Lianglong, Zhao Shengmei, Zheng Baoyu, et al. The improved reconstruction algorithm for compressive sensing on SL0[J]. Signal Processing, 2012, 28(6): 834-841 (in Chinese)

(楊良龍, 趙生妹, 鄭寶玉, 等. 基于SL0壓縮感知信號重建的改進算法[J]. 信號處理, 2012, 28(6): 834-841)

[11]Wang Junhua, Huang Zhitao, Zhou Yiyu, et al. Robust sparse recovery based on approximatel0norm[J]. Acta Electronica Sinica, 2012, 46(6): 1185-1189 (in Chinese)

(王軍華, 黃知濤, 周一宇, 等. 基于近似l0范數的穩健稀疏重構算法[J]. 電子學報, 2012, 40(6): 1185-1189)

[12]Xiang Gao, Zhang Xiaoling, Shi Jun. Complex-valued sparse reconstruction via arctangent regularization[J]. Signal Processing, 2014, 104(6): 450-463

[13]Li Ying, Wang Ze, Wang Junhua, et al. Sparse signal reconstruction based onl0norm approximation minimization[J]. Computer Engineering and Application, 2015, 51(10): 200-204 (in Chinese)

(李穎, 王澤, 王軍華, 等. 基于l0范數近似最小化的稀疏信號重構方法[J]. 計算機工程與應用, 2015, 51(10): 200-204)

[14]Qi Huanfang, Xu Yuanhao. Improved SL0 algorithm for compressive sensing signal reconstruction[J]. Electronic Science & Technology, 2015, 28(4): 27-30 (in Chinese)

(齊煥芳, 徐源浩. 用于壓縮感知信號重建的SL0改進算法[J]. 電子科技學報, 2015, 28(4): 27-30)

[15]Wu Feiyun, Zhou Yuehai, Tong Feng. A fast sparse signal recovery algorithm based on approximatel0norm and hybrid optimization[J]. Acta Automatica Sinica, 2014, 40(10): 2145-2150 (in Chinese)

(伍飛云, 周躍海, 童峰. 基于似零范數和混合優化的壓縮感知信號快速重構算法[J]. 自動化學報, 2014, 40(10): 2145-2150)

[16]Shi Jun, Ding Renhuan, Xiang Gao, et al. Complex-valued sparse recovery via double-threshold sigmoid penalty[J]. Signal Processing, 2015, 114: 231-244