基于PSO-BP預測模型的盾構機密封艙土壓平衡控制

李 強，李景軒

(西安理工大學 自動化與信息工程學院，陜西 西安 710048)

0 引言

盾構機是一種集電氣、機械、液壓、測量及控制等多學科技術于一體的大型電液設備，專門應用于地下隧道工程，它具有施工速度快、自動化程度高、安全性高、對地面建筑影響小、對環境影響小等優點。在盾構的掘進過程中，維持密封艙土壓平衡是非常重要的。掘進時，為了減少對土體造成的擾動、防止因為地表變形而引起災難性事故的發生，必須對密封艙土壓進行準確的控制，保持開挖面的壓力平衡。由于傳統的司機控制模式具有一定的滯后性，如何準確預測及控制密封艙土壓成為了盾構掘進領域的一個熱點[1-3]。密封艙壓力平衡的控制是多變量控制，需要綜合考慮刀盤、推進系統和螺旋輸送機等因素的影響。實際中，維持密封艙土壓平衡主要憑借操作者的經驗去調節螺旋輸送機轉速或推進速度，尚未實現該過程自動控制[4]。因此，已有學者對此展開了深入研究。文獻[5]基于盾構掘進的原理，對掘進過程的數學物理參數進行了分析，初步建立了盾構掘進的物理模型。文獻[6]采用神經網絡的方法對密封艙土壓建立預測模型。文獻[7]采用自適應神經網絡模糊推理(ANFIS)的方法對密封艙土壓進行的預測，但是此類方法學習收斂速度慢，容易陷入局部最優，實時的學習能力和泛化能力較差。為了得到更加準確的密封艙土壓和施工參數之間的關系，文獻[8]利用小型盾構機模型進行了實驗研究，得到了密封艙壓力、總推進力、螺旋輸送機轉速以及刀盤扭矩等參數之間的關系。

由于盾構機的推進速度受到密封艙土壓、頂進油缸扭矩、推力等多方面因素的影響，推進速度的改變必然會連帶影響其他參數。因此，本文綜合考慮了刀盤扭矩對密封艙壓力的影響，首先基于PSO-BP算法建立了密封艙土壓預測模型，提前一步預測下一時刻的土壓，然后結合PSO算法得到最優的螺旋輸送機轉速，作用于密封艙土壓平衡的控制過程，有效提高了控制的精度。

1 盾構掘機理模型描述

1.1 盾構掘進過程的連續性方程

在盾構機掘進過程中，假設各組油缸推進推力和刀盤轉速不變，且盾構機沒有出現超推進和欠推進狀態，則盾構機處于正常穩定掘進狀態，刀盤切削進入密封艙的原狀土量和排出量相等，則盾構處于土壓平衡狀態，此時密封艙進土量為：

Vi=πR2ΔS

(1)

其中：Vi為盾構機推進ΔS距離應排除的原狀土體積；R為刀盤半徑。

螺旋輸送機出土量的控制是維持土壓平衡盾構機土壓平衡的關鍵，螺旋輸送機出土量與轉速的關系為：

Q0=ηANL

(2)

(3)

其中：Qo為螺旋輸送機排土量；η為排土效率；A為螺旋輸送機有效斷面積；N為螺旋輸送機轉速；L為螺旋輸送機葉片間距；D1為螺旋輸送機直徑；D2為螺旋輸送機軸直徑。

ΔT時間內螺旋輸送機的出土量為：

dG=ηANLdT

(4)

其中：dG為單位時間內螺旋輸送機排土量。

在盾構的施工過程中，為了改良土質，會在密封艙中加入添加劑對渣土進行塑化處理。考慮添加劑重量，則有效土比為：

(5)

其中：dG天然為單位時間內排出的天然土重量，計算公式如式(6)所示；dG添加為單位時間內排出的添加劑重量。

dG天然=KeηANLdT

(6)

若γ0為天然土容重，則dT時間內排出的天然土體積為：

(7)

密封艙內渣土流量連續性方程[7]為：

(8)

其中，cep為土倉外部泄露系數；pe為土倉內土壓力；po為土倉外泄露壓力，po≈0；ve為土倉容積；βe為土倉土料、液體、氣體的有效壓縮系數；Vi和V天然分別為密封土倉渣土的進入和出土量。

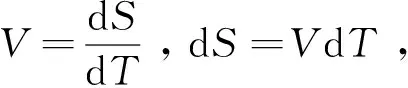
(9)

1.2 土壓和推力及刀盤轉速的關系

以整個盾構機為研究對象，有力學方程：

F-f-P=ma

(10)

其中：F為盾構機推進油缸所提供的總推力；f為推進時總阻力；P為刀盤和開挖面土體接觸壓力；m為盾構機總質量；a為盾構機推進加速度。由于盾構機推進速度較為緩慢，故認為盾構機加速度a為零。故有下式：

F=f+P

(11)

其中總阻力f包括：盾構側面與周邊地層的摩擦阻力；刀具貫入土體所受到的抵抗力；盾構姿態調整或者曲線施工的附加阻力；盾體和管片之間的摩擦力；后配套設備的牽引力。

另外，對于面板式盾構機，其面板上的土壓力要比土壓倉壓力大一個附加值δ，故有下式：

(12)

其中：λ為刀盤開口率；其他符號意義同上。將式(12)代入(11)可以得到土壓和推力的關系：

(13)

將式(13)做如下轉換可以得到：

(14)

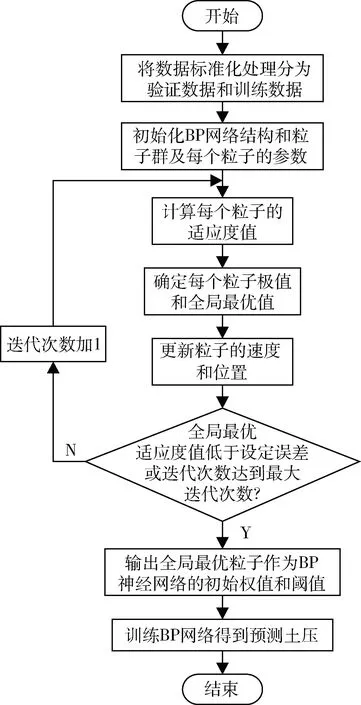
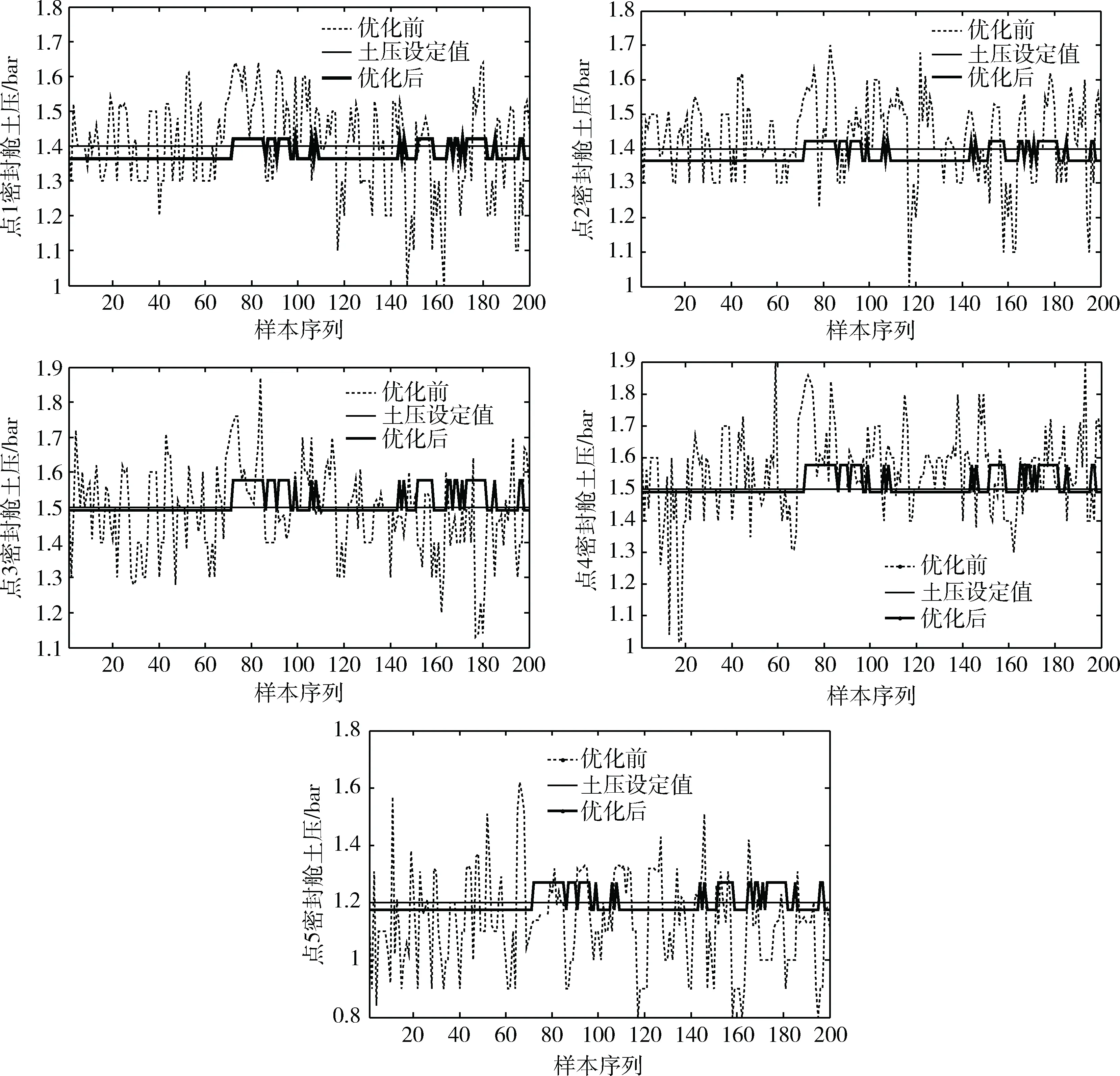
刀盤實際作用的土壓為P，且有：主動壓力

因為刀盤上面土壓力分布的狀態很有可能會因為開挖面的局部坍塌而變化，所以P可以用下式表示[9]：

(15)

p′和q′分別是從刀盤中心沿p軸和q軸到刀盤上一個點所測量到的距離與刀盤的半徑R的比值；n為刀盤旋轉速度；r為刀盤上計算點的半徑；σno是法向靜止土壓力，計算公式如式(16)所示；a、b為常數，這兩個值的范圍為-1～1；F(p′)和F(q′)分別為土壓沿p軸和q軸變化的狀態因數。

σno=Kσvo

(16)

其中，K為側向土壓力系數。初始垂直土壓力σvo為(對于粘性土壤)：

σvo=(Hc+rcosθ)γ

(17)

其中：Hc為地面到盾構機軸線的距離；θ為任意方向；r為刀盤上點到中心距離；γ為土的重度。

對于粘性土刀盤水平土壓力計算公式為：

(18)

將式(18)和式(13)帶入式(11)可得：

δ(1-λ)

(19)

式(19)即為土壓與刀盤轉速關系式。

1.3 刀盤扭矩和密封艙壓力的關系

刀盤扭矩是盾構機掘進過程中的一個重要參數,是保證盾構正常掘進、安全運行的關鍵參數之一。當盾構機推進速度過快或推進壓力過大時會導致刀盤扭矩的急劇上升，此時會造成密封艙土壓的相應增大，導致刀盤卡死甚至刀盤損壞。刀盤扭矩主要包括摩擦扭矩、切削扭矩和攪拌扭矩，文獻[10]從影響刀盤扭矩因素的角度給出刀盤扭矩切削關系表達式：

(20)

其中，Tn為刀盤切削扭矩；φ為土體內摩擦角；C為切削面土體的粘聚力。從式(12)和式(20)可以得出刀盤扭矩和密封艙土壓的關系，表明了刀盤扭矩會對密封艙土壓產生影響。文獻[8]指出了影響刀盤扭矩的主要因素是盾構面板和開挖面土體的接觸壓力即刀盤面板土壓，并通過擬合刀盤扭矩和密封艙土壓的關系證明了這一點。但是在實際中單純通過數學物理推導刀盤扭矩和密封土倉壓力之間的關系比較困難，因此文獻中給出了刀盤扭矩和密封艙土壓以及刀盤轉速之間的關系表達式：

M=kcnPe

(21)

式中：M為刀盤扭矩；kc為與刀盤形式、土體有關的參數。

通過上述分析可知盾構密封艙土壓與盾構推進速度、總推進力、螺旋輸送機轉速以及刀盤扭矩之間具有非線性的耦合關系，當前土壓可表示為：Pe=f(V,F,N,M)。

由于盾構掘進過程是一個復雜、非線性、多變量且掘進參數之間具有強耦合性的工業對象，較難有效辨識出機理模型參數，因此，本文采用PSO-BP算法來實現盾構機密封艙土壓的預測。

2 基于PSO-BP的密封艙土壓預測模型建立

2.1 基于粒子群優化BP神經網絡的算法

由于BP神經網絡存在易陷入局部最優、收斂速度慢的缺點，因此采用群體智能優化算法中的粒子群算法對BP神經網絡的權值和閾值進行優化。粒子群算法優化的基本原理[11-12]是：在一個D維的搜索空間中，有n個粒子會搜索最優解，在每次迭代過程中，粒子會通過粒子個體極值和種群全局極值更新自身的速度和位置，更新公式為：

(22)

(23)

式中：w為慣性權重；Vid為第i個粒子的第d個速度分量；Xid為粒子位置；Pid為個體極值；Pgd為全局極值；k為當前迭代次數；C1和C2為學習因子；r1和r2為[0,1]范圍內的隨機數。

PSO-BP神經網絡算法具有收斂速度快、精度高且不受模型結構影響的優點，兼顧了網絡初始閾值和權值的優化，具有更小的訓練誤差和檢驗誤差，提高了網絡的學習和泛化能力[13-14]。PSO-BP流程圖如圖1所示。

圖1 PSO-BP流程圖

2.2 預測模型的建立

盾構密封艙采用5個壓力傳感器實時采集密封艙土壓，分別安裝在承壓板上側、左上、右上、左下和右下位置，如圖2所示，5點土壓值分別為P1、P2、P3、P4、P5。以密封艙上點P1點壓力傳感器采集的數據為例進行仿真實驗。

圖2 密封艙壓力傳感器分布位置

因為需要優化螺旋輸送機轉速，所以將下一時刻的螺旋輸送機轉速也作為模型的輸入變量，以推進速度V(t)、總推進力F(t)、刀盤扭矩M(t)、當前時刻螺旋輸送機轉速N(t)、下一時刻螺旋輸送機轉速N(t+1)和當前時刻密封艙土壓值Pe(t)作為模型的輸入變量,X=(V(t),F(t),M(t),N(t),N(t+1),Pe(t))，以下一時刻密封艙土壓Y=Pe(t+1)作為模型的輸出，因此盾構機密封艙土壓預測模型的形式為：

Pe(t+1)=f(V(t),F(t),M(t),N(t),N(t+1),

Pe(t))

使用的BP神經網絡結構如圖3所示。

圖3 預測模型BP神經網絡結構

3 仿真實驗及分析

3.1 工程概況

為驗證模型的有效性和可行性，采集武漢某地下隧道施工現場設備400組s數據，隧道埋深在20～25 m之間。采用德國海瑞克公司的直徑為6.28 m的土壓平衡式盾構機，通過PLC和上位機監控系統[15]實時采集盾構機上的各種數據并存儲到數據庫中，參數主要包括密封艙5點土壓、總推進力、刀盤扭矩、掘進速度、螺旋輸送機轉速、油缸壓力和行程等。

選擇施工現場傳感器采集的200組數據作為訓練集進行訓練，另外200組數據作為驗證。在進行仿真實驗之前需要對輸入數據進行歸一化處理：

(24)

本次仿真采用均方誤差函數MSE來評價該預測模型的性能和預測效果。MSE的值越小，則證明模型的預測性能越好，其計算公式為：

(25)

3.2 PSO-BP神經網絡土壓預測模型仿真

BP神經網絡結構為6-15-1三層結構，網絡隱含層傳遞函數采用S型的對數函數tansig，輸出層采用線性函數purelin，訓練函數采用trainlm，學習函數采用learngdm，網絡的訓練次數為2 000次，學習的效率為0.05，網絡訓練目標誤差為0.000 1。

設定粒子種群規模為30，最大允許迭代次數為300，加速度因子C1=C2=1.494 45，對初始粒子的速度和位置賦隨機值，規定精度為0.05。參數初始化完成之后對粒子群算法進行編程模擬。

圖4給出了在相同的數據條件下，PSO-BP神經網絡與傳統BP神經網絡密封艙土壓預測值與實際土壓值的對比。圖5給出了PSO-BP與傳統BP神經網絡密封艙土壓預測誤差曲線對比。可以明顯看出，PSO-BP算法的預測精度明顯優于BP神經網絡。

圖4 PSO-BP和BP神經網絡土壓仿真結果

通過以上的對比分析可以很明顯地看出基于粒子群算法優化的BP神經網絡對密封艙土壓的預測精度更高，很好地修正了BP神經網絡土壓預測的誤差，表明粒子群算法對BP神經網絡的初始權值和閾值具有很好的優化效果。

4 基于粒子群算法的螺旋輸送機轉速優化

在盾構掘進的過程中，密封艙的土壓平衡控制主要是通過調整螺旋輸送機轉速實現[16]。結合上文密封艙土壓預測模型，以密封艙5點土壓預測值與各點土壓設定值的偏差最小為目標函數，采用粒子群算法對螺旋輸送機轉速進行優化，得到最優的螺旋輸送機轉速并將其反饋到液壓驅動系統，從而保證密封艙的土壓平衡控制，即找到N(t+1)使得：

圖5 神經網絡誤差曲線

圖7 5點土壓優化前后對比

(26)

Nmin≤N(t+1)≤Nmax

(27)

圖6 PSO優化螺旋輸送機轉速

通過圖7可以看出,經過PSO優化螺旋輸送機轉速之后的密封艙各點土壓波動小，而且與設定值誤差較小，說明此方法能夠很好地對密封艙進行土壓平衡控制，維持刀盤開挖面的穩定性，保證施工的安全。采用粒子群算法對控制模型進行優化的過程所需時間不到50 s，為盾構控制參數的調整提供了充足的時間。采用排土控制模式對密封艙土壓進行調節，降低了系統的耦合性，使盾構系統更加穩定高效，說明了此控制策略在實際工程中的可行性。

5 結論

本文提出了采用掘進機理與PSO-BP神經網絡算法相結合的方法建立盾構推進過程中的土壓預測模型，在此土壓預測模型的基礎之上提出了采用PSO粒子群智能算法對螺旋輸送機轉速進行實時優化的方法，并進行了仿真驗證分析。實驗結果表明，粒子群智能算法能夠很好地優化神經網絡的連接權值和閾值，模型控制精度和速度得到了提高。采用PSO算法對控制參數進行優化調整，使下一時刻的密封艙土壓能夠很好地跟隨土壓設定值，有效地保證密封艙土壓平衡，避免因密封艙壓力失衡而造成地表的坍塌或隆起。

參考文獻

[1] MASHIMO H. State of the road tunnel safety technology in Japan[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2002, 17(2):145-152.

[2] REILLY J J. The management process for complex underground and tunneling projects[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2000, 15(1):31-44.

[3] SHIN H S, KWON Y C, JUNG Y S, et al. Methodology for quantitative hazard assessment for tunnel collapses based on case histories in Korea[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(6):1072-1087.

[4] 劉宣宇, 邵誠. 盾構機自動控制技術現狀與展望[J]. 機械工程學報, 2010, 46(20):152-160.

[5] 朱合華, 徐前衛, 鄭七振,等. 軟土地層土壓平衡盾構施工參數的模型試驗研究[J]. 土木工程學報, 2007, 40(9):87-94.

[6] YEH I C. Application of neural networks to automatic soil pressure balance control for shield tunneling [J]. Automation in Construction, 1997, 5(5):421-426.

[7] 施虎, 龔國芳, 楊華勇,等. 盾構掘進土壓平衡控制模型[J]. 煤炭學報, 2008, 33(3):343-346.

[8] 王洪新, 傅德明. 土壓平衡盾構掘進的數學物理模型及各參數間關系研究[J]. 土木工程學報, 2006, 39(9):86-90.

[9] 管會生. 土壓平衡盾構機關鍵參數與力學行為的計算模型研究[D]. 成都：西南交通大學, 2007.

[10] 王洪新. 土壓平衡盾構刀盤扭矩計算及其與盾構施工參數關系研究[J]. 土木工程學報, 2009,42(9):109-113.

[11] SUWANSAWAT S, EINSTEIN H H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling[J]. Tunnelling & Underground Space Technology, 2006, 21(2):133-150.

[12] 洪亮, 李瑞娟. 基于粒子群算法優化BP神經網絡的色彩空間轉換[J]. 包裝工程, 2014,35(9):105-109.

[13] 張捍東, 陶劉送. 粒子群優化BP算法在液壓系統故障診斷中應用[J]. 系統仿真學報, 2016,28(5):1186-1190.

[14] 郭亞強, 王鵬, 白艷萍. 基于PSO-BP神經網絡的矢量水聽器的DOA估計[J]. 傳感技術學報, 2016, 29(8):1229-1233.

[15] 鄭朝虹. 地鐵盾構機傳感器應用技術[J]. 地下工程與隧道, 2009(3):17-18.

[16] SHAO C, LAN D. Optimal control of an earth pressure balance shield with tunnel face stability[J]. Automation in Construction, 2014, 46(10):22-29.