大跨度橋梁PK箱梁斷面顫振性能研究

方根深, 楊詠昕, 葛耀君

(同濟(jì)大學(xué) 土木工程防災(zāi)國家重點(diǎn)實(shí)驗(yàn)室,上海 200092)

為了適應(yīng)跨江跨海等工程需求，現(xiàn)代橋梁結(jié)構(gòu)在設(shè)計理論、施工技術(shù)逐漸成熟的保證下，向跨度更大、體系更柔的方向發(fā)展，同時鋼材的廣泛使用，又使結(jié)構(gòu)自重減輕、阻尼降低。這必然導(dǎo)致結(jié)構(gòu)對風(fēng)的敏感性增加，特別是1940年老Tacoma橋的風(fēng)毀事故引起了工程界對結(jié)構(gòu)抗風(fēng)的高度重視，風(fēng)振可靠度驗(yàn)證成為了大跨度橋梁結(jié)構(gòu)設(shè)計的關(guān)鍵環(huán)節(jié)。顫振是一種氣體與彈性結(jié)構(gòu)相互作用的氣動彈性現(xiàn)象，一旦發(fā)生將會對橋梁結(jié)構(gòu)造成災(zāi)難性的破壞。因此，研究大跨度橋梁的顫振性能是長期安全使用的重要保證。目前針對大跨度橋梁的顫振穩(wěn)定性已經(jīng)有了較為系統(tǒng)的研究[1-3]。而對于顫振發(fā)生的物理解釋，特別是不同橋梁斷面帶來的顯著差異以及各氣動措施的作用機(jī)理，還有待進(jìn)一步探討和完善。Matsumoto等[4]采用分步分析(step by step)的方法，將顫振分析分為扭轉(zhuǎn)和豎彎兩個運(yùn)動分支，研究了顫振發(fā)展過程中系統(tǒng)阻尼、剛度的變化，初步解釋了顫振發(fā)生機(jī)理。Yang等[5-6]進(jìn)一步分析了顫振臨界狀態(tài)各自由度的參與程度，同時解釋了部分結(jié)構(gòu)措施和氣動控制措施的作用機(jī)制。

PK箱梁斷面最早源于美國Pasco-Kennewick橋[7]，該橋首次采用了雙邊三角形箱梁的主梁形式，此后工程界將這種半開口分離雙箱斷面簡稱為PK斷面，在近幾年越來越多的被運(yùn)用到實(shí)際工程中，特別是寬主梁雙索面密索體系大跨徑斜拉橋，如鄂東長江大橋、荊岳長江大橋等。PK斷面主梁橫向剛度較大，而且相比于閉口箱梁可以節(jié)省下底板的材料用量，同時在氣動性能方面整體表現(xiàn)良好。已有研究表明，PK箱梁斷面主要存在+3°或+5°風(fēng)攻角的大幅豎彎渦振現(xiàn)象[8-10]，同時根據(jù)風(fēng)洞試驗(yàn)提出了抑流板這一有效控制措施[11]，而抑流板對顫振性能的影響有待研究。與此同時，在荊岳長江大橋的全橋氣彈風(fēng)洞試驗(yàn)中還發(fā)現(xiàn)，成橋狀態(tài)下，-3°風(fēng)攻角時顫振安全儲備充足，而+3°風(fēng)攻角時臨界風(fēng)速(實(shí)橋56 m/s)比0°(實(shí)橋98.4 m/s)低了43%；孟曉亮等[12]對70°風(fēng)嘴椒江二橋的試驗(yàn)中也發(fā)現(xiàn)成橋運(yùn)營狀態(tài)的+3°風(fēng)攻角顫振臨界風(fēng)速(114 m/s)比0°時(200 m/s)也要低43%，有必要對這種風(fēng)攻角高敏感性作出解釋；朱樂東等[13]發(fā)現(xiàn)PK箱梁斷面橋梁存在復(fù)雜的軟顫振現(xiàn)象，在不同風(fēng)速和風(fēng)攻角下，會有軟顫振需要初始激勵、大振幅激勵發(fā)散、小振幅激勵衰減、軟顫振之后緩慢發(fā)散四種現(xiàn)象，同時其試驗(yàn)結(jié)果表明+3°和+5°風(fēng)攻角顫振臨界風(fēng)速基本不變，但是比0°風(fēng)攻角小了接近75%。可見，PK斷面顫振性能復(fù)雜，一方面需要在對不同風(fēng)攻角下復(fù)雜的顫振現(xiàn)象有了定性認(rèn)識的基礎(chǔ)上，能夠解釋風(fēng)攻角敏感性問題，另一方面希望能夠?qū)ふ液线m氣動措施，在提高正風(fēng)攻角下氣動失穩(wěn)臨界風(fēng)速的基礎(chǔ)上，對渦振控制也能起到有利作用，以期PK斷面在山區(qū)存在大風(fēng)攻角以及沿海高設(shè)計風(fēng)速地帶能有更廣闊的發(fā)展空間。

目前關(guān)于PK箱梁斷面顫振性能較完整的研究較少，本文以某大跨度混合梁斜拉橋?yàn)檠芯勘尘埃猿蓸驙顟B(tài)的PK斷面為基本斷面，進(jìn)行了節(jié)段剛體模型風(fēng)洞試驗(yàn)，并結(jié)合理論分析，研究了其顫振穩(wěn)定性能。在此基礎(chǔ)上，探討了抑流板對其顫振性能的影響，為該種斷面的廣泛使用所需要的抗風(fēng)設(shè)計提供參考。

1 風(fēng)洞試驗(yàn)與顫振性能

1.1 基本斷面與風(fēng)洞試驗(yàn)

PK箱梁斷面寬38.5 m，高3.425～3.8 m，橋面坡度2%，底板開口寬度13.9 m，橫隔板設(shè)置間距為3 m，如圖1所示。本文設(shè)計了幾何縮尺比例λL=1∶70的剛體節(jié)段模型，選用彈簧懸掛二元剛體節(jié)段模型方法進(jìn)行顫振試驗(yàn)，在滿足幾何外形相似基礎(chǔ)上，保持彈性參數(shù)(頻率比)、慣性參數(shù)(慣性半徑比)、阻尼參數(shù)(阻尼比)相似，各參數(shù)取值見表1。

表1 顫振節(jié)段模型風(fēng)洞試驗(yàn)主要參數(shù)

試驗(yàn)在同濟(jì)大學(xué)TJ-2大氣邊界層風(fēng)洞中進(jìn)行，選用四個通道高精度激光位移傳感器進(jìn)行振動信號采集。動力特性和顫振導(dǎo)數(shù)的測試采用自由振動法，并通過修正最小二乘法識別顫振導(dǎo)數(shù)[14]。PK箱梁斷面實(shí)橋外形尺寸與節(jié)段模型風(fēng)洞試驗(yàn)布置分別見圖1和圖2。

圖1 PK箱梁橫斷面圖(單位:mm)

圖2 彈簧懸掛節(jié)段模型風(fēng)洞試驗(yàn)與測量儀器

Fig.2 Spring-suspended sectional model system and measuring instrument

1.2 顫振性能

顫振臨界風(fēng)速是評價橋梁結(jié)構(gòu)顫振性能的關(guān)鍵指標(biāo)，同時關(guān)注顫振發(fā)展的過程，即結(jié)構(gòu)隨風(fēng)速增長各動力參數(shù)變化過程是認(rèn)識顫振現(xiàn)象的重要途徑。因此，本文重點(diǎn)關(guān)注顫振臨界風(fēng)速、顫振形態(tài)以及阻尼比、顫振導(dǎo)數(shù)等隨風(fēng)速增大的變化情況。

1.2.1 原斷面顫振性能

如圖3和圖4所示，RMS(Root Mean Square)為均方根值，在一定風(fēng)速范圍內(nèi)，成橋狀態(tài)的PK斷面存在著較穩(wěn)定的扭轉(zhuǎn)振動，且振幅隨風(fēng)速增大而增大，即為 “軟顫振”現(xiàn)象，是一種單模態(tài)的、由自激力非線性引起的結(jié)構(gòu)自平衡狀態(tài)[15]，由于氣動偏心(扭轉(zhuǎn)中心往來流上游側(cè)偏移)作用表現(xiàn)為彎扭自由度耦合的振動形態(tài)。

圖3 +3°風(fēng)攻角下“軟顫振”現(xiàn)象(實(shí)橋風(fēng)速64.35 m/s)

Fig.3 “Soft flutter” phenomenon at attack angle of +3°(wind speed is 64.35 m/s)

圖4 原始斷面不同風(fēng)攻角下扭轉(zhuǎn)角根方差

從圖4～圖6可以看出，PK箱梁斷面在+3°風(fēng)攻角下較低風(fēng)速就表現(xiàn)出顫振特點(diǎn)，而0°風(fēng)攻角顫振風(fēng)速提高接近了一倍，-3°風(fēng)攻角則在試驗(yàn)風(fēng)速下未發(fā)生顫振現(xiàn)象。在進(jìn)入“軟顫振”風(fēng)速區(qū)間時，系統(tǒng)阻尼比趨于0，大振幅激勵下會逐漸衰減到穩(wěn)定振幅。

圖5 原始斷面不同風(fēng)攻角下扭轉(zhuǎn)響應(yīng)峰值因子

Fig.5 Peak factor of torsional angle at different attack angles of original section

1.2.2 抑流板對顫振性能的影響

朱樂東等研究表明典型橋梁斷面的“軟顫振”有別于傳統(tǒng)的“硬顫振”，其臨界風(fēng)速很難通過改變結(jié)構(gòu)阻尼比或者橋面附屬結(jié)構(gòu)大幅度提高。本文在風(fēng)洞試驗(yàn)中，發(fā)現(xiàn)抑流板能夠在有效抑制PK箱梁斷面渦振的基礎(chǔ)上，大幅度提高其在+3°風(fēng)攻角下的顫振臨界風(fēng)速，對0°和-3°風(fēng)攻角的臨界風(fēng)速影響較小，能夠有效達(dá)到工程需求目標(biāo)。因此，對抑流板這一有效氣動措施進(jìn)行了+3°風(fēng)攻角下較為細(xì)致的研究。

圖6 原始斷面不同風(fēng)攻角下扭轉(zhuǎn)阻尼比

Fig.6 Damping ratio for torsional motion at different attack angles of original section

抑流板設(shè)計如圖1所示，安裝在最外側(cè)檢修道欄桿頂部，與水平夾角15°，并進(jìn)行了三種寬度尺寸的比較，與檢修道欄桿高度比值分別為η=0.57,η=1.14,η=1.71。圖7～圖9為+3°風(fēng)攻角下原斷面與安裝了抑流板后主梁響應(yīng)特征，可以看出，添加抑流板能夠較大幅度提高顫振起振風(fēng)速；隨著板寬的增大，起振風(fēng)速有增大的趨勢，但逐漸表現(xiàn)出了“硬顫振”的特點(diǎn)，特別是η=1.71的抑流板，當(dāng)實(shí)橋風(fēng)速U=83.76 m/s時，在自由振動和一定激勵作用下，扭轉(zhuǎn)角度都會大幅增加。

1.2.3 顫振臨界風(fēng)速

由于對“軟顫振”的風(fēng)速臨界點(diǎn)沒有較明確的規(guī)定，本文基于性能設(shè)計的思想，采用了扭轉(zhuǎn)角根方差大于0.5°、峰值因子PF值小于2以及系統(tǒng)阻尼比等于0的綜合評定方法，取對應(yīng)的最小風(fēng)速為顫振臨界風(fēng)速。表2給出了以上各工況對應(yīng)的臨界風(fēng)速。

圖7 +3°風(fēng)攻角下扭轉(zhuǎn)角根方差

圖8 +3°風(fēng)攻角下扭轉(zhuǎn)阻尼比

Fig.8 Damping ratio for torsional motion at attack angle of +3°

圖9 +3°風(fēng)攻角下扭轉(zhuǎn)峰值因子

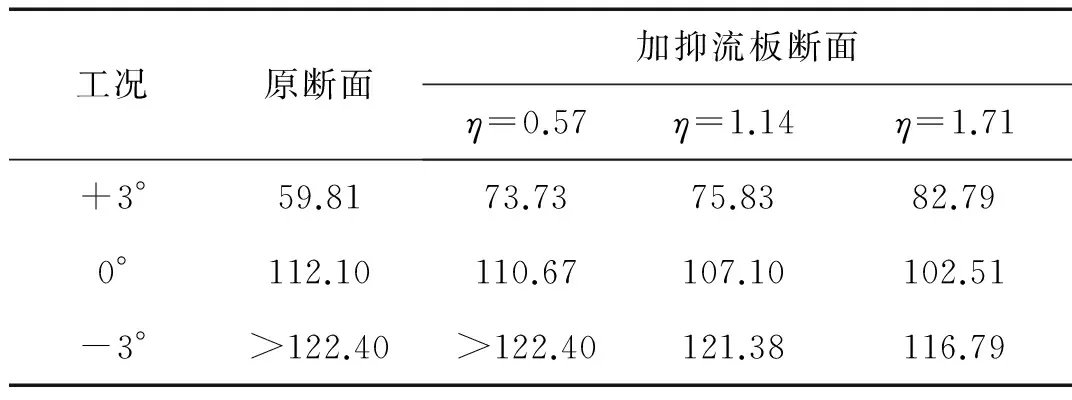
工況原斷面加抑流板斷面η=0.57η=1.14η=1.71+3°59.8173.7375.8382.790°112.10110.67107.10102.51-3°>122.40>122.40121.38116.79

可以看出，原斷面+3°風(fēng)攻角下臨界風(fēng)速較低，比0°風(fēng)攻角下低了46.6%，表現(xiàn)出顯著的風(fēng)攻角效應(yīng)；抑流板可以有效提高+3°風(fēng)攻角下的臨界風(fēng)速，增大幅度隨板寬增大而呈現(xiàn)增大趨勢，η=0.57,η=1.14和η=1.71時，臨界風(fēng)速分別增大23.3%,26.8%,38.4%。同時，試驗(yàn)中也進(jìn)行了抑流板對0°和-3°風(fēng)攻角顫振影響的研究，其臨界風(fēng)速有減小的趨勢，但是在試驗(yàn)工況范圍內(nèi)減小的幅度不大，且此時臨界風(fēng)速仍然遠(yuǎn)大于+3°風(fēng)攻角下的結(jié)果。

1.2.4 顫振導(dǎo)數(shù)

2 顫振驅(qū)動機(jī)理解釋

雖然“軟顫振”是由自激力的非線性效應(yīng)引起的，但基于Scanlan頻域線性顫振理論，可以建立能同時研究二維橋梁節(jié)段模型扭轉(zhuǎn)、豎向和側(cè)向振動參數(shù)(系統(tǒng)阻尼及系統(tǒng)剛度)，與氣動外形參數(shù)(氣動導(dǎo)數(shù))的定量關(guān)系，從而清晰的認(rèn)識顫振發(fā)展過程中的結(jié)構(gòu)系統(tǒng)剛度、阻尼的變化，解釋顫振驅(qū)動機(jī)理。因此，本文從頻域角度對PK箱梁斷面顫振的攻角效應(yīng)和抑流板的作用機(jī)理作出解釋。

2.1 二維三自由度(2D-3DOF)顫振分析理論

基于Scanlan在頻域的線性顫振理論，定義主梁運(yùn)動的三個主要自由度為x={p,h,α}T；可以將二維三自由度的運(yùn)動方程寫為

(a)顫振導(dǎo)數(shù)

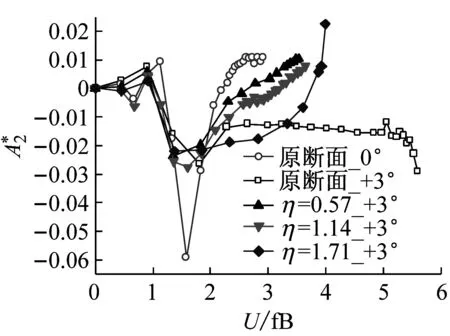
(b)顫振導(dǎo)數(shù)

(c)顫振導(dǎo)數(shù)

(1)

式中:M={mp,mh,Iα}、C0={cp,ch,cα}和K0={kp,kh,kα}分別為三個自由度的廣義質(zhì)量、廣義阻尼和廣義剛度;Cae和Kae分別為氣動阻尼矩陣和氣動剛度矩陣;Fb為抖振力(強(qiáng)迫力)。

Matsumoto等、Yang等和Ge等通過引入不同自由度運(yùn)動之間的激勵-反饋機(jī)制來解耦顫振運(yùn)動方程組，從而對系統(tǒng)扭轉(zhuǎn)牽連運(yùn)動、豎向牽連運(yùn)動和側(cè)向牽連運(yùn)動進(jìn)行求解。下面僅考慮豎向和扭轉(zhuǎn)兩個自由度，扭轉(zhuǎn)牽連運(yùn)動方程可以表達(dá)為

(2)

式中:ξα0和ωα0分別為扭轉(zhuǎn)牽連運(yùn)動的結(jié)構(gòu)阻尼比和固有圓頻率，等號右邊三項(xiàng)分別表示扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動力、扭轉(zhuǎn)速度項(xiàng)耦合豎向運(yùn)動產(chǎn)生的氣動力以及扭轉(zhuǎn)位移項(xiàng)耦合豎向運(yùn)動產(chǎn)生的氣動力，分別為

(3)

表3 扭轉(zhuǎn)牽連運(yùn)動氣動剛度與氣動阻尼比

(6)

式中:第一個量描述了耦合豎向運(yùn)動的參與程度;第二個量則描述了扭轉(zhuǎn)主運(yùn)動的參與程度，該矢量在平面幾何坐標(biāo)單位圓上的位置可以直觀反映相對參與程度。

2.2 原始斷面顫振的顯著攻角效應(yīng)

由于-3°攻角在試驗(yàn)風(fēng)速內(nèi)未出現(xiàn)顫振現(xiàn)象，此處僅討論0°攻角與+3°攻角顫振性能的顯著差異。0°攻角、+3°攻角氣動阻尼比和系統(tǒng)阻尼比變化規(guī)律如圖11和圖12所示。可以看到，0°攻角時，AD_A項(xiàng)和AD_D項(xiàng)起控制作用，其他氣動阻尼項(xiàng)作用甚微；AD_A項(xiàng)即由扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動阻尼為正值，且隨風(fēng)速先逐漸增大后小幅降低，而后緩慢增大逐漸趨于穩(wěn)定，對系統(tǒng)氣動穩(wěn)定性起到有利作用；而由扭轉(zhuǎn)主運(yùn)動的位移項(xiàng)所產(chǎn)生的耦合氣動升力激發(fā)起的耦合豎向運(yùn)動，其速度所產(chǎn)生的氣動升力矩反饋到扭轉(zhuǎn)主運(yùn)動，這一激勵-反饋?zhàn)饔弥骶€表現(xiàn)在AD_D項(xiàng)，其在風(fēng)速達(dá)到一定數(shù)值時隨風(fēng)速增大逐漸減小，對系統(tǒng)穩(wěn)定性起到不利作用；以上氣動阻尼項(xiàng)與系統(tǒng)機(jī)械阻尼比之和等于0時，系統(tǒng)趨于發(fā)散，此時風(fēng)速為102.15 m/s，比試驗(yàn)風(fēng)速低了8.9%。+3°攻角時，AD_A項(xiàng)起主要控制作用，其他四項(xiàng)氣動阻尼影響很小；AD_A項(xiàng)隨風(fēng)速增大先迅速增大，在達(dá)到峰值后又迅速減小并變?yōu)樨?fù)值，逐漸抵消系統(tǒng)機(jī)械阻尼比而驅(qū)動系統(tǒng)發(fā)散，此時風(fēng)速為62.82 m/s，比試驗(yàn)風(fēng)速高了5%。

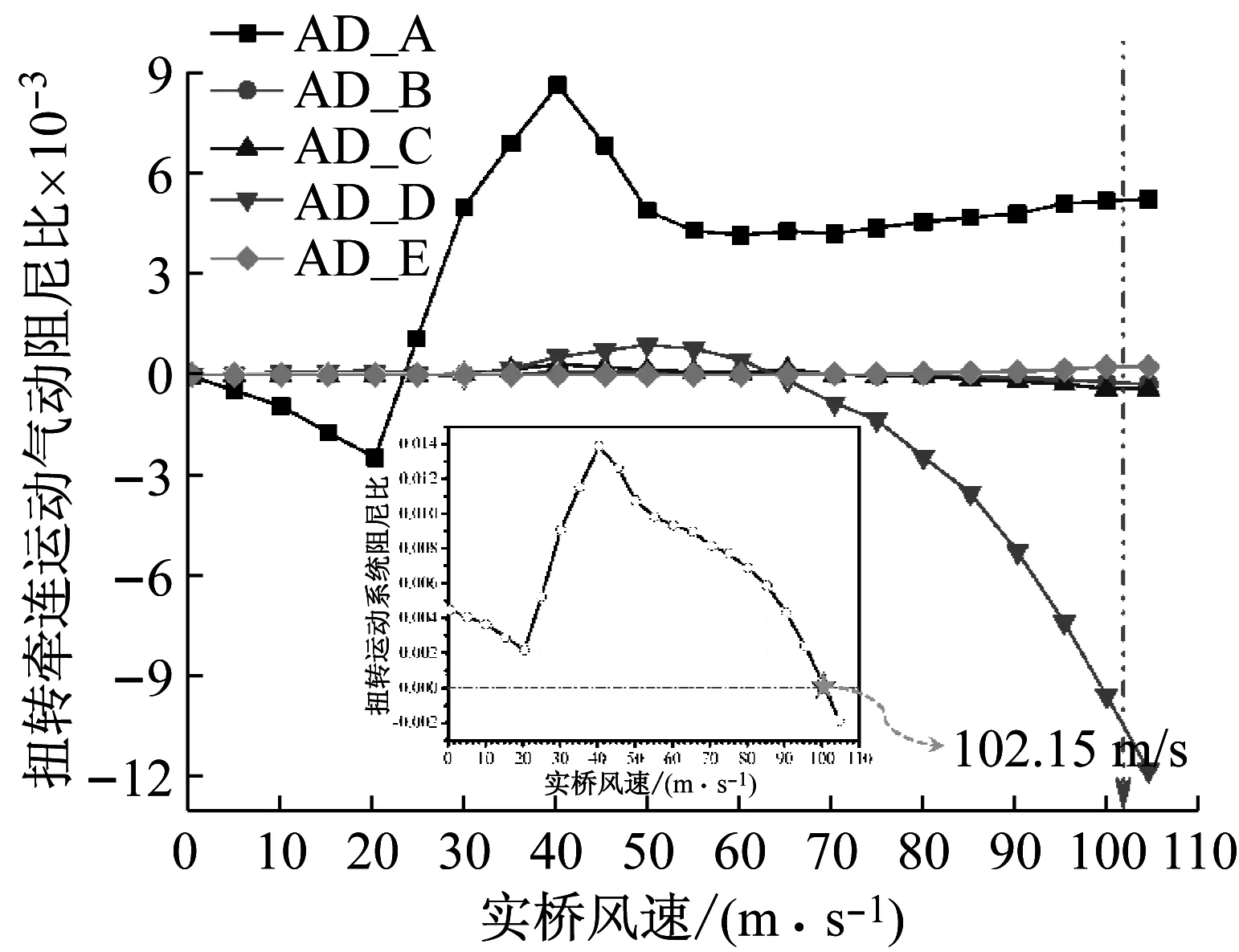
圖11 原始斷面0°風(fēng)攻角下氣動阻尼比變化規(guī)律

Fig.11 Aerodynamic damping ratio of original section at attack angle of 0°

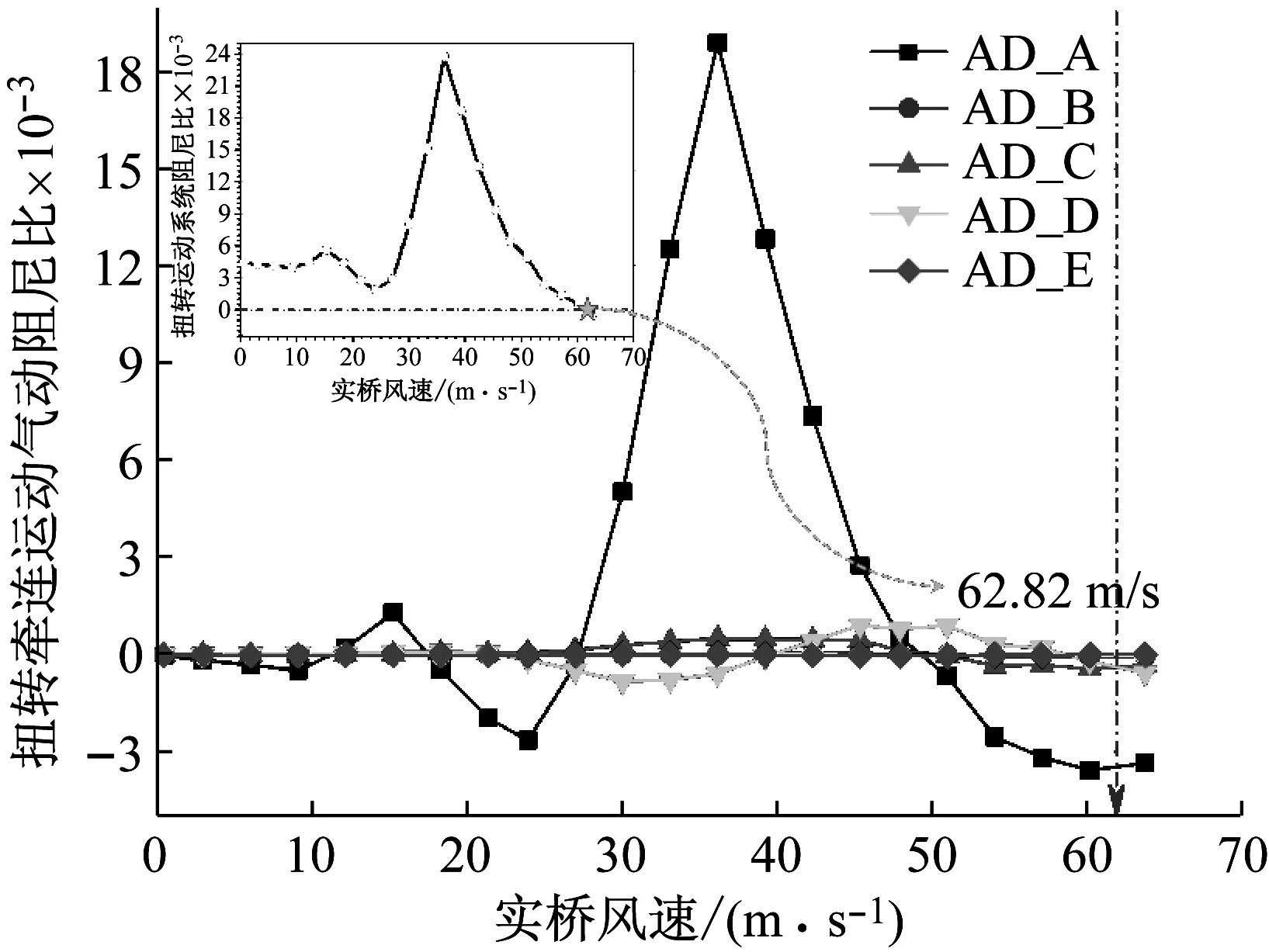
圖12 原始斷面+3°風(fēng)攻角下氣動阻尼比變化規(guī)律

Fig.12 Aerodynamic damping ratio of original section at attack angle of +3°

比較兩個攻角氣動阻尼可以發(fā)現(xiàn)，0°攻角下系統(tǒng)表現(xiàn)為明顯的“彎扭耦合顫振”，耦合運(yùn)動的氣動負(fù)阻尼是驅(qū)動系統(tǒng)發(fā)散的主要原因，但是扭轉(zhuǎn)運(yùn)動自身氣動阻尼對系統(tǒng)穩(wěn)定作用明顯，并隨風(fēng)速增大有緩慢的增強(qiáng)；而+3°攻角下系統(tǒng)表現(xiàn)為典型的“單自由度扭轉(zhuǎn)顫振”，耦合作用很微弱，扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動阻尼變化劇烈，由正轉(zhuǎn)負(fù)過程迅速，主導(dǎo)了系統(tǒng)的發(fā)散。因此，兩個攻角下顫振性能差異顯著，+3°攻角顫振臨界風(fēng)速也會比0°攻角小很多。

2.3 抑流板顫振作用機(jī)理

抑流板對PK斷面+3°攻角的顫振性能起到有效的改善作用，其氣動阻尼比與風(fēng)速變化關(guān)系如圖13所示。可以看出，添加了抑流板后，相比于圖12，系統(tǒng)在高風(fēng)速雖然耦合氣動負(fù)阻尼項(xiàng)逐漸表現(xiàn)出來，但是扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動阻尼項(xiàng)減小速度變緩，并與負(fù)阻尼相互競爭，而提高了系統(tǒng)的顫振臨界風(fēng)速。隨著板寬的增大，系統(tǒng)耦合氣動阻尼比AD_D項(xiàng)都會在風(fēng)速約為55 m/s時隨風(fēng)速增大而逐漸減小，而AD_C項(xiàng)(即由扭轉(zhuǎn)主運(yùn)動的速度項(xiàng)所產(chǎn)生的耦合氣動升力激發(fā)起的耦合豎向運(yùn)動，其位移所產(chǎn)生的氣動升力矩反饋到扭轉(zhuǎn)主運(yùn)動的阻尼項(xiàng))也逐漸表現(xiàn)出不利作用，由此可見，板寬越大，高風(fēng)速下耦合氣動阻尼的不利作用將越發(fā)明顯；但是AD_A項(xiàng)的減小速率也很快放緩，顯然，抑流板對本文中的PK箱梁斷面是有利的，在一定風(fēng)速范圍內(nèi)，使得AD_A項(xiàng)在氣動阻尼的競爭中占主導(dǎo)地位從而提高了顫振臨界風(fēng)速。然而，對于抑流板的控制作用需要進(jìn)一步結(jié)合橋梁斷面表面壓強(qiáng)以及氣流形態(tài)等進(jìn)行比較，其對不同外形PK箱梁斷面顫振性能提升的有效性以及普適性有待進(jìn)一步結(jié)合風(fēng)洞試驗(yàn)確定。

2.4 自由度耦合程度

橋梁斷面達(dá)到顫振臨界狀態(tài)時，扭轉(zhuǎn)和彎曲兩個自由度的耦合程度可以從顫振形態(tài)矢量反映出來(見式(6))，如圖14所示，半徑大小代表了顫振臨界狀態(tài)的風(fēng)速，矢量坐標(biāo)點(diǎn)橫縱坐標(biāo)的相對大小代表了豎彎和扭轉(zhuǎn)自由度的參與程度。可以看出，PK箱梁斷面整體上的顫振耦合程度較弱，原斷面+3°攻角豎向自由度參與程度很低，可以看作是“單自由度扭轉(zhuǎn)顫振”，而0°攻角雖然仍以扭轉(zhuǎn)自由度為主，但豎向自由度參與程度有所增大，即表現(xiàn)出耦合顫振特點(diǎn)；添加抑流板的斷面顫振形態(tài)矢量在兩者之間，而不同板寬對顫振形態(tài)影響不大。

(a) η=0.57

(b) η=1.14

(c) η=1.71

圖14 各斷面顫振形態(tài)矢量圖

3 結(jié) 論

本文借助風(fēng)洞試驗(yàn)并結(jié)合理論分析，進(jìn)行了PK箱梁斷面顫振性能研究，并對三種尺寸抑流板顫振控制效果與機(jī)理進(jìn)行探索，得到以下主要結(jié)論：

(1)PK箱梁斷面成橋狀態(tài)具有“軟顫振”特點(diǎn)，參考性能設(shè)計方法，本文提出扭轉(zhuǎn)角度根方差大于0.5°、扭轉(zhuǎn)響應(yīng)峰值因子小于2以及阻尼比小于0來綜合評定顫振臨界風(fēng)速。

(2)PK箱梁斷面顫振性能具有顯著的攻角效應(yīng)，即0°和±3°攻角下顫振臨界風(fēng)速差異明顯，主要是由于0°攻角時，系統(tǒng)表現(xiàn)出耦合顫振特點(diǎn)，扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動阻尼對系統(tǒng)有很強(qiáng)的穩(wěn)定作用，耦合氣動負(fù)阻尼逐漸驅(qū)動系統(tǒng)發(fā)散；+3°攻角時，系統(tǒng)表現(xiàn)出單自由度扭轉(zhuǎn)顫振特點(diǎn)，扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動阻尼變化劇烈，迅速由正轉(zhuǎn)負(fù)，主導(dǎo)系統(tǒng)顫振發(fā)散，而耦合氣動阻尼基本不起作用。

(3)抑流板能有效提高PK箱梁斷面+3°攻角的顫振臨界風(fēng)速，相比于原斷面，其會在高風(fēng)速激起耦合氣動負(fù)阻尼，而且板寬增大，AD_C項(xiàng)和AD_D項(xiàng)都表現(xiàn)出較大不利作用，然而扭轉(zhuǎn)運(yùn)動自身產(chǎn)生的氣動阻尼AD_A項(xiàng)由正轉(zhuǎn)負(fù)的速率變得緩慢，有利于系統(tǒng)的持續(xù)穩(wěn)定，以上兩方面氣動阻尼的競爭將決定系統(tǒng)最終的發(fā)散。

(4)PK箱梁斷面整體上的顫振耦合程度較弱，原斷面+3°攻角豎向自由度參與程度很低，可以看作是“單自由度扭轉(zhuǎn)顫振”，而0°攻角雖然仍以扭轉(zhuǎn)自由度為主，但豎向自由度參與程度有所增大，即表現(xiàn)出耦合顫振特點(diǎn)；添加抑流板的斷面顫振形態(tài)矢量在兩者之間，而不同板寬對顫振形態(tài)影響不大。

參 考 文 獻(xiàn)

[1] SIMIU E, SCANLAN R H. Wind effects on structures-fundamentals and applications to design[M]. 3rd ed. New York: John Wiley & Sons, 1996.

[2] 項(xiàng)海帆. 現(xiàn)代橋梁抗風(fēng)理論與實(shí)踐[M]. 北京: 人民交通出版社, 2005.

[3] 葛耀君. 大跨度懸索橋抗風(fēng)[M]. 北京: 人民交通出版社, 2011.

[4] MATSUMOTO M, DAITO Y, YOSHIZUMI F, et al. Torsional flutter of bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71: 871-882.

[5] YANG Y X, GE Y J, XIANG H F. Investigation on flutter mechanism of long-span bridges with 2d-3DOF method[J]. Wind and Structures, 2007, 10(5): 421-435.

[6] GE Y J, ZOU X J, YANG Y X. Aerodynamic stabilization of central stabilizers for box girder suspension bridges[J]. Wind and Structures, 2009, 12(4): 285-298.

[7] GIMSING N J, GEORGAKIS C T. Cable supported bridges-concept and design[M]. 3rd ed. New York: John Wiley & Sons, 2012.

[8] 王騎, 陶奇, 廖海黎, 等. 鄂東大橋主梁大尺度節(jié)段模型渦激振動特性試驗(yàn)研究[C]∥第十三屆全國結(jié)構(gòu)風(fēng)工程學(xué)術(shù)會議論文集. 大連: 人民交通出版社, 2007.

[9] 朱樂東, 張海, 張宏杰. 多孔擾流板對半封閉窄箱梁渦振的減振效果[J]. 實(shí)驗(yàn)流體力學(xué), 2012, 26(3): 50-55.

ZHU Ledong, ZHANG Hai, ZHANG Hongjie. Mitigation effect of multi-orifice flow-disturbing plate on vortex-induced resonance of narrow semi-closed box deck[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 50-55.

[10] 宋錦忠, 丁望星, 丁泉順, 等. 湖北荊岳長江公路大橋抗風(fēng)性能試驗(yàn)研究[C]∥第十四屆全國結(jié)構(gòu)風(fēng)工程學(xué)術(shù)會議. 北京:第十四屆全國結(jié)構(gòu)風(fēng)工程學(xué)術(shù)會議論文集, 2009.

[11] 方根深，楊詠昕，葛耀君，等. 半開口分離雙箱梁渦振性能及其氣動控制措施研究[J]. 土木工程學(xué)報,2017,50(3):74-82.

FANG Genshen, YANG Yongxin, GE Yaojun, et al. Vortex-induced vibration performance and aerodynamic counter measures of semi-open separated twin-box deck[J]. China Civil Engineering Journal, 2017,50(3):74-82.

[12] 孟曉亮，郭震山, 丁泉順, 等. 風(fēng)嘴角度對封閉和半封閉箱梁渦振及顫振性能的影響[J]. 工程力學(xué), 2011, 28(增刊1): 184-194.

MENG Xiaoliang, GUO Zhenshan, DING Quanshun, et al. Influence of wind faring angle on vortex-induced vibrations and flutter performances of closed and semi-closed box decks[J]. Engineering Mechanics, 2011, 28(Sup1): 184-194.

[13] 朱樂東，高廣中. 典型橋梁斷面軟顫振現(xiàn)象及影響因素[J]. 同濟(jì)大學(xué)學(xué)報(自然科學(xué)版), 2015, 43(9): 1289-1294.

ZHU Ledong, GAO Guangzhong. Influential factors of soft flutter phenomenon for typical bridge deck sections[J]. Journal of Tongji University(Natural Science), 2015, 43(9): 1289-1294.

[14] DING Quanshun, ZHOU Zhiyong, ZHU Ledong, et al. Identification of flutter derivatives of bridge decks with free vibration technique[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010,98(12): 911-918.

[15] 張朝貴. 橋梁主梁“軟”顫振及其非線性自激氣動力參數(shù)識別[D]. 上海: 同濟(jì)大學(xué), 2007.

[16] 公路橋梁抗風(fēng)設(shè)計規(guī)范:JTG/TD 60-01—2014[S]. 北京: 人民交通出版社, 2004.