基于裝配關系的驅動橋殼結構強度與模態分析

白寧山，侯鎖軍，范瑋衛，董二婷

（河南工學院 汽車工程系，河南 新鄉 453003）

作為車輛的主要承載零件，驅動橋殼同時承受車輛載荷和路面反作用力等設計時，應使驅動橋殼具備足夠的剛度和強度。由于其外形復雜，采用傳統的力學計算方法，僅能得出驅動橋殼某一截面的平均應力值。無法真實且完整地得到應力大小及其分布情況，需要借助長期的生產經驗進行結構設計及優化，不利于得到更優化的結構。驅動橋上的零件，尤其是鋼板彈簧對橋殼受力的影響較大，對單一驅動橋殼零件進行力學分析，并不能真實且完全地反映其受力情況。文章以驅動橋殼和鋼板彈簧等零件的裝配體為研究對象，對驅動橋殼的受力進行分析，并對單一驅動橋殼進行模態分析。本研究為橋殼設計及優化提供了更有效的理論依據。

1 驅動橋殼力學模型和車輛參數

根據傳統的力學計算方法，將驅動橋殼視為簡支梁，設計時，校核其危險截面的最大應力值。在車輛運行時，橋殼的受力情況復雜多變，設計時，需對其承受最大垂向力、最大牽引力、最大制動力和最大側向力等極限工況進行強度分析。研究車輛的參數如表1所示。

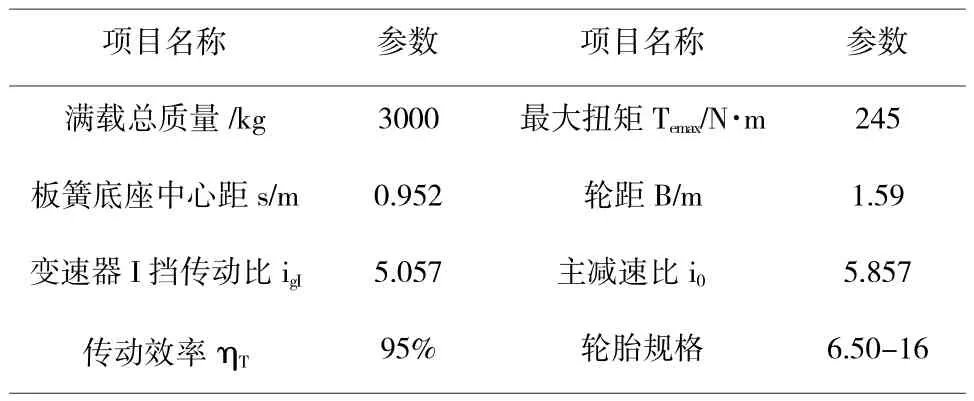
表1 研究車輛的參數表

2 有限元模型建立

依據驅動橋殼、鋼板彈簧、板簧底座和主減速器殼體的零件工程圖，使用Solidworks對各個零件進行參數化建模，并按照實際的裝配關系創建驅動橋殼裝配體模型，如圖1（a）所示。為提高分析的效率，在保證其計算精度的前提下，對研究模型進行假定：①忽略非關鍵區域的倒角、細孔等小尺寸結構；于忽略焊接位置的材料特性變化；③假定材料為均質。

圖1 驅動橋殼的裝配體模型

由于Solidworks與ANSYS可以無縫連接，通過Solidworks直接將實體模型導入到ANSYS Workbench中。選擇合適的單元類型及尺寸，劃分網格進而建立有限元模型，如圖1（b）所示。選用“Sweep法”對鋼板彈簧進行網格劃分，其他零件的單元類型均選用“solid187”，設置網格尺寸為0.015m。由于研究對象是裝配體，但期望得到的是驅動橋殼的受力情況，因此設置組件的接觸方式為：綁定、非對稱行為。橋殼的材料參數、約束條件和施加載荷的方式分別列在表2、表3和表4中。另外，主減速器殼體材料為QT450-10，鋼板彈簧材料為60Si2Mn，板簧底座材料為45。

表2 驅動橋殼的材料參數表

表3 驅動橋殼在各工況下的約束條件

表4 驅動橋殼在各工況下的載荷方式

3 結構靜力學分析

使用ANSYS Workbench對滿載、最大垂向力、最大牽引力、最大制動力和最大側向力共五種工況下的驅動橋殼裝配體模型進行結構靜力學分析，得到了驅動橋殼在各工況下的等效應力云圖和總體位移云圖，分別如圖2～圖6所示。

圖2 滿載工況的分析結果

圖3 最大垂向力工況的分析結果

圖4 最大牽引力工況的分析結果

圖5 最大制動力工況的分析結果

圖6 最大側向力工況的分析結果

由圖2可知，驅動橋殼在車輛滿載靜止時的最大等效應力值為56.1MPa，最大位移量為0.44mm。驅動橋殼每米輪距的最大變形量則為0.44mm/1.59m=0.28mm/m，滿足《汽車驅動橋臺架試驗方法》規定的垂直彎曲剛性試驗評估指標：不超過1.5mm/m。《汽車驅動橋臺架試驗方法》同時規定垂直彎曲靜強度試驗評估指標：Kn＞6，Kn的數學計算公式為：

Kn=Pn/P

式中，Pn為破壞載荷，P為滿載載荷。由于驅動橋殼材料的屈服強度為345MPa，因此，Kn=345/56.1=6.15，滿足垂直彎曲靜強度實驗評估指標。由圖3～圖6可知，在最大的垂向力、牽引力、制動力和側向力的工況下，驅動橋殼的最大等效應力值分別是：140.26MPa、177.08MPa、221.05MPa、253.42MPa，最大變形量分別是：1.1mm、1.28mm、1.28mm、0.43mm。這表明，在各工況下驅動橋殼均能滿足強度和剛性的指標。

由圖2～圖6可知，在各工況下，驅動橋殼最大應力出現在板簧底座兩端與驅動橋殼接觸的位置，此情況為局部應力集中，主要原因有：①鋼板彈簧變形導致該位置承受載荷較集中；于結構設計不合理。使用車輛時，鋼板彈簧變形無法避免，但可以對該位置的橋殼結構需要進行優化，如：在驅動橋殼應力較大位置內側增加襯套等，進而增強承載能力等。由此可見，有限元分析法在產品結構設計及優化方面具有很大的應用價值。

4 模態分析

在車輛行駛時，驅動橋殼承受輪胎動不平衡和路面的激勵。作為驅動橋殼設計的重要研究項目，模態分析通過識別系統的模態參數來確定振型和固有頻率等振動特征，是車輛動載荷結構設計和振動特征分析的基礎，為結構的振動故障診斷和預報、結構的動態特征優化提供依據。

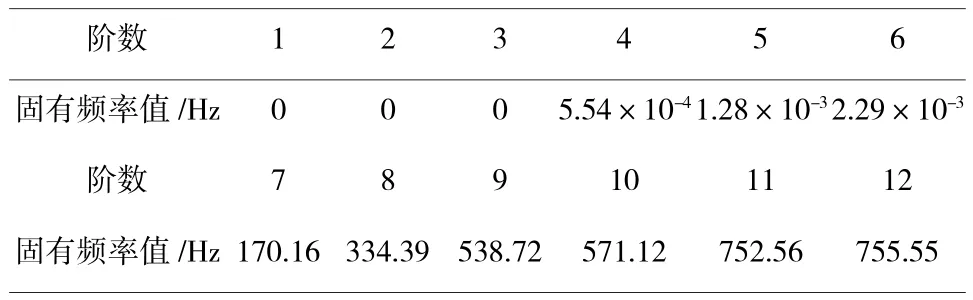
表5 各階模態的固有頻率值

各階模態的振型通過線性關系組成結構的振動特征，低階模態的振型是最基本的，與高階模態的振型相比，對結構的動態特征起決定性作用，具有更大的研究意義。ANSYS Workbench軟件提供了多種線性的實特征值提取方法來求解結構的振型和固有頻率，文章采用計算速度較快和計算精度較高的分塊蘊anczos法。忽略系統的阻尼對其振動特征的影響，對驅動橋殼模型不施加任何載荷和約束，使其完全處于懸空的狀態，因此，第1～6階振型的固有頻率幾乎是零，文章研究的前6階基本振型實際上是第7～12階的振型，其固有頻率值如表5所示。

文章研究的前6階模態的振型圖如圖7所示。

圖7 前6階模態的振型圖

從圖7可以看出，驅動橋殼的基本振型主要表現為彎曲和扭轉，那么，更高階的振型便是彎扭組合。第1～4階振型分別是Z軸彎曲變形、Y軸彎曲變形、繞Z軸扭轉變形和繞Y軸扭轉變形，振動的相對位移最大的位置均為橋殼兩端軸承安裝處；第5～6階振型分別是繞X軸扭轉變形和X軸彎曲變形，振動的相對位移最大的位置均為安裝主減速器殼體的法蘭盤處。在設計驅動橋殼時，應當加強驅動橋殼兩端軸承安裝位置和安裝主減速器殼體的法蘭盤位置的剛度。

文章研究的前6階基本振型對應的固有頻率值依次是：170.97Hz、328.16Hz、532.9Hz、561.85Hz、749.13Hz、792.57Hz，在車輛行駛時，驅動橋殼承受不平路面激勵的頻率范圍是：0～50Hz，文章研究的低階模態的固有頻率均遠遠高于50Hz，不會引起驅動橋殼共振，符合結構設計要求。

5 結語

利用Solidworks創建驅動橋殼模型，通過ANSYS Workbench進行結構靜力學分析，得到了驅動橋殼在各工況下的等效應力分布和變形情況，更真實詳細地反映出了驅動橋殼在車輛運行時的受力和變形情況，分析結果表明驅動橋殼滿足強度和剛度的結構設計要求。通過模態分析，得到驅動橋殼的低階模態的振型和固有頻率值，通過對比得出，驅動橋殼不會因不平路面等激勵而引起共振，符合動態設計要求。

有限元分析結果也明確顯示出局部應力集中和振動相對位移較大的位置，為驅動橋殼的進一步優化和輕量化設計提供了依據，將極大地提高產品的更新速度，并降低新產品的開發成本。

參考文獻

［1］劉惟信.汽車車橋設計［M］.北京：清華大學出版社，2004.

［2］M.M.Topa，H.Günal，N.S.Kuralay.Fatigue failure prediction of a rear axle housing prototype by using finite element analysis［J］.Engineering Failure Analysis，2009，（16）：1474-1482.

［3］Yimin Shao，Jing 蘊iu，Chris K.Mechefske.Drive axle housing failure analysis of a mining dump truck based on the load spectrum［J］.Engineering Failure Analysis，2011，（18）：1049-1057.

［4］Ningshan Bai，Anyuan Jiao，Shiming 蘊iu.Finite element analysis of drive axle housing with ANSYS Workbench［J］.Applied Mechanics and Materials，2012，（2）：717-720.

［5］焦安源，李宗澤，白寧山.基于協同仿真環境的貨車驅動橋殼有限元分析［J］.制造業自動化，2014，（2）：31-33.

［6］陳國榮，唐紹華.汽車驅動橋橋殼強度與模態的有限元分析［J］.機械設計與制造，2010，（2）：42-44.

［7］孫輝，王吉忠，沙德文，等.微型車驅動橋殼結構強度與模態分析［J］.機械設計與制造，2011，（8）：219-221.