常微分方程在數學建模中的應用
覃 游
(四川師范大學附中,四川 成都 610000)
當前,常微分方程是很多理工科專業設置的一門基礎課程。與微積分相似,常微分方程也是人類認識世界、改造世界不可或缺的一個數學工具。在長年累月的生產實踐中,常微分方程已經演變成了數學領域對理論和實踐相聯系的重要分支,而利用常微分方程建立數學模型,也成為了解決很多實際問題的重要手段。因此,對常微分方程在數學建模中的應用展開探究,有著非常重要的意義。
1 常微分方程在腐敗人數預測模型中的應用
當前,人們經常在電視或網絡上看到很多政府官員因為腐敗問題而落馬的報道,而這些腐敗官員的落馬往往會牽扯出大量的涉案分子,這些被牽扯出來的涉案分子往往會采取東躲西藏的方式來逃避法律對他們的制裁。為此,可以用常微分方程來進行數學建模和創新,利用這些被牽扯出的涉案分子的人數來對總涉案人數加以預測,建立出一個新的腐敗人數預測模型,這包括以下三個步驟。
(1)假設階段。設t表示時間,x(t)表示這個腐敗集團所牽扯的涉案分子的總人數有關t的函數,X0表示在t=0時刻這個腐敗集團所牽扯的涉案分子的總人數,r(x)表示牽扯涉案分子的增長率,r表示在x0時刻牽扯的涉案分子人數的增長率,也稱作固有增長率,xm表示這個腐敗事件可能會牽扯的最多人數,μ表示在追查時產生的阻力系數,i(t)表示這個腐敗事件所牽扯人數在總人數中的比例,λ表示在t=0時刻這個腐敗事件所牽扯人數在所有人數中的比例,λ表示已被抓到的每個腐敗分子在每個月之內所招供出的平均人數。
(2)分析階段。若已牽扯出的腐敗分子人數呈現出了遞增趨勢,就說明潛在的腐敗分子人數正在逐漸減少。x(t)表示這個腐敗事件牽扯的人數與時間t之間的函數關系,x(t)是與t有關的連續函數,其中的一個上界是xm,牽連人數對應的增長率r(x)和x(t)之間也存在特定的函數關系。從前面的假設可知,r(x)是x的一條線性函數。r(x)=r-kx(k表示斜率,k>0)。當x=xm時,涉案人數的增長率是0,r(xm)=0,這樣就能確定k=r/xm,那么所牽扯的涉案人數的增長率函數就能夠用r(x)=r(1-x/xm)來加以計算。
(3)計算階段。在不考慮偵察的力度以及偵查的困難程度可能給偵查結果帶來影響的情況下,可以建立出以下的微分方程:
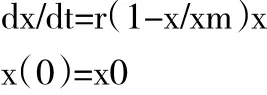
解得
在考慮偵查的困難程度可能給偵查結果帶來影響的情況下,可以將阻力系數設為μ,從而建立出以下的微分方程:
di/dt=λi(1-i)-μi
i(0)=i0(λ≠μ)
解得
這個數學模型可以作為我國的反腐敗部門在今后的反腐敗工作當中對腐敗分子牽連的人數進行預測的方法,不難發現,在理論上計算出的腐敗人數與實際工作當中所查出的腐敗人數有著非常近似的誤差范圍。
2 常微分方程在生物種群數量模型中的應用
(1)研究背景。目前,生物種群的數量問題是一個非常熱門的問題,這個問題引起了世界范圍內眾多專家和學者的廣泛關注。想要對某個生物種群在未來的數量進行預測,主要的影響因素就是這一生物種群在目前的總數目,以及這一生物總群在未來一段時間內的增長情況和其所處環境的影響因素。當某一生物的種群數目增加到一個特定的程度之后,這一種群的生物就并將在狹小的生存空間中相互競爭,并且種群中各個生物的增長狀況會在種群數目不斷增加的狀況下出現削減。因此,對該生物種群在未來的數目,就可以通過建立生物種群數量模型的方式來解決。
(2)Malthus模型。如果想對未來一段時間中該生物種群的總體數目進行推測,那么所涉及到的主要特征就是數學刻畫,即該生物的自然增長率,這是確定該生物在一段時間內種群的增量和種群的數量之間比例系數的有效手段,同時還能反映出在一段時間內,該生物中某個單個個體的平均增加量,其自然增長率既能作為常數,又能作為變數。
可以用t表示時間,用常數λ表示該生物種群所對應的自然增長率。假設在該生物種群所生存的環境下,只存在這一種生物種群,或其它的生物種群的存在不會對該生物種群的生存造成影響。在t時刻,該生物種群的數量可以表示為N(t),但是N(t)的數量是非常龐大的,所以可將其視作時間t的連續可微函數。假設在t=0的時刻,這個生物種群的數量用N0來表示,那么在△t這一時段內,該生物種群數量的凈增加量就可以用t垣△t時刻該生物種群的數量減去t時刻該生物種群的數量來計算出來,其常微分方程為:
N(t垣△t)N(t)=λN(t)△t
根據這個常微分方程,可以建立出Malthus模型:
dN(t)/dt=λN(t)
N(0)=N0
解得 N(t)=N0eλt
從這個結果可以看出,上面所建立的數學模型在結果上是和19世紀之前歐洲各大地區統計出的人口數據完全吻合的。另外,從這個方程還可以得知,在一些地廣人稀的地區,其人口的增長情況更加符合這種模型,并呈現出指數增長的趨勢,這就證明這種假設與數學建模的方式是非常合理的。
(3)蘊ogistic模型。在使用Malthus模型的過程中,人們發現,Malthus模型對于19世紀之后的人口統計數據與實際相比存在著較大的差異,這就表明Malthus模型在應用上是有一定的局限性。隨著生物種群的數量在不斷地增加,外界的自然資源和環境等因素對各種生物種群數量所產生的阻滯作用也愈發突出,也就是說,Malthus模型當中所提出自然增長率的合理性并不是在任何情況中都適應的。為此,可以對其加以創新,將其改進為蘊ogistic模型。
在蘊ogistic模型中,可以假設某種生物種群所對應的自然增長率與其種群數量的函數關系為f(N),并用Nm表示該生物種群所在的環境能夠容納的最大數量。在進行數學建模時,通常要將未知函數的處理過程表示為線性函數或二次函數的形式,可以假設f(N)=ax垣b是這一線性函數,那么由f(Nm)=0可知,f(N)=λ(1-N/Nm)。將其改進為logistic模型:
dN/dt=λ(1-N/Nm)N
N(0)=N0
解得
利用這一模型與10世紀到20世紀的美國人口統計數據進行對比,可以發現兩者是完全吻合的,這就證明蘊ogistic模型能夠合理地表示出生物種群的數量在外界環境制約下出現的變化情況。
3 常微分方程在人口預測模型中的應用
由于地球上的資源存在有限性的特點,所以世界上的各個國家都已經開始有計劃地對人口的增長情況進行控制。想要建立準確的人口預測模型,就必須先弄清楚影響人口增長的因素有哪些。實際上,影響人口增長的因素非常多,如自然出生率、自然死亡率、人口遷移、戰爭、自然因素等等,如果在初始階段就對所有的因素都加以考慮,那么模型的建立就會無從下手。因此,可以先對問題進行簡化,建立出一個較為粗糙的數學模型,然后再對其進行逐步地修改,從而得到一個相對完善的數學模型。
1838年,荷蘭著名的數學家韋爾侯斯特將常數Nm引入到了數學建模中,并用其表示自然環境能夠容許的最大人口數。一般而言,一個國家的工業化水平越高,這個國家的生活空間就越大,Nm也就越大。韋爾侯斯特假設,增長率可以表示為r(1-Nt/Nm),而凈增長率則會隨著Nt的增大而逐漸減少,當Nt逐漸趨近于Nm時,凈增長率則會逐漸趨近于零,利用這一假定就能夠建立出人口預測模型。所以,可以利用韋爾侯斯特的理論進行創新,建立出一個新的人口預測模型。
dN/dt=r(1-N/N0)N
N(t0)=N0
這個常微分方程建立出的數學模型是一種邏輯模型,可以對其進行分離變量處理,其解為:
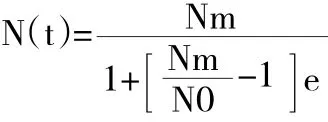
根據這個人口預測模型,并結合韋爾侯斯特的相關理論,就能夠對人口的增長情況進行合理的預測了。
4 結語
綜上所述,文章主要對常微分方程在數學建模中的應用進行了詳細的分析,并對一些以往的數學模型進行了改進,并利用常微分方程創新性地設計出了一些新的數學模型,并將其應用在了不同領域的問題研究當中。希望廣大的數學領域的專家和學者們能夠對常微分方程在數學建模中的應用展開更加深入的研究,創造出更多的數學模型,從而解決社會上的一些復雜課題。
參考文獻
[1]李寶萍.常微分方程在數學建模中的應用[J].赤峰學院學報(自然科學版),2012,28(21):1-2.
[2]方芳.常微分方程理論在數學建模中的簡單應用[D].合肥:安徽大學,2010.
[3]谷成玲.常微分方程在數學建模中的應用[J].數學學習與研究,2016,(3):89.

