阿爾奇公式的適用條件分析及對策

楊克兵 王競飛 馬鳳芹 唐海洋 潘雪峰

1.中國石油華北油田分公司勘探開發研究院, 河北 任丘 062552；2.中國石油大學(華東)地球科學與技術學院, 山東 青島 266580；3.中國石油華北油田分公司第一采油廠, 河北 任丘 062552

0 前言

電阻率測井在20世紀20年代就已誕生,但當時人們沒有清楚地認識巖石電阻率的響應關系,只能用電阻率資料定性識別油、氣、水層,還可劃分巖性和進行地層對比,并不能用它定量解釋和評價儲層。直到1942年阿爾奇公式發表以后,研究人員才以阿爾奇公式為基礎建立了一套儲層含油氣飽和度的定量評價技術,在測井理論與測井實踐間建立了聯系[1]。此后,研究人員根據各自的巖樣重復阿爾奇的實驗,取得巖電參數,用于含油飽和度計算。實際應用表明,以單井少量巖樣得出的巖電參數并不能滿足對全井段或區塊儲層的解釋,某些層含油飽和度計算誤差較大,影響油水層評價。針對這些問題,研究人員依據地質條件修正阿爾奇公式,派生出各種各樣的引申公式來提高含油飽和度的計算精度[2-5]。即使這樣,這些公式在泥質砂巖、低阻儲層、復雜孔隙儲層使用效果也不是太好[6-10]。這讓研究人員意識到巖電參數的可靠性對于計算精度的影響,因而對阿爾奇公式的巖電參數進行了大量研究[11-15],提出了一系列關于巖電參數物理意義、不同巖性變化的認識,取得了一定效果,但并沒有完全解決問題。實際解釋計算中仍有一些不吻合的層,研究人員把這些歸結于地質條件與阿爾奇公式的實驗條件不吻合,或歸結于導電模式的復雜化使得阿爾奇公式不適應[16-17],其實還是阿爾奇公式的適用條件問題。因此,繼續深入分析阿爾奇公式的適用條件是非常重要的,不僅有助于提高對巖石電阻率響應關系的認識,還可為提高測井解釋符合率提供依據。

1 對阿爾奇公式的主要認識回顧

阿爾奇公式的基本原理有兩方面：一是飽含水儲層電阻率與該儲層所含水的電阻率(即地層水電阻率)成正比,其比例系數稱為地層因子,用F表示；二是儲層含油時的電阻率與該儲層飽含水時的電阻率成正比,其比例系數稱為電阻率指數,用I表示。通過巖電實驗,所確立的關系式為：

(1)

(2)

根據進一步研究發現[18-20],由于砂巖的非均質性及膠結程度的差異等,地層因子與孔隙度的關系是有比例系數的,并不是簡單的1。同理,這一觀點也被應用到電阻率指數上,則阿爾奇公式變為：

(3)

(4)

上述公式通過替換Ro,可合并為電阻率與含水飽和度的關系式,即為電阻率測井定量評價儲層含油氣飽和度的公式(阿爾奇公式)：

(5)

式中：F為儲層飽含水時的電阻率與地層水電阻率比值,無量綱；I為儲層飽含油時的電阻率與儲層飽含水時的電阻率比值,無量綱；Ro為純水層巖石電阻率,Ω·m;Rt為儲層巖石電阻率,Ω·m；Rw為儲層地層水電阻率,Ω·m；Φ為儲層巖石孔隙度,小數；Sw為儲層巖石含水飽和度,小數；a、b、m、n為巖電試驗回歸參數。

阿爾奇公式認為儲層電阻率與儲層孔隙度、含水飽和度及地層水電阻率等的大小相關,在巖電參數a、b、m、n及地層水電阻率Rw確定的情況下,儲層電阻率與儲層孔隙度及含水飽和度均成反比關系。如果儲層孔隙度、巖電參數已知,則含水飽和度與儲層電阻率之間的關系是唯一的。同時,在相同的地層參數條件下,通過阿爾奇公式只能得出高阻是油、低阻是水的結論,不能解決低阻油層的識別問題[21-22]。

一直以來,針對實際應用中存在的問題,測井解釋人員對阿爾奇公式的適用條件進行多年研究,認為有三個方面的限制因素[16-17]：

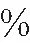
2)沒有考慮巖石泥質含量對導電的影響,認為巖石的骨架是絕緣體。實際上,因為黏土具有很大的比面,存在固有的表面負電荷,能吸附少量水分,具有形成偶電層的能力,因而泥質砂巖的骨架具有一定的導電性。而且,在自然界的復雜條件下,完全沒有泥質的砂巖是少見的。

3)沒有考慮儲層非均質性的影響,從實驗巖石性質上看,還隱含要求巖石的孔隙度在空間上的分布是均勻的；巖石中所含流體的飽和度在空間上的分布是均勻的；巖石中所含有的水不是淡水；巖石的電學性質是各向同性的。不過在復雜地質條件下,巖石的本質是不均勻和各向異性的,雖然各向異性現象在大尺度的宏觀條件下可能會較弱,但是對計算結果的影響是不可忽視的,在地層傾斜的情況下尤其如此。

可以看出,以往研究從實驗過程、對樣品的要求、與實際地層的差別等因素對阿爾奇公式的適用條件進行了分析,但這些因素對公式的具體影響程度并不明確,沒有實驗測量結果檢驗,大部分影響只是一種可能因素。比如泥質含量的影響,實際上使用含泥質的砂巖進行巖電實驗,所有數據表明其響應方程與純砂巖的形式并無二致,只是巖電參數與純砂巖有所不同[9-10]。低阻儲層砂巖也是如此,表明阿爾奇公式的函數關系式是可靠的,各種影響因素均可通過巖電參數的變化而消除。泥質砂巖、低阻儲層、復雜孔隙儲層與常規砂巖儲層的巖電參數是不一致的,參數的不一致才是產生含油飽和度計算誤差的主要原因[6-7,11]。因此,從巖電實驗數據本身對阿爾奇公式適用條件進行分析,尤其是使用參數的一致性分析,有助于問題的解決。

2 巖電實驗數據的適用條件分析

測井巖電實驗測量巖電參數a、b、m、n,為阿爾奇公式計算提供參數。過程如下：先把洗油后的巖樣用按照地層條件下配置的水溶液進行浸泡,然后一般采用氣吹方式降低巖樣的含水孔隙體積,對每塊巖樣測量4～8次,記錄電阻率的變化與可動水含量的變化,把一個區塊或單井的所有相同巖性、不同孔隙的巖樣測量完成后,對所有測量數據在雙對數坐標下進行回歸,得出巖電參數a、b、m、n。

回歸出a、m值用的是地層因子公式,見式(3)。從數學分析的角度可以看出,地層因子公式轉換為函數形式為：Ro=F(Φ)=aRwΦ-m,其中Ro是因變量,Φ是自變量,a、Rw、m是常數。根據巖電實驗的流程,對于單塊巖樣的測量結果來說,式(3)僅僅是一個等式而不是公式,因為每塊巖樣的測量數據里只有一個Ro與Φ。對于不同巖樣來說,式(3)可以作為公式,Ro是因變量,Φ是自變量,其中,a、Rw、m值是常數項。這表明,針對實驗所用的不同巖樣,常數項的特點要求其a、Rw、m值完全相同,這是建立回歸公式的前提條件。可以看出,這個前提條件也是阿爾奇公式的隱含適用條件。對于Rw值而言,采用相同濃度的液體浸泡洗油后的巖樣可以滿足。對a、m值而言,不同巖樣的a、m值是否相同至今未有定論,也沒有合適的檢驗方法,因此,阿爾奇本人也認為地層因素公式是合理觀測精度下可以接受的一種關系形式[16]。

回歸出b、n值用的是電阻率指數公式,見式(4)。從數學分析的角度可以看出,電阻率指數公式轉換為函數形式為：Rt=F(Ro,Sw)=bRoSw-n,其中Rt是因變量,Ro、Sw是自變量,b、n是常數。根據巖電實驗的流程,對于單塊巖樣的測量結果來說,Ro變成了常數,式(4)可以看做公式Rt=F(Sw)=b′Sw-n,因為每塊巖樣的測量數據就是Rt與Sw的變化,可直接應用。對于不同巖樣來說,式(4)是一個公式,與a、m值的確定原則一樣,即不同巖樣b、n值要完全相同,這一點也無法得到進一步確認,因而阿爾奇自己也認為I=Sw-n只是一個近似公式[16]。

通過上述分析可知,巖電實驗回歸參數a、b、m、n的獲取是一種典型的數學地質應用方法,它表明阿爾奇公式適用條件是對相同巖性、不同孔隙的巖樣,要求其a、b、m、n值完全一樣或大致接近,否則公式的使用精度將降低,所用巖樣的a、b、m、n值差距越大,則阿爾奇公式使用效果越差。而針對不同巖樣,當前并沒有可靠的方法獨立檢驗其a、b、m、n值是否一致,尤其是對單塊巖樣,無法得出其a、b、m、n值。這樣,在實際應用中當不同儲層巖電參數不一致時,將導致阿爾奇公式產生一些不符合現象[16]。

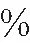
表1華北某區塊砂巖的巖電實驗數據阿爾奇公式的反算結果

巖樣編號氣吹次數/次測量電阻率/(Ω·m)Rt/Ro巖樣測量含水飽和度Sw/(%)反算儲層巖石電阻率Rt/(Ω·m)絕對誤差/(Ω·m)相對誤差/(%)26044.41.00100.044.40.00.00167.61.5276.269.21.62.33291.92.0763.892.40.50.503101.82.2961.697.74.14.014271.36.1133.5264.07.32.6940066.81.00100.066.80.00.00168.41.0295.372.33.95.672120.51.8085.486.434.128.333155.42.3360.1153.22.21.3941872.8052.8188.91.91.045217.43.2544.7247.830.413.98

3 適用條件意義及對策

3.1 意義

根據對阿爾奇公式的普遍認識,研究人員一直認為其存在的問題是理想化的實驗條件與復雜的地質情況的矛盾。針對實際中存在的泥質砂巖、低阻儲層、復雜孔隙儲層,主要通過使用引申公式或調整地層水性來解決問題[21-22]。對于同一口井的不同層位砂巖,一般采用相同參數處理,并沒有認識到不同砂層其巖電參數a、b、m、n也會存在不同,因而實際中存在的各種問題很難找到其產生原因,導致問題不易解決。

對巖電實驗數據分析認為阿爾奇公式適用條件是對相同巖性、不同孔隙的巖樣,要求其巖電參數a、b、m、n值完全一樣或大致接近,否則公式的使用精度將降低。這一觀點的提出,進一步豐富了阿爾奇公式的內涵,許多問題可迎刃而解。它表明實際處理中巖電參數a、b、m、n值受諸多因素影響,在使用時不應為一定值,要隨儲層性質的變化而變化。如泥質砂巖儲層,與純砂巖儲層使用不一樣的巖電參數就能解決問題。同理,低阻儲層、復雜孔隙儲層的解釋也可用同樣的原理解決。由此可見,這一條件是阿爾奇公式使用的最主要前提條件,大大增加了巖電參數在測井解釋評價中的重要性。

因此,這一認識揭示了阿爾奇公式的本質,對該公式今后的合理應用將產生一定影響。進一步通過實驗資料或測井曲線評價巖電參數的方法將會得到重視和發展,這是提高測井解釋符合率的有效途徑之一。

3.2 對策

當前在實際測井解釋中,并沒有一個好的方法來逐點、逐層評價儲層的a、b、m、n值,巖電參數不準確會使得計算的儲層含水飽和度產生誤差,進而影響對油氣水層的評價。如對于復雜孔隙結構儲層,傳統的阿爾奇公式計算出的含油飽和度偏低,導致解釋過程中漏失油層。要提高油水層評價的符合率,可從下述三方面開展工作：

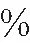
2)進一步對電阻率響應方程進行研究,提出新的能在實際中使用的公式。如有研究人員提出了一個僅有a、m值的電阻率響應方程[25],公式簡單,需要參數少,可以使用沖洗帶電阻率反算巖電參數,使用深電阻率計算儲層含油飽和度,可做逐點、逐層處理,具有較好的效果。

3)發展使用其它資料、方法、儀器來評價油水層,如可使用核磁共振等新方法評價油水層,避免了參數選擇的誤差[26-27]。還可使用電阻率比值法進行油水層評價及含油飽和度計算[28],該方法也不需要巖電參數,在有陣列感應資料的情況下是一種可靠的方法。

4 結論

1)通過對阿爾奇公式進行數學分析,認為阿爾奇公式適用條件是對相同巖性、不同孔隙的巖樣,要求其巖電參數a、b、m、n值完全一樣或大致接近,否則公式的使用精度將降低。而且不同砂層的巖電參數a、b、m、n值差距越大,則阿爾奇公式使用效果越差。這一結論是可靠的,符合公式使用的實際要求。

2)阿爾奇公式的函數關系式在泥質砂巖、低阻儲層及復雜孔隙儲層均吻合,表明實驗條件的差距、地質條件的變化、儲層的非均質性都不是阿爾奇公式使用影響因素,作為阿爾奇公式的適用條件依據并不充分。

3)地層不同孔隙的巖性真實巖電參數a、b、m、n值是多樣性變化的,而實際測井解釋中并沒有好的方法來逐點、逐層落實巖電參數a、b、m、n值,巖電參數不可靠是阿爾奇公式計算含油飽和度產生誤差的原因。即使采用不同的模型,如雙水模型、西門度方程等也解決不了這一問題。這表明獲得可靠巖電參數用于評價是阿爾奇公式需要解決的重要問題,對今后測井解釋具有指導意義,也為使用阿爾奇公式提高測井解釋符合率指明了方向。

參考文獻:

[1] Archie G E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics [J]. Transactions of the AIME, 1942, 146 (3): 54-61.

[2] Poupon A, Loy M E, Tixier M P. A Contribution to Electric Log Interpretation in Shaly Sands [J]. AIME, 1954, 201: 138-145.

[3] Simandoux P. Dielectric Measurements on Porous Media: Application to Measurements of Water Saturations: Study of the Behavior of Argillaceous Formations [J]. Revue de L’institut Francais du Petrole, 1963, 18 (Suppl 1): 193-215.

[4] 孫建孟,王克文,李 偉.測井飽和度解釋模型發展及分析[J].石油勘探與開發,2008,35(1):101-107.

Sun Jianmeng, Wang Kewen, Li Wei. Development and Analysis of Logging Saturation Interpretation Models [J]. Petroleum Exploration and Development, 2008, 35 (1): 101-107.

[5] Waxman M H, Smits L J M. Electrical Conductivities in Oil-Bearing Shaly Sands [J]. Society of Petroleum Engineering Journal, 1968, 8 (2): 107-122.

[6] 毛志強,朱衛紅,汪如軍.塔里木盆地油氣層低阻成因實驗研究(Ⅱ)[J].測井技術,1999,23(6):404-410.

Mao Zhiqiang, Zhu Weihong, Wang Rujun. Experimental Study on the Genesis of Low Resistivity Pay Zone in North Region of Tarim Basin(Ⅱ)[J]. Well Logging Technology, 1999, 23 (6): 404-410.

[7] 趙彥超,吳春萍,吳東平.致密砂巖氣層的測井評價——以鄂爾多斯盆地大牛地山西組一段氣田為例[J].地質科技情報,2003,22(4):65-70.

Zhao Yanchao, Wu Chunping, Wu Dongping. Logging Evaluation to Tight Gas Sandstone: A Case Sduty from the First Member of Shanxi Formation in Daniudi Gas Pool, Ordos Basin, China [J]. Geological Science and Technology Information, 2003, 22 (4): 65-70.

[8] 張麗華,潘保芝,李舟波,等.新三水導電模型及其在低孔低滲儲層評價中的應用[J].石油地球物理勘探,2010,45(3):431-435.

Zhang Lihua, Pan Baozhi, Li Zhoubo, et al. New Three-water Conduction Model and Its Application in Evaluation of Low Porosity and Low Permeability Reservoir [J]. Oil Geophysical Prospecting, 2010, 45 (3): 431-435.

[9] 趙彥超,周渤然.泥質砂巖的三種導電模型的研究[J].測井技術,1998,22(2):75-78.

Zhao Yanchao, Zhou Boran. Study on Three Kinds of Conductivity Models for Shaly Sand Formations [J]. Well Logging Technology, 1998, 22 (2): 75-78.

[10] 宋延杰,陳濟強,唐曉敏,等.低孔滲泥質砂巖三水孔隙結合導電模型及其在海上油田的應用[J].大慶石油學院學報,2010,34(6):106-110.

Song Yanjie, Chen Jiqiang, Tang Xiaomin, et al. Three-Water Pore Combination Conductive Model for Low Porosity and Permeability Shaly Sand and Its Application to Offshore Oilfields [J]. Journal of Daqing Petroleum Institute, 2010, 34 (6): 106-110.

[11] 張明祿,石玉江.復雜孔隙結構砂巖儲層巖電參數研究[J].測井技術,2005,29(5):446-448.

Zhang Minglu, Shi Yujiang. On Archie’s Electrical Parameters of Sandstone Reservoir with Complicated Pore Structures [J]. Well Logging Technology, 2005, 29 (5): 446-448.

[12] 鄒良志.阿爾奇公式中參數的影響因素分析[J].國外測井技術,2013,(4):23-27.

Zou Liangzhi. Influencing Factor Analysis of the Parameters in Archie Equation [J]. World Well Logging Technology, 2013, (4): 23-27.

[13] 劉之的.變m值法計算火山巖含油飽和度[J].長江大學學報:自然科學版,2010,7(3):62-65.

Liu Zhidi. Calculating Volcanic Oil Saturation by Using the Method of Variable M Value [J]. Journal of Yangtze University: Natural Science Edition, 2010, 7 (3): 62-65.

[14] 孫寶佃,張銀海,陳守軍.巖電影響因素實驗及數據處理方法[J].測井技術,2006,30(6):493-496.

Sun Baodian, Zhang Yinhai, Chen Shoujun. Core Resistivity Influence Factor Experiment and Data Processing Method [J]. Well Logging Technology, 2006, 30 (6): 493-496.

[15] 沈愛新,王 黎,陳守軍.油層低電阻率及阿爾奇公式中各參數的巖電實驗研究[J].江漢石油學院學報,2003,25(增刊上):24-25.

Shen Aixin, Wang Li, Chen Shoujun. Low Reservoir Resistivity and Litho-electric Experiment of Each Parameter in Archie Equation [J]. Journal of Jianghan Petroleum Institute, 2003, 25 (Suppl A): 24-25.

[16] 孫建國.阿爾奇(Archie)公式:提出背景與早期爭論[J].地球物理學進展,2007,22(2):472-486.

Sun Jianguo. Archie’s Formula: Historical Background and Earlier Debates [J]. Progress in Geophysics, 2007, 22 (2): 472-486.

[17] 荊萬學,陳永吉.淺探阿爾奇公式的物理學原型[J].測井技術,1997,21(4):289-291.

Jing Wanxue, Chen Yongji. On the Original Physical Model of Archie Formula [J]. Well Logging Technology, 1997, 21 (4): 289-291.

[18] Edmondson H N. Archie’s Law: Electrical Conduction in Hydrocarbon-Bearing Rock [J]. The Technical Review, 1988, 36 (4): 12-21.

[19] Serra O. Fundamentals of Well-log Interpretation-2:The Interpretation of Logging Data [J]. Journal of Petroleum Science & Engineering, 1990, 4 (2): 183-186.

[20] Ellis D V. Well Logging for Earth Scientists [J]. Journal of Petroleum Science & Engineering, 1989, 2 (4): 389-389.

[21] 何 伶,丁娛嬌,遲秀榮,等.歧口凹陷內因低電阻率油氣層飽和度定量評價方法[J].測井技術,2014,38(1):51-58.

He Ling, Ding Yujiao, Chi Xiurong, et al. On Quantitative Saturation Evaluation Method for Internal Cause Low Resistivity Reservoirs in Qikou Sag [J]. Well Logging Technology, 2014, 38 (1): 51-58.

[22] 袁 偉,張占松,呂洪志,等.水淹層混合液地層水電阻率的計算方法[J].石油天然氣學報,2014,36(9):78-83.

Yuan Wei, Zhang Zhansong, Lv Hongzhi, et al. Computation Method of Mixed Formation Water Resistivity in Water-Flooded Zone [J]. Journal of Oil and Gas Technology, 2014, 36 (9): 78-83.

[23] 韓 雙,潘保芝.復雜孔隙儲層膠結指數m的確定方法及影響因素[J].國外測井技術,2010,(1):16-19.

Han Shuang, Pan Baozhi. Determination Methods and Influencing Factors of the Cementation Index M of Complex Pore Reservoir [J]. World Well Logging Technology, 2010, (1): 16-19.

[24] 羅少成,成志剛,林偉川,等.復雜孔隙結構儲層變巖電參數飽和度模型研究[J].測井技術,2015,39(1):43-47.

Luo Shaocheng, Cheng Zhigang, Lin Weichuan, et al. Research on Saturation Model of Variable Rock-electric Parmeters for Reservoirs with Complicated Pore Structures [J]. Well Logging Technology, 2015, 39 (1): 43-47.

[25] 楊克兵,劉 歡,李士東,等.基于可動水孔隙度的巖石電阻率響應方程[J].國外測井技術,2017,38(3):22-25.

Yang Kebing, Liu Huan, Li Shidong, et al. Rock Resistivity Response Equation Based on Movable Water Porosity [J]. World Well Logging Technology, 2017, 38 (3): 22-25.

[26] 董 謙,劉小平,李武廣,等.關于頁巖含氣量確定方法的探討[J].天然氣與石油,2012,30(5):34-37.

Dong Qian, Liu Xiaoping, Li Wuguang, et al. Determination of Gas Content in Shale [J]. Natural Gas and Oil, 2012, 30 (5): 34-37.

[27] 鄧 鑫,王 鑫,劉 玥,等.核磁共振錄井發展現狀與定性識別油水層方法[J].天然氣與石油,2016,34(1):74-78.

Deng Xin, Wang Xin, Liu Yue, et al. Present Situation of Nuclear Magnetic Resonance Logging Technology Development and Qualitative Identification Method of Oil and Water Layer [J]. Natural Gas and Oil, 2016, 34 (1): 74-78.

[28] 楊克兵,袁曉紅,劉明波,等.使用電阻率比值法評價油水層的方法研究[J].天然氣勘探與開發,2015,38(1):37-39.

Yang Kebing, Yuan Xiaohong, Liu Mingbo, et al. Resistivity Ratio Method to Evaluate Oil-Water Layer [J]. Natural Gas Exploration & Development, 2015, 38 (1): 37-39.