固定舵二維修正彈外彈道仿真與動態(tài)模擬

郝永平，陳闖，張嘉易，潘雷

(1.沈陽理工大學(xué) 裝備工程學(xué)院，遼寧 沈陽 110159; 2.沈陽理工大學(xué) 機械工程學(xué)院，遼寧 沈陽 110159)

0 引言

彈道修正彈是一種具有簡易有限彈道修正能力的“簡控”彈藥，通過在普通炮射彈藥上安裝彈道修正模塊，使常規(guī)無控彈藥在飛行中能夠控制飛行軌跡，具有低成本、高精度、高效費比的優(yōu)點，深受各國軍方的青睞[1]。

固定鴨舵式二維彈道修正彈是國內(nèi)外遠(yuǎn)程精確打擊方向的研究熱點，美國軍方于2003年提出了XM1156精確制導(dǎo)組件(PGK)二維彈道修正引信[2]，通過控制修正引信的滾轉(zhuǎn)角度實現(xiàn)彈道二維修正，其精確制導(dǎo)組件就采用了鴨舵作為修正機構(gòu)。鴨舵舵面受到的氣動力用來操縱彈丸實現(xiàn)橫向和縱向修正，郝永平等[3]、朱少雄等[4]、程杰等[5-6]和紀(jì)秀玲等[7]利用數(shù)值模擬和風(fēng)洞試驗分析了固定鴨舵二維修正彈在不同馬赫數(shù)下的氣動特性，并進行了氣動力的工程建模和參數(shù)辨識。在固定鴨舵二維修正彈飛行特性方面，Wernert等[8]和Theodoulis等[9]研究了舵偏角可控修正彈的穩(wěn)定性和控制特性，許諾等[10-11]通過解析法獲得了固定鴨舵式二維彈道修正彈的非齊次攻角運動方程，并提出了一種適合固定翼雙旋彈制導(dǎo)控制研究的彈道修正新方法；王鈺等[12]基于等效力方法對修正彈側(cè)向控制力落點響應(yīng)進行了分析，丁翔洲等[13]提出了一種自適應(yīng)落點控制算法，該算法能較大幅度地提高對靜態(tài)目標(biāo)的打擊精度。目前雖然關(guān)于固定鴨舵式二維彈道修正彈的研究已經(jīng)很多，但是基于固定鴨舵高速旋轉(zhuǎn)彈的減旋控制、鴨舵測姿和不同因素干擾下全彈道飛行動態(tài)模擬等方面的研究內(nèi)容較少。

本文建立了鴨舵式二維彈道修正彈動力學(xué)模型，提出了仿真環(huán)境下二維彈道修正過程中的固定鴨舵修正機構(gòu)(以下簡稱鴨舵)減旋和測姿方法，對有橫風(fēng)和橫向跳角干擾下的橫向修正過程以及定起角干擾下的縱向修正過程進行模擬仿真，研究修正偏差值對彈道軌跡變化的影響。通過實彈射擊試驗對固定舵二維彈道修正彈在射角誤差及風(fēng)干擾下的修正能力進行研究，以檢驗鴨舵減旋和姿態(tài)監(jiān)測仿真方法的合理性。

1 固定舵二維彈道修正原理

旋轉(zhuǎn)彈丸以高轉(zhuǎn)速維持外彈道的飛行穩(wěn)定性，為了實現(xiàn)對彈丸的修正控制同時又不影響彈丸穩(wěn)定性，基于固定舵二維修正原理，設(shè)計了固定鴨舵修正機構(gòu)，該機構(gòu)與彈體之間采用軸承連接。

固定鴨舵修正機構(gòu)的模型如圖1所示，由兩對固定舵面組成：一對舵面相對于彈軸反向安裝，即為一對差動舵，兩舵面在空氣作用下沿垂直舵面的分力Fra和Frb方向相反，形成繞鴨舵轉(zhuǎn)動的導(dǎo)轉(zhuǎn)力矩Mt，使鴨舵相對于彈體反向轉(zhuǎn)動；另一對舵面相對于彈軸同向安裝，即為一對同向舵，空氣對兩舵面作用力的垂直舵面分力Fsa和Fsb方向相同，形成的合力作為鴨舵的修正力。

修正彈在發(fā)射前根據(jù)目標(biāo)位置信息在彈載計算機中裝定一個理論彈道，理論彈道是指修正彈只在減旋作用下的飛行彈道。在彈丸發(fā)射后，首先進行鴨舵減旋，即在彈丸出炮口后控制鴨舵與彈體反向低速轉(zhuǎn)動。通過地磁測量彈體的轉(zhuǎn)速、滾轉(zhuǎn)角，根據(jù)霍爾傳感器的觸發(fā)信號實時解算同向修正舵的對地角度和鴨舵的轉(zhuǎn)速。通過全球定位系統(tǒng)(GPS)信號解算彈體的位置信息，利用彈載計算機對裝定的理論彈道和GPS測定的實際彈道間偏差進行實時解算。當(dāng)彈道偏差超出設(shè)定偏差時，由指令修正模塊下達(dá)修正指令，調(diào)整鴨舵轉(zhuǎn)到修正位置，在彈丸落地之前彈載計算機一直進行上述解算。固定鴨舵式彈丸彈道修正的關(guān)鍵技術(shù)在于鴨舵的減旋控制和滾轉(zhuǎn)姿態(tài)測量。

固定鴨舵式彈道修正彈的彈道修正流程如圖2所示，彈丸發(fā)射后所有器件上電，GPS、霍爾傳感器檢測、地磁滾轉(zhuǎn)角度檢測同時進行。彈丸發(fā)射后要先進行減旋過程，首先將鴨舵的轉(zhuǎn)速控制在3～5 r/s. 此過程分別利用霍爾傳感器檢測出彈體與鴨舵的轉(zhuǎn)速差及地磁檢測出彈體的轉(zhuǎn)速，隨即解算出鴨舵的轉(zhuǎn)速。

當(dāng)GPS檢測到當(dāng)前彈道偏離目標(biāo)預(yù)定彈道時，發(fā)出指令對鴨舵進行控制，從而快速解算出需要調(diào)整脈沖寬度調(diào)制(PWM)的輸出量及輸出時間。調(diào)整之后繼續(xù)檢測彈丸是否回到預(yù)定的軌道，如果沒有，則繼續(xù)調(diào)整，如果回到預(yù)定的軌道，則繼續(xù)使鴨舵保持在設(shè)定轉(zhuǎn)速值附近勻速轉(zhuǎn)動。

2 鴨舵減旋與鴨舵測姿方法

2.1 鴨舵減旋方法

當(dāng)彈丸飛出炮口后，在空氣作用下一對差動舵片會產(chǎn)生使鴨舵反向轉(zhuǎn)動的力矩，這個力矩能使鴨舵相對彈體反向轉(zhuǎn)動，若不對鴨舵轉(zhuǎn)速進行控制，則鴨舵轉(zhuǎn)速將不斷增加[14]。因此，為了實現(xiàn)對彈道的有效修正，必須對鴨舵反轉(zhuǎn)轉(zhuǎn)速進行控制，通過電磁力矩的大小來控制鴨舵和彈體的轉(zhuǎn)速差在合理范圍內(nèi)，保持鴨舵處于微旋狀態(tài)，從而達(dá)到減旋的目的。

為了實現(xiàn)鴨舵轉(zhuǎn)速的可視化，利用Adams軟件建立了修正彈的動力學(xué)仿真模型，如圖3所示。模型包括彈體、鴨舵、參考體和大地4個部分。建立參考體的目的是為了便于觀察彈丸的飛行姿態(tài)，并將參考體與彈體通過平行副約束，參考體通過球副固定在大地上，鴨舵機構(gòu)與彈體通過旋轉(zhuǎn)副約束。

將Fluent軟件仿真獲得的彈丸和鴨舵的氣動力、力矩數(shù)據(jù)分別擬合成馬赫數(shù)、攻角的函數(shù)，并將其加在動力學(xué)模型上。通過仿真分析可知，軸承摩擦力矩Mf和電機齒槽力矩Mg與鴨舵轉(zhuǎn)速大小無關(guān)。因此可以利用(1)式實時解算修正或減旋需要的電磁力矩增量ΔMe，控制電磁力矩的大小來改變鴨舵的轉(zhuǎn)速，在控制環(huán)節(jié)中，實時解算同向舵的對地轉(zhuǎn)速、轉(zhuǎn)角，根據(jù)減旋后的轉(zhuǎn)速ω解算ΔMe的大小。

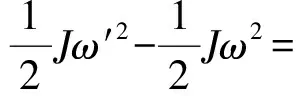
(1)

式中：J為鴨舵的轉(zhuǎn)動慣量；ω′為鴨舵初始轉(zhuǎn)速；M′e、Me分別為減旋前后的電磁力矩；θ為減旋力矩作用角度。

圖4為彈體和鴨舵轉(zhuǎn)速變化過程，彈丸出炮口后，由于空氣黏性產(chǎn)生的滾轉(zhuǎn)阻尼力矩的作用，彈丸轉(zhuǎn)速緩慢遞減。從圖4(a)中全彈道彈體和鴨舵轉(zhuǎn)速變化可以看出，彈體出炮口轉(zhuǎn)速170 r/s，經(jīng)過大約22 s飛行落地時的轉(zhuǎn)速為126 r/s，全彈道彈體轉(zhuǎn)速衰減了26.47%. 鴨舵轉(zhuǎn)速由初始時與彈體轉(zhuǎn)速大小和方向相同，在導(dǎo)轉(zhuǎn)力矩、軸承摩擦力矩和鴨舵滾轉(zhuǎn)阻尼力矩的作用下，鴨舵轉(zhuǎn)速瞬間減小并反向增加，從圖4(b)局部彈道中顯示在0.1 s時通過電磁力矩控制鴨舵轉(zhuǎn)速最終保持在8 r/s左右，落地時彈丸和鴨舵的轉(zhuǎn)速差為134 r/s，實現(xiàn)了彈丸出炮口后的鴨舵減旋控制。

2.2 鴨舵測姿方法

當(dāng)彈丸實際彈道偏離預(yù)定軌跡時，利用鴨舵停轉(zhuǎn)進行修正，因此需要確定當(dāng)前鴨舵舵片所處的滾轉(zhuǎn)位置，仿真中鴨舵滾轉(zhuǎn)測姿的示意圖如圖5所示，α為飛行中彈軸相對于地面的俯仰角。在同向舵端部處設(shè)置監(jiān)測點1和監(jiān)測點2，兩點在兩舵片處于相同位置。監(jiān)測點1、監(jiān)測點2在大地坐標(biāo)系下y值分別為y1和y2，記Dy=y1-y2，Dy的大小與鴨舵轉(zhuǎn)動情況和α有關(guān)。

以修正彈鴨舵高度45 mm、初速516 m/s、轉(zhuǎn)速170 r/s、射角45°為例，全彈道鴨舵減旋情況下的Dy及其局部變化如圖6所示。從圖6(a)可以看出，全彈道Dy的最大幅值先增大、后減小，且初始Dy的最大幅值大于彈丸落地時，在彈軸與地面平行的極短時間內(nèi)Dy幅值達(dá)到0.09 m. 圖6(b)反映了局部彈道變化。全彈道俯仰角α的變化如圖7所示。Dy的峰值隨α絕對值的減小而增大，Dy的幅值與α有關(guān)。

為了實現(xiàn)全彈道鴨舵姿態(tài)位置檢測，必須排除彈軸俯仰角變化的影響，則有Ls=Dy/cosα，即把同向舵相對于大地姿態(tài)轉(zhuǎn)化為相對于彈軸的姿態(tài)，也可看作把彈軸轉(zhuǎn)到水平面上，此時監(jiān)測的Ls最大幅值不變，全彈道Ls變化過程如圖8所示，減旋全彈道過程中Ls的最大幅值一直為0.09 m. 這樣就排除了飛行中α變化對鴨舵姿態(tài)測量的干擾。該測姿方法只能在地面模擬中采用，實際飛行中采用三軸地磁傳感器實現(xiàn)測姿。

僅測量同向舵的姿態(tài)Ls還不能滿足鴨舵滾轉(zhuǎn)一周任意角度方位監(jiān)測，其只能滿足同向舵處于豎直位置的監(jiān)測。圖9(a)為同向舵不在豎直位置的兩種情況，此時Ls1=Ls2，點1位于點2上方，F(xiàn)s1和Fs2分別為兩種情況下同向舵的受力，將力向x1軸和y1軸分解，可以看出Fs1和Fs2都有向右修的分量，同時分別有向下和向上修的分量。因此還需要測量差動舵的Lr值，如圖9(b)和圖9(c)所示。圖9(b)與圖9(c)中Ls值相同且均為正值，而Lr值大小相等、符號相反，因此依據(jù)Ls和Lr大小和符號來確定舵片所處的唯一位置。

在Adams動力學(xué)模型上設(shè)置監(jiān)測點，分別取在彈體與鴨舵相對于彈軸的相同位置。仿真測得的滾轉(zhuǎn)角如圖10所示，從圖中可以獲得彈體與鴨舵的實時滾轉(zhuǎn)角，可見減旋前鴨舵與彈體同向轉(zhuǎn)動，減旋后為反向。

3 不同因素干擾下彈道修正模擬仿真

利用第2節(jié)中的彈道修正方法，以鴨舵減旋后的彈道作為理論彈道，對各種隨機干擾因素下(橫風(fēng)、橫向跳角、定起角)的彈丸偏離進行橫向和縱向修正。

3.1 橫風(fēng)干擾下的彈道橫向修正

標(biāo)準(zhǔn)氣象條件下彈丸飛行是不受隨機風(fēng)的干擾的，然而實際環(huán)境下風(fēng)的影響是不可排除的，本文主要對橫風(fēng)干擾下彈丸的橫偏情況進行研究。修正彈的鴨舵舵高選擇為45 mm，舵偏角為4°，初速516 m/s，射角15°，轉(zhuǎn)速170 r/s，發(fā)射后鴨舵減旋控制，分別進行無風(fēng)和有風(fēng)情況的仿真。

為獲得橫風(fēng)風(fēng)速v與側(cè)向力FL的關(guān)系，利用Fluent軟件對橫風(fēng)下彈體所受側(cè)向力進行仿真。分別對舵偏角為4°、舵高分別為45 mm、50 mm、55 mm的修正彈丸進行仿真，v分別取3.4 m/s、6.8 m/s、10.2 m/s，鴨舵?zhèn)认蛄Lc和全彈側(cè)向力FLa結(jié)果如圖11所示。可以看出舵片越高，舵片受力越大，不同舵高對全彈受力無影響。

根據(jù)氣動仿真選擇橫風(fēng)對彈丸的側(cè)向作用力分別為1 N、2 N、3 N、4 N、5 N、10 N，方向向右。不同作用力下彈丸的橫偏情況如圖12所示，旋轉(zhuǎn)彈丸發(fā)射后會偏出射擊面，本文中彈丸為右旋彈，彈丸飛行中彈道會發(fā)生彎曲，最終形成橫偏。相比于無風(fēng)干擾，當(dāng)橫風(fēng)作用力從1 N增大到10 N時，橫偏增加了36.5%到298.0%.

當(dāng)彈丸初速一定、射角一定、轉(zhuǎn)速一定時，彈丸偏流可看作是確定的。而實際中由于橫風(fēng)的作用，彈丸飛行方向會受到影響，若以無風(fēng)時彈丸飛行方向為基準(zhǔn)，則有橫風(fēng)作用時彈丸會發(fā)生偏離，為了控制彈丸的方向，設(shè)定一個橫偏值，當(dāng)彈丸在橫風(fēng)作用下偏移量超過設(shè)定偏差值時，調(diào)整鴨舵姿態(tài)對彈丸飛行方向進行修正，使其圍繞著預(yù)定方向飛行。以下進行橫風(fēng)作用的仿真中，假定彈丸發(fā)射后有陣風(fēng)干擾，風(fēng)對彈丸作用力為一定值。

橫風(fēng)對彈丸的作用力取10 N，研究不同橫偏設(shè)定值對修正后彈丸橫偏軌跡的影響，修正彈道軌跡與理想彈道實時對比如圖13所示，圖中橫偏設(shè)定值Z分別選取為2 m、4 m、6 m. 3種情況分別在彈丸飛行至4.17 s、5.33 s和6.35 s時橫偏初次超過設(shè)定值，并且由于慣性橫偏值有繼續(xù)增大趨勢，此時控制鴨舵姿態(tài)，利用同向舵的修偏力改變彈丸飛行方向，此后當(dāng)橫偏值超過設(shè)定值后再次進行修正，一直修正至彈丸落地。

分析圖13中彈丸橫偏的變化規(guī)律，可以看出3種情況下全彈道的最大橫偏值分別為5.89 m、6.65 m、11.41 m，落地時的橫偏值分別為2.01 m、6.65 m、0.07 m. 相對于不修正時89.44 m的橫偏結(jié)果，修正量達(dá)到了90%左右，在給定條件下風(fēng)對彈丸的作用力為10 N、橫偏設(shè)定值為6 m時更好。

3.2 橫向跳角干擾下的彈道橫向修正

跳角是射角的組成部分，跳角可分解為橫向跳角和縱向跳角，縱向跳角在射表編擬時通常取為確定值，并稱為定起角[15]。下面對彈丸在初始向右0.5°橫向跳角下進行彈道修正，修正的橫偏設(shè)定值Z分別取2 m、5 m、10 m，彈丸橫偏的軌跡變化如圖14所示。圖14中分別給出了理論彈道、橫向跳角干擾下的無控彈道及修正彈道。

從圖14中可以看出，橫向跳角為0.5°時彈丸出炮口后橫偏變化明顯，如果不修正落點偏離達(dá)到92.01 m，無干擾下偏流為33.34 m，跳角帶來了58.67 m的橫向偏差。3種情況下修正彈丸落點偏流與無干擾位置分別相差5.27 m、0.38 m和19.79 m，修正橫偏設(shè)定值為5 m時效果最明顯。

3.3 定起角干擾下的彈道縱向修正

縱向彈道修正是對彈丸射程方向的修正，彈丸飛行中設(shè)定一個高度偏差值，當(dāng)彈丸實時偏差超出這個值時，控制鴨舵進行修正，當(dāng)修回后鴨舵停止修正，并控制鴨舵處于隨時可執(zhí)行修正的狀態(tài)，以便應(yīng)對彈丸軌跡偏差再次超出設(shè)定值。圖15為0.5°定起角下的彈道縱向修正軌跡。

從圖15中可以看出不存在跳角干擾時理論彈道下的彈丸射程為6 944.0 m，有向上0.5°跳角的無控彈道下的彈丸射程為7 067.7 m. 修正彈道為對有跳角時修正偏差值為5 m修正后的軌跡，射程為6 967.3 m. 由于向上跳角的存在，彈丸發(fā)射后高度增加，在0.62 s時高度差超出設(shè)定值，鴨舵開始修正，在4.27 s時高度差修回到5 m. 隨著修正作用的累積，高度差增速逐步減小，在9.31 s時高度差停止增加，并開始向設(shè)定值靠近，此時鴨舵仍然處于修正狀態(tài)，同向舵作用力向上，鴨舵修正至13.78 s時，完成高度差的修回。隨后彈丸在15.51 s時高度差又一次超出設(shè)定值，鴨舵進行第3次修正，直至彈丸落地。有跳角不修時相對無跳角情況射程多出123.7 m，控制鴨舵圍繞理論彈道跟隨修正，修正后射程差減小到23.3 m，大大減小了落點偏差。

4 試驗結(jié)果與分析

為了說明本文提出仿真方法的合理性，分別進行了鴨舵與彈體滾轉(zhuǎn)角的半實物仿真測量及總體修正效果的實彈射擊試驗。

4.1 鴨舵與彈體滾轉(zhuǎn)角實驗測量結(jié)果

利用地磁測試鴨舵滾轉(zhuǎn)角的實驗裝置如圖16所示，裝置由電機、聯(lián)軸器、滑環(huán)、地磁測量組件、軸承套、光電傳感器、發(fā)光元件等組成。在連續(xù)測量過程中通過滑環(huán)信號線實時讀取地磁測量解算角度值，示波器采集的地磁信號如圖17所示。通過地磁測量組件實時解算彈體對地的滾轉(zhuǎn)角。通過霍爾傳感器反饋同向舵位置脈沖，以脈沖上沿為觸發(fā)信號實時讀取當(dāng)前鴨舵滾轉(zhuǎn)角。

圖18為滾轉(zhuǎn)角的實時解算圖，其中地磁電壓信號為0.3～3.3 V，滾轉(zhuǎn)角解算包括彈體實時角度值、同向修正舵片的實時對地角度解算值，地磁實測滾轉(zhuǎn)角的誤差為4.9°. 圖18的鴨舵滾轉(zhuǎn)角解算結(jié)果與圖10仿真解算鴨舵滾轉(zhuǎn)角結(jié)果一致，說明本文提出的仿真環(huán)境下鴨舵測姿的模擬方法是合理的。

4.2 實彈射擊試驗

為了驗證固定舵二維彈道修正方法，進行了實彈射擊試驗，采用122 mm榴彈炮發(fā)射，加工3發(fā)固定舵二維彈道修正彈，由修正引信與彈體組合裝配而成的修正彈實物如圖19所示。采用高速攝影對修正彈出炮口時刻的姿態(tài)進行記錄，如圖20所示。

第1發(fā)彈用來測試鴨舵減旋后的彈道落點，即彈丸出炮口后控制鴨舵減旋，落地前鴨舵始終保持微旋狀態(tài)，驗證修正彈在鴨舵減旋狀態(tài)下彈體的飛行穩(wěn)定性及受射擊誤差影響的彈著點，第2發(fā)與第3發(fā)彈以仿真中無干擾情況下的彈道作為基準(zhǔn)，對發(fā)射跳角與氣象因素干擾下的彈道進行修正，驗證固定舵二維修正彈的修正能力。

實彈射擊試驗的結(jié)果如表1所示，試驗采用2號裝藥，表中給出了修正彈的實際射擊初速、落點位置(射程與偏流)和相對于基準(zhǔn)彈道的偏差。修正彈的落點通過雷達(dá)跟蹤測試獲取，第1發(fā)彈由于射擊誤差和橫風(fēng)、縱風(fēng)等因素的干擾，相比于基準(zhǔn)彈道，射程與偏流的偏差較大，第2發(fā)和第3發(fā)兩發(fā)彈對彈道進行了多次修正，減小了與基準(zhǔn)彈道的落點偏差，提高了打擊精度，達(dá)到了二維彈道修正彈預(yù)期的效果。試驗后對3發(fā)修正彈進行了回收，拆解后的引信體如圖21所示。

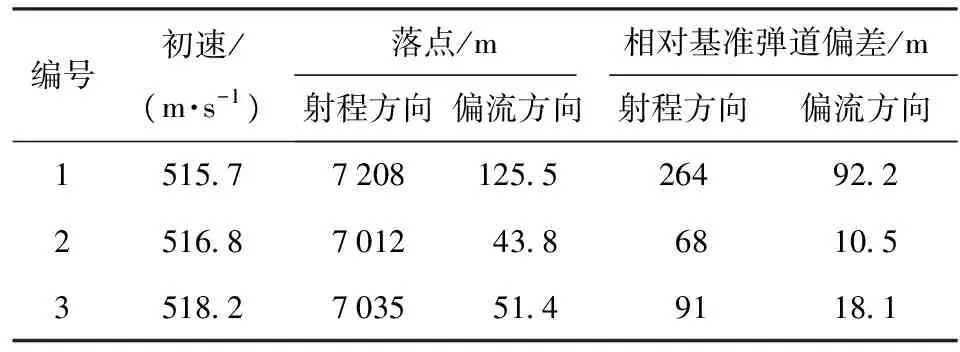
表1 試驗結(jié)果Tab.1 Experimental results

5 結(jié)論

本文建立了一種固定鴨舵式二維彈道修正彈模型，分析了二維修正原理，對二維修正彈的飛行動態(tài)與不同因素干擾下的修正過程進行仿真計算，得到結(jié)論如下：

1)仿真研究了二維修正過程中鴨舵的減旋方法和測姿方法。通過控制電磁力矩的大小來改變鴨舵的轉(zhuǎn)速，實現(xiàn)了彈丸出炮口后的鴨舵反向減旋控制；在Adams軟件中通過在同向舵與差動舵兩對舵片上建立的Marker監(jiān)測點對全彈道鴨舵姿態(tài)進行監(jiān)測，實現(xiàn)了仿真環(huán)境下對鴨舵實時滾轉(zhuǎn)角的監(jiān)測。

2)獲得了不同橫風(fēng)作用力干擾下彈丸的橫偏規(guī)律，相比于無風(fēng)干擾，當(dāng)橫風(fēng)作用力從1 N增大到10 N時，橫偏增加了36.5%到298.0%. 研究了10 N橫風(fēng)作用力下不同橫偏設(shè)定值對修正后彈丸橫偏軌跡的影響，相對于無修正情況下的橫偏，修正量達(dá)到90%.

3)分別研究了0.5°橫向跳角干擾下的彈道橫向修正和0.5°定起角干擾下的彈道縱向修正過程，通過鴨舵減旋、測姿、修正和恢復(fù)鴨舵微旋狀態(tài)的聯(lián)合控制的修正方法，能夠大大降低由跳角引起的橫向、縱向落點偏差。

4)通過半實物仿真實驗與實彈射擊試驗驗證了固定舵二維彈道修正彈鴨舵減旋與測姿仿真方法是合理的。

參考文獻(References)

[1] 鄭斌，王磊，沈衛(wèi)，等. 世界兵器發(fā)展年度報告[R]. 北京:中國兵器工業(yè)集團第210 研究所，2012.

ZHENG Bin，WANG Lei，SHEN Wei，et al. The annual report of world ordnance development[R]. Beijing: 210th Institute of the China North Industries Group Corporation，2012. (in Chinese)

[2] John G.2-D projectile trajectory corrector: US，US6502786[P]. 2003-01-07.

[3] 郝永平，孟慶宇，張嘉易. 固定翼二維彈道修正彈氣動特性分析[J]. 彈箭與制導(dǎo)學(xué)報，2012，32(3): 171-173，177.

HAO Yong-ping，MENG Qing-yu，ZHANG Jia-yi. Aerodynamic characteristic analysis on two-dimensional trajectory corrector shell with fixed-wing[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2012，32(3): 171-173，177. (in Chinese)

[4] 朱少雄，施冬梅，王毅. 固定舵二維彈道修正彈氣動特性分析[J]. 戰(zhàn)術(shù)導(dǎo)彈技術(shù)，2017(2): 41-46.

ZHU Shao-xiong，SHI Dong-mei，WANG Yi. Aerodynamic characteristic of two-dimensional trajectory correction shell with fixed-wing[J]. Tactical Missile Technology，2017(2): 41-46. (in Chinese)

[5] 程杰，于紀(jì)言，王曉鳴，等. 隔轉(zhuǎn)鴨舵式彈道修正彈氣動力工程模型與辨識[J]. 兵工學(xué)報，2014，35(10):1542-1548.

CHENG Jie，YU Ji-yan，WANG Xiao-ming，et al. Engineering modeling and identification of aerodynamics of trajectory correction projectile with decoupled canards[J]. Acta Armamentarii，2014，35(10):1542-1548. (in Chinese)

[6] Cheng J，Wang X M，Yu J Y，et al. On the response of spin stabilized projectile to side force by angular motion and impact[C]∥27th International Symposium on Ballistics. Freiburg，Germany: International Ballistics Society，2013.

[7] 紀(jì)秀玲，王海鵬，曾時明，等. 可旋轉(zhuǎn)鴨舵對旋轉(zhuǎn)彈丸縱向氣動特性的影響[J]. 北京理工大學(xué)學(xué)報，2011，31(3): 265-268.

JI Xiu-ling，WANG Hai-peng，ZENG Shi-ming，et al. CFD prediction of longitudinal aerodynamics for a spinning projectile with fixed canard[J]. Transactions of Beijing Institute of Technology，2011，31(3):265-268. (in Chinese)

[8] Wernert P. Stability analysis for canard guided dual-spin stabilized projectiles[C]∥Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit. Chicago, IL, US: AIAA，2009: 1-24.

[9] Theodoulis S，Gassmann V，Wernert P，et al. Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J]. Journal of Guidance，Control，and Dynamics，2013，36(2): 517-531.

[10] 許諾，于劍橋，王亞飛，等. 固定翼雙旋彈動力學(xué)特性分析[J]. 兵工學(xué)報，2015，36(4):602-609.

XU Nuo，YU Jian-qiao，WANG Ya-fei，et al. Analysis of dynamic characteristics of fixed-wing dual-spin projectiles[J]. Acta Armamentarii，2015，36(4): 602-609. (in Chinese)

[11] 許諾，于劍橋，王亞飛. 基于周期平均的固定翼雙旋彈彈道修正方法[J]. 航空學(xué)報，2015,36(9):2892-2899.

XU Nuo，YU Jian-qiao，WANG Ya-fei. Trajectory correcting method of fixed-canard dual-spin projectiles based on period average[J]. Acta Aeronautica et Astronautica Sinica，2015，36(9): 2892-2899. (in Chinese)

[12] 王鈺，王曉鳴，程杰，等. 基于等效力方法的雙旋彈側(cè)向控制力落點響應(yīng)[J]. 兵工學(xué)報，2016，37(8): 1379-1386.

WANG Yu，WANG Xiao-ming，CHENG Jie，et al. Analysis on impact point response of a dual-spin projectile with lateral force based on equivalent force method[J]. Acta Armamentarii，2016，37(8): 1379-1386. (in Chinese)

[13] 丁翔洲，李銀伢. 一種一維彈道修正彈自適應(yīng)落點控制算法[J]. 兵器裝備工程學(xué)報，2017，38(2): 48-52.

DING Xiang-zhou，LI Yin-ya. One dimensional trajectory correctional projectile self-adaptive impact point control algorithm[J]. Journal of Ordnance Equipment Engineering，2017,38(2): 48-52. (in Chinese)

[14] 袁備，郝永平，陶迎迎，等. 固定鴨舵高速旋轉(zhuǎn)彈修正減旋技術(shù)研究[J]. 彈箭與制導(dǎo)學(xué)報，2016，36(2): 115-118.

YUAN Bei，HAO Yong-ping，TAO Ying-ying，et al. Trajectory correction anti-rotation research of high-speed rotating projectile with fixed rudder[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2016，36(2): 115-118. (in Chinese)

[15] 韓子鵬. 彈箭外彈道學(xué)[M]. 北京: 北京理工大學(xué)出版社，2008.

HAN Zi-peng. Rocket exterior ballistic[M]. Beijing: Beijing Institute of Technology Press，2008. (in Chinese)