一題三妙解

涂 勇

(湖北省宜都市二中 443311)

在物理學習中，經常開展或嘗試“一題多解”，有助于拓寬思維、加深對知識和規律的理解，又能起到“一題多用”提高試題利用效率、走出“題海戰術”的誤區的作用.下面列舉一例，希望有拋磚引玉之效.

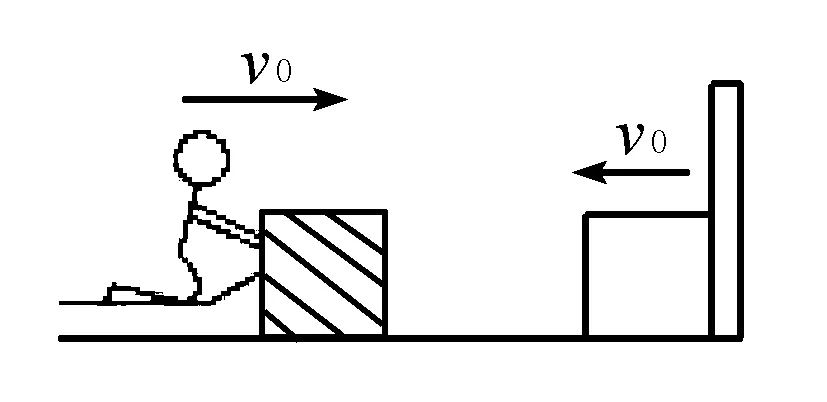
例題如圖所示，人與冰車的總質量為M，另有一質量為m的堅固木箱，M∶m=31∶2，開始時人坐在冰車上靜止于光滑水平冰面上，某時刻人將靜止的木箱以相對冰面的速度v0向右推向擋板，同時冰車反向滑動，木箱與擋板碰撞后又反向彈回，且碰撞過程無機械能的損失，人接到木箱后再以速度v0推向擋板，如此反復，求人推木箱多少次后不能再接到木箱？

分析人與冰車是一個整體，箱子與人、與擋板反復作用往返運動，情景復雜.而解力學問題可供選擇的方法有：動力學思維、能量思維和動量的思維方法；動力學思維是分析力學問題的基礎，對于復雜的力學情景，優先選擇能量或動量的方法解題.本題涉及反復推、撞的速度而不涉及位移，即不考慮作用力做功，所以選用動量的方法解題.

解法一對人、冰車和木箱系統用動量定理求解

以人、冰車和木箱系統為研究對象，系統豎直方向受力平衡，擋板對箱子的作用力即為系統外力的合力，擋板對箱子的反復碰撞，使系統動量不斷增加.取水平向左的方向為正方向，箱子每次與擋板作用，速度由-v0變為v0.

P1=0 ①

根據動量定理，箱子每次與擋板作用受沖量為：

I=mv0-m(-v0)=2mv0②

第n次推出后人車速為vn，箱子速度-v0，則人車與箱子動量的矢量和為：

Pn=Mvn-mv0③

第n次推時，箱子與擋板碰撞了(n-1)次，系統受到總沖量為：

I總=(n-1)I=2(n-1)mv0④

對系統用動量定理得:

I總=Pn-P1=Mvn-mv0⑤

設第n次推出后人不能再接到箱子，則有：

vn≥v0⑥

代入數據得：n≥8.25，取n=9，即人推出9次后，再也接不到箱子.

解法二對人、冰車和木箱系統用動量守恒定律求解

以人、冰車和木箱系統為研究對象，由于擋板對箱子的作用力為系統外力，則系統動量不守恒，如取箱子在每一次接、推前后的過程來研究，系統動量守恒，設每次推出后冰車速度分別為v1、v2、v3……vn，取水平向左為正方向，根據動量守恒定律有：

第一次推前后：0=Mv1-mv0

第二次推前后:Mv1+mv0=Mv2-mv0

同理，第三次有：Mv2+mv0=Mv3-mv0

……

第n次推前后：Mvn-1+mv0=Mvn-mv0

將各式疊加求和有：(n-1)mv0=Mvn-nmv0

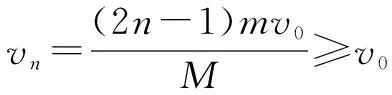
代入數據得：n≥8.25，取n=9.

解法三對人冰車整體用動量定理求解

人與冰車可視為一個物體.人每次推箱子推力的沖量為I1、I2、I3…In，總沖量I，取水平向左方向為正方向，對箱子用動量定理有:

第一次由靜止推，推力沖量：

I1=ΔP1=-mv0-0=-mv0

由于擋板將箱子彈回無能量損失，箱子彈回速度為v0，每次接推箱子，箱子的速度由v0變為-v0，所以有：

I2=ΔP2=-mv0-mv0=-2mv0

I2=I3=…=In

人推箱子n次，推力的總沖量為:I=I1+I2+I3…+In=-(2n-1)mv0

由于人推箱子的力F與箱子推人的力F′互為作用力與反作用力，即F′=-F，且兩力的作用時間相同，所以箱子對人沖量I'與人對箱子沖量I等大反向：

I′=-I=(2n-1)mv0

對于人冰車原來靜止，初動量P=0；推n次時，人車速度vn，動量P′=Mvn，根據動量定理有：

I′=P′-P=Mvn-0=(2n-1)mv0

箱子彈回時人接不到箱子的條件是：vn≥v0，代入數據解得：n=9.

評析縱觀三種解法，以系統為研究對象，動量守恒與否不是絕對的，與對應的物理過程的選取有關，靈活處理物理過程適用相應的物理規律是解題的妙之所在；動量定理多用于單一物體，對系統使用很少見，兩種用法對比出現，可開拓學生視野；其次靈活妙用數列遞推式，是解題的另一關鍵.一題多解，涵蓋了動量全章的知識和規律：沖量、動量、動量定理和動量守恒定律，復習知識訓練能力效率高.

參考文獻：

[1]人教社.高中物理人教版教課書選修3 - 5.動量守恒定律[M].北京：首付師范大學出版社，2009.