基于三維數字圖像相關法測量復合材料泊松比

，， ， ，，

(1.中國電子科技集團公司第38研究所 國家級工業設計中心，安徽 合肥 230088； 2.合肥工業大學 材料科學與工程學院，安徽 合肥 230009； 3.合肥工業大學 汽車與交通工程學院，安徽 合肥 230009)

1 前 言

玻纖增強聚合物基復合材料因高比強、高比模、低密度、抗疲勞性好等特性，廣泛用于機械承力結構件。對于前期的優化設計，往往是通過力學仿真軟件對建立的模型不斷進行模擬計算和結果比較來實現的。在此過程中，除了要明確材料的密度、彈性模量等特征參數外，泊松比也是必不可少的重要參數。它是描述材料橫向變形的彈性常數，一般是通過拉伸或壓縮的實驗方法測量獲得的。

3D-DIC是一種基于數字圖像處理技術、用于面內位移或變形的非接觸式全場光學與計算機輔助測量方法，它是根據試樣表面隨機分布的散斑場在變形前后的統計相關性來計算物體表面的位移和變形量。該法原始數據采集簡單、完整、環境適應性強，測量系統在多維度下具有很好的可調性，是現代光測力學領域一種新型高精度實驗方法。

3D-DIC方法已在眾多工程技術領域中得到了日益廣泛的應用。馬世虎、劉美華[1]等采用基于數字圖像相關計算技術的顯微數字分析系統，結合原子力顯微鏡等，實驗研究了晶態高聚物聚羥基丁酸酯(PHB)的細觀結構及對其力學性能的影響規律。朱飛鵬、雷冬[2]采用在兩個(及以上)不同位置拍攝，分別得到被測物的局部形貌，然后用3D-DIC算法計算局部坐標系之間的坐標變換關系，將局部形貌轉換至同一坐標系下并拼接得到被測物全場三維形貌，其實驗結果也驗證了該方法的可行性。曾祥福、劉程林等[3]用兩臺高速相機搭建了可用于觀測結構動態三維變形的高速數字圖像相關測量系統，在兩個動載下觀測擺錘沖擊鋁板實驗和霍普金森桿沖擊石墨圓柱實驗，得到了受沖擊鋁板的動態離面位移場演化和石墨圓柱試件橫向變形的三維位移場。潘兵、謝惠民等[4]使用兩個攝像機基于雙目立體視覺原理的三維數字圖像相關方法，對平面和曲面物體表面的三維形貌和載荷作用下的變形進行測量，并用兩個典型的實驗驗證了該方法的有效性。項大林、榮吉利等[5]搭建了三維動態DIC方法測試系統，利用沖擊加載實驗設備，對噴涂散斑的鋁靶板進行沖擊加載實驗，獲得了靶板的實時離面位移場。張賓、陳陽等[6]利用3D-DIC方法研究了水泥基材料的變形特點。

本文選用質量分數為30%的玻纖增強聚醚酰亞胺(PEI)復合材料作為測量對象，采用力學拉伸試驗和三維數字散斑光學測量系統相結合技術，采集到全部的拉伸應變數據，再通過Origin和Excel計算軟件進行分析、比較、擬合等計算處理，最后獲得該材料的泊松比。

2 實驗材料及方法

2.1 實驗設備及試樣

MTS拉伸機；PMLABDIC-3D準靜態版三維應變光學測量系統；PEI拉伸試樣(共5件，含30%玻纖)，外形尺寸參見GB/T 1040.2-2006《塑料 拉伸性能的測定》(試樣標號分別為spec1～spec5，見圖1(a)～(b))。

圖1 (a)～(b)PEI拉伸試樣及外形尺寸Fig.1 (a)～(b) PEI tensile samples and dimensions

2.2 DIC-3D 系統硬件調節與系統標定

按照常規步驟調節硬件設備，用12×9，點間距6mm的圓點標定板進行系統標定。

2.3 拉伸實驗和DIC-3D系統散斑圖像采集

DIC-3D系統圖像采集幀率為5Hz，開始采集后拉伸試樣，拉伸速率為1mm/min。

3 結果與討論

3.1 數據處理方法

根據拉伸實驗中在每次拉伸過程中下夾頭處的力、位置的原始數據，進行處理后可得到每個試樣的應力-應變曲線，同時通過比較各應力-應變曲線的吻合程度，來確定各試樣加工批次的均勻性。計算泊松比之前，先對DIC-3D系統得到的數據進行處理，可得到全場的位移和應變數據；然后根據DIC-3D系統計算得到的縱向位移場情況，將DIC-3D系統計算數據與拉伸數據同步；再根據應力-應變曲線和DIC-3D系統測量結果綜合判斷出適用于計算泊松比的時間段；最后根據此時間段內的第一、第二主應變數據得到材料的泊松比。圖2為所有拉伸試樣的應力-應變曲線總圖。

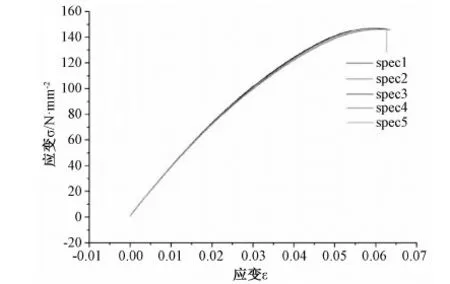
圖2 應力-應變曲線總圖σFig.2 Stress-strain curve of samples

3.2 DIC-3D系統數據處理

首先以spec1試樣的實驗數據為例，進行DIC-3D系統數據處理與分析。

相關計算區域及種子點位置如圖3所示，計算參數設置為默認值如下：網格間距：7，計算模板：29，邊界有效性：60%。

圖3 spec 1相關計算區域及種子點位置Fig.3 Correlation calculation area and seed point location of spec 1

相關計算完成后進行三維重建及應變計算，在第一幀參考圖中選擇“原點-X軸”進行坐標變換。得到以第一幀圖像中云圖區域左上端為原點，豎直向下為X軸正向(紅色箭頭方向)，水平向右為Y軸正向(綠色箭頭方向)，離面朝外為Z軸正向(藍色箭頭方向)的右手坐標系，見圖4(若要了解文中顏色，請與作者聯系)。

圖4 spec 1坐標系示意圖Fig.4 Schematic diagram of spec 1 coordinate system

觀察各階段位移場DX及數值顏色條。如圖5(a)～(b)，從階段10(文中“階段”的定義為：DIC計算得到的沿拉伸方向位移場DX結果云圖，從全場不規則的分布到沿拉伸方向位移值遞增分布的時刻)開始，X方向位移從上夾持端至下夾持端方向位移遞增，階段10即對應拉伸機開始拉伸時刻，數據同步完成。

圖5 (a)～(b)spec 1階段9和階段10的X方向全場位移云圖Fig.5 (a)-(b) Full field displacement contour of X direction of stage 9 and stage 10 for spec 1

圖6 (a)～(b)spec 1階段40應變場E1分布及E1，E2方向Fig.6 (a)-(b) Strain field E1 distribution and E1, E2 direction of stage 40 for spec 1

圖7 (a)～(b)spec 1階段951應變場E1分布及E1，E2方向Fig.7 (a)-(b) Strain field E1 distribution and E1,E2 direction of stage 951 for spec 1

觀察全場范圍內第一主應變E1和第二主應變E2及其方向，可以得到階段40至試樣斷裂前，全場第一、第二主應變方向基本一致。如圖6～7所示，選取階段40和斷裂前最后一個階段951為例，全場第一主應變方向均為縱向(右圖中紅色箭頭方向)，第二主應變方向為橫向(右圖中綠色箭頭方向)；在云圖上繪制一個矩形，并在試樣中部范圍內隨意拖動此矩形，從相關計算數據窗口可以看到矩形內E1、E2的平均值變化很小，全過程中試樣中部區域的應變場大小較均勻。

根據全場主應變情況在試樣中部選取一塊應變均勻的矩形區域，如圖8所示。

如圖9，在DIC-3D系統的分析界面，繪制全過程階段矩形內第一主應變E1平均值和第二主應變E2平均值隨階段數變化的時序曲線。橫軸代表DIC-3D系統的采集圖像序列，縱軸代表主應變大小，曲線最后的跌落是由于試樣已經斷裂。

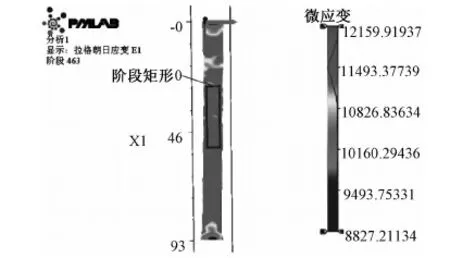
圖8 spec 1矩形區域Fig.8 Rectangular area for spec 1

將全過程每個階段該矩形區域內的第二主應變平均值E2和第一主應變平均值E1導出成excel表格，做出每個階段的|E2/E1|，再將其導入Origin中擬合出|E2/E1|隨階段數變化的時序曲線。如圖10(a)所示，可以看出，40幀之后至斷裂前這段時間的|E2/E1|數值基本上穩定在0.39，在0.40至0.38范圍內波動。

圖9 spec 1階段矩形內E1、E2平均值時序曲線Fig.9 E1 and E2 mean time series curve in the stage retange of spec1

用同樣方法對spec2～spec5進行數據處理，最后分別可以得到它們的全過程|E2/E1|時序曲線，對應如圖10(b)～(e)。

圖10 (a)spec 1全過程|E2/E1|時序曲線;(b)～(e)分別為spec 2～5全過程|E2/E1|時序曲線
Fig.10 (a) |E2/E1|time series curve of whole process for spec 1; (b) -(e)|E2/E1| time series curve of whole process for spec 2～5

可以看出，spec2和spec3在200幀之后至斷裂前這段時間的丨E2/E1丨數值基本上穩定在0.39，在0.41至0.38之間波動； spec4在55幀之后至斷裂前這段時間的丨E2/E1丨數值基本上穩定在0.40，在0.42至0.38之間波動；spec5在120幀之后至斷裂前這段時間的丨E2/E1丨數值基本上穩定在0.38，在0.39至0.36之間波動。

3.3 數據段選擇與泊松比計算

觀察圖2可以看出應變在0.05之前曲線線性都較好，選取應變0.01至0.03部分，對照拉伸原始數據表可知此段時間約為從拉伸開始第39秒至100秒，因此所有試樣都選擇該拉伸時間段的矩形區域內E1、E2平均值數據計算材料泊松比。

以spec 1 試樣為例，可使用圖5中階段205至階段510的縱軸數據，處理時重新排序為1至306。將這些數據導入到origin中擬合可得到試樣spec 1的橫向縱向應變比絕對值隨重新排序后的階段數變化的曲線，如圖11(a)所示。以此類推，可以分別得到spec 2～spec 5的橫向縱向應變比絕對值的變化曲線如圖11(b)～(e)所示。

由圖11(a)～(e)可以看出，各個試樣的橫向縱向應變比絕對值的變化在所選數據段內的變化穩定，將這些數據分別導入excel計算有效段內的|E2/E1|的平均值和方差(在10-5范圍內變化)，此時的各個|E2/E1|的平均值對應的即為該試樣的泊松比。各試樣泊松比及相應的均方差的計算結果如表1所示。再經取平均計算后，最后得到該復合材料的泊松比平均值為0.39。

表1 各試樣泊松比計算結果

圖11 (a)～(e) 分別為spec 1～5選擇數據段內橫向-縱向應變比絕對值變化曲線
Fig.11 (a)～(e) Absolute variation curves of transverse-longitudinal strain ratio in the data segment for spec 1～5

4 結 論

利用三維光學測量系統，采集玻纖增強聚醚酰亞胺復合材料在拉伸載荷作用下的形變和位移，通過選取種子點位置和計算區域、坐標系變換、|E2/E1|時序曲線模擬等數據處理，最后計算出該玻纖增強聚醚酰亞胺復合材料的泊松比為0.39，均方差值分布于10-5以內，表明3D-DIC方法適用于測量復合材料泊松比，且測量精度和可靠性較高。

[1] 馬世虎,劉美華,等.聚羥基丁酸酯球晶的微觀結構及其對力學性能的影響[J]. 材料科學與工程學報, 2007, 25(3):372～375.

[2] 朱飛鵬,雷冬. 基于三維數字圖像相關的三維形貌拼接研究[J].力學季刊, 2013, 34(3):470～474.

[3] 曾祥福,劉程林,馬少鵬. 高速三維數字圖像相關系統及其動載三維變形測量[J]. 北京理工大學學報, 2012, 32(4):364～369.

[4] 潘兵,謝惠民,李艷杰. 用于物體表面形貌和變形測量的三維數字圖像相關方法[J].實驗力學, 2007, 22(6):556～567.

[5] 項大林,榮吉利,等. 基于三維數字圖像相關方法的水下沖擊載荷作用下鋁板動力學響應研究[J].兵工學報, 2014, 35(8):1210～1217.

[6] 張賓,陳陽,等. 三維數字圖像相關法及其在水泥基材料變形研究中的應用[J].電子顯微學報, 2015, 34(6): 521～549.