基于優勢關系的多屬性群決策方法

林偉華，李進金，吳宇寧

LIN Weihua1，2,LI Jinjin2,WU Yuning1，3

1.福建師范大學 數學與計算機科學學院，福州 350108

2.閩南師范大學 數學與統計學院，福建 漳州 363000

3.莆田學院 基礎教育學院，福建 莆田 351100

1.College of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350108,China

2.College of Mathematics and Statistics,Minnan Normal University,Zhangzhou,Fujian 363000,China

3.College of Basic Education,Putian University,Putian,Fujian 351100,China

1 引言

多屬性群決策是群體決策和多屬性決策的一個交叉研究方向，是現代決策理論的重要組成部分，由于具有客觀理性、集思廣益、可最大程度減少決策中不合理因素等特點，其理論與方法在科技、工程、政治、軍事、經濟和管理等領域得到廣泛應用[1]。因此，多屬性群決策問題的相關研究具有重要的現實意義和一定的實用價值。近年來，經過國內外學者的不懈努力，多屬性群決策問題取得了一定的發展，目前主要用于解決有限方案中具有多個屬性（或評價指標）的排序和優選問題[2-4]。粗糙集理論[5]最早于1982年由波蘭科學家Z.Pawlak提出，由于其無需借助任何先驗知識，能通過對現在數據的有效分析與推理，揭示數據的潛在規律，在知識發現、模式識別、機器學習、數據挖掘等領域得到廣泛應用[6-8]。

由于多屬性群決策理論中的決策矩陣描述類同粗糙集中的信息系統描述相類似，故利用粗糙集理論來研究多屬性決策問題儼然成為當今決策分析領域中一個新的研究方向。截止目前，基于粗糙集的多屬性決策[9-17]主要有排序決策和分級決策這兩類。其中，分級決策的主要方法是：在優勢粗糙集模型中，提取信息系統中的分級決策規則、并在群決策環境中研究分級規則選擇及其融合問題。排序決策主要先利用熵方法與屬性重要度的計算求得屬性權重，再集結決策矩陣中的判斷得到整體方案的排序，這種方法主要用于群決策及多屬性決策中排序決策問題解決。通常，在基于粗糙集的多屬性群決策排序模型中，都直接集結專家給出的決策判斷矩陣得到排序結果，很少考慮其決策屬性。然而，在一些實際決策問題中，專家可能既給出每個對象的屬性評價值，又對其進行初步分級決策，在這種情況下，最終決策應集結屬性評分信息和初步決策信息得出其排序。而這種集結排序的核心就是屬性權重的設定，因為在多屬性群決策問題中，不同的專家權重或屬性權重均會導致不一樣的評價結果。

優勢關系是粗糙集中用于描述信息系統上優劣關系的一種刻畫。在決策問題中，利用優勢關系方法獲得的規則與利用粗糙集方法獲得的決策規則一致，而且用優勢關系方法能對所有屬性的取值都給出決策結果[18]。在現有的多屬性群決策研究模型基礎上考慮專家的初步決策，給出一種新的基于優勢關系的多屬性群決策的模型描述：在信息系統中，先通過計算條件屬性和決策屬性的優勢粒結構相似度，得到條件屬性在決策中的重要度，依此確定條件屬性在專家評價中所占的權重；再通過計算專家三支決策判斷的優勢粒結構之間的相似度，得到專家與專家群體之間的共識度（即認可度），選共識度最高的專家為群體評價的代表；最后由專家群體代表與其他專家之間的相似度來確定其他幾位專家的權重，具體計算方法在第2章中給出。

2 基于優勢關系的多屬性群決策方法

為了便于理解，先作粗糙集理論的相關基本概念介紹。

定義1[18]設(K,≤)滿足以下性質。

（1）自反性：x≤x(x∈K)；

（2）反對稱性：當 x≤y，y≤x時，x=y(x,y∈K)；

（3）傳遞性：當 x≤y，y≤z時，x≤z(x,y,z∈K)；稱(K,≤)為偏序集。若進一步有?x,y∈K，且 x≤y或x≤y，則(K,≤)是全序集。

定義2[18]設(U,A,F)是連續值信息系統，其中U={x1,x2,…,xn}為對象集，A={a1,a2,…,am}為屬性集，F={fl:U→Vl(l≤m)}為對象與屬性之間的關系集，Vl為屬性al的有限值域。對于任意屬性集B?A，記，稱為連續值信息系統(U,A,F)上的優勢關系，(xi,xj)∈表示對象xj在屬性集B上優于對象xi。

定義3[18]記，則表示在屬性集B條件下，優于對象xi的所有對象集合，稱為xi的優勢類。

2.1 優勢粒結構及其相似度

多屬性群決策問題的實質是利用群體專家對評價屬性及決策屬性給出的評判信息，通過一定方法對待選的方案進行全面分析、合理排序、選擇最優及綜合評價，以找到一種便捷的排序方法。基于此，本文借鑒粗糙集優勢關系與屬性聯系度等有關知識，將優勢關系引入多屬性群決策的對象排序問題，并提出了基于優勢關系的多屬性群決策排序方法。

多屬性群決策問題中，為了對各屬性進行關系分析，先引入優勢粒結構的定義，并研究優勢粒結構相似度的定義及其相關性質。

定義4設U={x1,x2,…,xn}為非空論域，≤B為U上的優勢關系，定義為論域U在≤B下的優勢粒結構。

定義5設U={x1,x2,…,xn}為非空論域，B是U上所有優勢關系構成的集合，任意的≤B1,≤B2∈B，是其相應的優勢粒結構。定義之間的相似度

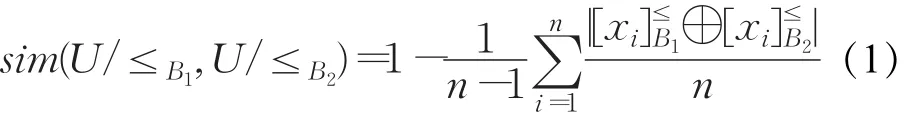
式中⊕為集合的對稱差運算，為方便，將sim(U/≤B1,U/≤B2)簡記為 sim(≤B1,≤B2)。

性質1 任意的≤B1,≤B2∈B，有0≤sim(≤B1,≤B2)≤1。特別的，若≤B1=≤B2，則 sim(≤B1,≤B2)=1。

證明（1）由于≤B1,≤B2具有自反性，所以對?xi∈U，，因此故

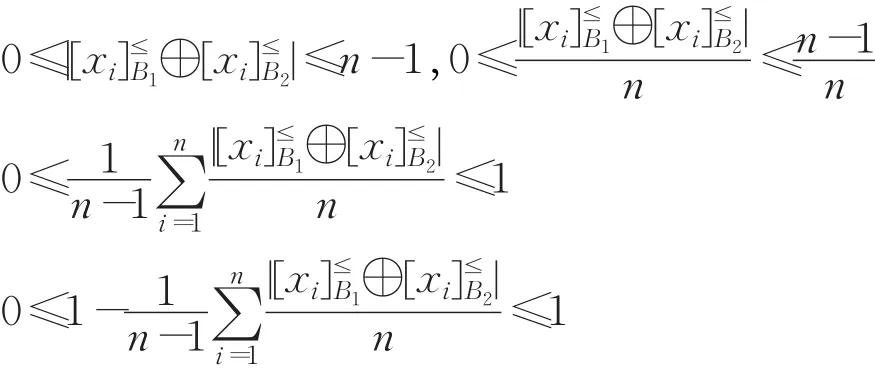
（2）特別的，?xi∈U ，因為。所以，則，所以

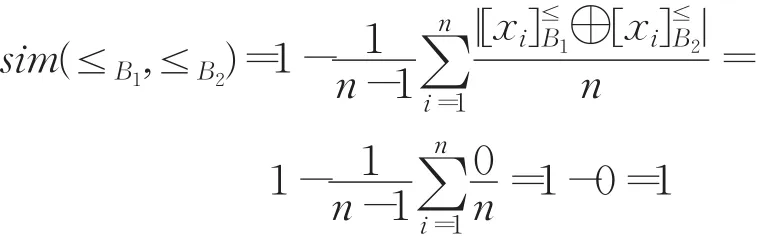
性質2 設U={x1,x2,…,xn}(n≥2)，≤B1,≤B2∈B ，其中≤B1:x1≤B1x2≤B1…≤B1xn，≤B2是≤B1的逆關系，即≤B2:xn≤B2xn-1≤B2…≤B2x1，則 sim(≤B1,≤B2)=0。

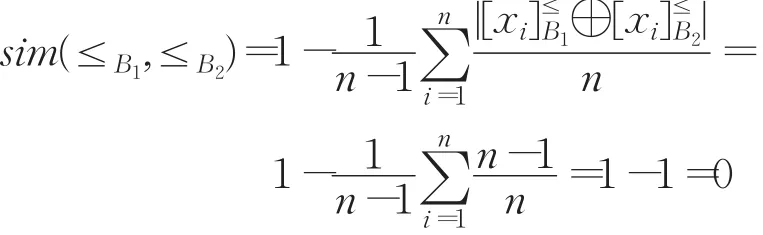
性質2表明，當兩個優勢關系完全相反時，它們的相似度達到最小值0。

性質3設，U={x1,x2,…,xn}(n≥2)，I是U上的恒等關系，E是U上的全域關系，兩者均是偏序關系，則sim(I,E)=0。

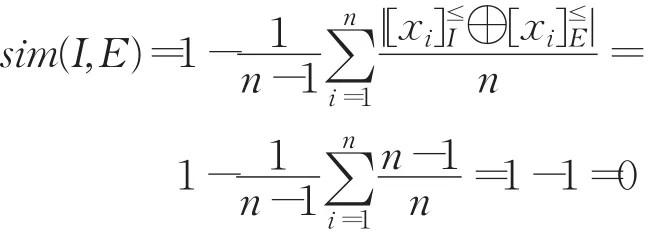
從優勢關系來看，全域關系隱含著U上任意兩個對象都是可比較關系，而恒等關系則表示任意兩個不同對象都是不可比較關系。由此可以判斷，這兩種關系的相似度達到最小值0。性質3恰好驗證了這一點。

性質 4 設 U={x1,x2,…,xn}(n≥2)，≤B1:x1≤B1x2≤B1…≤B1xt≤B1xt+1≤B1…≤B1xn，將 xt與 xt+1的位置互換得到≤B2:x1≤B2x2≤B2…≤B2xt+1≤B2xt≤B2…≤B2xn,1 ≤t≤n-1，則sim(≤B1,≤B2)=1-2/n(n-1)(n≥2)。

證明由已知≤B1:x1≤B1x2≤B1…≤B1xt≤B1xt+1≤B1…≤B1xn，≤B2:x1≤B2x2≤B2…≤B2xt+1≤B2xt≤B2…≤B2xn，易得通過計算，得到。而當i≠t,t+1時因此有時。故有

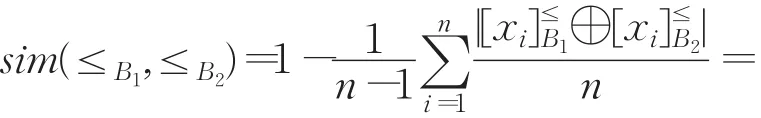
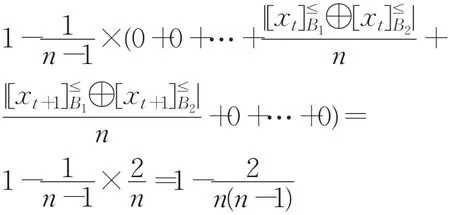
從性質4可以看出，當n值較小，例如當n=2時，交換相鄰兩個對象位置后，得到這兩個優勢粒結構的相似度取到最小值0；當n取值較大時，交換相鄰對象位置后得到的優勢粒結構的相似度比較大。

2.2 權重的確定

2.2.1 屬性權重的確定

作為影響決策結果準確性的核心—屬性的權重系數反映了屬性間的相對重要性，因此屬性權重系數的確定成了國內外學者的研究熱點，目前研究方法主要有層次分析法、模糊綜合評價法和德爾菲法等。在多屬性決策問題里，對象在各屬性的取值均為有序的，對于數值型的屬性取值，取值上的不小于就是一個預序；對于語言值的屬性取值，規定的不劣于關系亦是一個優勢關系；對于區間型或集值型的屬性取值，也可以通過合理定義得到相對應的優勢關系[19-20]。

在多屬性群決策模型中，設Sk=(U,A?g0gggggg,fk)為專家ek(k=1,2,…,T)的決策系統，記，對于屬性集 A={a1,a2,…,am}，任意的aj∈A，則aj在決策系統S中確定的不劣于關系定義為≤aj={(xi1,xi2)|f(bi1,aj)不劣于 f(bi2,aj)}，d在決策系統S中確定的不劣于關系定義為≤d={(ai1,ai2)|di1≥di2}。如果≤aj同≤d優勢粒結構的相似度較小，則屬性aj在決策系統中的權重較小，反之則較大。

本文由優勢關系誘導出優勢粒結構，通過屬性之間優勢粒結構相似度的大小，得到決策系統中屬性權重大小的關系分析，進而得到以下加權方法。

定義6屬性aj∈A在系統S中的權重ωj

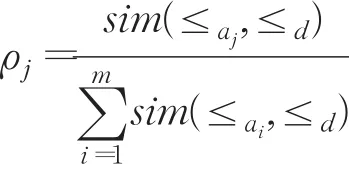
2.2.2 專家權重的確定

目前對專家權重的設定大多根據專家的專業背景、對決策問題的熟悉程度、知名度、能力水平等因素來確定，或是根據專家間的相互評價結果來確定。在實際問題中，專家決策的可信度除了考慮這些因素外，還應考慮專家個人評價結果與其他專家評價結果的相互關系，這種由專家評價結果的相互關系決定產生的權重是一種客觀權重，在實際應用中可單獨使用，也可和主觀權重結合使用。

考慮專家在決策屬性下給出的評判結果，根據拒絕評判決策、延遲評判決策和接受評判決策對象集定義專家評價的相似度，分析專家之間評判結果的關系。

定義7設E={e1,e2,…,eT}為專家群體，根據各個專家給出的決策系統Sk=(U,C?g0gggggg,fk)，定義專家ek1和ek2評價的相似度為：

定義8[19]設E={e1,e2,…,eT}為專家群體，定義專家ek在群體中的共識程度為：

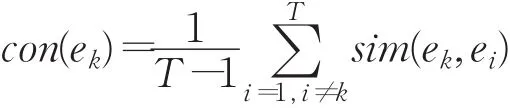
定義9[19]設E={e1,e2,…,eT}為專家群體，若con(e*)=，則稱e*為專家群體中的代表專家。

通過專家間的評價相似度定義各專家在群體中的共識程度，規定群體共識程度最高的專家為代表專家（記為e*），各專家在群體評價中的共識程度用其與專家e*的相似度近似計算，依此定義各專家的權重向量。

定義10專家ek和專家群體評價的共識程度用sim(ek,e*)來近似計算，專家ek的權重ωk[13]設定為：

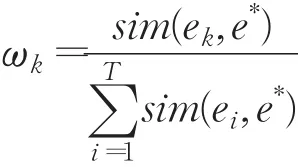
3 基于優勢關系的多屬性群決策方法的應用

3.1 實例背景介紹

參照文獻[21]表9.4，將專家初評結果整理得到表1，設3位面試專家為ej(j=1,2,3)，10名應聘人員為xi(i=1,2,…,10)，應聘者工作能力3個評價指標（屬性）分別為專業能力a1，語言表達能力a2，團隊協作能力a3，決策屬性d作出粗粒度的三支決策“通過”（記作“2”）、“不通過”（記作“0”）、“延遲決定”（記作“1”）的判斷。為簡單起見，在計算時分別用{2，1，0}來代替應聘者工作能力3個評價屬性a1，a2，a3的語言值{好，中，差}。

表1 某企業招聘面試專家初評結果表

3.2 評價步驟及計算結果

3.2.1 計算屬性的權重

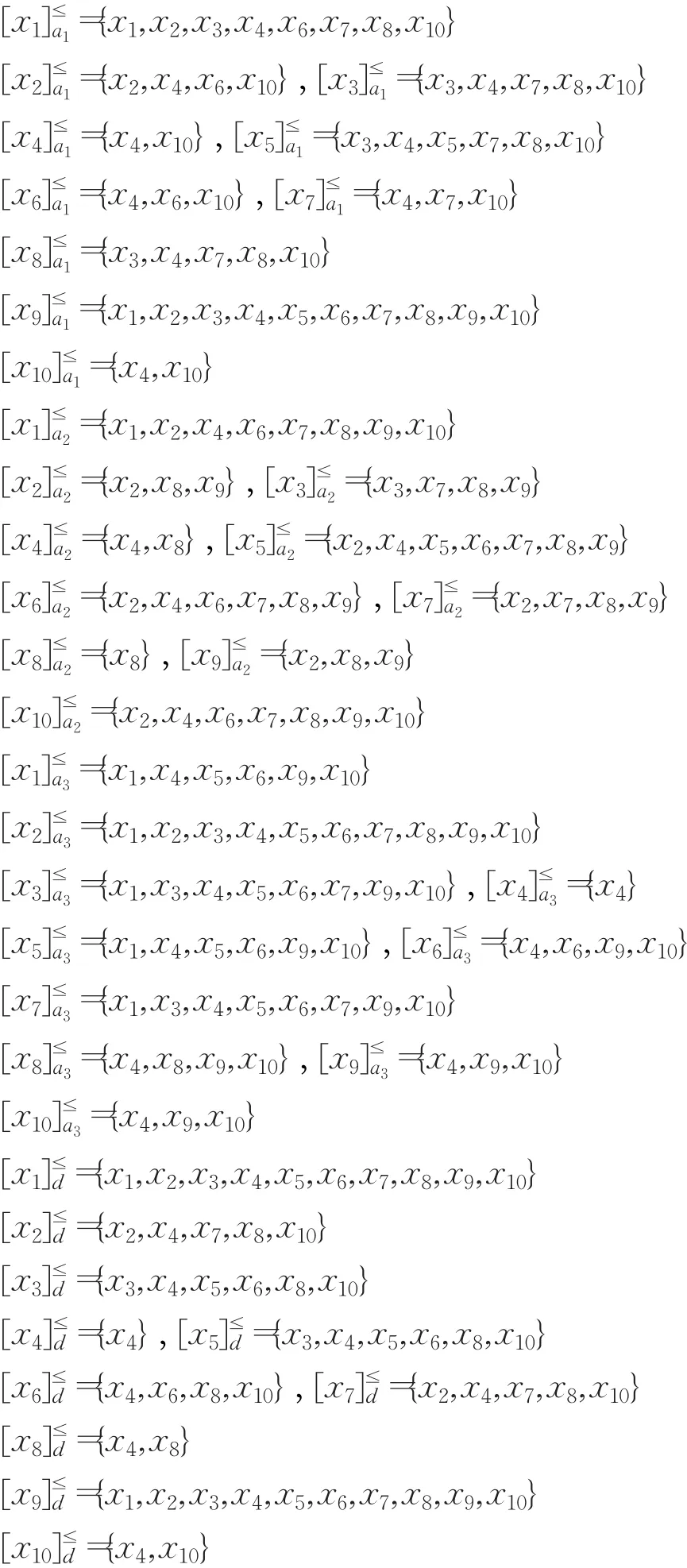
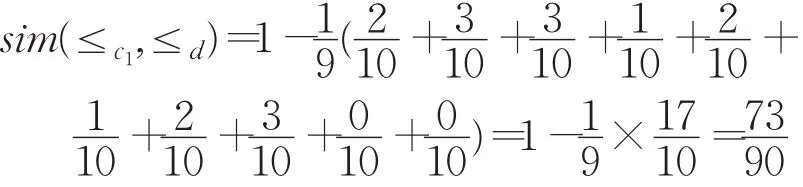
同理計算可得：

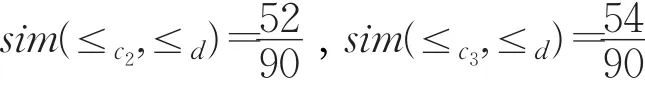
得到：

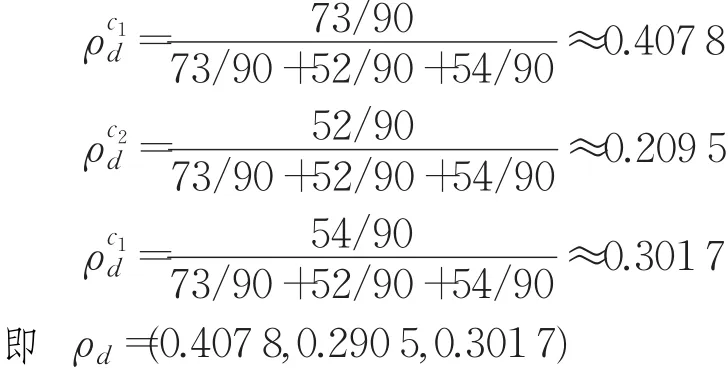
由ρd的計算結果可得，綜合3位專家的評判結果，3個評價指標（屬性）的重要程度依次為專業知識、團隊協作能力、語言表達能力。

3.2.2 計算專家的權重

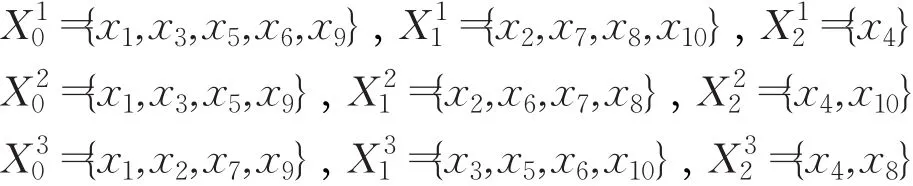
由式（2）計算可得：

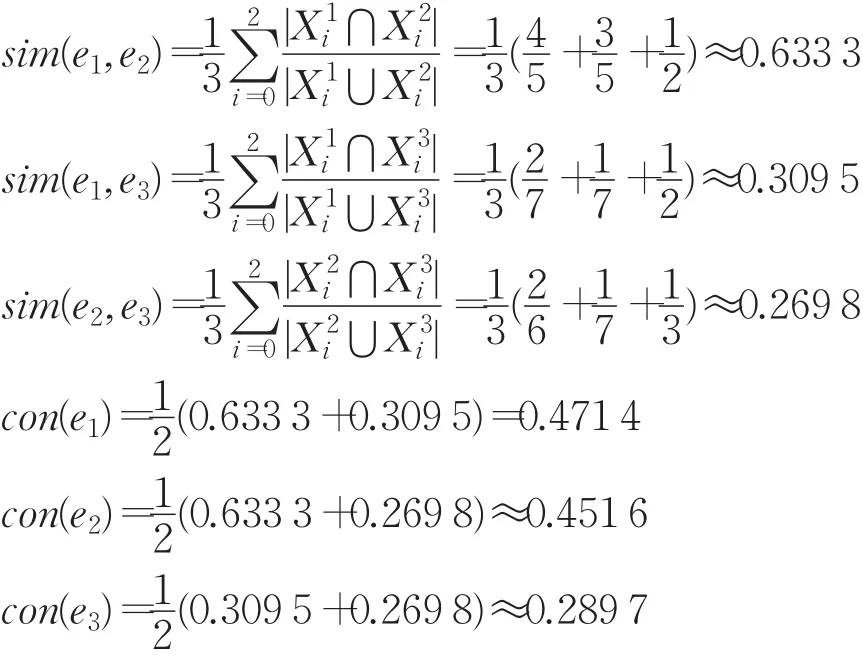
因為 con(e1)＞con(e2)，con(e1)＞con(e3)，故選擇 e1為3位專家中的代表專家。各專家的權重計算如下：

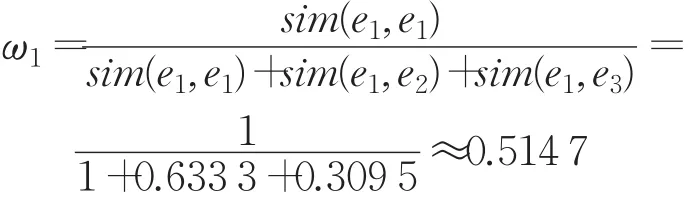
同理，計算得到：

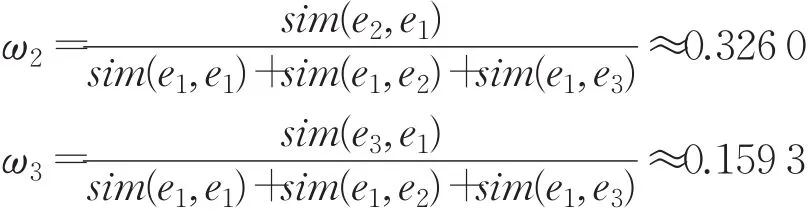
3.2.3 集結群決策的結果

為方便計算，用{0，1，2}的數值標度，分別代表評價結果{差，中，好}的語言值，先考慮對屬性權重進行集結得到表2。

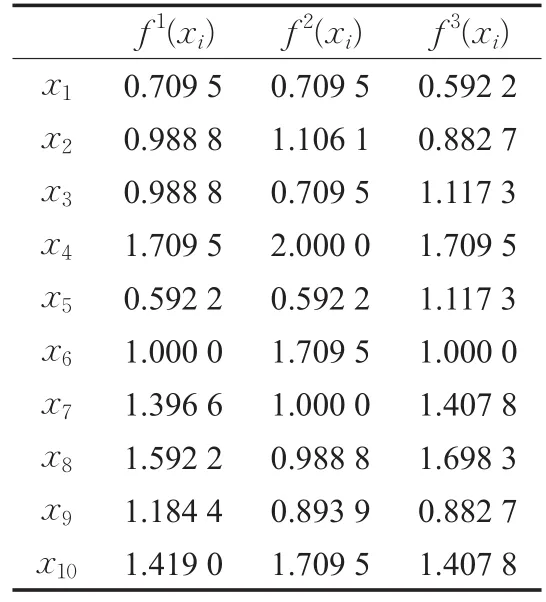
表2 各專家綜合評價結果

結合各專家的權重進一步集結，得到：

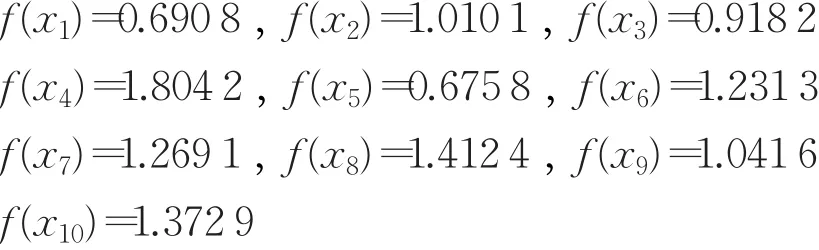
于是，由最后計算結果得到10名面試人員的綜合能力排名為：

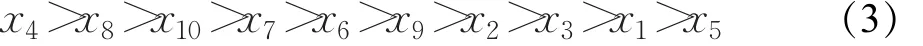
式（3）的計算結果與文獻[21]中的結論x4＞x8＞x10＞x7＞x6＞x9＞x2＞x3＞x5＞x1基本一致。

4 結論

在現有的多屬性群決策模型研究基礎上，文章同時考慮評價專家做出的初步決策信息，提出基于粗糙集優勢關系的多屬性群決策模型，該模型考慮了專家對研究對象做出的粗粒度評價信息，具體表現在：先利用優勢關系法描述了專家初步分級決策的信息結構，接著定義了專家初步分級評價的相似度，并依據給出的決策表客觀確定了各專家評價的權重；同時，該模型也定義了優勢粒結構相似度并研究其相關性質，這種基于優勢粒結構相似度的計算方法能夠直觀性地解釋屬性的客觀權重。最后，通過實例對帶有三支決策的專家評價方案進行數據處理，分別得到面試者工作能力各個評價指標（屬性）和面試專家的權重分配，對其進行集結得到的最終評價結果與文獻[21]的結論基本一致，這也說明了該方法的可行性與有效性。與文獻[21]中基于粗糙集的細粒度決策模型相比較，文章建立的基于優勢關系的粗粒度多屬性群決策方法起到異曲同工之效，但其在計算過程上相對簡潔，這為今后建立多粒度決策模型粒度粗細的選擇提供了一定的參考價值。由于篇幅有限，在后續研究中，將進一步考慮該方法在一些真實數據上的實驗操作，并對實驗結果做出詳細的分析。

參考文獻：

[1]Yue Z.A method for group decision-making based on determining weights of decision makers using TOPSI[J].Applied Mathematical Modelling，2011，35（4）：1926-1936.

[2]Wang W，Liu X，Qin Y.Multi-attribute group decision making models under interval type-2 fuzzy environment[J].Knowledge-Based Systems，2012，30：121-128.

[3]Chen Z，Yang W.A new multiple attribute group decision making method in intuitionistic fuzzy setting[J].Applied Mathematical Modelling，2011，35（9）：4424-4437.

[4]Jiménez A，Mateos A，Sabio P.Dominance intensity measure within fuzzy weight oriented MAUT：An application[J].Omega，2013，41（2）：397-405.

[5]Pawlak Z.Rough set[J].International Journal of Computer&Information Sciences，1982，11（5）：341-356.

[6]Xu W，Li W，Luo S.Knowledge reductions in generalized approximation space over two universes based on evidence theory[J].Journal of Intelligent&Fuzzy Systems，2015，28（6）：2471-2480.

[7]Jiye Liang，Yuhua Qian，Deyu Li，et al.Theory and method of granular computing for big data discovery[J].Science in China-Series E：Information Sciences，2015，45（11）：1355-1369.

[8]Wu W Z，Leung Y.Optimal scale selection for multi-scale decision tables[J].International Journal of Approximate Reasoning，2013，54（8）：1107-1129.

[9]張文修，梁怡，吳偉志.信息系統與知識發現[M].北京：科學出版社，2003.

[10]Qian Y H，Liang J Y，Song P，et al.On dominance relations in disjunctive set-valued ordered information systems[J].International Journal of Information Technology&Decision Making，2010，9（1）：9-33.

[11]Huang B，Wei D K，Li H X，et al.Using a rough set model to extract rules in dominance-based interval-valued intuitionistic fuzzy information systems[J].Information Sciences，2013，221：215-229.

[12]Zhang H Y，Leung Y，Zhou L.Variable-precision-dominance-based rough set approach to interval-valued information systems[J].Information Sciences，2013，244：75-91.

[13]Xu W，Sun W，Zhang X，et al.Multiple granulation rough set approach to ordered information systems[J].International Journal of General Systems，2012，41（5）：475-501.

[14]Song P，Liang J，Qian Y.A two-grade approach to ranking interval data[J].Knowledge-Based Systems，2012，27：234-244.

[15]Liang D，Liu D.A novel risk decision making based on decision-theoretic rough sets under hesitant fuzzy information[J].IEEE Transactions on Fuzzy Systems，2015，23（2）：237-247.

[16]Sun B，Ma W.Rough approximation of a preference relation by multi-decision dominance for a multi-agent conflict analysis problem[J].Information Sciences，2015，315：39-53.

[17]Chakhar S，Ishizaka A，Labib A，et al.Dominance-based rough set approach for group decisions[J].European Journal of Operational Research，2016，251（1）：206-224.

[18]張文修，仇國芳.基于粗糙集的不確定決策[M].北京：清華大學出版社，2005：113-116.

[19]Wang H，Guan Y，Huang J，et al.Decision rules acquisition for inconsistent disjunctive set-valued ordered decision information systems[J].Mathematical Problems in Engineering，2015，2015：1-8.

[20]Hakimi A A，Furberg H，Zabor E C，et al.An epidemiologic and genomic investigation into the obesity paradox in renal cell carcinoma[J].Journal of the National Cancer Institute，2013，105（24）：1862-1870.

[21]賈修一，商琳，周獻中，等.三支決策理論與應用[M].南京：南京大學出版社，2012.