最小偏差法船舶調度

林 輝， 陳順懷

(武漢理工大學 a.交通學院, b.高性能船舶技術教育部重點實驗室， 湖北 武漢 430063)

0 引 言

在世界海洋運輸業迅速發展的今天，船舶調度作為港口調度的關鍵內容之一，從20世紀50年代開始就引起了許多學者的關注。船舶調度是一種能降低船務公司營運成本的手段。船舶調度方案的優劣直接關系到船舶航運過程中的船舶運輸效率、油耗情況以及港口成本等諸多經濟效益的好壞，從而對航運公司的盈利能力產生實質性的影響，因此對配船方案的優化就顯得尤為重要。配船方案的優化過程涉及諸多問題，比如船舶運輸成本的構成、客流量的滿足、船舶速度和航行時間的匹配等。因此，船舶調度優化是一個多目標優化問題。

每條航線的配船方案和調度是由船務公司的專門調度人員負責安排的。一般來說，在船舶調度中所考慮的問題有許多是隨機可變的，比如本文所討論的客船調度，除淡季和旺季的客流量差異以外，其每日的客流量也是隨機變化的，還有水域、天氣條件也會有所差異。這些都成為影響船舶調度方案優劣的約束條件。

現今，絕大多數船舶(包括集裝箱船、散貨船、客船)的配船主要還是依靠專門調度人員的經驗，以至于現有的船舶運輸資源未得到充分的利用，從而導致運輸成本相對較高，并且不能較好地滿足客戶的需求。因此，采用合適的方法對該問題進行優化處理非常重要。目前，已有許多學者采用蟻群算法等相關算法進行求解優化，本文在其后也對其進行了一些比較。

1 遺傳算法及最小偏差法簡介

1.1 遺傳算法及其基本理論

遺傳算法(Genetic Algorithm，GA)是一種自適應全局優化搜索算法。它主要借鑒生物在繁殖生存過程中的遺傳和進化規律。早在20世紀60年代, HOLLAND就提出GA算法的理論;20世紀70年代， JONG首次根據GA理論開展計算機數值試驗；20世紀80年代， GOLDBERG對之前學者所做的理論和試驗研究進行總結歸納得到現今的經典遺傳算法。

GA是一種傳統的智能算法，它有良好的隨機性和全局性，是一種高效的、并行的、全局性的成熟優化方法。經典遺傳算法的優化變量是采用二進制碼來描述的，多個優化變量的二進制碼串接在一起形成一組染色體，這種編碼方式既適用于變異操作，又可對其進行交叉操作。在創建初始種群時，代表個體的二進制串是在一定字長的限制下隨機產生的。GA算法中的交叉算子其主要功能是交叉2條染色體，交叉位置是隨機產生的，染色體的交叉位置也是隨機選取的，從而保證后代的隨機性，2個染色體在進行隨機交叉后，其對應位置的二進制碼將進行交換并生成新的2個染色體。變異算子作用在單一染色體上，通過1個隨機概率對單個染色體上的二進制碼進行變異，即將“0”變異成“1”，或者將“1”變異成“0”，從而得到新的染色體。最后將這些不斷交叉變異的個體代入適應度函數進行計算，比較適應度值之間的差異是否滿足精度要求，滿足精度要求即可獲得全局最優解。

1.2 最小偏差法

在實際的多目標尋優過程中，由于約束條件和優化目標較多，往往很難求得最優解，故在工程應用中主要以尋找多目標優化中的滿意解為最終優化目標。本文采用的最小偏差法就是一種可用于多目標問題優化的決策方法。

常見的多目標優化模型可以表示為

x∈Rn(1)

式中：f1(x),f2(x),…，fl(x)為l個極小化目標函數；fl+1(x),fl+2(x),…，fm(x) 為m-l個極大化目標函數；gj為線性、非線性不等式函數式；hk為線性、非線性等式函數式；j為不等式約束編號，其值為1，2,3，…；k為等式約束編號，其值為1,2,3，…；x為決策變量，x=(xl,x2,…，xn)T。

多目標優化問題的核心思想是將多個適應度函數同時求取最優解，但是由于不同適應度函數的最優解必然是不同的值，故而在多目標優化問題中引入較優解的概念,即多個適應度函數在較優解的情況下，可同時獲得相對較優的適應度值。1951年，TKOOPMANS提出一種與較優解概念相同的有效解概念，被稱之為Pareto最優解。Pareto最優解是通過對多個適應度函數構成的向量函數的適應度值進行大小比較獲得的。

假設X?Rn是多目標優化問題的約束集，若x*∈X，且不存在x∈X使得?i∈(1,2,…,l),fi(x)≤fi(x*)，而對于?i∈(l+1,l+2,…,m),fi(x)≥fi(x*)，則稱x*為其有效解[4-5]。

對于多目標優化問題，主要工作就是尋找合適的方法來獲得目標的Pareto最優解，因此，尋找一種合適的決策函數來處理多個適應度函數，使其能進行相互比較就成了關鍵性問題。如式(2)所示，可以通過一定的權重策略將m個函數式構成1個以x為自變量的復合函數式：

F′(x)=F′(f1(x),f2(x),…，fm(x))(2)

對式(2)中多個適應度函數共同優化問題的解是一個解集，即不只存在一個解，不同的決策方法和求解算法獲得的解不盡相同，其具有的意義也存在差異，本文采用最小偏差法[5-6]作為統一適應度函數的決策方法：

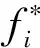
2 船隊調度優化模型的構建

本文主要以迅隆公司的船舶調度案例為基礎，結合其公司船舶數量、航線情況和航班要求等基礎條件建立數學模型。

迅隆公司擁有6艘客船構成的船隊，將這6艘客船分別命名為迅隆1～6號。船型的不同導致每條船的載客人數和每公里耗油都有差異，此外所需船員人數也不同。船隊航行的航線主要有4條，分別是蛇口-中環、蛇口-澳門、蛇口-機場和福永-澳門。耗油量的不同可能由航線里程和水域狀況的不同導致，不同船型的噸位不同導致其在港口的停泊、服務等綜合費用也存在較大的差異[8]。

2.1 航運成本組成部分

耗油量：不同船舶的主機在不同單位時間和單位里程的油耗存在較大差異。本文按如下的公式計算主機在船舶往返航班中的油耗成本：

往返航班油耗成本=往返航班里程×

油耗×單位油價 (4)

人員工資：出航的工作人員除了有基本的工資、伙食補貼之外，還有按出勤天數計算的獎金。本文通過相關薪資數據，按如下公式計算船員的航行補貼：

航行補貼=航班數×基本航線補貼×航線系數 (5)

港口費用：由于不同噸位的船舶在不同的港口收費標準存在差異，故必須根據碼頭的實際情況獲取港口費用。

2.2 目標函數

2.2.1 總成本最小化

該優化模型以船舶日總成本費用最小化為目標構建優化模型，其中包括成本、碼頭綜合管理費用和船員津貼成本(船員工資為固定成本，此處不作考慮)。

(1) 船舶油耗成本。不同船型的船舶在不同航線上由于主機油耗和航程的不同，成本也不盡相同，此處令不同船舶在不同航班上的油耗成本為oij，則

oij=xij×cij(6)

式中：xij為船舶i開往往返航班j的次數，xij∈(0,1)。它是模型的0-1變量，決定了本研究所建立的數學模型將是0-1整數規劃。具體含義如下：

(8)

式中：cij為船舶i開往往返航班j的耗油量；Pf為單位油價；i為船舶編號，i=1,2,3,…,M，M為船舶數量;j為往返航班編號，j=1,2,3,…,N，N為航班數量。

(2) 船舶碼頭管理綜合費用。由船舶i在往返航班j中的碼頭使用費用Wij得到1天中所有航班所需要的碼頭總費用為

“張勇說得已經非常直白，花如此巨資直接收購而不是戰略投資餓了么，說明餓了么對于阿里未來發展之重要性，就是成為新零售戰略的重要力量。”何軍向《中國儲運》雜志記者闡述了自己的觀點。

(9)

式中：Po為1天中所有航班所需碼頭費用；Wij為船舶i在往返班j中的碼頭使用費。

(3) 船員工資。針對人員薪資基本維持不變的特性將其不予考慮，只在數學模型中包含航線補貼的計算，而略去基本工資總額。船舶i開往往返航班j支付給船員的總補貼為ρj·Cri，因此1天中往返航班總補貼P為

ρj·Cri(10)

式中：ρj為船舶往返航次數j的相關補貼系數；Cri為船舶i所有船員的基本航線補貼。

綜上所述，船隊1天的成本最小化目標函數為

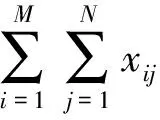
2.2.2 空載率最小化

班輪在營運過程中，在滿足當天游客數量的前提下，使船舶空載率最小化，充分利用船舶的運營空間，其中的客流量Fpk使用現有的載客能力估計。于是有

,k∈SK(12)

式中：SJKk為航線k往返航班的集合；si為船舶i的座位數；Fpk為航線k的日平均客流量，人；SK為航線集合。

2.2.3 船舶調度次數差異最小化

為使船舶調度便利，M艘船舶在N個往返航班被調度的期望次數為N/M，故其第3個目標函數為

,i=1,2,…,M(13)

2.3 基于最小偏差法統一目標函數

綜合上面的目標函數，得到班輪調度的多目標優化模型為

(14)

根據上述多目標優化模型和最小偏差法[7]，得到統一的目標函數為

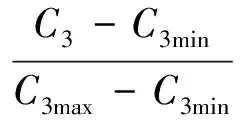
式中：C1max，C2max，C3max和C1min，C2min，C3min分別為各目標函數在約束條件作為單目標函數進行尋優求解的最大值和最小值。

2.4 約束條件

該船隊調度優化模型共有3組約束條件。

(1) 對于任一航班都須并且只須1艘船。

,i=1,2,3,…,M；j=1,2,3,…,N(16)

(2) 避免船舶在往返過程中的時間沖突。比如往返航班1和7的時間段有交集，不可能使用同一艘船舶。

xij1+xij2≤1

?i=1,2,…,M,j1,j2=1,2,3,…,N

且j1≠j2,Ωj1∩Ωj2≠?(17)

(3) 每艘船舶至少被調動1次，以充分利用船隊資源。

≥1,i=1,2,3,…,M(18)

3 算法運行和結果分析

3.1 基于最小偏差法遺傳算法尋優步驟

本文借助MATLAB中的GA Toolbox進行求解[9]。由于班輪調度屬于0-1整數規劃問題，這里采用工具箱中的整數規劃遺傳算法工具箱進行求解。

(1) 由于最小偏差法中須得到同等約束條件下多目標中各目標函數的最大值和最小值，傳統優化算法對初始解的選取較為敏感，為確保尋優結果，先采用MATLAB中遺傳算法工具箱進行單目標問題的模型構建和求解，得到其最大值和最小值。

(2) 利用式(1)中計算出的最大、最小值代入最小偏差法構建的多目標優化模型中，通過MATLAB工具箱進行求解。

3.2 優化結果及分析

在完成MATLAB平臺上優化模型的目標函數和約束條件的編寫后，運行該優化算法，在遺傳算法中，可以對其遺傳策略進行設置，不同的遺傳策略得到的優化方案不同。本文通過改變EliteCount這一遺傳參數來得到較優方案，然后將較優方案與原方案進行對比。班輪公司現采用的方案如表1所示。

表1 原調度方案

通過遺傳算法進行優化后的結果如表2所示，其過程如圖1所示，優化調度方案如表3所示。

表2 優化結果

圖1 遺傳算法優化過程

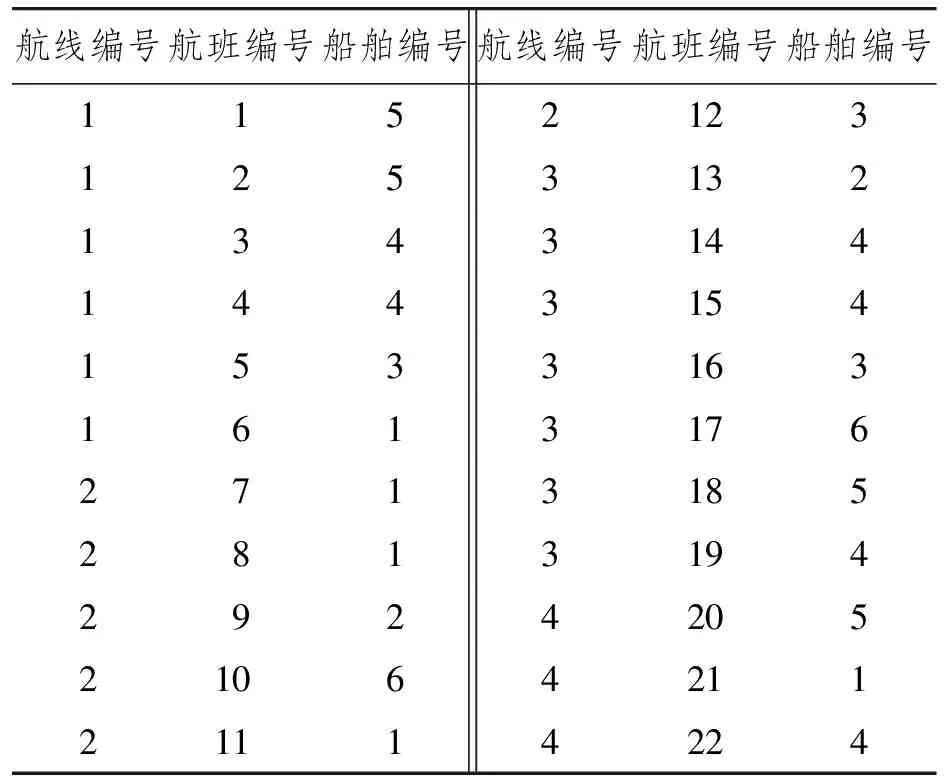
航線編號航班編號船舶編號航線編號航班編號船舶編號1152123125313213431441443154153316316131762713185281319429242052106421121114224

方案對比結果如表4所示。

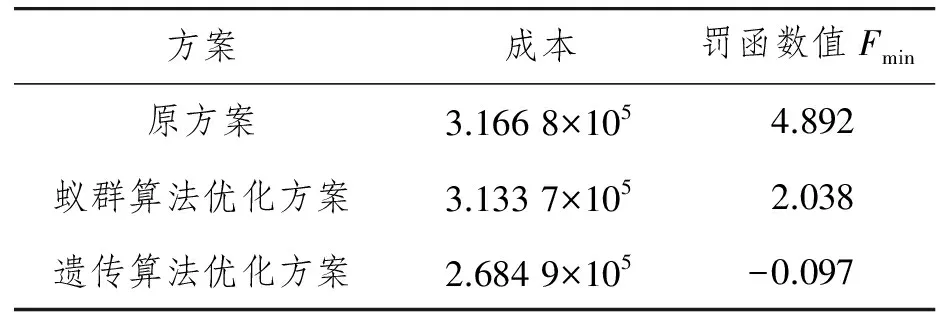
表4 3種方案的對比結果

由表4的數據分析可得：通過遺傳算法進行整數規劃得到的方案較原方案有明顯的優勢，除此之外，也比傳統蟻群算法優化得到的方案[10]較優。

4 結 論

本文利用實際船舶公司的數據對船舶調度問題進行分析研究，以MATLAB為計算平臺，構建遺傳算法優化模型，采用最小偏差法處理船舶調度中的多目標優化，得出以下結論：

(1) 文中針對的班輪調度優化結果與原方案進行對比可得：類似船舶調度類的問題可通過采用類似整數規劃的方式進行優化，這不僅可以將船舶運輸效率最大化，同時營運成本最小化。

(2) 本文采用的遺傳算法優化后結果與原方案相比較好，驗證了遺傳算法在多目標混合整數0-1規劃問題中的應用優勢性和合理性。

(3) 本文主要以MATLAB進行計算，可見MATLAB在工程計算中應用的便利性、合理性。

(4) 在船舶實際調度過程中還有很多因素參與影響，本文僅從成本、空載率和差異化這3個目標進行優化，故還須在日后的研究中考慮更多因素，完善調度方案，以使方案更貼近實際調度情況。

[ 1 ] 呂如福. 多目標船舶調度優化問題蟻群算法研究[D]. 杭州：浙江大學,2010.

[ 2 ] 王中華. 基于遺傳算法的港口船舶調度優化問題研究[D]. 上海：上海海事大學,2007.

[ 3 ] 王沖, 茅云生, 辛鍾桂. 基于遺傳算法的船舶分段運輸調度方法[J]. 上海交通大學學報, 2017, 51(3):338-343.

[ 4 ] 錢燕, 周良. 基于遺傳算法的不定期船舶調度優化模型研究[J]. 計算機與數字工程, 2014, 42(4):601-605.

[ 5 ] 周美英, 李典慶. 多目標優化設計的最小偏差法[J]. 機械設計, 2002, 19(12):50-52.

[ 6 ] LI W L, TAN J H. Optimization of Container Ship Principal Parameters based on Minimum-Deviation Method[J]. Shipbuilding of China, 2002, 43(4):1-5.

[ 7 ] WEI F T, SONG L, YAN L. Application of Minimum-Deviation Method to Mechanical Multi-Objective Optimal Design[J].Journal of Engineering Graphics, 2011, 32(3):100-104.

[ 8 ] 王文全, 黃勝, 侯遠航,等. 基于改進人工蜂群算法的大型艦船主尺度優化[J]. 武漢理工大學學報, 2012, 34(6):58-62.

[ 9 ] 周俊杰.Matlab/Simulink實例講解[M]. 北京：中國水利水電出版社,2014.

[10] 張新宇, 林俊, 郭子堅,等. 基于模擬退火多種群遺傳算法的港口船舶調度優化[J]. 中國航海, 2016, 39(1):26-30.