某異形彈丸的氣動特性研究

黃銀柳,陶如意,王 驍,陳燕婷

(南京理工大學 能源與動力工程學院， 南京 210094)

對于各種炮彈、航彈、火箭彈和導彈， 若配制子母戰斗部，將能構成大縱深突擊和大面積壓制火力，能夠有效地阻擊敵人的坦克、裝甲車等重要軍事目標[1]。2009年至今，伴隨著科技的不斷進步發展，計算機技術的不斷提高，數值模擬技術越來越受到廣大科研工作者的青睞[2-6]。在CFD軟件出現之前，常采用風洞實驗計算空氣動力，其邊界效應、支架干擾無法滿足相似準則等缺點無法避免。Fluent軟件的應用和發展，使空氣動力的計算變得越發便捷與準確，克服了風洞實驗的不足之處。Fluent模擬從不可壓縮到高度可壓縮范圍內的復雜流動，由于采用多重網格加速收斂技術和求解，可得到最佳的求解精度和收斂速度[7]。

但是，在相關的飛行物氣動特性計算中，其所涉及的結構多為常見的圓柱狀，當彈體飛行時，整個彈體的受力較為均勻。本文所述則是較為少見的縱截面為近梯形的子彈彈體。后部為4片長方形翼型尾翼。子彈從母彈殼體分離后，尾翼會展開到預設的角度，子彈彈體及尾翼兩端呈軸對稱。彈體形狀的變化對氣動特性產生很大的影響，升力、阻力、俯仰力矩等都會隨之改變。本文針對某異形彈丸飛行時的氣動特性問題，利用FLUENT軟件對縱截面為近梯形的彈丸進行定常數值仿真計算，通過建立異形彈體的幾何模型、網格劃分、FLUENT中的相關參數進行設置并迭代計算，得到彈丸在不同攻角和馬赫數下的升力系數、阻力系數、俯仰力矩系數，為進一步研究異形彈體的氣動特性和彈道特性提供了理論依據。

1 彈丸的物理模型與網格劃分

用ANSYS軟件包中的前置處理器ICEM，按照由點到線，由線到面，由面到體的原則對彈體進行建模。幾何模型縱剖面為近梯形，尾翼采用四翼式布局，翼型為長方形。彈體特征長度1 000 mm，最大直徑115 mm，最小直徑35 mm。為減小風阻，頭部小圓柱體結合處采用倒角。彈體左右對稱，采用一半進行計算。計算模型如圖1所示。根據尺寸比例在彈體外圍設置一個繞流流場：外圍計算域采用長度為8倍彈長、寬度為5倍彈長，高度為3倍彈長的立體域。設置6層彈體棱柱邊界層，并在機翼附近加密。網格劃分如圖2所示。

2 計算模型

Fluent軟件包含豐富的物理模型，例如相變模型、輻射模型、離散相變模型、多相流模型、化學組分輸運和反應流模型、計算流體流動和熱傳導模型(其中包括層流、湍流、定常與非定常流動、自然對流、不可壓縮與可壓縮流動、周期流、旋轉流、時間相關流動等)。針對需要解決的物理問題流動特點，軟件中都有較為適合的數值解法。選擇顯式或隱式差分格式，可以在整體穩定性、計算精度與速度等方面達到最佳效果。

可用的湍流模型各有其優點與缺點。雷諾應力模型可以較好的處理各向異性較強的湍流流動，但不適合于一般的回流流動，且其計算量巨大，結構復雜。方程如下[8-9]：

Dij+φij+Gij-εij

(1)

其中：Dij為擴散項；φij為壓力應變項；Gij為產生項；εij為耗散項。

大渦模擬適用于各種高雷諾數流動，其對網格的質量要求極為嚴格。N-S方程為

(2)

修正N-S方程為

(3)

其中

(4)

k-ε湍流模型則是最廣泛應用的一種湍流模型，能夠比較精確地預測平面和圓形射流的散步率。其中，湍流動能方程為

Gk+Gb-ρε-YM+SK

(5)

擴散方程為

(6)

湍流模型采用單方程Spalart-Allmaras模型。其優點是只需要求解湍流黏性運輸方程，剪切層厚度則不用計算，魯棒性好，不需要精確的網格劃分且計算量不大，較適用于此類空氣流動問題。其方程為

(7)

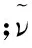
3 計算求解

1) 以ICEM對彈丸的相關區域劃分網格并優化，檢查網格質量，無誤后輸出網格文件。

2) 將網格文件導入FLUENT中，檢查最小網格尺寸是否大于0。使用基于密度耦合求解器，選擇上述單方程湍流模型。

3) 選擇氣體黏度滿足薩蘭德定理的物理屬性設置，以理想氣體做介質。

4) 壁面邊界條件：無滑移。

5) 差分格式選擇：動量、湍流動能以及湍流耗散率均選用二階迎風格式；壓力差值設為默認。

6) 邊界條件設置大氣壓為101 325 Pa，馬赫數與攻角數見下文所述。

7) 設置松弛因子：壓力項設為0.7，密度與質量設為1，動量項設為0.6，湍動能項、湍流黏性項與耗散率項均設為0.5。

8) 定義對稱面為SYMMERY，其余計算域邊界條件設為PRESSURE-FAR-FIELD。

9) 定義監視器，進行6 000步的迭代計算[10-13]。

4 氣動特性計算結果與分析

初始階段，在給定的攻角和來流馬赫數下，升力系數、阻力系數和俯仰力矩系數隨著迭代次數的不斷增加而產生震蕩。一直到迭代次數超過2 500步后，波動明顯減弱，曲線趨于平穩，就可以在圖中讀出升力系數、阻力系數、俯仰力矩系數等相關參數的數值。圖3是升力系數隨迭代過程變化曲線，圖4是阻力系數隨迭代過程變化曲線，圖5是俯仰力矩系數隨迭代過程變化曲線。可以看出，彈體氣動特性收斂，表明系統的設計較為穩定。從圖6可得，彈頭和翼梢前端所受壓強最大。

4.1 升力特性分析

在0°、3°、6°、9°、12°攻角下，進行不同馬赫數下的仿真實驗，得到升力系數變化曲線(圖7)如下：

從圖7可以看出，在相同的攻角條件下，由于來流馬赫數不同，升力系數由大到小的順序為0.6Ma、0.5Ma、0.4Ma，即彈丸的升力系數隨著來流馬赫數的增加而增大。對于攻角來說，在來流馬赫數相同的情況下，升力系數隨著攻角的增加而增大。攻角在0°～ 6°時，升力系數與攻角成準線性關系；在6°～9°時，升力系數極速上升；超過9°后，升力系數曲線又回歸平緩，升力系數隨攻角增加而增大的趨勢減小。

4.2 阻力特性分析

在0°、3°、6°、9°、12°攻角下，進行不同馬赫數的仿真實驗，得到阻力系數變化曲線如圖8。

從圖8可以看出，在相同的攻角條件下，由于來流馬赫數不同，阻力系數由大到小的順序為0.6Ma、0.5Ma、0.4Ma，即彈丸的阻力系數隨著來流馬赫數的增加而增大，且系數增加的幅度大致相同。對于攻角來說，在來流馬赫數相同的情況下，阻力系數隨著攻角的增加而增大，攻角在0°～ 12°時，阻力系數與攻角成準線性關系，只是在攻角超過9°時，阻力系數隨攻角增加而增大的趨勢稍微增大。

4.3 俯仰力矩特性分析

在0°、3°、6°、9°、12°攻角下，進行不同馬赫數下的仿真實驗，得到俯仰力矩系數變化曲線如圖9。

從圖9可以看出，俯仰力矩系數與升力系數和阻力系數曲線不同，并沒有呈現直上或直下的趨勢。攻角為0°～3°時，隨著攻角的增加，俯仰力矩系數緩慢減小；攻角為3°～9°時，隨著攻角的增加，俯仰力矩系數成準線性關系快速減小；攻角超過9°后，俯仰力矩系數又呈現出快速上升的趨勢。

5 結論

本文利用Fluent軟件通過數值模擬了不同來流馬赫數和不同攻角下某異形彈丸的氣動流場，并發現了該異形彈丸氣動參數的基本變化規律。研究結果為非常規彈丸彈道特性的深入研究提供了參考和依據。

參考文獻：

[1] 祁少文.子母彈拋撒子彈過載測試技術研究[D].太原：中北大學,2015.

[2] 李嗄.氣囊式子母彈拋撒過程數值模擬[D].南京：南京理工大學,2012.

[3] 張博孜.子母彈中心燃氣式拋撒內彈道過程研究[D].南京：南京理工大學,2015.

[4] 張博孜,王浩.含擾流裝置的中心燃氣式拋撒內彈道過程的數值模擬[J].爆炸與沖擊,2015,35(2):208-214.

[5] 王帥.子母彈囊式拋撒系統實驗研究及數值仿真[D].南京：南京理工大學,2013.

[6] 陶如意.子母戰斗部系統仿真平臺設計與實現[J].系統仿真學報,2010,22(5):1121-1124.

[7] 李楠,倪原,李聚峰,等.基于Fluent的飛行器氣動參數計算方法[J].現代電子技術,2014,423(16):68-70.

[8] 王堃,買瑞敏.基于CFD軟件的制導兵器氣動特性[J].兵工自動化,2011,30(5):89-90.

[9] 伍星,盧永剛,宋瓊,等.基于Fluent的彈體氣動特性計算與分析[J].兵器裝備工程學報,2016,37(2):22-25.

[10] 郭江濤,邢存震,譚獻忠.基于Fluent的亞音速翼型氣動特性數值研究[J].中原工學院學報,2012,23(1):36-40.

[11] 李盛宏.使用FLUENT對某飛行器的氣動特性模擬[D].北京：北京大學,2003.

[12] 吳志林,陶家賓.基于FLUENT的微型修正彈藥氣動特性仿真[J].計算機仿真,2013,30(6):20-23.

[13] 胡志鵬,劉榮忠,郭銳.基于FLUENT的雙翼末敏彈氣動特性研究[J].飛行力學,2013(1):53-56.

[14] 管軍，周家勝，易文俊，等. 基于自適應混沌變異粒子群優化算法的旋轉彈丸氣動參數辨識[J].兵工學報，2017(1):73-80.