城市軌道交通乘客半補償路徑選擇建模與應用

張永生，姚恩建，劉莎莎，蔡昌俊，2

(1.北京交通大學 交通運輸學院，北京 100044； 2.廣州地鐵集團有限公司，廣東 廣州 510310)

在城市軌道交通網(wǎng)絡中，換乘站銜接了不同的線路，使得乘客的備選路徑往往不止一條。城軌乘客路徑選擇模型通過綜合考量多種因素以確定各路徑的選擇比例，進而估算換乘量、斷面流量、線路流量等，為線路規(guī)劃、客流組織、運行計劃編制、票務清分等業(yè)務提供數(shù)據(jù)支撐。尤其當新線接入等導致路網(wǎng)結構發(fā)生變化時，基于刷卡數(shù)據(jù)的清分模型[1-3]等數(shù)據(jù)驅動方法難以應用，而基于離散選擇理論的路徑選擇模型是從乘客的行為解釋角度出發(fā)，揭示不同因素對乘客的影響程度，因此，該模型可以應用到網(wǎng)絡結構發(fā)生變化后的場景中。

目前，基于離散選擇理論的路徑選擇模型主要以Multinomial Logit(MNL)模型[4]及其衍生模型為主。在軌道交通路徑選擇行為分析方面，文獻[5-10]分別從模型的應用推廣、模型的理論演化和不同數(shù)據(jù)源下模型推導等不同角度進行了嘗試，充分證明了該類模型的優(yōu)越性。文獻[11-15]逐漸增加了地鐵服務水平、個體屬性、出行目的、路網(wǎng)拓撲結構等因素對城軌乘客路徑選擇偏好的影響分析，從行為學角度完善了模型的可解釋性。

基于離散選擇理論的路徑選擇模型利用微觀經(jīng)濟學和行為學詮釋了出行者實際的決策過程。通過綜合權衡各因素的優(yōu)劣，出行者從有效路徑集合中挑選出感知效用最大的路徑。這是一個半補償?shù)倪^程，即有效路徑集合生成(非補償)與路徑擇優(yōu)(補償)的結合[16]。非補償表示有效的路徑不能超過某因素(如：時間)的容忍閾值；補償表示考慮各因素的綜合效果，從所有有效的路徑中選出最優(yōu)的路徑。但既有研究中，有效路徑集合的判斷閾值大都根據(jù)主觀經(jīng)驗或其他調查數(shù)據(jù)外生標定，導致閾值與乘客的選擇行為脫節(jié)。即在當前城市軌道交通的乘客路徑選擇建模方面，學者們大都只關注補償性的各影響因素間相互替代關系的求解和應用，而忽視了非補償性的有效路徑集合閾值的合理估算及它們之間的內在關聯(lián)性。

本文構建城軌乘客半補償Mixed Logit(ML)路徑選擇模型，一方面內生性地求解各影響因素的系數(shù)和有效路徑集合閾值，解析城軌乘客路徑選擇的半補償過程，另一方面以ML模型結構[17]防止MNL模型選擇肢間獨立不相關的假設的影響，準確反映不同乘客間的差異性(異質性)，包括補償性選擇過程的差異性和非補償性有效路徑集合構造過程中乘客容忍閾值的差異性。考慮到所建模型結構的相對復雜性，將馬爾科夫鏈蒙特卡洛法與數(shù)據(jù)擴張技術進行融合，搭建出參數(shù)估算方法。以在廣州地鐵得到的調查數(shù)據(jù)，對所建模型進行標定，并對其在新線接入條件下的預測性能進行分析。

1 城軌乘客半補償ML路徑選擇模型

1.1 城軌乘客路徑選擇的半補償性與異質性體現(xiàn)

圖1是基于2013年7月在廣州地鐵進行問卷調查得到的統(tǒng)計結果(共14 142個樣本)。圖1(a)描述的是若最短出行時間為30 min，乘客可容忍的最長出行時間(預設6個選項供被調查者選擇1項)；圖1(b)統(tǒng)計的是最少換乘次數(shù)為0次時，乘客對容忍閾值選擇的結果。上述結果說明乘客對路徑的出行時間和換乘次數(shù)都有一定的容忍限制，即有效路徑集合是滿足一定限制條件的路徑的集合。同時，不同閾值形成不同的有效路徑集合將導致不同的模型估計結果，即閾值參數(shù)與效用函數(shù)系數(shù)有內在關聯(lián)性，外生估計的閾值將導致有偏的效用函數(shù)系數(shù)，不能準確反映城軌乘客的路徑選擇行為。上述現(xiàn)象體現(xiàn)了半補償性對城軌乘客路徑行為的影響。而且，圖1還顯示出乘客在閾值上的差異性。因此，本文將閾值設置為隨機變量，以體現(xiàn)乘客對閾值的異質性，并聯(lián)立非補償性的有效路徑集合構造和補償性的路徑選擇兩個過程，內生地估計效用函數(shù)和閾值的各參數(shù)。

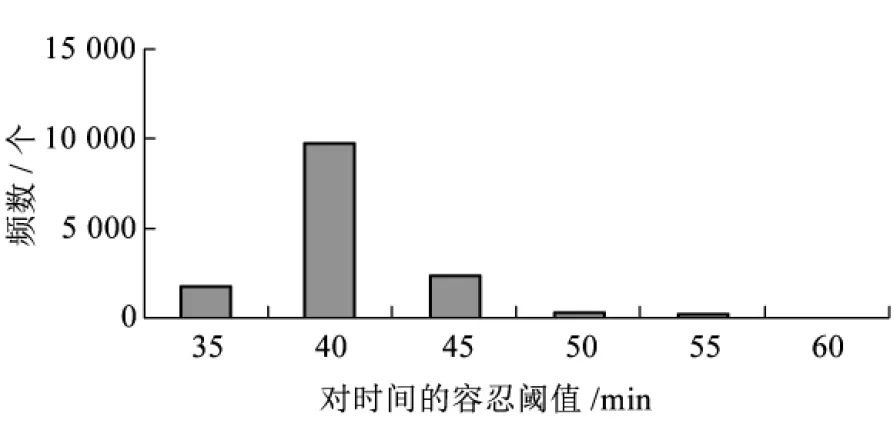
(a)時間容忍閾值分布(相對于30 min)

(b)換乘次數(shù)的容忍閾值分布(相對于0次)圖1 容忍閾值例證

1.2 城軌乘客半補償路徑選擇模型

考慮到有效路徑集合生成過程和路徑選擇過程的先后順序，基于貝葉斯理論，以有效路徑集合的選擇為先驗知識，構造半補償選擇模型。

( 1 )

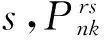
1.3 非補償性選擇部分

( 2 )

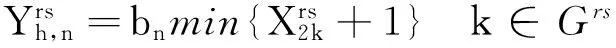
( 3 )

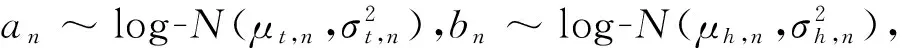
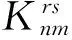
( 4 )

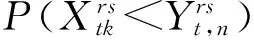
( 5 )

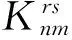
( 6 )

在成網(wǎng)條件下，城市軌道交通中同一OD對間的路徑條數(shù)是很多的，通過任意組合，有效路徑集合的數(shù)量更是龐大，為節(jié)省計算時間，同時考慮到大多數(shù)路徑被考慮的概率基本為0，因此路徑總集合Grs一般設置為有可能被選擇到的路徑的集合。考慮到目前城市軌道交通路網(wǎng)的規(guī)模，本文分別以最短出行時間和最少換乘次數(shù)為標準各取前3條路徑，即同一OD對間的路徑總集合Grs最多有6條不同路徑，有效路徑集合的個數(shù)最多為63個。

1.4 補償性選擇部分

基于隨機效用理論，對于出行者n而言，從起點r到終點s的第k條路徑的隨機效用為

( 7 )

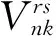
為體現(xiàn)乘客在補償性選擇過程中的差異性，同時避免MNL模型選擇肢獨立不相關假設的影響，本文構造了Mixed Logit路徑選擇模型，該模型假設特征變量參數(shù)為隨機變量。

( 8 )

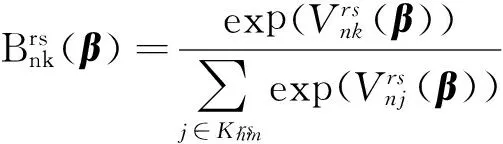
( 9 )

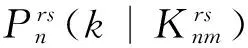
換乘次數(shù)與乘車時間的量綱不同，為對比兩者對乘客路徑選擇偏好的影響，利用“等效乘車時間系數(shù)”[14]將換乘次數(shù)轉化為等車時間。

2 半補償ML路徑選擇模型求解算法

2.1 參數(shù)選擇

各參數(shù)的隨機分布形式一般包括均勻分布、對數(shù)正態(tài)分布、正態(tài)分布、SB分布和三角分布等[17]。考慮到參數(shù)符號的意義和參數(shù)估算難度，本文將分別基于對數(shù)正態(tài)分布、正態(tài)分布和固定值等三種形式進行參數(shù)估算，選擇出最優(yōu)結果。

2.2 參數(shù)估計

鑒于參數(shù)估計時積分運算的復雜性，本文通過融合馬爾科夫鏈蒙特卡洛法與數(shù)據(jù)擴張技術[18]，估算參數(shù)，步驟如下：

設未知參數(shù)為θ=(μY，σY，μβ，σβ)，其中(μY，σY)為閾值參數(shù)的分布參數(shù)；(μβ，σβ)為特征變量參數(shù)β的分布參數(shù)。

步驟1隨機產(chǎn)生參數(shù)θl。當l=0時，θl=0；當l≥1時，基于θl～N(θl-1，σ)(其中σ根據(jù)參數(shù)范圍設定為常數(shù))獲得隨機參數(shù)θl，并基于θl中的特征變量參數(shù)的分布參數(shù)獲得一組隨機值βl。

步驟3計算似然函數(shù)。改造的似然函數(shù)為

P(βl|(μβ l，σβ l))

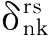
步驟4令λ=ln(Ll)-ln(Ll-1)，并進行如下判斷：當λ≥0時，θl=θl；當λ<0時，產(chǎn)生服從U(0，1)的隨機數(shù)τ，當λ≥ln(τ)，θl=θl，否則θl=θl-1，Ll=Ll-1。

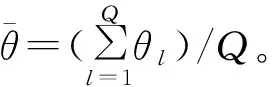
上述參數(shù)估算方法主要依托于SP(StatedPreference)或RP(RevealedPreference)調查數(shù)據(jù)。通過調查獲得乘客對路徑的選擇結果，以此估算乘客路徑選擇時的行為偏好參數(shù)。本文所建模型從行為解釋角度挖掘了各種因素對乘客路徑選擇的影響程度，該影響程度在短期內(如3～5年)一般不會發(fā)生明顯變化，也不會隨著路網(wǎng)的擴張而變，因此所標定的參數(shù)在短期內應用時，無需重新標定或調整，適用于日益復雜的軌道交通運營環(huán)境。

3 實例分析

3.1 數(shù)據(jù)基礎

2013年年底廣州地鐵開通六號線，該線路自西向東，穿過市區(qū)，與既有線路形成了7個換乘站，路網(wǎng)結構發(fā)生較大變化。本文基于六號線開通之前的調查數(shù)據(jù)標定模型，分析模型的統(tǒng)計效果，預測六號線開通后的路徑選擇比例，檢驗所建模型在應用時的預測性能。所用調查數(shù)據(jù)來源于2013年7月針對廣州地鐵乘客出行特征的調查，主要包括個體屬性、乘客此次出行實際選擇的路徑、乘客對時間和換乘次數(shù)的容忍閾值等信息，有效樣本量為14 142份。

3.2 模型標定結果

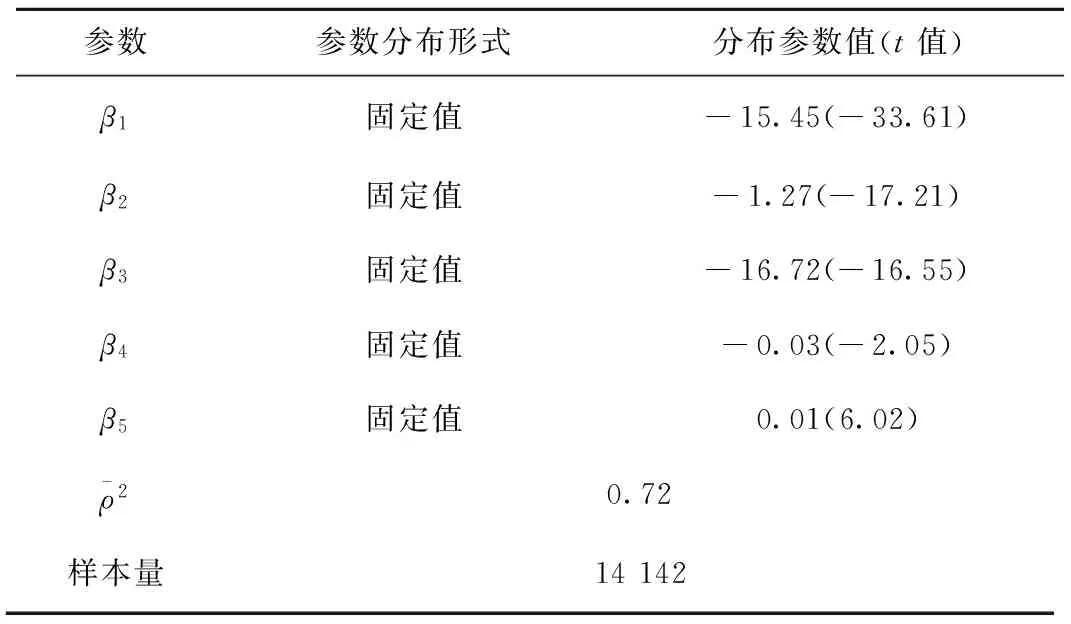
表1 MNL路徑選擇模型參數(shù)標定結果

表2 ML路徑選擇模型參數(shù)標定結果

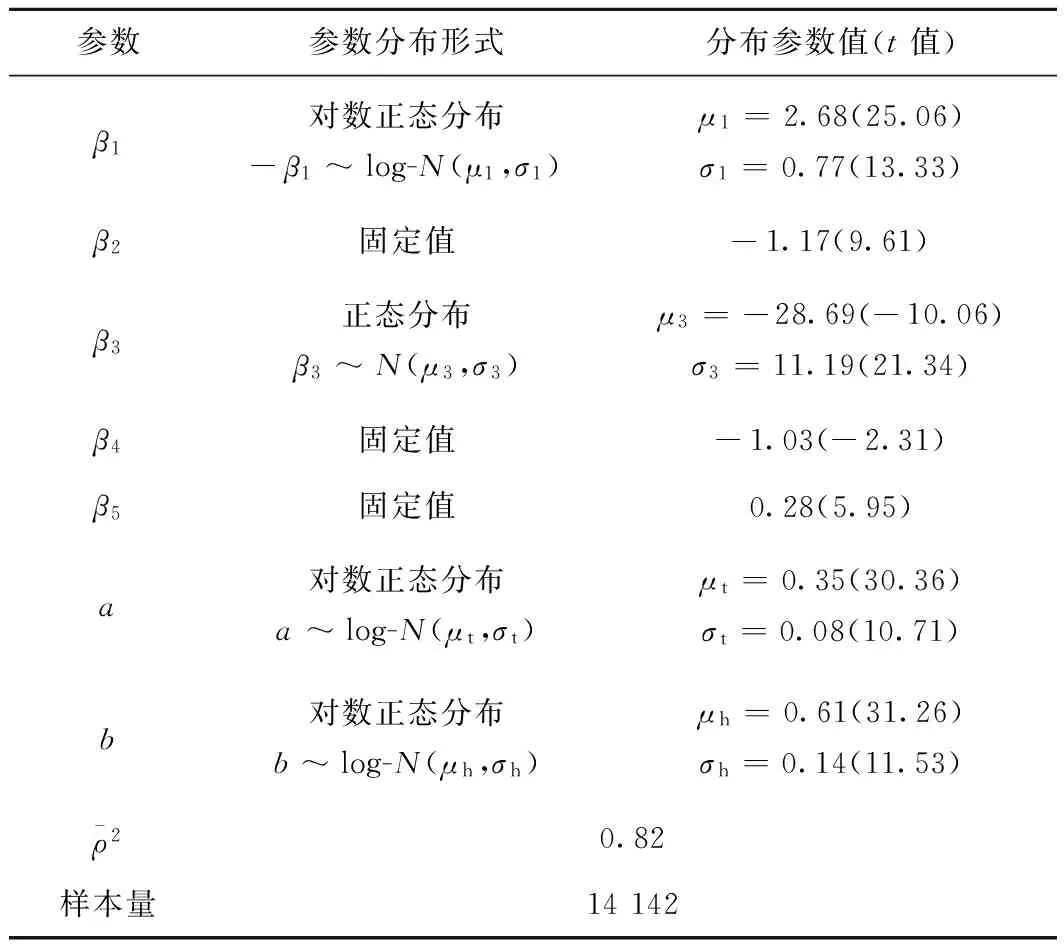
表3 半補償ML路徑選擇模型參數(shù)標定結果

分析以上3個表中的數(shù)據(jù)，可得到以下結論：

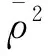
(2)乘車時間、換乘次數(shù)、換乘時間以及角度費用的系數(shù)取值為負數(shù)，表示乘客更傾向于選擇時間短、費用低、換乘次數(shù)少的路徑。舒適程度的系數(shù)為正值，表示乘客傾向于選擇更舒適的路徑。

(3)在表2和表3中，換乘時間的系數(shù)服從于正態(tài)分布，雖然會出現(xiàn)換乘時間的系數(shù)為正的缺點，但其所占比例分別僅為Φ(-29.4/10.89)=0.35%，Φ(-28.69/11.19)=0.52%，可以忽略不計。

進一步觀察，表3中的出行時間和換乘次數(shù)閾值參數(shù)均服從于對數(shù)正態(tài)分布。其中，出行時間閾值參數(shù)a的數(shù)學期望為1.42，方差為0.01，即平均來講，超過最短出行時間1.42倍的路徑，不會被乘客考慮；換乘次數(shù)閾值參數(shù)b的數(shù)學期望為1.86，方差為0.07，即平均來講，令最少換乘次數(shù)加1次，超過該值1.86倍的路徑，不會被乘客考慮。對比圖1的調查結果，乘客對30 min的容忍閾值的均值為40.5 min，而標定結果1.42×30=42.6 min；乘客對換乘0次的容忍閾值的均值為1.95次，而標定結果為1.86×(0+1)=1.86次。結果說明標定結果符合實際，更精準(調查結果為離散值，其均值并不精準)。

而且，為對比乘車時間和換乘次數(shù)對城軌乘客路徑選擇偏好的影響，可進行等效乘車時間分析。由于-β1～log-N(μ1，σ1)，則ln(-β1)～N(μ1，σ1)，進而ln(β2/β1)=[ln(-β2)-ln(-β1)]，因此可得到ln(β2/β1)～N(ln(-β2)-μ1，σ1)，即β2/β1為對數(shù)正態(tài)分布，β2/β1～log-N(ln(-β2)-μ1，σ1)。換乘次數(shù)的等效乘車時間系數(shù)的單位為h/次，該值較小，為便于描述，將等效乘車時間系數(shù)的單位調為min/次，即60·β2/β1～log-N(ln(-60·β2)-μ1，σ1)，如圖2所示，其數(shù)學期望值為6.6 min/次，即換乘1次相當于乘車時間6.6 min。

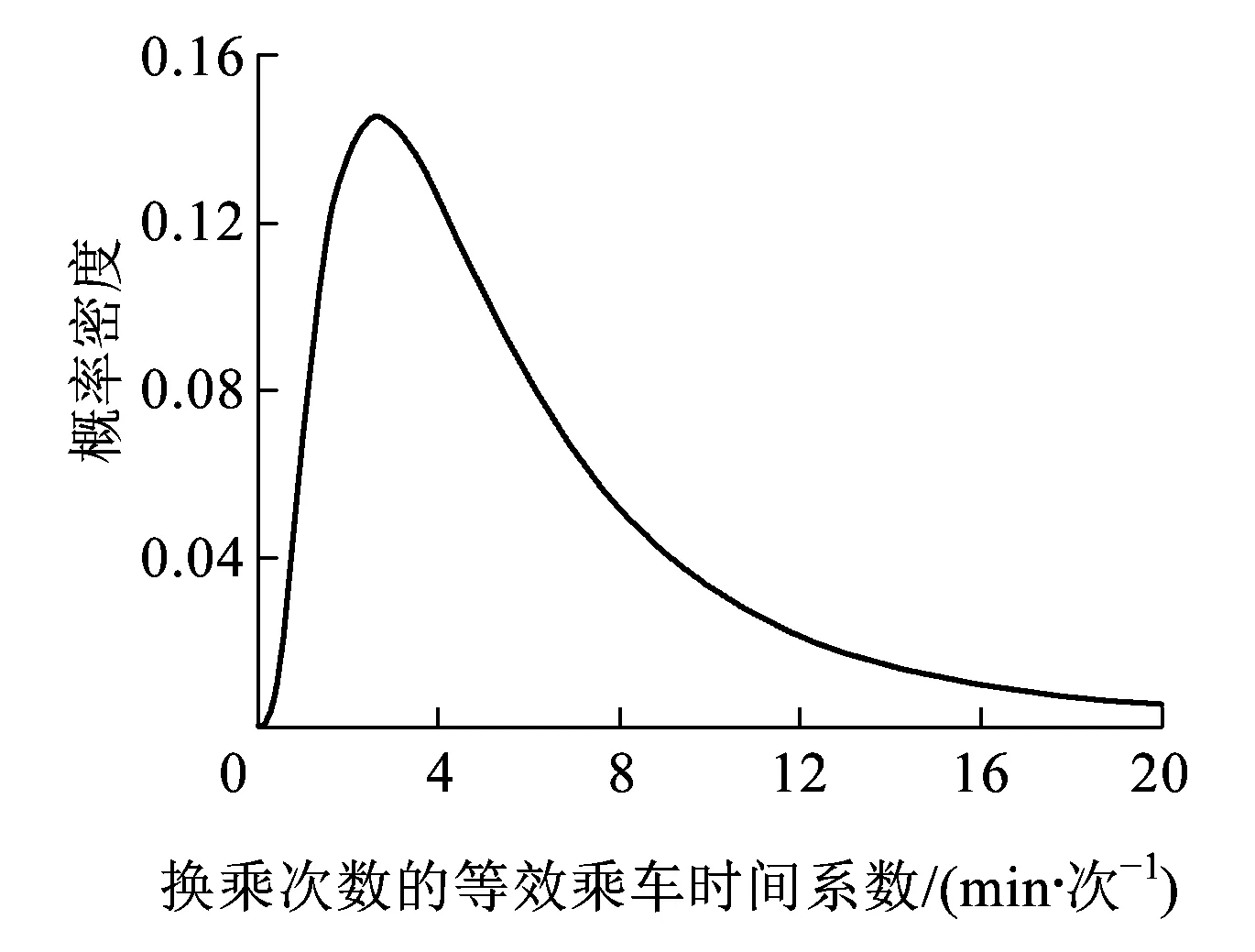
圖2 換乘次數(shù)的等效乘車時間系數(shù)對數(shù)正態(tài)分布概率密度圖

3.3 模型應用

換乘量預測值是進行換乘站設計和換乘客流組織預案編制的基礎。本文通過路徑選擇模型預測換乘量，一方面可體現(xiàn)路徑選擇模型的應用價值，另一方面可用來校驗所建模型的預測效果。在實際應用中，需首先確定路徑總集合和各影響因素的取值，進而基于標定的路徑選擇模型計算站點間各條路徑的選擇比例，結合站點間客流量，統(tǒng)計換乘量。模型應用時各變量的取值原則與模型標定時類似，其中，運營管理部門可提供預計的列車運行計劃、換乘走行時間和滿載率(新路段的滿載率初始值為0)。本文以上述六號線開通前的調查結果標定的模型為基礎，利用廣州地鐵集團有限公司提供的2014年3月(六號線開通后)的路網(wǎng)數(shù)據(jù)、列車運行計劃、滿載率與換乘走行時間，分別以最短出行時間和最少換乘次數(shù)為標準各取前3條路徑組成路徑總集合，并計算出各條路徑各變量的取值，進而基于式( 1 )判斷每個時間窗(此處以15 min為一個時間窗)下路徑總集合中各條路徑的選擇比例，乘以對應時間窗下站點間客流量，通過統(tǒng)計得到預測的六號線開通后的各換乘站各換乘流向(如：十字交叉式的換乘站共有8個換乘流向)全天換乘量(共19個換乘站，138個換乘流向)，詳見文獻[14]的描述，并以廣州地鐵集團有限公司提供的清分結果為校驗值。如圖3所示，縱軸為預測值，橫軸為校驗值，數(shù)據(jù)點圍繞在45°線附近，說明預測值接近于校驗值。經(jīng)計算，平均相對誤差為5.19%，滿足運營管理部門的業(yè)務需求。

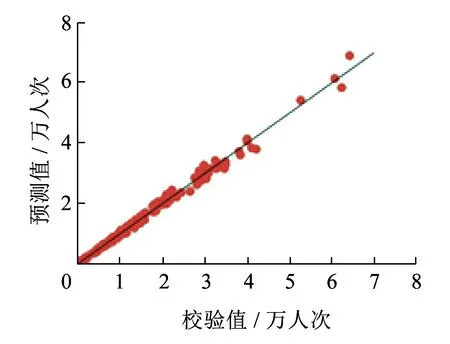
圖3 全天換乘量預測校驗45°線圖

4 結論

路徑選擇過程是有效路徑集合生成和路徑擇優(yōu)兩個過程的統(tǒng)一，同時乘客間的差異性不僅表現(xiàn)在選擇偏好的差異，還表現(xiàn)在有效路徑集合閾值的差異。本文針對既有研究對上述兩個過程的孤立和對乘客間異質性的考量不足等缺點，構建城軌乘客半補償ML路徑選擇模型，不僅將上述兩個過程統(tǒng)一為整體，實現(xiàn)了效用函數(shù)參數(shù)和閾值的內生標定，還充分考慮了乘客間的異質性。基于RP調查數(shù)據(jù)對模型進行標定，可以得到如下結論：

(1)所建半補償ML模型在擬合效果和預測效果上均優(yōu)于一般的MNL模型和ML模型。

(2)換乘時間的等效乘車時間系數(shù)為對數(shù)正態(tài)分布。經(jīng)計算，數(shù)學期望為6.6 min/次，表明平均來講，換乘1次相當于乘車6.6 min。

(3)出行時間和換乘次數(shù)閾值均服從于對數(shù)正態(tài)分布，根據(jù)其期望值對比實際調查結果，證實了標定結果的合理性。

本文探討了所建模型的應用效果，針對廣州地鐵六號線接入導致路網(wǎng)結構發(fā)生巨大變化的場景，預測了各換乘站換乘量，對比校驗值，平均相對誤差為5.19%，證明所建模型可以較好地適應網(wǎng)絡結構變化條件下的客流預測。

參考文獻：

[1]SUN Y,XU R.Rail Transit Travel Time Reliability and Estimation of Passenger Route Choice Behavior[J].Transportation Research Record,2012,2275(1):58-67.

[2]ZHOU F,SHI J,XU R.Estimation Method of Path-selecting Proportion for Urban Rail Transit Based on AFC Data[J].Mathematical Problems in Engineering,2015,2015(6):1-9.

[3]SUN L,JIN J,LEE D H,et al.Characterizing Travel Time Reliability and Passenger Path Choice in a Metro Network[C]//Proceedings of Transportation Research Board-94th Annual Meeting.Washington D C:TRB Publisher,2015:1-16.

[4]MCFADDEN D.The Revealed Preferences of Government Bureaucracy[J].The Bell Journal of Economics,1975,6(2):401-416.

[5]YAO E,MORIKAWA T.A Study on Integrated Intercity Travel Demand Model[J].Transportation Research Part A:Policy and Practice,2005,39(4):367-381.

[6]DAAMEN W,BOVV P H L,HOOGENDOOM S P,et al.Passenger Route Choice Concerning Level Changes in Railway Stations[C]//Proceedings of Transportation Research Board-84th Annual Meeting.Washington D C:TRB Publisher,2005:1-18.

[7]四兵鋒,毛保華,劉智麗.無縫換乘條件下城市軌道交通網(wǎng)絡客流分配模型及算法[J].鐵道學報,2007,29(6):12-18.

SI Bingfeng,MAO Baohua,LIU Zhili.Passenger Flow Assignment Model for Urban Railway Traffic Network under the Condition of Seamless Exchange[J].Journal of the China Railway Society,2007,29(6):12-18.

[8]徐瑞華,羅欽,高鵬.基于多路徑的城市軌道交通網(wǎng)絡客流分布模型及算法研究[J].2009,31(2):110-114.

XU Ruihua,LUO Qin,GAO Peng.Passenger Flow Distribution Model and Algorithm for Urban Rail Transit Network Based on Multi-route Choice[J].Journal of the China Railway Society,2009,31(2):110-114.

[9]劉劍鋒,孫福亮,柏赟,等.城市軌道交通乘客路徑選擇模型及算法[J].交通運輸系統(tǒng)工程與信息,2009,9(2):85-90.

LIU Jianfeng,SUN Fuliang,BAI Yun,et al.Passenger Flow Route Assignment Model and Algorithm for Urban Rail Transit Network[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(2):85-90.

[10]SUN L,LU Y,JIN J,et al.An Integrated Bayesian Approach for Passenger Flow Assignment in Metro Networks[J].Transportation Research Part C:Emerging Technologies,2015,52(1):116-131.

[11]RAMMING M S.Network Knowledge and Route Choice[D].Massachusetts:Massachusetts Institute of Technology,2001:111-212.

[12]SEBASTIAN R,MUNOZ J C,GRANGE L D.A Topological Route Choice Model for Metro[J].Transportation Research Part A:Policy and Practice,2011,45(2):138-147.

[13]SEBASTIAN R,ZHAN G,JUAN C M,et al.A Behavioral Comparison of Route Choice on Metro Networks:Time,Transfers,Crowding,Topology and Socio-demographics[J].Transportation Research Part A:Policy and Practice,2014,66(1):185-195.

[14]張永生,姚恩建,代洪娜.成網(wǎng)條件下地鐵換乘量預測方法研究[J].鐵道學報,2013,35(11):1-6.

ZHANG Yongsheng,YAO Enjian,DAI Hongna.Transfer Volume Forecasting Method for the Metro in Networking Conditions[J].Journal of the China Railway Society,2013,35(11):1-6.

[15]劉莎莎,姚恩建,張永生.軌道交通乘客個性化出行路徑規(guī)劃算法[J].交通運輸系統(tǒng)工程與信息,2014,14(5):100-104.

LIU Shasha,YAO Enjian,ZHANG Yongsheng.Personalized Route Planning Algorithm for Urban Rail Transit Passengers[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(5):100-104.

[16]BEN-AKIVA M E,BOCCARA B.Discrete Choice Models with Latent Choice Sets[J].International Journal of Research in Marketing,1995,12(1):9-24.

[17]MCFADDEN D,TRAIN K.Mixed MNL Models for Discrete Response[J].Journal of Applied Econometrics,2000,15(5):447-470.

[18]DAVID A D,MENG X.The Art of Data Augmentation[J].Journal of Computational and Graphical Statistics,2001,10(1):1-50.