新型二維輪軌耦合單元及OpenSees實現
古 泉,李維泉,國 巍,劉永斗,蔣麗忠,余志武
(1.廈門大學 建筑與土木工程學院,福建 廈門 361005;2.廈門大學 廈門市交通基礎設施智能管養工程技術研究中心,福建 廈門 361005;3.中南大學 土木工程學院,湖南 長沙 410075;4.中南大學 高速鐵路建造技術國家工程實驗室,湖南 長沙 410075)
業內學者[1-3]對車橋耦合問題進行了系統研究,其中二維(豎向)車橋耦合理論和數值方法可歸納為如下三類:(1)子系統迭代求解[4]。將車輛子系統、軌道-橋梁子系統單獨建模,通過幾何關系和相互作用力的平衡關系協調兩個子系統的耦合。(2)濃縮自由度直接求解[5-8]。將車輪的響應(位移、速度和加速度)用與之接觸的軌道梁單元的響應基于形函數插值表示,并代入車輛子系統方程得到輪軌作用力,再將該作用力代入軌道-橋梁子系統方程,得到縮減自由度后的系統耦合方程,進行逐步積分求解。(3)耦合系統整體求解。該方法通過構造車輛-軌道耦合單元[9]、車輛-軌道-橋梁耦合單元[10-11]、輪軌耦合單元[12-13]等不同的時變單元,按照“對號入座”法則組裝系統的耦合振動方程,進行逐步積分求解。
本文提出一種基于非線性接觸關系的新型二維輪軌耦合單元,建立豎向車橋耦合系統有限元模型并進行地震動力分析。該單元有如下優勢:(1)易于集成到現有的通用有限元框架,編程難度低;(2)車輛運行中有限元模型無需修改,建模難度小;(3)能夠模擬輪軌間非線性接觸,可考慮車輛跳軌和軌道不平順激勵的影響。
本文在有限元OpenSees[14]軟件平臺實現了此單元,該平臺擁有豐富的材料庫和單元庫,在地震響應分析中具備優勢,這使得用戶能夠考慮復雜的工程實際,建立更加精細的車輛模型和軌道-橋梁模型。
1 二維輪軌耦合單元模型
二維輪軌耦合單元所在位置如圖1(a)所示,該單元由一個輪節點w和列車行進過程中所有可能與之接觸的梁單元節點序列[a,…,i,j,…,q]組成。當車輪運動t時間后,通過幾何關系可計算輪軌接觸點O與起始節點a的距離為X(t)。
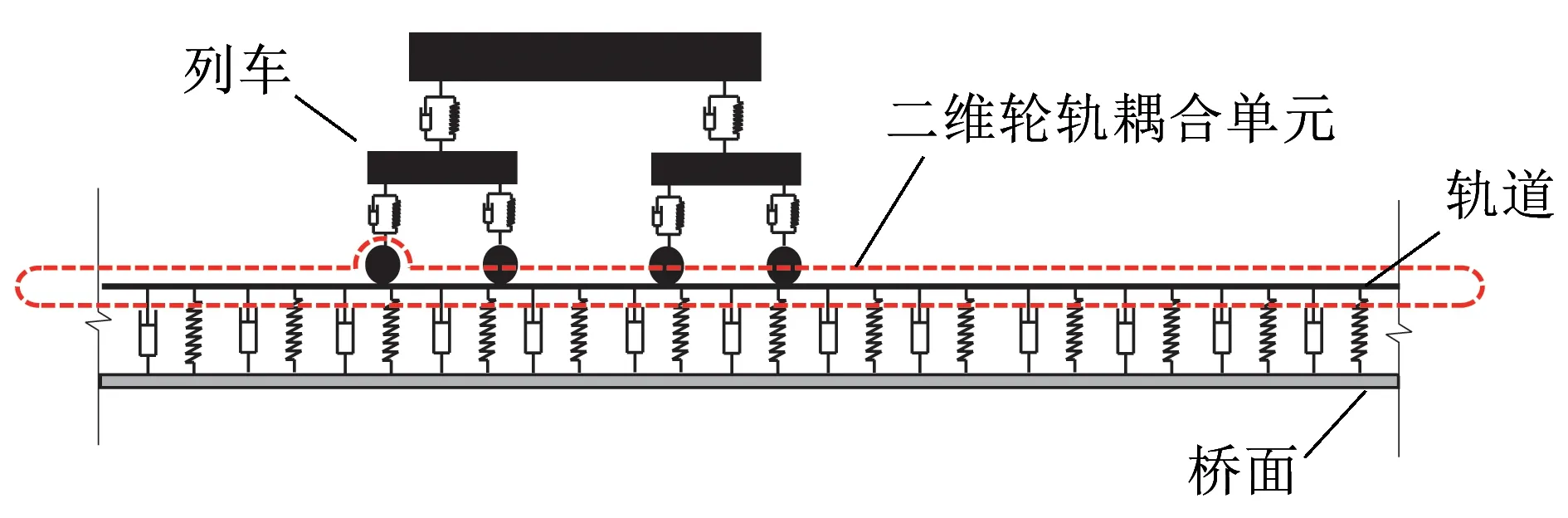
(a)車-軌-橋系統模型
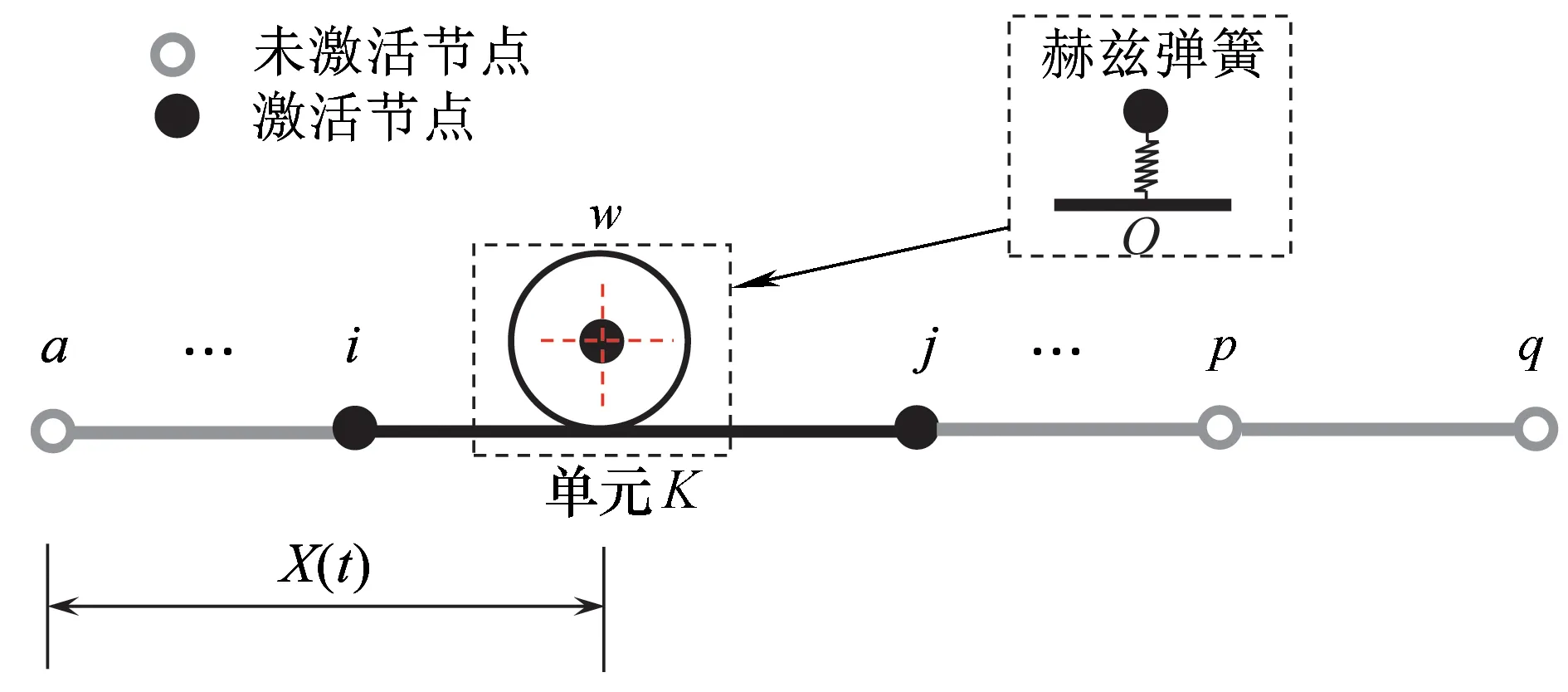
(b)二維輪軌耦合單元模型圖1 二維輪軌耦合單元模型及所在位置示意
對于二維問題,忽略軌道梁水平方向的自由度,梁單元僅考慮豎向和轉動自由度,車輪僅考慮豎向自由度,因此,二維輪軌耦合單元自由度和內力可表示為
( 1 )
( 2 )
式中:u1為車輪節點豎向位移;R1為車輪節點豎向內力;u2~un為所有可能與車輪接觸的梁單元節點位移;R2~Rn為所有可能與車輪接觸的梁單元節點內力。
如圖1(a)所示,在某一時刻t,車輪行進至單元K處時,二維輪軌耦合單元a、p、q節點內力和對應剛度取值均為0,i、j節點內力和對應剛度取值不為0。因此,為方便推導計算,我們將非接觸處的局部節點a、p、q定義為未激活節點,接觸處單元K的局部節點i、j定義為激活節點。因此,激活的局部輪軌耦合單元自由度和節點內力定義為
( 3 )
( 4 )
如圖2所示,u2~u5和R2~R5分別表示局部輪軌耦合單元激活節點對應的位移和內力。
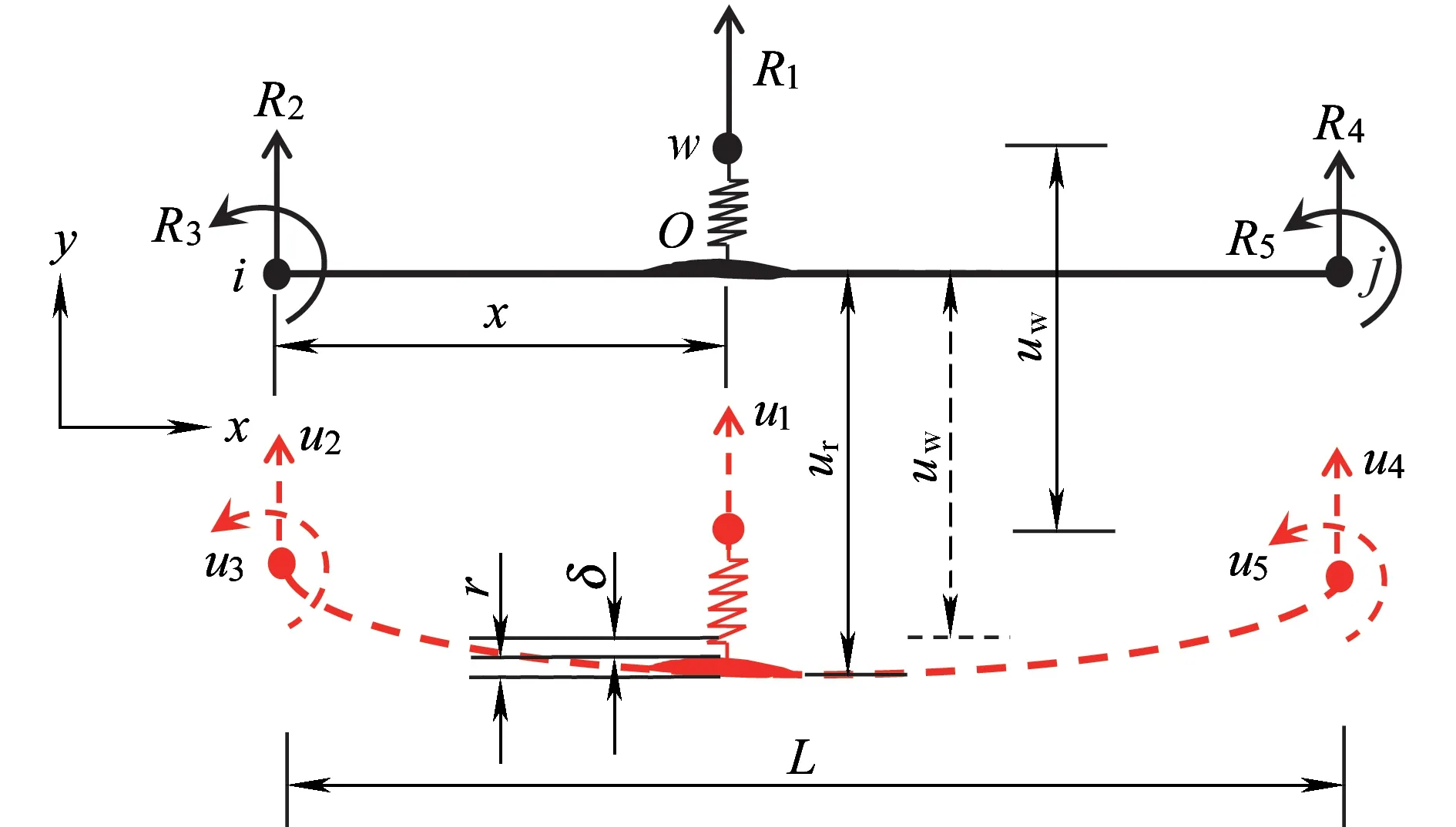
圖2 激活的輪軌耦合單元局部節點
1.1 輪軌接觸力直接求解
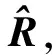
( 5 )
其中
如圖2所示,x為輪節點w與激活的輪下軌道梁左節點i之間的水平距離,可通過X(t)求得;L為輪下梁單元長度。
本文基于赫茲非線性彈性接觸理論,如圖1(b)所示,假定車輪與軌道通過赫茲非線性彈簧連接。當赫茲彈簧剛度取值偏大時,輪軌間相對位移微小,即可將輪軌之間的連接近似為剛性桿連接,模擬密貼接觸的情況;當赫茲彈簧取值正常時,輪軌之間的連接視為正常的彈性接觸狀態,因此可同時考慮輪軌間嵌入和分離兩種情況。輪軌之間豎向作用力與嵌入量的關系[1]為
( 6 )
式中:G為輪軌接觸常數,m/N3/2,本文選取錐形踏輪面,計算參數表達式為
G=4.57R-0.149×10-8
( 7 )
其中,R為車輛半徑,m;δ為輪軌接觸處赫茲彈簧壓縮量,δ>0為輪軌間存在嵌入量,δ≤0為輪軌脫離。
由赫茲力計算式( 6 )可知,輪軌間赫茲彈簧變形量δ是計算輪軌作用力FH的基礎。接觸幾何關系如圖2所示,本文通過車輪節點和輪軌接觸處梁單元節點之間的位移差及軌道不平順值計算輪軌接觸處赫茲彈簧壓縮量δ。
δ=ur-uw+r
( 8 )
式中:uw為車輪位移;r為接觸點處軌道不平順值;ur為接觸點處軌道梁的位移,包含由形函數插值得到的位移,也包含由于輪軌相互作用產生的位移
ur=us+uH
( 9 )
式中:us為插值得到的輪下軌道梁的位移
(10)
uH為赫茲力作用產生的位移
(11)
式中:Kb為梁的柔度。
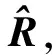
輪軌作用力FH求解步驟如下:
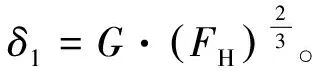
步驟2依據式( 8 )、式( 9 )計算輪軌嵌入深度δ2=ur-uw+r=us+uH-uw+r。
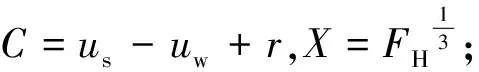
步驟4更新車輪位置,判斷車輪是否在單元兩端(圖3),構造解的形式。
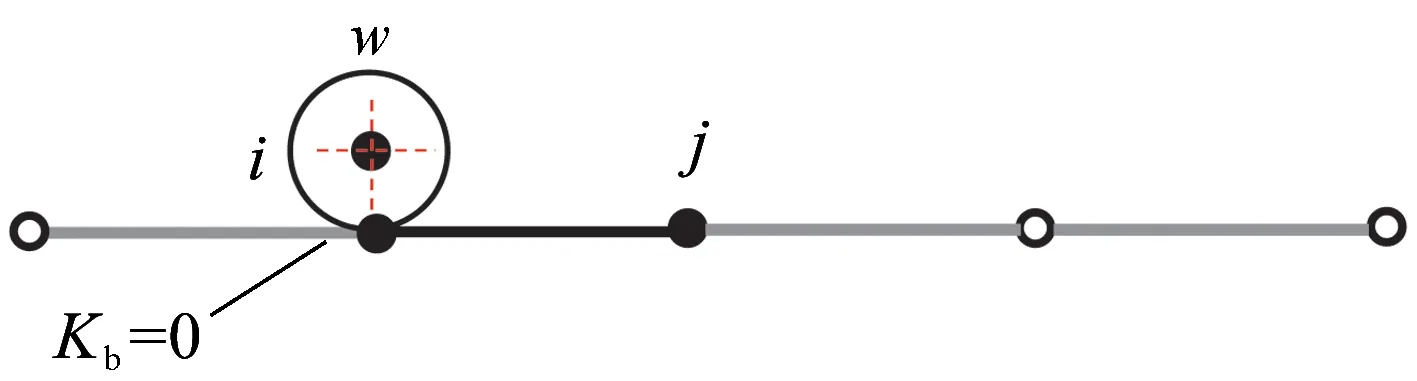
(a) 車輪位于梁單元端部
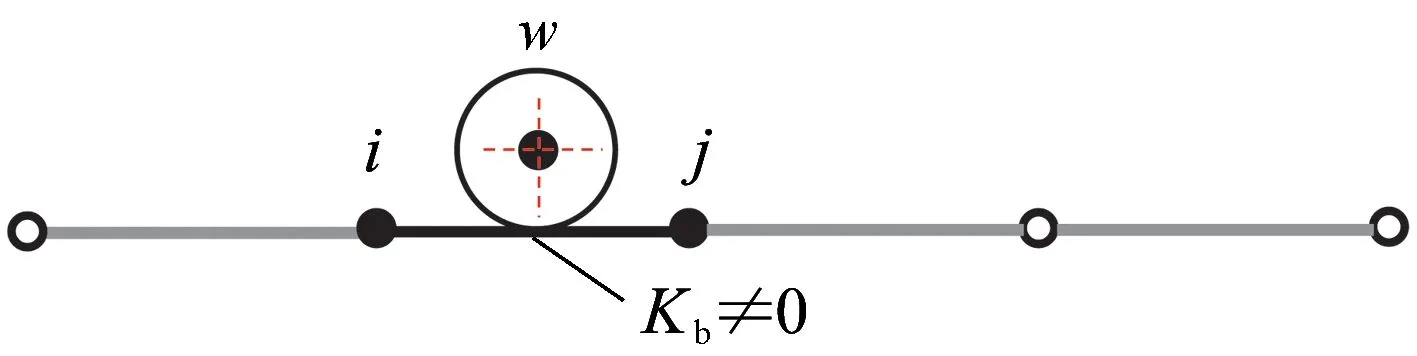
(b)車輪位于梁單元內部圖3 車輪位置示意
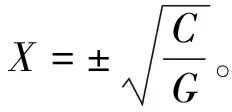
(2)若在單元內部,則Kb≠0,方程為KbX3+GX2-C=0;方程改寫為aX3+bX2+d=0。
①計算一元三次方程求解參數
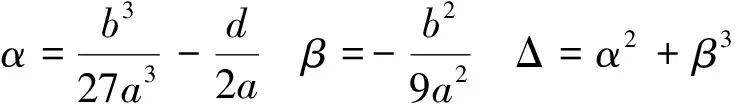
②若Δ≥0且α=0,有實數解
③若Δ=0且α≠0,有兩個不同實數解
④若Δ<0,有3個實數解
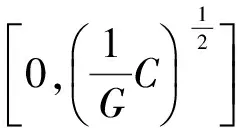
1.2 單元剛度推導
(12)
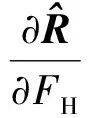
(13)
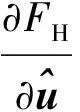
φ=δ1-δ2
(14)
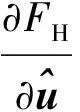
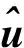
(15)
(16)
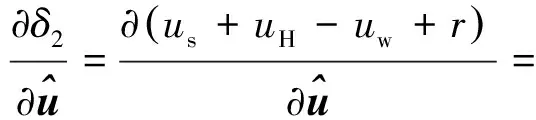
(17)
將式(16)、式(17)代入式式(15)可得
(18)
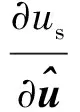
(19)
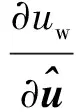
(20)
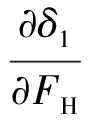
(21)
由式(11)可得赫茲力作用下輪下軌道梁的位移uH與FH的關系
(22)
將式(19)~式(22)代入式(18)中可得
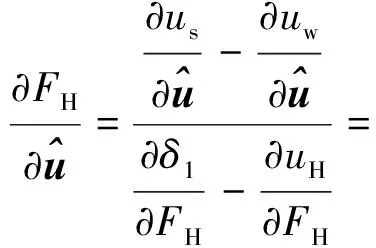
(23)
將式(13)和式(23)代入式(12)即可得激活的局部輪軌耦合單元切線剛度表達式
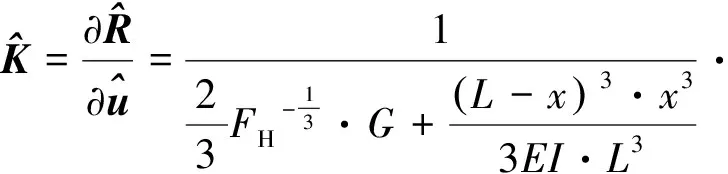
(24)
2 數值驗證
為驗證本文所提輪軌耦合單元模型的可靠性,進行數值驗證。如圖4所示,質塊近似模擬車輛車體,簡支梁模擬橋梁,質塊與簡支梁之間通過彈簧連接,忽略車輪質量。參數取值[11]如下:質塊滑動速度為vc=27.78 m/s,加速度為ac=0 m/s2,簡支梁跨度Lb=30 m,彈性模量Eb=2.87×109Pa,截面慣性矩Ib=2.9 m4,阻尼比ζb=0,橋梁線密度mb=2 303 kg/m,質塊質量mb=5 750 kg,車輪質量mw取0,連接彈簧阻尼cv=0.0 N·s/m,剛度kv=1.595×106N/m。
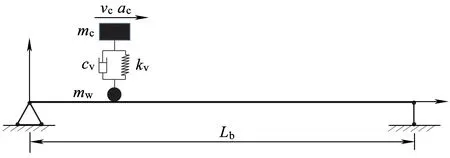
圖4 移動質量作用下的簡支梁模型
簡支梁采用兩個二維彈性梁柱單元模擬,不考慮軌道不平順的影響,將本文分析模型計算所得質塊豎向位移dm、加速度am和簡支梁跨中撓度db時程曲線與文獻[11]對比。如圖5~圖7所示,基于輪軌耦合滑動單元的有限元模型計算所得的質塊豎向位移、豎向加速度和簡支梁跨中位移時程曲線與文獻[11]中3階模態解析解(圖中標注為解析解)和數值解(圖中標注為數值解)非常接近。由于解析解僅考慮了3階模態,所以時程曲線局部有微小差別。綜上可知,本文提出的單元模型可靠,滿足工程精度要求。
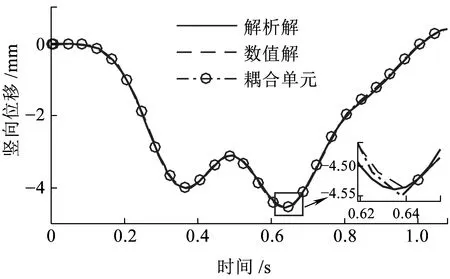
圖5 質塊豎向位移時程
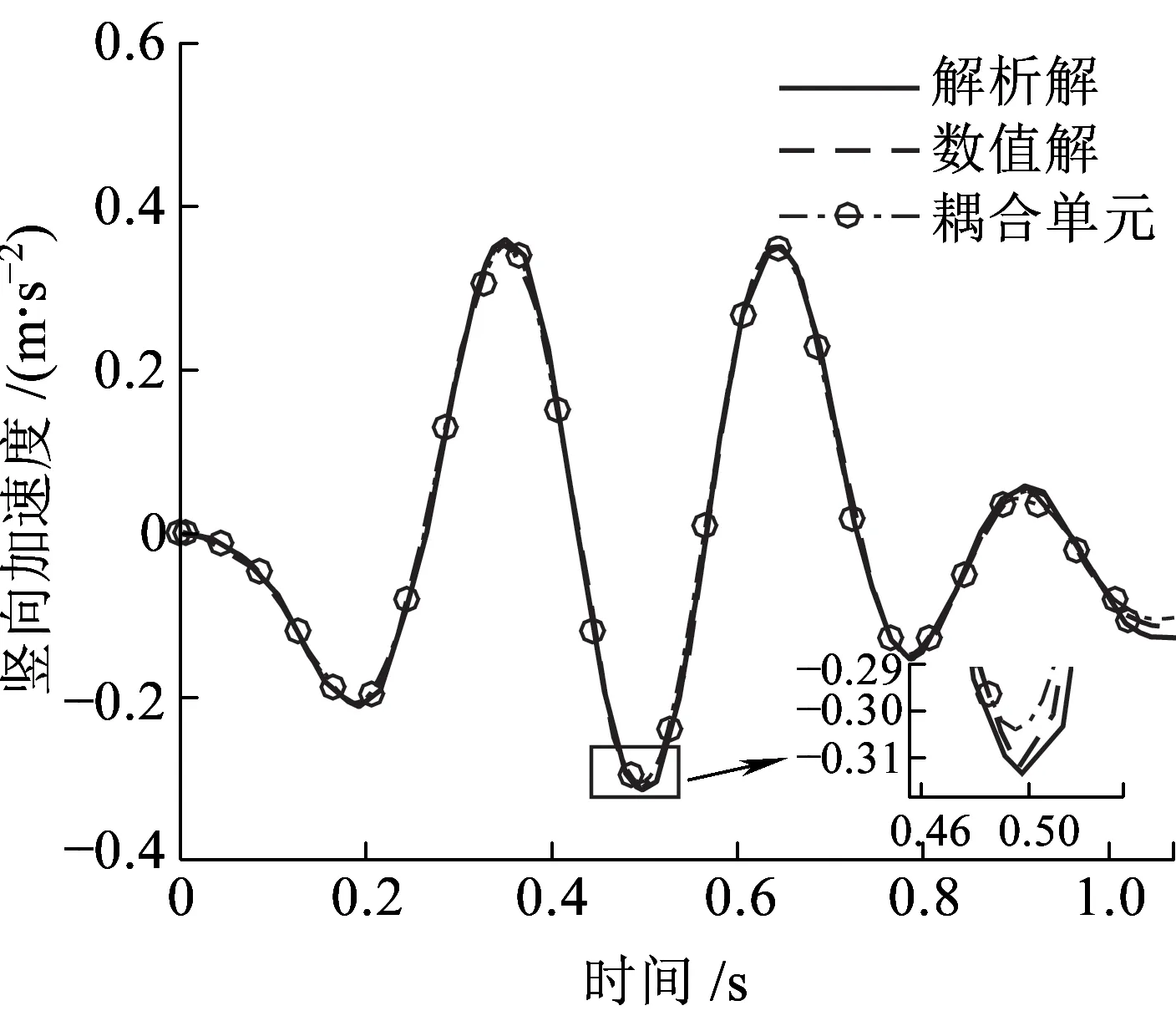
圖6 質塊豎向加速度時程
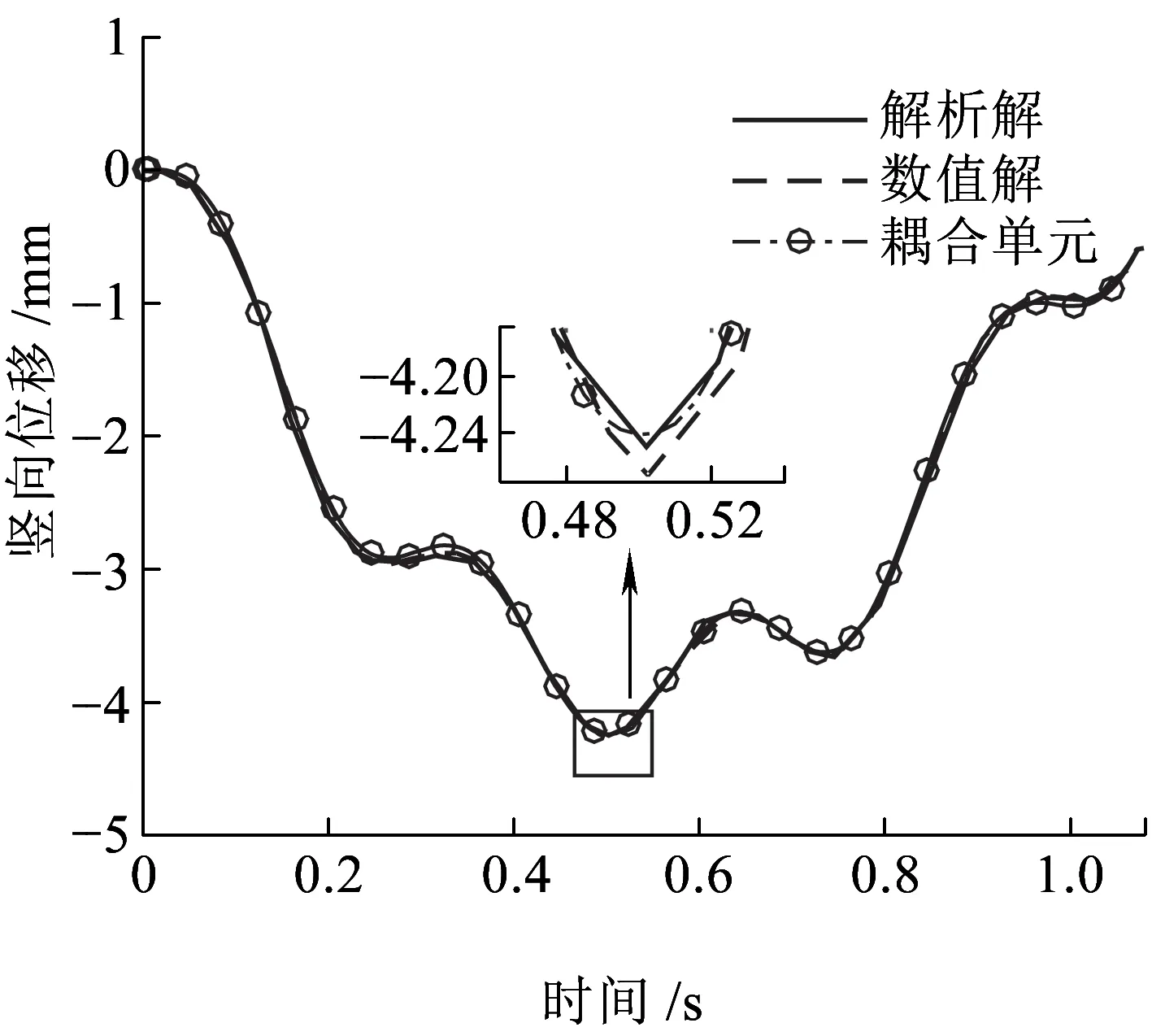
圖7 簡支梁跨中位移時程
3 車橋系統地震響應分析
本文利用OpenSees豐富的材料庫和單元庫,將車輛子系統和軌道-橋梁子系統通過OpenSees建模,輪軌耦合系統由本文提出的二維輪軌耦合單元建模,完成豎向車橋耦合系統模型建立。
3.1 車輛系統模型
如圖8所示,車輛系統考慮為四軸多剛體體系,該車輛模型由1個車體、2個轉向架、4個輪對構成,車輪與轉向架間由一系彈簧ktw和阻尼器ctw連接,車體與轉向架間由二系彈簧kct和阻尼器cct連接。車體和轉向架有沉浮和點頭兩個自由度,車輪只有沉浮自由度,因此,車輛系統共有10個自由度。建模時,將車體和轉向架考慮為剛體,選用兩個彈性梁柱單元進行模擬,抗彎剛度取無限大值;車體和轉向架之間通過車體端部節點和轉向架中部節點連接,選用桁架單元進行模擬。車輛參數[11]見表1。
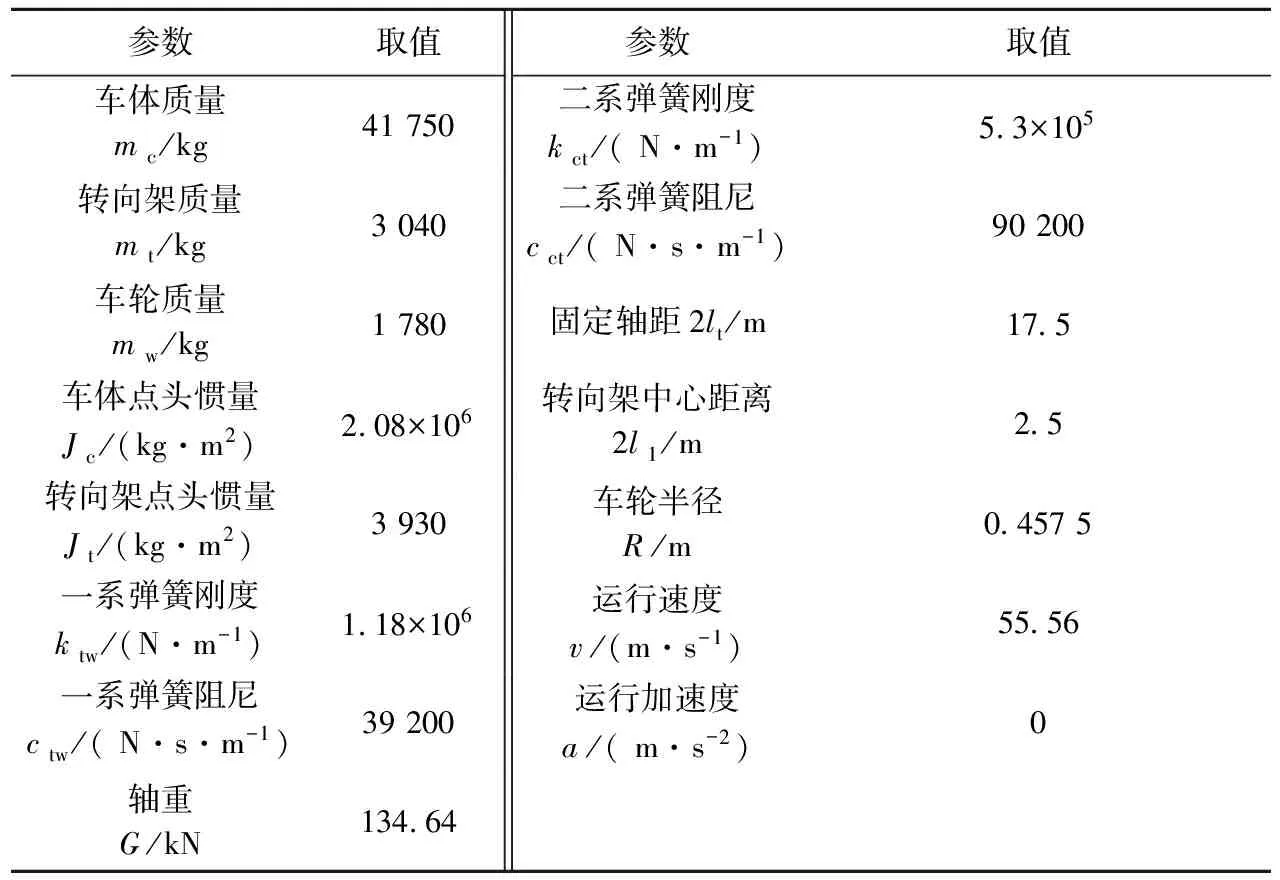
表1 車輛系統參數
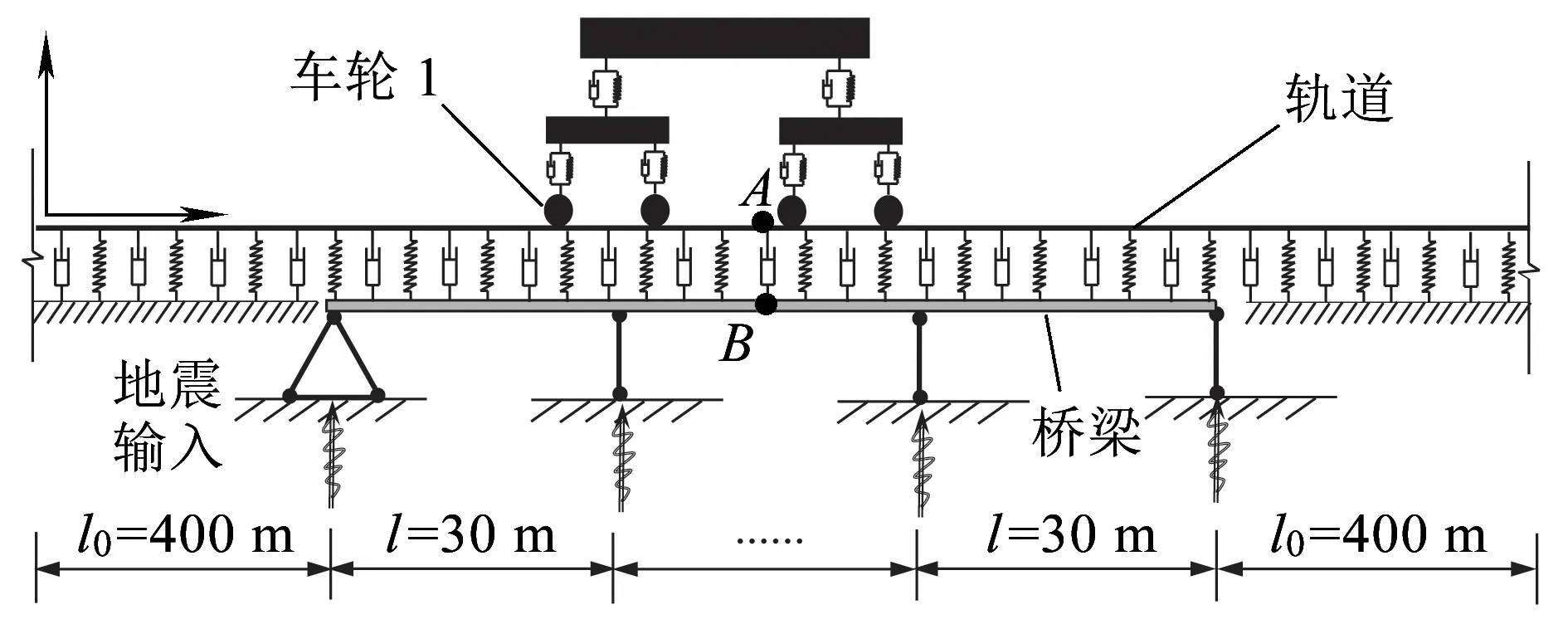
圖8 豎向車橋相互作用系統示意
3.2 軌道-橋梁系統模型
如圖8所示,在軌道-橋梁系統中,軌道全長1 130 m,橋梁簡化為11跨連續梁,單跨長度為30 m。鋼軌中部由11跨連續梁支撐,前后端由剛性路基支撐。將軌道與地基、橋梁間的相互作用簡化為線性彈簧和阻尼器連接,詳細參數[11]見表2。
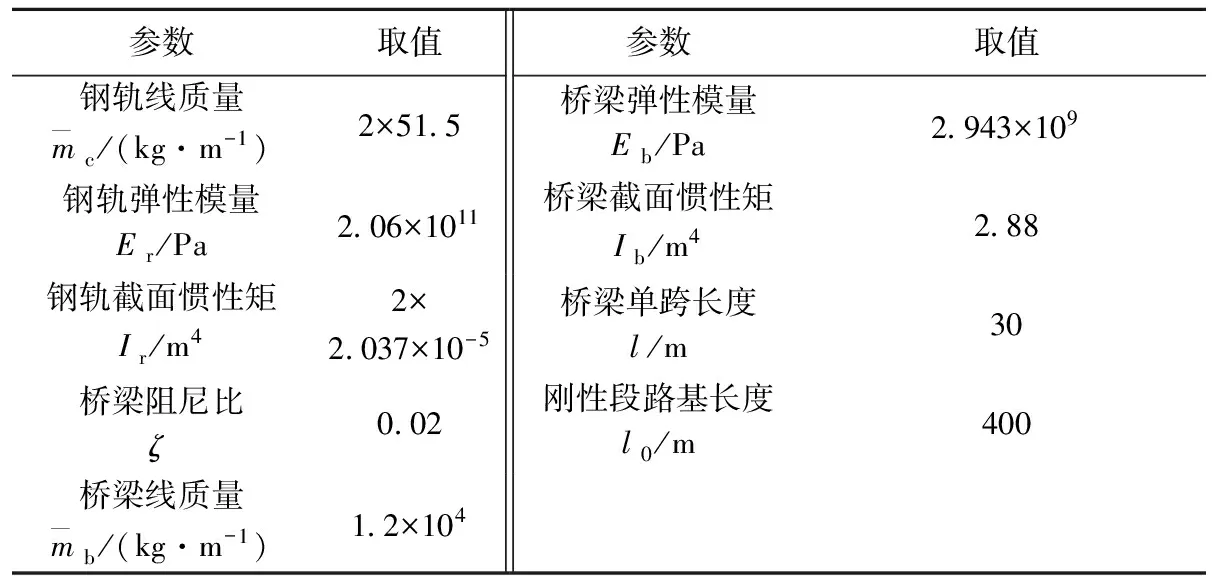
表2 軌道-橋梁系統參數表
3.3 軌道不平順激勵和地震激勵輸入
本文除考慮自重作用外,還將考慮軌道不平順激勵和地震激勵的影響。軌道不平順r通過式( 8 )方式輸入,即將軌道不平順考慮為輪軌接觸處赫茲彈簧變形量的一部分。
(25)
將El Centro地震波豎向加速度作為地震激勵作用在軌道梁支承部分,忽略土和結構相互作用,El Centro地震豎向波時程曲線如圖9所示,絕對加速度反應譜如圖10所示。
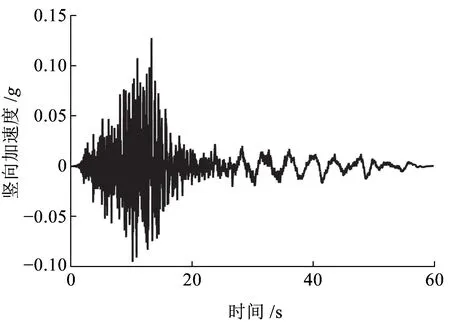
圖9 El Centro地震波豎向加速度時程曲線
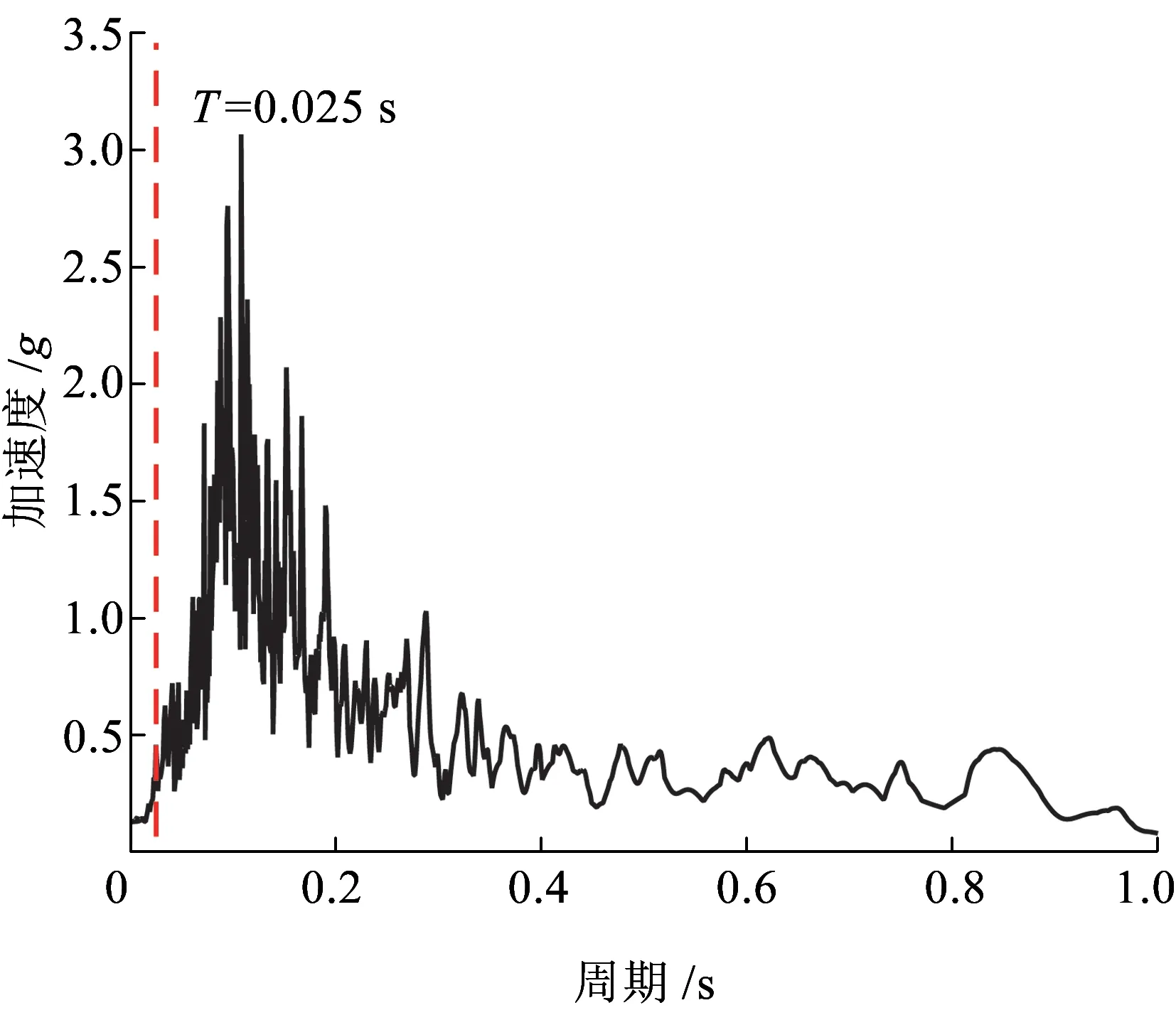
圖10 El Centro地震波豎向加速度反應譜
3.4 計算結果分析
本文將車輪1(圖8)與軌道作用力(赫茲力)作為車橋動力相互作用強弱的特征指標,為對比動力放大與縮小效應,進一步將該相互作用考慮為赫茲力與車體單軸軸重之比。將鋼軌中點A(圖8)、橋梁第六跨中點B(圖8)及車體的位移和加速度時程曲線作為列車-軌道-橋梁系統動力響應評價,其中,系統位移響應均為消除靜力平衡位移后的豎向位移。
列車整車開始通過到離開11跨連續梁的總時間為6.3 s,為了節約篇幅,本文僅選取車輪1(圖8)經過軌道不平順時段(3.32~3.34 s)作為動力響應評價依據,考慮四種工況進行分析,見表3。

表3 計算工況
圖11為輪軌作用力與軸重比例系數時程曲線,觀察可知,工況Ⅰ和工況Ⅲ的時程曲線基本重合;類似地,工況Ⅱ和工況Ⅳ也基本重合;兩組工況下輪軌作用力差異較大。表現為:當車輪1遇到軌道不平順時(3.32~3.35 s),輪軌作用力突然增至軸重的約2倍。軌道平順時,輪軌作用力增減幅度保持在軸重的10%以內,地震作用影響較小。由于豎向輪軌相互作用系統(赫茲彈簧)的第一階自振頻率約為40 Hz(T=0.025 s),大于所選El Centro波的主要頻率(圖9),因此,相比地震作用,軌道不平順激勵對豎向輪軌相互作用的影響更明顯。
圖12為第6跨橋梁跨中B點豎向位移時程曲線,觀察可知,工況Ⅰ和工況ⅡB點豎向位移時程曲線基本重合;類似地,工況Ⅱ和工況Ⅳ也基本重合,兩組工況下位移差異較大。這表明,地震作用對B點豎向位移影響明顯,相反,軌道不平順激勵作用對其影響較小。圖13為第6跨橋梁跨中B點豎向加速度時程曲線,觀察可知,四種工況下B點豎向加速度時程曲線幅值有較大差異,峰值由大到小依次為:工況Ⅳ、工況Ⅲ、工況Ⅱ、工況Ⅰ。由此可知,B點豎向加速度對軌道不平順激勵和地震作用都很敏感,軌道不平順激勵會進一步增大B點加速度幅值。
圖14為軌道中點A豎向位移時程曲線,觀察可知,四種工況下A點豎向位移時程曲線幅值有較大差異。這表明,軌道不平順激勵和地震作用對A點豎向位移影響明顯,軌道不平順激勵會改變A點位移幅值。圖15為軌道中點A豎向加速度時程曲線,觀察可知,工況Ⅰ和工況Ⅲ的A點豎向加速度時程曲線基本重合;類似地,工況Ⅱ和工況Ⅳ也基本重合,兩組工況下加速度差異較大。由此可知,地震作用對A點豎向加速度影響較小,而軌道不平順激勵則影響明顯。
圖16、圖17為車體質心豎向位移和加速度時程曲線,觀察可知,工況Ⅰ和工況Ⅱ下的車體豎向位移和加速度時程曲線基本重合;類似地,工況Ⅲ和工況Ⅳ也基本重合;兩組工況下車體動力響應差異較大。進一步觀察表明,在沒有地震時車體的位移和加速度都較小。地震作用對車體質心豎向位移影響明顯,軌道不平順激勵的影響較小。地震作用和軌道不平順激勵對車體質心豎向加速度均有影響,但地震作用影響更明顯。
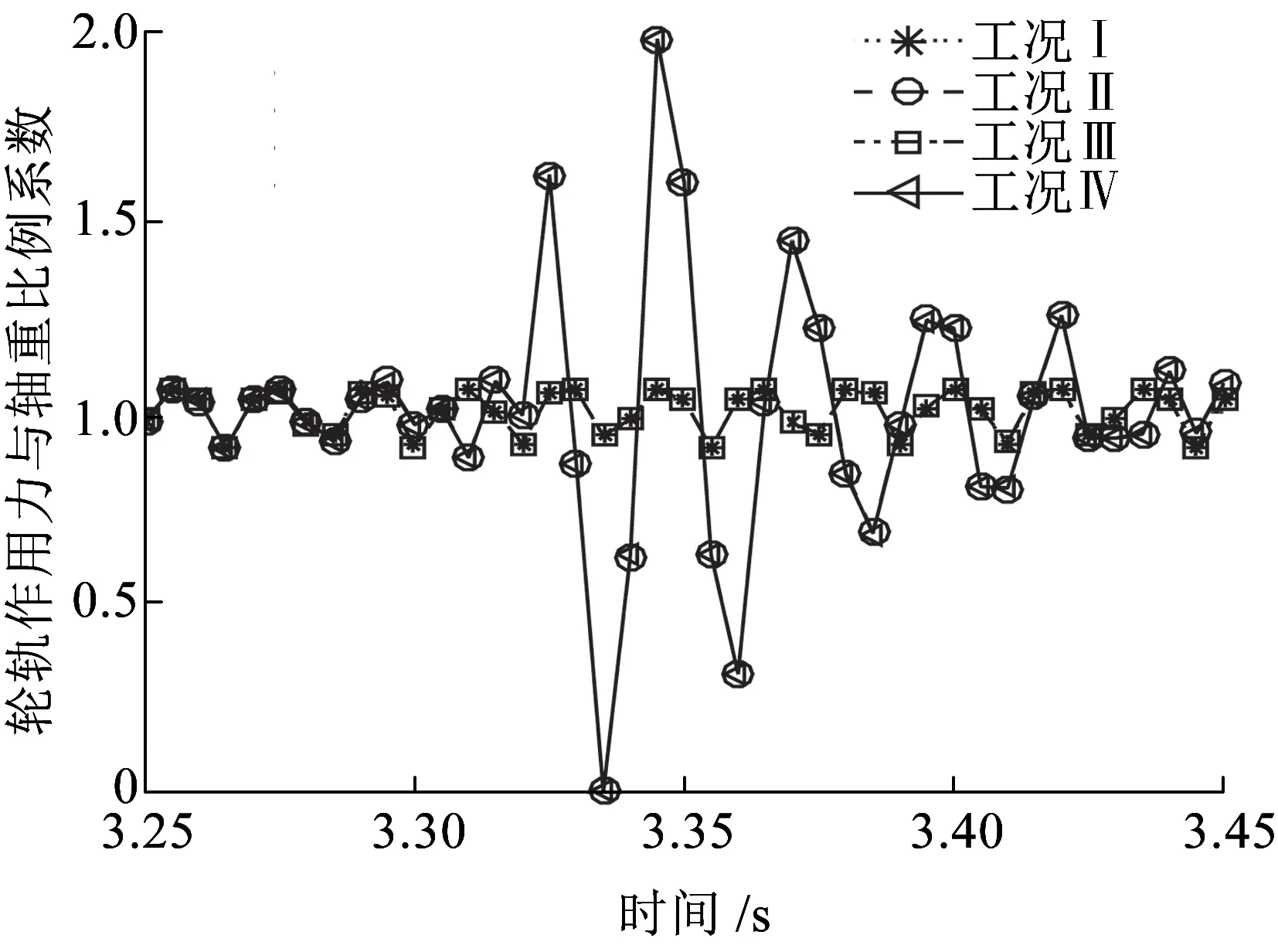
圖11 作用力與軸重比例系數時程曲線

圖12 第6跨橋梁跨中B點豎向位移時程曲線
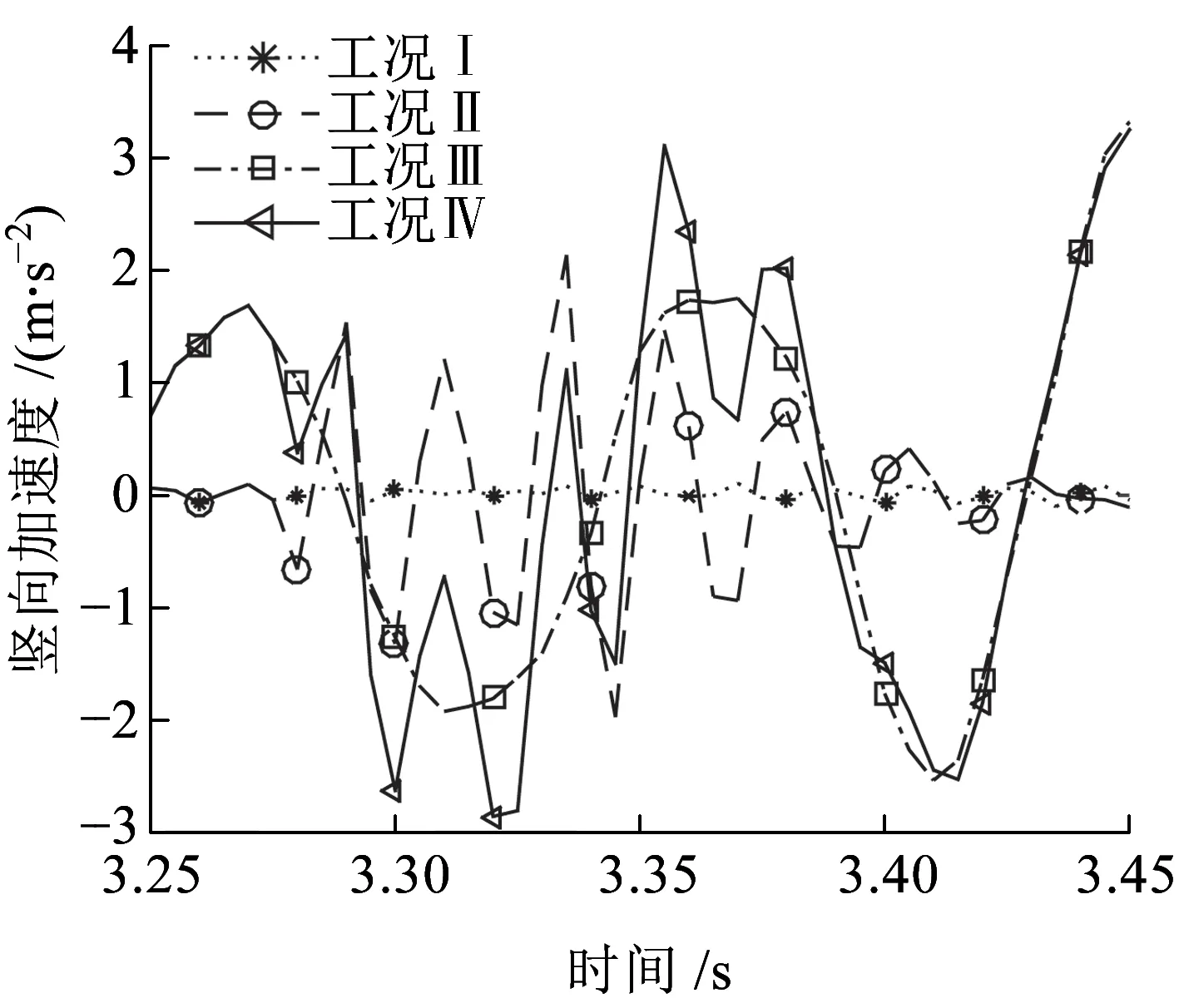
圖13 第6跨橋梁跨中B點豎向加速度時程曲線
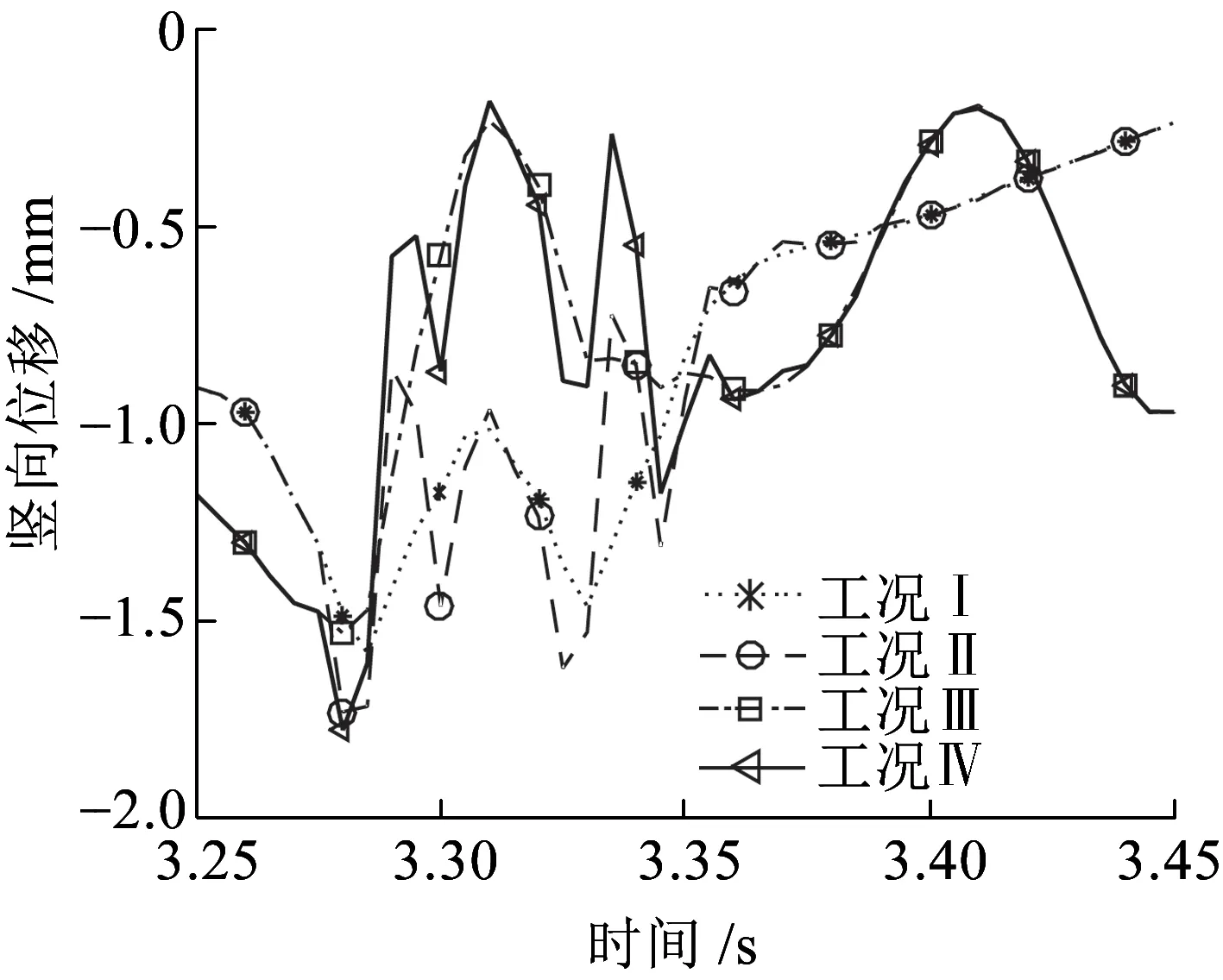
圖14 軌道中點A豎向位移時程曲線
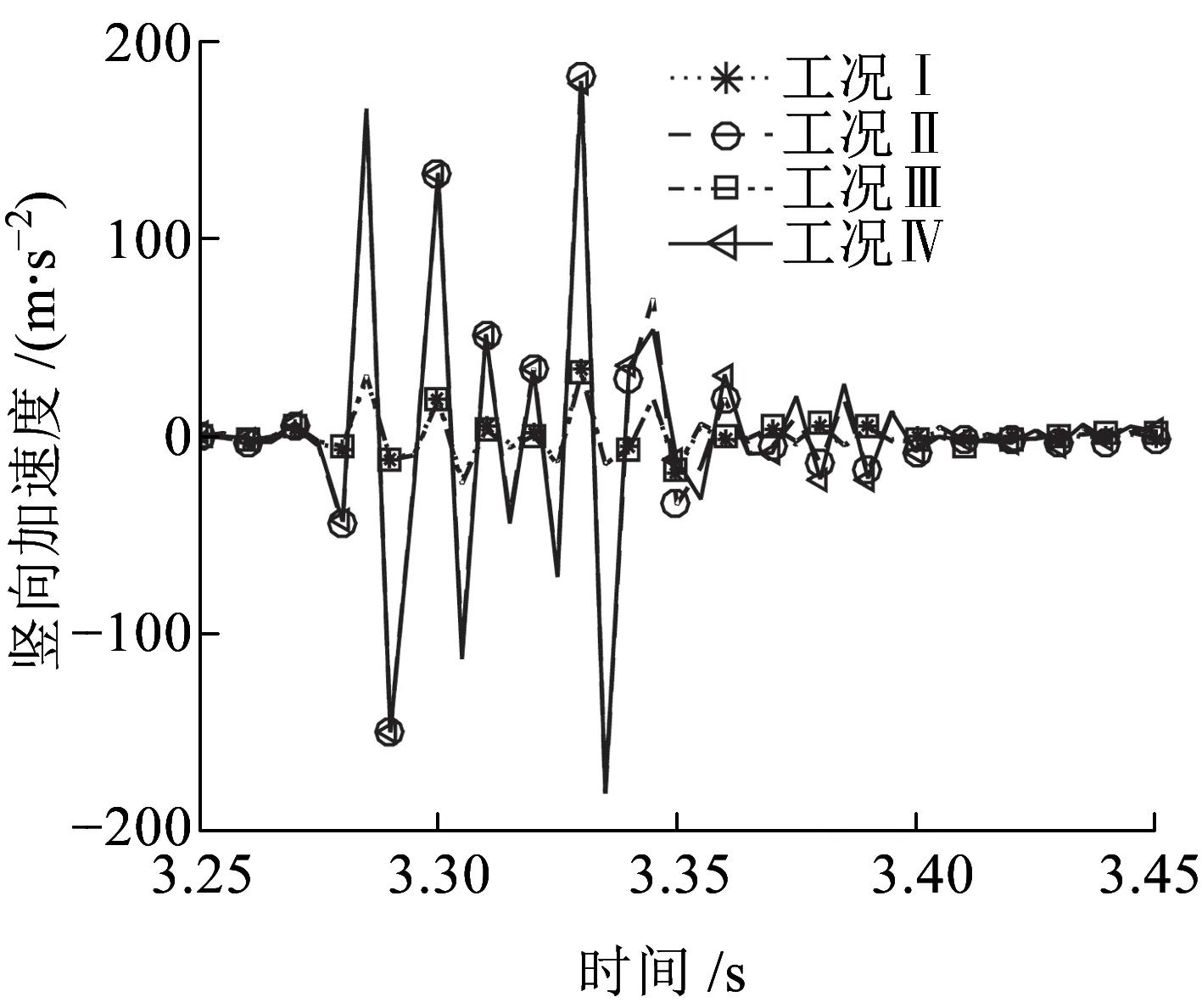
圖15 軌道中點A豎向加速度時程曲線
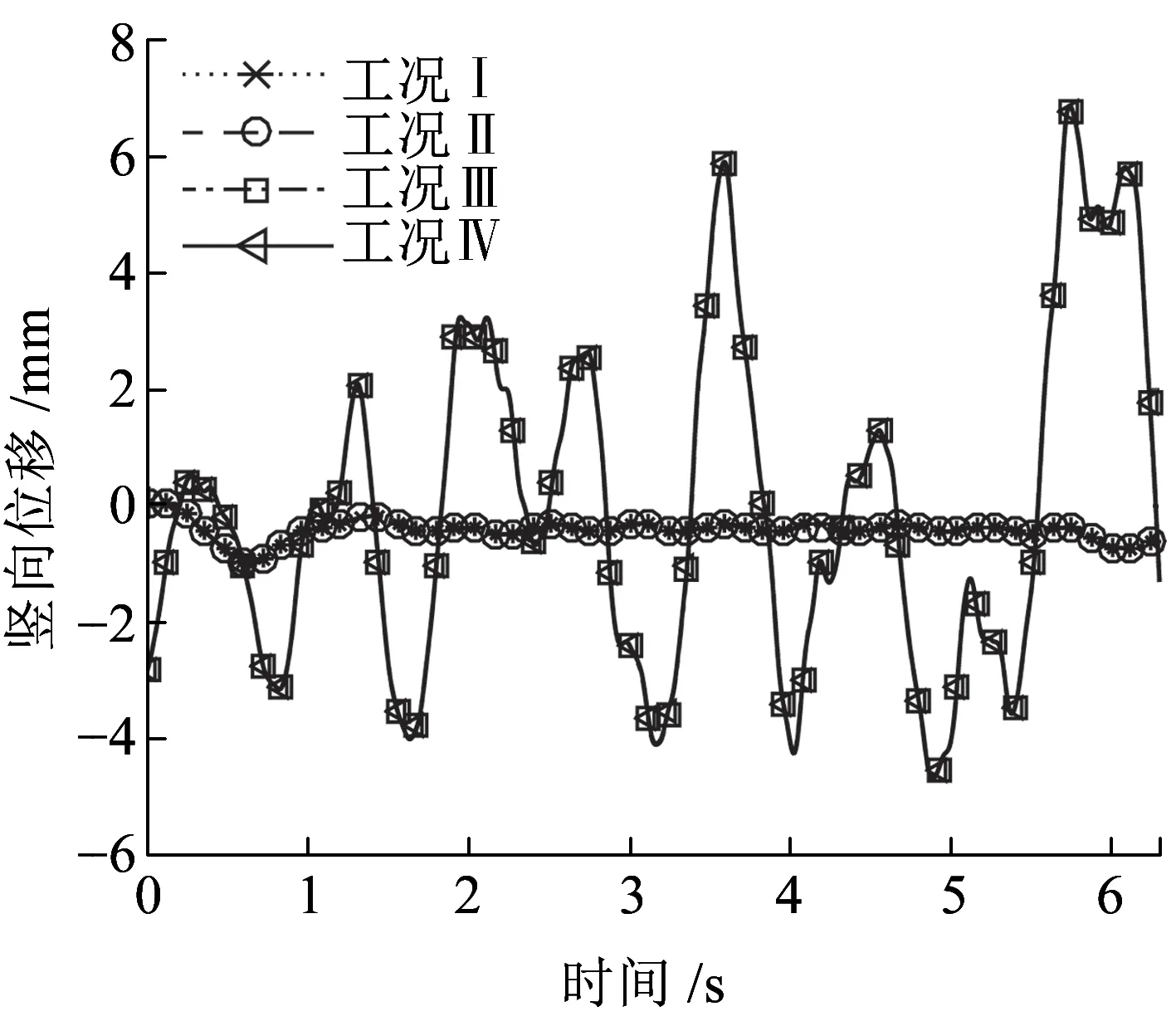
圖16 車體質心豎向位移時程曲線
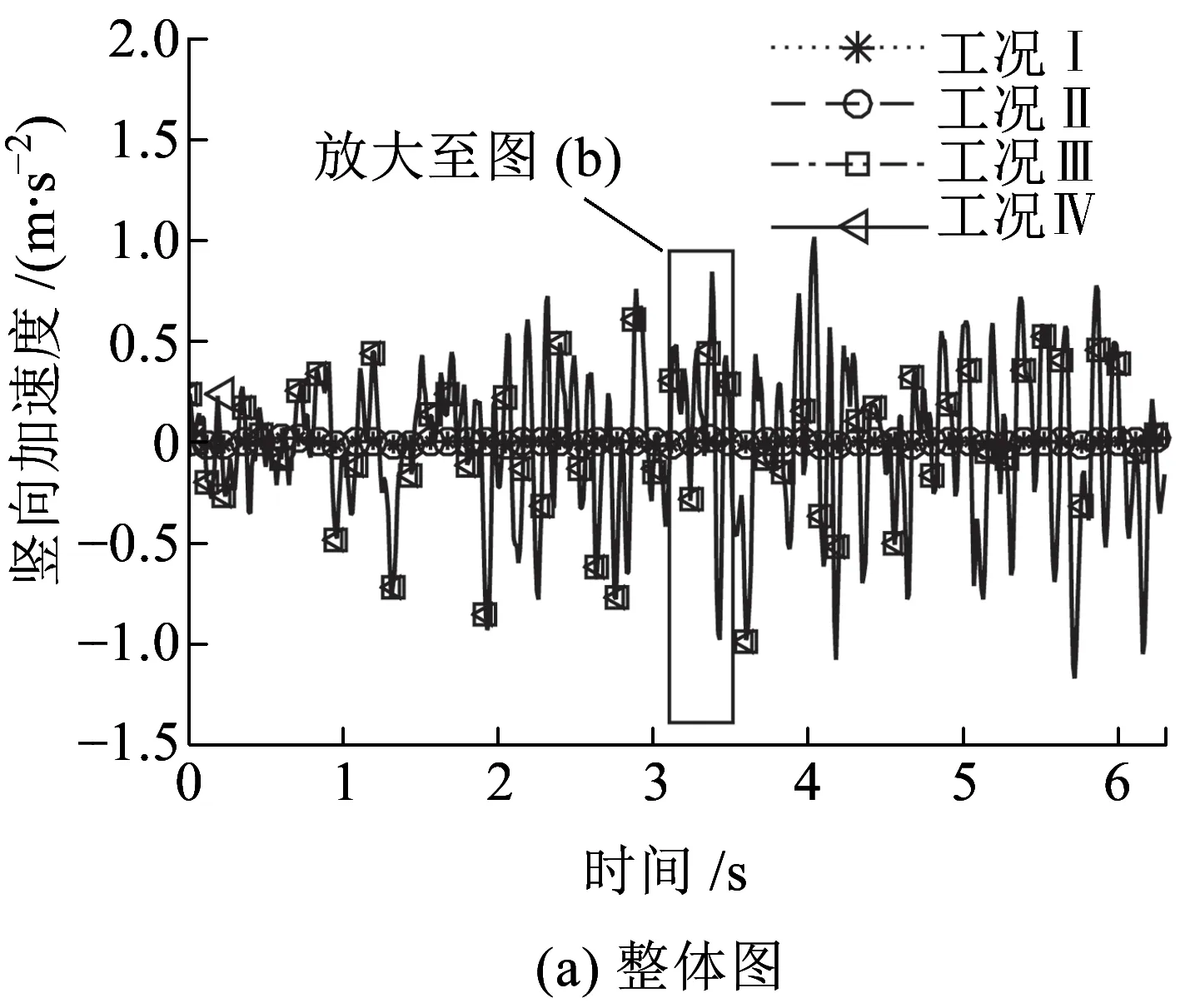
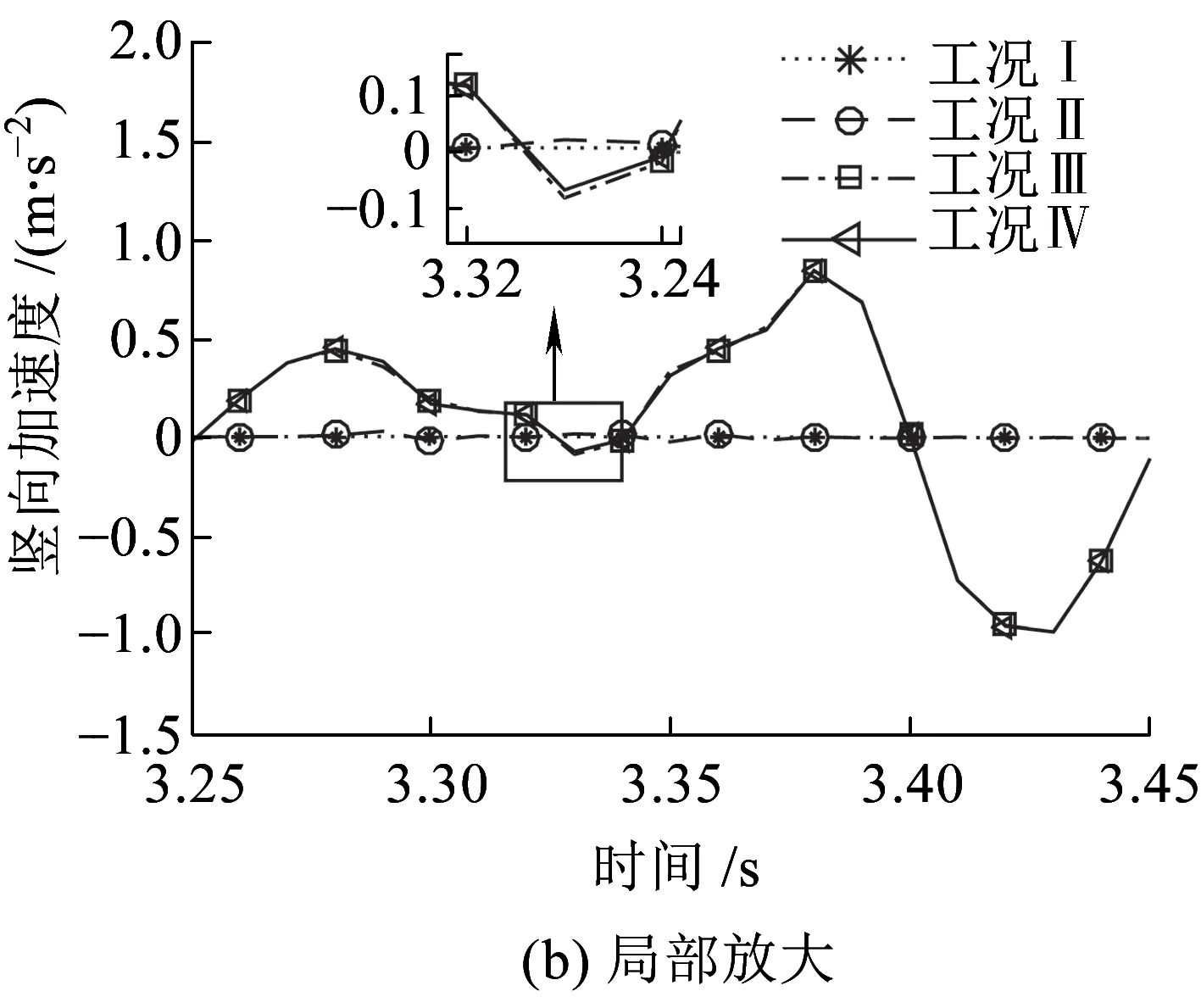
圖17 車體質心豎向加速度時程曲線
4 結論
本文提出一種基于非線性接觸關系的新型二維輪軌耦合單元。該單元僅考慮輪軌相互作用,單元節點由一個輪節點和列車行進過程中所有可能與之接觸的梁單元節點序列組成。通過建立和求解輪軌接觸力滿足的一元三次方程,得到輪軌之間的接觸力,計算由輪軌相互作用產生的耦合單元節點力,最后推導了二維輪軌耦合單元剛度。基于此單元模型,本文建立豎向車橋耦合系統有限元模型并進行地震動力分析。該單元模型有如下優勢:(1)易于集成到現有的通用有限元框架,編程難度小;(2)車輛運行中有限元模型無需修改,建模難度小;(3)能夠模擬輪軌間非線性接觸,可考慮車輛跳軌和軌道不平順激勵的影響。
本文將新型二維輪軌耦合單元模型與列車、軌道和橋梁模型聯合使用,分析了豎向車橋系統在軌道不平順和地震作用同時存在時的動力響應問題,得出如下結論:
(1)地震作用對車體質心豎向位移影響明顯,軌道不平順激勵影響較小。地震作用和軌道不平順激勵對車體質心豎向加速度均有影響,但地震作用影響更明顯。
(2)與地震作用相比,軌道不平順激勵對豎向輪軌相互作用的影響更明顯。
(3)軌道不平順激勵和地震作用對軌道位移影響明顯,軌道不平順激勵會改變鋼軌位移幅值。軌道不平順激勵對鋼軌加速度影響明顯,地震作用對其影響較小。
(4)地震作用對橋梁豎向位移影響明顯,相反,軌道不平順激勵作用對其影響較小。橋梁豎向加速度對軌道不平順激勵和地震作用都很敏感,軌道不平順激勵會進一步增大加速度幅值。
參考文獻:
[1]翟碗明. 車輛-軌道耦合動力學[M]. 4版. 北京:科學出版社,2015.
[2]夏禾,張楠. 車輛與結構動力相互作用[M]. 2版. 北京:科學出版社, 2005.
[3]YANG Y B, YAN J D, WU Y S.Vehicle-bridge Interaction Dynsmics: With Appliactions to High-speed Railways [M]. Singapore: World Scientific Publishing Co., Pte., Ltd., 2004.
[4]林玉森, 李小珍, 強士中. 車橋耦合振動中2種輪軌接觸模型的比較分析[J]. 中國鐵道科學, 2007, 28(6):70-74.
LIN Yusen, LI Xiaozhen, QIANG Shizhong. Contrast Analysis of Two Wheel-rail Contact Models in the Coupling Vibration of Vehicle-bridge System[J]. China Railway Science, 2007, 28(6):70-74.
[5]YANG Y B, YAU J D. Vehicle-bridge Interaction Element for Dynamic Analysis[J]. Journal of Structural Engineering, 1997, 123(11): 1512-1518.
[6]YANG Y B, CHANG C H, YAU J D. An Element for Analysing Vehicle-bridge Systems Considering Vehicle’s Pitching Effect[J]. International Journal for Numerical Methods in Engineering, 1999,46:1031-1047.
[7]YANG Y B, WU Y S. A Versatile Element for Analyzing Vehicle-bridge Interaction Response[J]. Engineering Structures, 2001, 23(5):452-469.
[8]YANG Y B, WU Y S. Dynamic Stability of Trains Moving over Bridges Shaken by Earthquakes[J]. Journal of Sound and Vibration, 2002, 258(1):65-94.
[9]雷曉燕, 張斌, 劉慶杰. 列車-軌道系統豎向動力分析的車輛軌道單元模型[J]. 振動與沖擊, 2010, 29(3): 168-173.
LEI Xiaoyan, ZHANG Bin, LIU Qingjie. Model of Vehicle and Track Elements for Vertical Dynamic Analysis of Vehicle-track System[J].Journal of Vibration and Shock, 2010, 29(3):168-173.
[10]婁平, 曾慶元. 車輛-軌道-橋梁系統豎向運動方程的建立[J]. 鐵道學報, 2004, 26(5):71-80.
LOU Ping, ZENG Qingyuan. Formulation of Equations of Vertical Motion for Vehicle-track-bridge System[J]. Journal of the China Railway Society, 2004, 26(5):71-80.
[11]LOU P, ZENG Q Y. Formulation of Equations of Motion of Finite Element Form for Vehicle-track-bridge Interaction System with Two Types of Vehicle Model[J]. International Journal for Numerical Methods in Engineering, 2005, 62(3):435-474.
[12]BOWE C J, MULLARKEY T P. Wheel-rail Contact Elements Incorporating Irregularities[J]. Advances in Engineering Software, 2005, 36(11/12):827-837.
[13]劉常亮, 尹訓強, 林皋,等. 基于ANSYS平臺的高速列車-軌道-橋梁時變系統地震響應分析[J]. 振動與沖擊, 2013, 32(21):58-64.
LIU Changliang,YIN Xunqiang,LIN Gao,et al. Seismic Response Analysis of a Time-varying High Speed Train-rail-bridge System Based on ANSYS[J].Journal of Vibration and Shock, 2013, 32(21):58-64.
[14]MAZZONI S, MCKENNA F, SCOTT M H, et al. Open System for Earthquake Engineering Simulation (OpenSEES) Opensees Command Language Manual[M]. California:University of California, 2006.

