集對分析在年降雨量預測方面的分析和應用

萬 陽

(重慶市烏江電力有限公司，重慶 409000)

0 前 言

降雨是自然界水循環過程中的重要一環，是自然界中徑流來源的主要因素。降雨量的多少對自然環境影響不可小覷，降雨過多會造成洪災，降雨過少會造成干旱。若可提前預估來年的降雨情況，并以此作為未來1年的工作規劃依據，充分利用來年雨水資源，在干旱時就可減輕災害，在降雨過多時提前做好應對準備，大大減輕雨水災害造成的損失。在水文分析與預測預報中，首要的工作就是對降雨進行科學的預測。降雨量預測方法有線性分析方法和非線性分析方法，其中非線性分析方法有自回歸模型，人工神經網絡、灰色模型、集對分析、模糊分析等不確定水文分析方法[1]。近年來，集對分析方法被應用到水文預報當中，預報效果良好。歐源[2]等利用秩次集對分析建立年徑流預測模型，預測岷江紫坪鋪的年徑流量，并和自回歸模型和BP模型的預測結果比較，得出秩次集對模型預測精度較高。劉銀迪[3]等利用序位集對分析對遼河流域的年降雨量進行預測，預報結果較可靠。許美玲[4]等將集對分析運用于云南強降雨過程預報，用權重法將不同強降雨預報進行集成，從而給出集不同預報于一體的云南強降雨預報過程。王紅芳[5]等構建了基于集對分析的最近鄰抽樣年徑流預測模型，并和模糊優選預測結果進行了對比。萬星6]等構建了基于聯系度的水文徑流量狀態預測模型，以水庫總流量和相關氣象要素進行分類，在未來給定因素情況下，運用模型判斷未來流量變化所處位置，進行預測水庫流量。馮利華[7]等基于集對分析來研究預測未來水資源變化情勢，通過變化運用，可以使集對分析具有預測功能。

大部分水文要素之間都有“關系”，例如降雨-徑流、水位-流量、洪峰-洪量。2個水文變量之間的相關關系有正相關、負相關和差異性，而傳統方法采用一個數值來體現水文變量之間的關系，如模糊分析以隸屬度來度量二者之間的關系、灰色原理以灰關聯度來衡量相關關系等，具有一定的局限性，沒法完整描述變量之間的相關性結構[8]。1989年趙克勤基于馬克思哲學理論中的“對立統一觀點”，提出來集對分析方法(Set Pair Analysis，SPA)[9]。集對分析方法基于集對的建立，同時對集對的同一性、差異性和對立性進行分析，并用聯系度來度量集對之間的關系，較科學系統地描述了集對間的關系結構[10]。因此，本文運用集對分析法構建了不同的年降雨量預測模型，并將預測結果進行了對比，優選出最佳的預測方法。

1 P-SPA預測模型

1.1 集對分析原理

集對分析是一種分析不確定性問題的系統分析方法。它綜合考慮同一性、差異性和對立性，局部性和整體性之間的關系，最后以聯系度來衡量同異反程度。這種綜合不確定度能夠較好地描述多種不確定性因素之間的關系結構，避免了單一化指標分析法帶來的誤差。其核心思想就是先對任意有關聯的2個集合A和B構造集對(A，B)，按一定原則對集對(A，B)的特性進行同一性、差異性和對立性分析，最后用綜合的不確定度(聯系度)來描述，即：

(1)

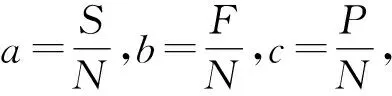
μA-B=a+bi+cj

(2)

式中：a+b+c=1。

1.2 P-SPA集對分析預報模型原理

P-SPA集對分析預報模型的構造方式是確定2個有關聯的集合構造成集對，再對集對的同一性、差異性和對立性進行分析，最后確定集對的異反聯系度，以聯系度的大小來確定2個集對的關系，并以相似預測的原理進行未來情勢的預報。已知年降雨量時間序列為x1,x2,…,xn，且xt與前k個歷史降雨量xt-1,xt-2,…,xt-k存在關系，因此我們可以將已知的年降雨量時間序列滑動生成(n-k+1)個容量為k的集合Ai；每個集合Ai對應著后續值xk+i，見表1所示。若給定一個集合B=(xn-k+1,xn-k+2,…,xn)，其后續值為xn+1，那么我們可以運用集對分析計算集合Ai和集合B聯系度，并優選出相似度高的若干個集合，將其后續值加權或者不加權平均值作為xn+1的預測值。

表1 秩次轉換結果、聯系度及聯系數計算結果表

2 模型求解步驟

(1) 已知年降雨量時間序列為x1,x2,…,xn，構建年降雨量歷史集合Ai及其后續值和集合B，考慮到年降雨量序列的弱相關性，k取值以4～6為宜。

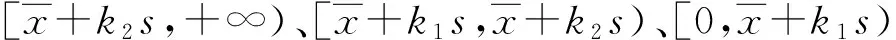
(3) 分別求解集合Ai′和B′的聯系度。秩次變換為將集合Ai′和B′中的元素分別做商，記為fij，當fij=1，則為“同”；當0≤fij<1，為“異”；當fij>1，為“反”。量化變換為將集合Ai′和B′中的元素做差，記為d，當d=0，為“同”；當d=1，為“異”；當d=2，為“反”。給定i、j的數值，分別得到集合Ai′和B′的聯系數。

(4) 根據聯系數最大原則，在集合Ai優選出若干個和集合B相似的集合，優選集合的后續值采用下列公式得到預測值

(3)

式中：m為相似集合的個數。

3 應用實例

以都江堰雨量站1961—2006年共46 a的年降雨量資料為例，將1961—2002年年降雨量資料構建P-SPA集對分析預報模型，預測2003—2006年的年降雨量。經過分析計算，確定預測值與前5年的年降雨量資料有關，采用秩次變換加權集對分析方法。首先以2003年為預測年，預測值對應的集合[1123.4,1213,941.6,1259,992.9]，該集合與構建的37個歷史集合構成37組集對，并將37組集對進行秩次變換，做商求解同一度、差異度和對立度，確定差異不確定分量系數,j取-1，i取0.5，代入式(2)得到37組集對H(Ai，B)的聯系數，如表1所示。

從表1計算結果可以看出，有4個集對的聯系數均為0.5，分別是集對H(A3，B)的聯系數、集對H(A15，B)的聯系數、集對H(A19，B)的聯系數和集對H(A33，B)的聯系數。根據最大聯系數判斷原則，預測值為集合A3、A15、A19和A33后續值的加權平均數，即2003年的預測年降雨量為1 114.2、1 243.5、1 186.5 mm和961.9 mm的加權平均數。經計算，2003年的預測降雨量為985.7 mm，而2003年的實際年降雨量為1 015.9 mm，預測誤差2.97%。同理可求得2004—2006年的預測年降水量。最后與量化處理方式預測結果進行比較，結果見表2。

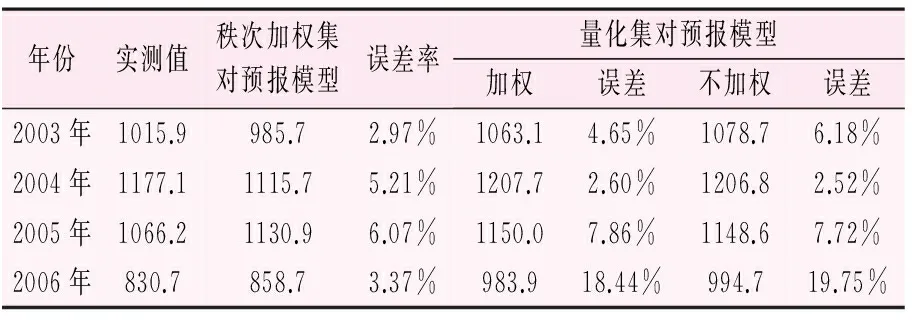
表2 秩次加權集對和量化集對預報模型預測值表 /mm

從表2可以看出，秩次加權集對預報模型和量化集對預報模型預測值最大誤差為19.75%(小于20%的預測合格標準)。大部分加權集對模型比不加權的預測值相對誤差小，大部分秩次加權集對預報模型預測值比量化集對預報模型預測值相對誤差小，且秩次加權集對預報模型的相對誤差均在10%以內，結果可靠度更高，可見集對分析在年降雨量預測方面可行有效。

4 結 語

集對分析預測方法簡單、便捷，在不對原始數據進行預處理的前提下，同時分析不確定因子間的同一性、差異性和對立性，從而能夠較好地描述不確定因子間的關系。本文構建了年降雨量秩次加權集對預報模型和量化加權集對預報模型，對都江堰雨量站年降雨量進行了預測，結果均滿足水文預報精度要求，可行有效；且秩次加權集對預報模型預報精度較其他集對預報模型相對誤差小，推薦采用秩次加權集對分析法對年降雨量進行預報。

參考文獻:

[1] SCHOLES R J, NOBLE I R. Storing Carbon on Land [J].Science, 2001, 29(02): 1012-1013.

[2] 歐源,張瓊,王文圣,等.基于秩次集對分析的年徑流預測模型[J].人民長江, 2009,40(03):63-65.

[3] 張銀迪,張小壯,張澤中.序位集對分析在遼河流域年降雨預測中的應用[J].安徽農業科學，2011，39(28):17534-17536.

[4] 許美玲.集對分析在云南強降水預報集成方法中的應用[J].氣象，2004，30(06)：39-42.

[5] 王紅芳,黃偉軍,王文圣.集對分析在長江寸灘站年徑流預測中的應用[J].黑龍江水專學報，2006，33(04)：3-5.

[6] 萬星,王文圣,丁晶.集對分析在水文水資源中的應用研究[J].水利水電科技進展，2006，26(04)：9-11.

[7] 馮利華,張行才,龔建林.關于集對分析的水文水資源變化趨勢的統計預測[J].水文，2004，24(02)：11-14.

[8] 王文圣,李躍清.水文水資源集對分析[J].南水北調與水利科技，2011，9(02)：27-32.

[9] 趙克勤.集對分析及其初步應用[M].杭州：浙江科學技術出版社，2000.

[10] 湯靜靜.集對分析在水文水資源分析評價和預測中的應用研究[D].成都：四川大學，2015.