川中丘陵區干旱多尺度長程相關性分析
詹 存,程 龍,盧錕明
(中國電建集團西北勘測設計研究院有限公司,西安 710065)
0 前 言
川中丘陵區是四川省重要的經濟作物產區,其農業發展對四川省的發展有著重要的意義。然而,川中丘陵區亦是四川省干旱頻發區,區內冬干春旱嚴重,干旱強度大、影響范圍廣、持續時間長,嚴重制約了四川省的社會經濟發展[1]。
干旱的強度和頻率通常用不同的干旱指標來描述,比如降水量距平百分率(Pa)、標準化降水指數(SPI)、Z指數、相對濕潤指數(M)、土壤相對濕度指數(R)、帕爾默干旱指數(PDSI)、綜合干旱指數(CI)等[2-5],標準化降水蒸散指數SPEI集合了SPI在多時間尺度、多地域上具有可比性的優點,同時考慮了溫度因素,使得其對全球氣候變暖下的干旱更加敏感[6]。熊光潔等已驗證了該方法在西南地區的適用性[7],因此,本文用標準化降水蒸散指數來分析川中丘陵區干旱特征。
傳統對極端氣候現象的研究,多假設所研究的時間序列中的各事件之間是相互獨立、完全隨機的,并且服從某一分布(如泊松分布)[8],在干旱的研究中,也多把干旱事件當作是獨立的事件來分析其頻率和強度。然而,各次干旱之間是緊密聯系的,即本次的干旱可能受之前干旱的影響,也可能對以后的干旱產生影響,對干旱的預測也是基于這一思想。因此,分析干旱事件之間的記憶性和持續性顯得尤為重要。
大多數研究表明,氣候系統具有自記憶性特征,氣候時間序列里存在著持續性[9-12]。以往對持續性研究的方法,如相關分析[13]、R/S分析法[14]、功率譜和小波分析[15]等,都是基于平穩的時間序列來進行分析的[16]。而類似干旱的氣候系統是比較復雜的,干旱的信號也多是非平穩的序列,以往分析序列持續性和相關性的方法在分析非平穩序列時存在缺陷。因此,為了分析干旱的長程相關性,有必要辨別由數據內在的長程波動引起的趨勢成分。
去趨勢波動分析法DFA(Detrended Fluctuation Analysis),被認為是檢驗時間序列長程相關性有效的工具[17]。DFA方法的優勢在于它消除了局部趨勢,能準確地觀察到時間序列本身所具有的統計行為特征,避免了將時間序列的短程相關、非平穩性虛假地檢測為長程相關性[18],自1994年Peng[19]等用以研究DNA序列的長程冪律相關性以來,被廣泛地用在醫學[20-21]、金融[22]、交通[23]、氣候學[24-25]等領域。
本文基于標準化降水蒸散指數,運用去趨勢波動分析法,分析了川中丘陵區多時間尺度干旱的長程相關性,并分析了該地區多尺度干旱的空間分布特征,以期為四川省的防旱減災提供科學參考。
1 研究區概況與數據處理
1.1 研究區概況
川中丘陵區是中國最典型的方山丘陵區,分布在四川盆地中部,海拔300.00~600.00 m[26]。西迄四川盆地內的龍泉山,東止華鎣山,北起大巴山麓,南抵長江以南,面積約8.4×104m2,地勢由西北向東南逐漸降低,南部多淺丘,北部多深丘,是一個典型的以農業為主導產業的地區[1]。川中丘陵區森林覆蓋率低,區內年降水量僅900~1 000 mm,冬干春旱明顯,棉花和甘蔗等主要糧經作物的產量低而不穩,嚴重制約了川中丘陵區農業的可持續發展[27]。
本文選取區內8個代表氣象站點,各站點的分布情況見圖1。

圖1 川中丘陵區氣象站點分布圖
1.2 數據處理
本文選取川中丘陵區內資料序列較長的8個國家基本氣象站1960—2012年的地面氣候資料月值數據(來自國家氣象數據共享服務網),包括月降水量、平均氣溫、平均風速、平均相對濕度、日照時數等。
序列的周期性波動會對長期相關的檢測產生顯著影響,容易導致檢測到并不存在的長期記憶[28]。氣象數據一般具有以年為周期的季節性波動,為了減輕季節性波動對長程相關性檢測的影響,本文采用滑動平均去季節性周期波動方法對氣象數據做平滑處理[29]。
2 研究方法
2.1 標準化降水蒸騰指數
本文采用的干旱指數是由Vicente-Serrano[30]提出的標準化降水蒸散指數SPEI,該指數是在SPI(Standardized Precipitation Index)指數的基礎上,通過引入潛在蒸散項構建的標準化降水蒸散指數SPEI以月平均降水和月平均氣溫為輸入,通過計算月降水與潛在蒸散的差值,并對差值做標準化處理,使其在不同地域間可以作比較,步驟如下[31]:
(1) 計算逐月降水量與潛在蒸散發的差值Di:
Di=Pi-PETi
(1)
式中:Pi為月降水量;PETi為逐月的潛在蒸散量,由Thornthwaite法計算。
(2)
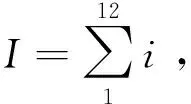
(2) 對差值D作標準化處理
在給定的時間尺度下,計算累積序列;對得到的累積序列采用廣義邏輯分布進行擬合,擬合方法采用線性矩法[32]。差值D的概率分布函數為:
(3)
式中:x為氣象數據樣本;α、β、γ分別為尺度、形狀及初始狀態參數,可由線性矩法(L-moment)估計獲得。C0、C1、C2和d1、d2、d3為概率分布函數轉化為累計頻率的簡化求解計算參數,取值如下:
C0=2.515517,C1=0.802853,
C2=0.010328,d1=1.432788,
d2=0.189269,d3=0.001308。
標準化降水指數計算公式如下:
(4)
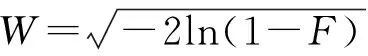

表1 SPEI指數干旱等級劃分表
2.2 去趨勢波動分析法
對于長度為N的原始序列{xk,k=1,2,…,N}去趨勢波動分析具體算法如下[33]。
(1) 建立一個新的序列
(5)
(2) 將新序列y(i)劃分為長度為s的不重疊等長度子區間,長度為N的序列共被分為Ns=INT(N/s)個子區間,因序列長度N不一定被s整除,為保證原序列信息不丟失,可以從序列末端開始反向再劃分一次,可以得到2Ns個子區間。
(3) 對每個子區間v(v=1,2,…,2Ns)的數據進行多項式回歸擬合,得到局部趨勢yv(i),yv(i)可以是一階、二階或更高階的多項式,記為DFA1、DFA2,計算方差均值:
i=1,2,…,Ns
(6)
i=Ns+1,Ns+2,…,2Ns
(7)
(4) 確定全序列的q階波動函數

(8)
(5) 通過分析雙對數坐標圖Fq(s)與s的關系,可以確定波動函數的標度指數α,即存在冪律關系:
Fq(s) ∝sα
(9)
可用最小二乘法線性擬合logFq(s)和logs,得到的斜率即為標度指數α。當α=0.5時,表明序列是隨機序列,無長程相關性;當0<α<0.5時,表明時間序列只具有短程相關性;當α>0.5時,表明序列各個值之間不是獨立的,具有長程相關性,當前發生的事件和未來的事件間存在著長程相關性;α越大,長程相關性越強,時間序列的可預測性越好。
3 結果與分析
3.1 川中丘陵區不同尺度干旱長程相關性
3.1.1 川中丘陵區長程相關性
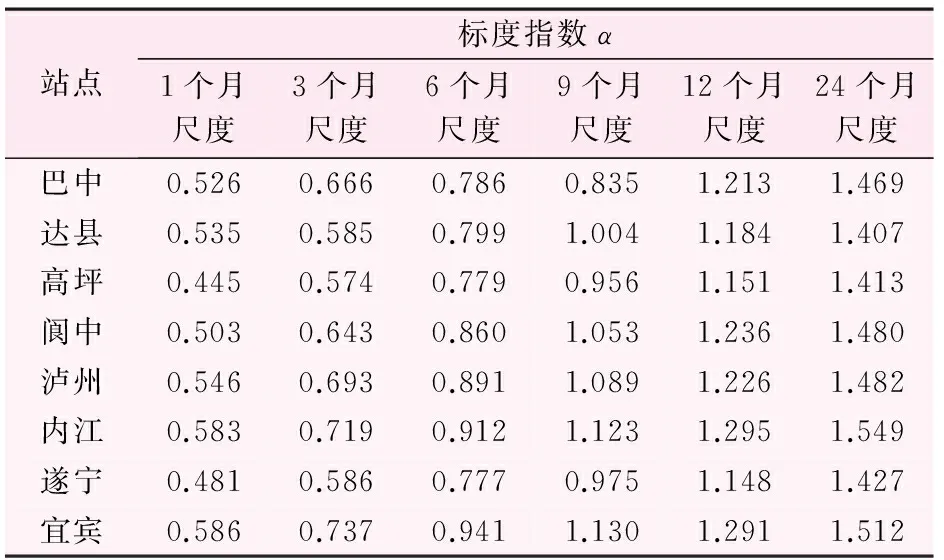
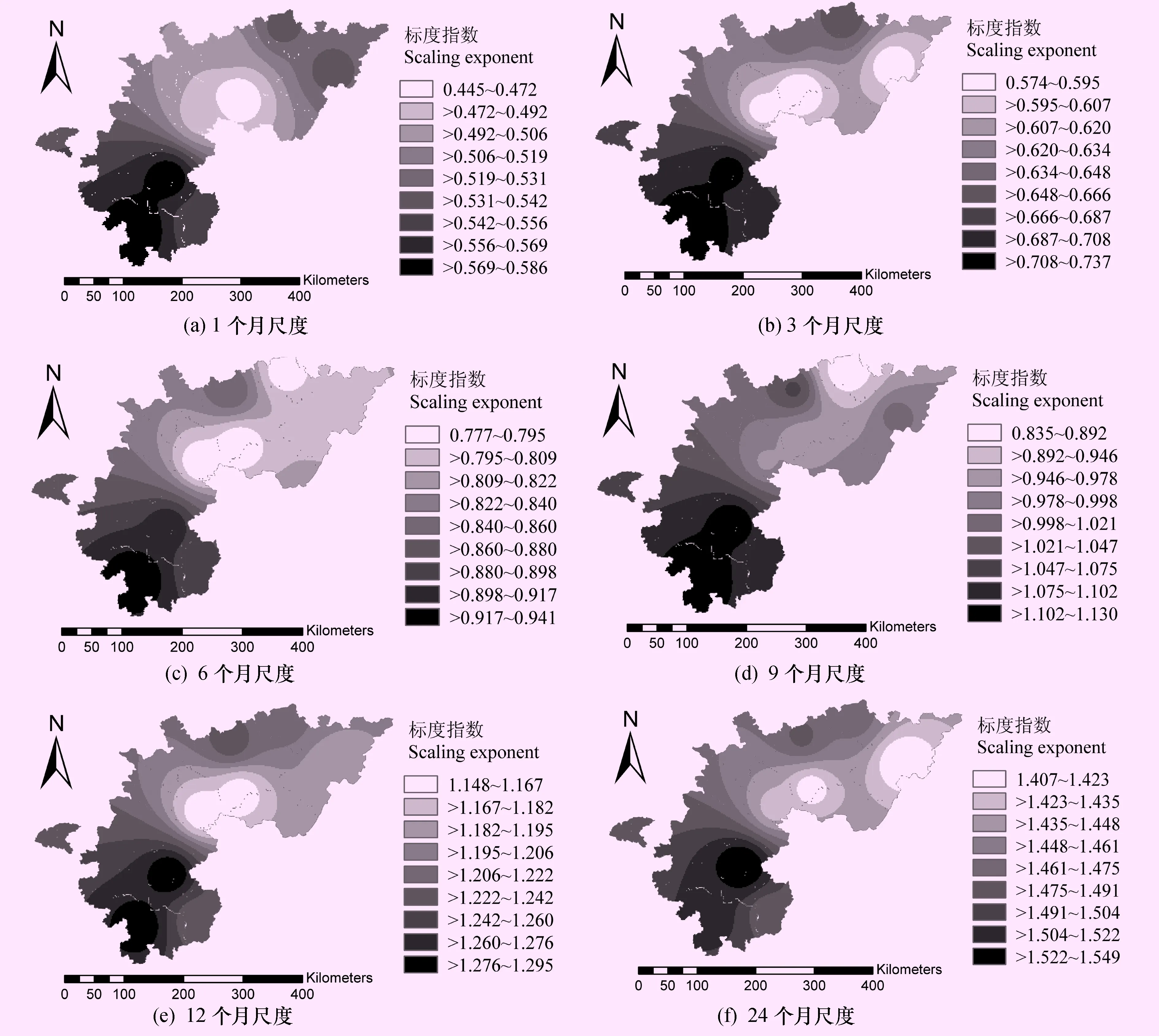
根據川中丘陵區8個國家氣象站點1960—2012年53 a的月氣象資料,資料序列長N=636,經過滑動平均去季節性周期波動方法濾去其季節性波動,標準化處理后,計算得到1、3、6、9、12個月和24個月的SPEI值。運用去趨勢波動分析法,對不同尺度的SPEI值進行分析。為了更好地估計標度指數α,一般定義分割區間q+2 對川中丘陵區不同時間尺度的標準化降水蒸散指數SPEI的波動函數Fq(s)和與分割區間s的對數值進行線性擬合,標度指數α即為logFq(s)和logs擬合直線的斜率。由圖2干旱序列的長程相關性可以看出,川中丘陵區1、3、6、9、12個月和24個月標準化降水蒸散指數的標度指數為0.526、0.652、0.844、1.062、1.288、1.366,不同尺度SPEI的標度指數均大于0.5,川中丘陵區不同時間尺度的SPEI值顯示出了長程相關性。 圖2 不同時間尺度干旱序列長程相關性圖 標度指數α的大小反映了長程相關性的強弱,標度指數越大,長程相關性越強。由圖2易知,川中丘陵區SPEI值標度指數范圍為0.526~1.366,標度指數隨著尺度的增大而增大,即長程相關性隨著時間尺度的增大而增強。究其原因,是因為氣候系統是一個復雜的系統,小尺度上,類似于干旱的氣候變化常具有突發性和不確定性,如2006年的川渝伏旱,2009年冬—2010春的西南干旱,而在大尺度上相對較穩定,這和王國杰[34]等的研究結果相一致。 3.1.2 不同站點多尺度長程相關性 以上從整個區域分析了整個川中丘陵區域干旱的長程相關性,為了更好地了解川中丘陵區干旱的標度指數特征,本文分析了川中丘陵區各站點不同時間尺度SPEI的標度指數,結果見表2。 由表2可以看出,不同站點SPEI值標度指數在不同時間尺度上表現出了差異性,除了高坪和遂寧在1個月尺度上的SPEI表現出短程相關性外,其它的時間尺度上各站點的SPEI值均大于0.5,標度指數范圍從0.445~1.549,表現出了長程相關性。從不同尺度來看,各站點SPEI值的標度指數總體上隨著時間尺度的增大而變大,長程相關性隨著尺度的變大而變強,干旱隨著時間尺度的增加變得更穩定,可預測性也越強,這和上一節的研究結論相似。 表2 川中丘陵區各站點標度指數分布表 為了討論川中丘陵區不同時間尺度干旱長程相關性的空間分布特征,此處首先計算統計年份內川中丘陵區各站點1、3、6、9、12個月和24個月尺度SPEI值,運用去趨勢波動分析法分析不同尺度SPEI值的標度指數,利用arcgis把各站點的標度指 數在空間上插值(見圖3),以標度指數的分布來反映川中丘陵區干旱長程相關性的空間分布特征。 由圖3可知,川中丘陵區各時間尺度的SPEI值的標度指數在空間上表現出差異性,總體而言,各尺度的標度指數在空間上總體表現為由川中丘陵區中部的達縣、高坪地區向川中丘陵區西南部和東北部遞增的現象,長程相關性也由川中丘陵區中部向東北和西南部逐漸加強。 從各尺度來看,1個月尺度上(圖3a),宜賓、瀘州、內江是標度指數的高值區,該區域的干旱指標表現出了較強的長程相關性,而中部的遂寧、高坪則是標度指數的低值區,該區域標度指數小于0.5,SPEI表現出短程相關性;3個月尺度(圖3b)和24個月尺度(圖3f)SPEI標度指數分布相似,內江、宜賓和瀘州區域的長程相關性最強,而高坪、遂寧和達縣干旱的長程相關性較弱;6個月尺度(圖3b)和12個月尺度(圖3f)SPEI標度指數分布相似,標度指數的高值區還是集中在川中丘陵區西南部的宜賓、內江附近,低值區集中在中部的遂寧、高坪附近,值得注意的是巴中,6個月尺度和12個月尺度的標度指數在空間上表現出相反的分布特征;9個月尺度(圖3d)的長程相關性高值區集中在宜賓、內江和瀘州附近,而低值區集中在巴中附近。 圖3 不同尺度干旱標度指數空間分布圖 總體而言,川中丘陵區西南部的宜賓、內江和瀘州地區的SPEI值的長程相關性較強,說明該地區不同尺度干旱具有長記憶性,干旱的特征較穩定,以往的干旱特征對以后干旱研究的參考價值高;遂寧、高坪和巴中地區干旱的長程相關性相對較弱,干旱的記憶性相對較弱,這增加了該區域干旱突發的可能性,是川中丘陵區防旱減災需要注意的區域,要加強在該區域干旱的預防和預警工作。 SPEI值的標度指數空間分布顯示(見圖3),川中丘陵區SPEI值的標度指數主要從西南向東北遞減,在經度方向和緯度方向上也表現出了明顯的分布特征,因此繪制了標度指數隨經緯度的分布圖,以探討該區域干旱長程相關性的空間結構特征,結果見圖4。 圖4 不同尺度干旱標度指數經緯向分布圖 圖4是川中丘陵區SPEI值標度指數的緯向和經向分布圖,標度指數幾乎都大于0.5。由圖4(a)標度指數的緯向分布可以看出,在28.5°N~29.0°N之間,川中丘陵區SPEI標度指數總體呈現減小趨勢,在29.6°N左右,標度指數突然增大,在30.5°N ~32.0°N之間,標度指數總體呈現增大的特點。由圖4(b)標度指數的經向分布可以看出,在104.6°E~107.5°E之間,川中丘陵區各尺度SPEI值的標度指數總體呈現隨經度增大而減小的趨勢。 干旱受到各氣象因子的綜合影響,各氣象因子對干旱的影響程度也不盡相同。以往的研究表明,川中丘陵區的干旱主要受到降水集中程度、平均風速、日照時數等因子的影響[1]。本文研究了不同時間尺度上的月平均降水量、月平均氣溫、日照時數、平均風速、平均相對濕度和標準化降水指數SPEI的標度指數(各氣象因子不同時間尺度的標度指數計算方法同SPEI值標度指數的計算,不同時間尺度氣象因子值用其對應的尺度的滑動平均值來表示),以探討這些氣象因子的標度指數與SPEI值標度指數的一致性,一致性越好,說明該氣象因子對川中丘陵區干旱長程相關性的貢獻越大,結果見表3。 表3 干旱指標標度指數與各氣象因子標度指數比較表 由表3可以看出,各尺度平均相對濕度與對應的標準化降水蒸散指數的標度指數一致性最好,說明平均相對濕度對川中丘陵區干旱長程相關性的影響是最大的,干旱的穩定性和長記憶性主要受平均相對濕度的影響,究其原因,是因為標準化降水蒸散指數是以降水量和溫度等為輸入的干旱指標,而平均相對濕度是這些氣象因子綜合作用的,因此平均相對濕度與標準化降水蒸散指數所描述的干旱在長程相關性上有一致性。平均風速和日照時數的標度指數也和SPEI的標度指數有一致性,這2個氣象因子是使得川中丘陵區干旱具有長程相關性的又一因素,對川中丘陵區干旱也起著重要的作用,這在一定程度上驗證了詹存[1]等的研究。相較而言,平均降水量、平均溫度的標度指數和SPEI值標度指數的一致性稍差,這主要是因為平均降水量和平均溫度只是SPEI值計算的一個輸入,對SPEI值的影響相對有限。 綜上所述,平均相對濕度是影響川中丘陵區干旱長程相關性的主要因素,其次是平均風速和日照時數。這可以為該區域干旱的預測和評價工作提供參考。 根據川中丘陵區1960—2012年的月氣象資料,基于標準化降水蒸散指數SPEI,計算了該區域1、3、6、9、12個月和24個月的SPEI值,并運用去趨勢波動分析法研究了不同尺度SPEI值標度指數的時空分布特征,得到如下結論: (1) 川中丘陵區不同時間尺度的標準化降水蒸散指數均表現出了長程相關性,并且長程相關性隨著時間尺度的增加而增強。 (2) 川中丘陵區SPEI標度指數在空間上總體從西南向東北遞減,宜賓、瀘州、內江是標度指數的高值區,而高坪、遂寧和巴中則是低值區。 (3) 川中丘陵區SPEI標度指數在空間機構上表現出差異性,在經向分布上,標度指數總體呈現減小的趨勢。 (4) 在影響川中丘陵區干旱的眾多氣象因子中,平均相對濕度的標度指數和SPEI值的標度指數表現出較好的一致性,平均相對濕度對該區域干旱的長程相關性作出重要貢獻。 去趨勢波動分析法是檢測干旱等時間序列長程相關性的有效的工具,被廣泛地運用在氣候系統的長程相關性檢測中。干旱氣候系統是復雜的系統,常受地形地貌、大氣環流、氣象因子等綜合影響,具有形成原因復雜、影響因素多、突發性強、影響范圍廣、可預測性差等特點,因此,研究干旱的長程相關性特征對干旱的預測和預警有著重要的意義。全球氣候變暖,可能導致川中丘陵區干旱的長程相關性出現新的變化,因此,考慮氣候變暖的全球氣候模式和區域性降尺度方法與去趨勢波動方法結合來分析川中丘陵區干旱的記憶性和分形特征,值得進一步來研究。 參考文獻: [1] 詹存,梁川,趙璐.川中丘陵區季節性干旱時空分布特征及成因分析[J]. 農業工程學報,2013,29(21):82-90. [2] 黃晚華,楊曉光,李茂松,等.基于標準化降水指數的中國南方季節性干旱近58a演變特征[J].農業工程學報,2010,26(07):50-59. [3] 王明田,王翔,黃晚華,等.基于相對濕潤指數的西南地區季節性干旱時空分布特征[J]. 農業工程學報,2012,28(19):85-92. [4] 張寶慶,吳普特,趙西寧,等.基于可變下滲容量模型和Palmer干旱指數的區域干旱化評價研究[J].水利學報,2012,43(08):926-934. [5] 包云軒,孟翠麗,申雙河,等.基于CI指數的江蘇省近50年干旱的時空分布規律[J].地理學報,2011,66(05):599-608. [6] 楊偉光,易雪,侯美婷,等.基于標準化降水蒸散指數的中國干旱趨勢研究[J].中國生態農業學報,2012,20(05):643-649. [7] 熊光潔,張博凱,李崇銀,等.基于SPEI的中國西南地區1961-2012年干旱變化特征分析[J].氣候變化研究進展,2013,9(03):192-198. [8] 封國林,王啟光,侯威,等.氣候領域極端事件的長程相關性[J].物理學報,2009,58(04):2853-2860. [9] 劉式達,袁乃明,付遵濤.氣候變化的長期記憶性:理論基礎與觀測證實[J].中國科學:物理學 力學 天文學,2013,43(10):1327-1331. [10] 江志紅,常奮華,丁裕國.基于馬爾科夫鏈轉移概率極限分布的降水過程持續性研究[J].氣象學報,2013,71(02):286-294. [11] 杜海波,吳正方,張娜,等.近60 a丹東極端溫度和降水事件變化特征[J].地理科學,2013,33(04):473-480. [12] 郜建華,薛惠文.對云量的長程相關性研究[J].北京大學學報(自然科學版),2011, 47(04):613-618. [13] 趙玉萍,張憲洲,王景升,等.1982年至2003年藏北高原草地生態系統NDVI與氣候因子的相關分析[J].資源科學,2009,31(11):1988-1998. [14] 張鑫,蔡煥杰,尹曉楠.應用重標度極差分析法(R/S)分析無定河流域水沙變化[J].農業工程學報,2010,26(Z2):212-217. [15] 謝五三,田紅.安徽省近50年干旱時空特征分[J].災害學,2011,26(01):94-98. [16] 趙靜,呂繼強,寧有豐,等.西安市降雨和氣溫的非趨勢性波動分析[J].水資源與水工程學報,2011,22(02):74-76. [17] 侯威,章大全,楊萍,等.去趨勢波動分析方法中不重疊等長度子區間長度的確定[J].物理學報,2010,59(12):8986-8993. [18] 王啟光,侯威,鄭志海,等.東亞區域大氣長程相關性[J].物理學報,2009,58(09):6640-6650. [19] Peng C K, Buldyrev S V, Havlin S, et al. Mosaic organization of DNA nucleotides[J].Physical Review E, 1994, 49(02): 1685-1689. [20] 成克強,王俊.早搏心電信號的標度不變性分析[J].生物醫學工程學雜志,2010,27(04):753-756. [21] 江麗儀,吳效明.睡眠時相與心率變異性的關系研究[J].生物醫學工程學雜志,2011,28(01):148-152. [22] 苑瑩,杜樂鹿,莊新田.股市收益率與交易量長記憶性實證研究[J].東北大學學報(自然科學版),2012,33(07):1056-1059. [23] 吳建軍,徐尚義,孫會君.混合交通流時間序列的去趨勢波動分析[J].物理學報,2011,60(01):1-7. [24] 趙靜,呂繼強,寧有豐,等.西安市降雨和氣溫的非趨勢性波動分析[J].水資源與水工程學報,2011,22(02):74-76. [25] 黃淑紅,呂繼強,沈冰,等.基于去趨勢波動分析的降雨演變特性研究[J].西安理工大學學報,2010,26(02):148-151. [26] 趙璐,梁川,崔寧博,等.不同ET0計算方法在川中丘陵區的比較及改進[J].農業工程學報,2012,28(24):92-97. [27] 徐精文,楊文鈺,任萬君,等.川中丘陵區主要農業氣象災害及其防御措施[J].中國農業氣象,2002,23(03):49-52. [28] 宋閏柳,于靜潔,劉昌明. 基于去趨勢波動分析方法的土壤水分長程相關性研究[J].水利學報,2011,42(03):315-322. [29] 李玉河.具有季節特征的水文時間序列預測模型研究[J].灌溉排水學報,2007,26(06):93-95. [30] Vieente-Serrano S M, Begueria S, LoPez-Moreno J I. A multiscalar drought index sensitive to global warming: the standardized Precipitation evapotranspiration index[J].Journal of Climate, 2010, 23(7):1696-1718. [31] 陳子燊,黃強,劉曾美.1962 - 2007年廣東干濕時空變化特征分析[J].水科學進展,2013,24(04):469-476. [32] Hosking J R M. L-moments: Analysis and estimation of distributions using linear combinations of order statistics[J].Journal of the Royal Statistical Society: Series B (Methodological), 1990:105-124. [33] 封國林,侯威,支蓉,等.極端氣候事件的檢測、診斷與可預測性研究[M].北京: 科學出版社,2009:33-35. [34] 王國杰,姜彤,陳桂亞.長江干流徑流的時序結構與長期記憶性[J].地理學報,2006,61(01):47-56.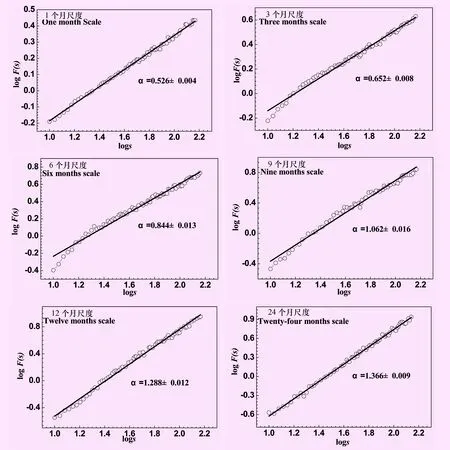
3.2 干旱長程相關性空間分布
3.3 干旱長程相關性分布的空間結構特征

3.4 不同尺度干旱與各氣象因子的長程相關性

4 結 語

