芻議向量在新視域下高考數(shù)學(xué)中的“活躍性”探究

楊 寧

(河南師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，河南 新鄉(xiāng) 453007)

一、前言

鑒于向量同時(shí)兼?zhèn)鋷缀涡问胶痛鷶?shù)形式這一特點(diǎn)，在和其他知識(shí)點(diǎn)交匯處命制高考題順其自然就備受高考命題者所青睞。作為串聯(lián)多個(gè)知識(shí)點(diǎn)交匯的媒介，在填空題和選擇題方面其綜合能力較強(qiáng)；在數(shù)學(xué)思想方面，重點(diǎn)設(shè)計(jì)到化歸思想，數(shù)形結(jié)合思想以及分類討論等數(shù)學(xué)思想。常見的主要有三角函數(shù)與向量的綜合命題，函數(shù)與向量，不等式與向量以及壓軸題圓錐曲線和向量的綜合命題等等，最終都是以求代數(shù)問題而告終。而對(duì)于學(xué)生來說，主要考查學(xué)生的邏輯推理能力和運(yùn)算能力等。同時(shí)也考查學(xué)生是否能綜合巧妙的運(yùn)用這些知識(shí)點(diǎn)去解決交匯問題的能力。本文例說高考數(shù)學(xué)中向量與其它知識(shí)的交匯及相關(guān)的解題策略。

二、向量與其他知識(shí)的交匯與融合

縱觀近幾年的考試，在向量的命題方面，單獨(dú)命題的試題量甚微，但凡涉及到向量的試題都有一個(gè)明顯的特點(diǎn)——加大了對(duì)交匯題的考查，充分體現(xiàn)了考試說明中“在知識(shí)交匯處”命題的一個(gè)基本原則。

(一)平面向量與平面幾何的交匯

例 已知ΔABC中，∠C是直角，CA=CB，D是CB的中點(diǎn)，E是AB上一點(diǎn)，且AE=2EB，求證：AD⊥CE.

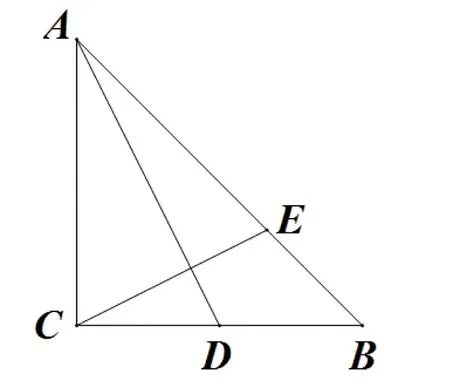
證明：建立如圖所示的直角坐標(biāo)系，設(shè)E(x,y)、A(0,a),則B(a,0).

(二)平面向量與解析幾何中的交匯

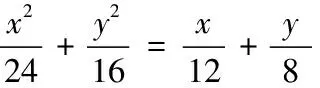
(三)平面向量與三角函數(shù)、函數(shù)等知識(shí)的結(jié)合

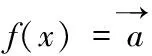
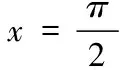
(四)平面向量與不等式的交匯

例 已知實(shí)數(shù)a、b、c滿足a+b+c=0，且a2+b2+c2=1，求a的最大值.

(五)向量與方程的交匯

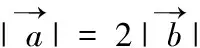
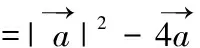
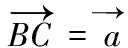
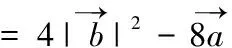
(六)向量與立體幾何的交匯

(1)求證：DM⊥平面ABC；

(2)求二面角C-BM-D的大小.

證明：如圖，取BD中點(diǎn)N，連結(jié)AN,CN∵將邊長(zhǎng)為2的正方形ABCD沿對(duì)角線BD折疊，使得平面ABD⊥平面CBD，∴AN⊥BD，CN⊥BD，

∵平面ABD⊥平面CBD，平面ABD∩平面CBD=BD，CN?平面CBD，CN⊥BD，∴CN⊥平面ABD。

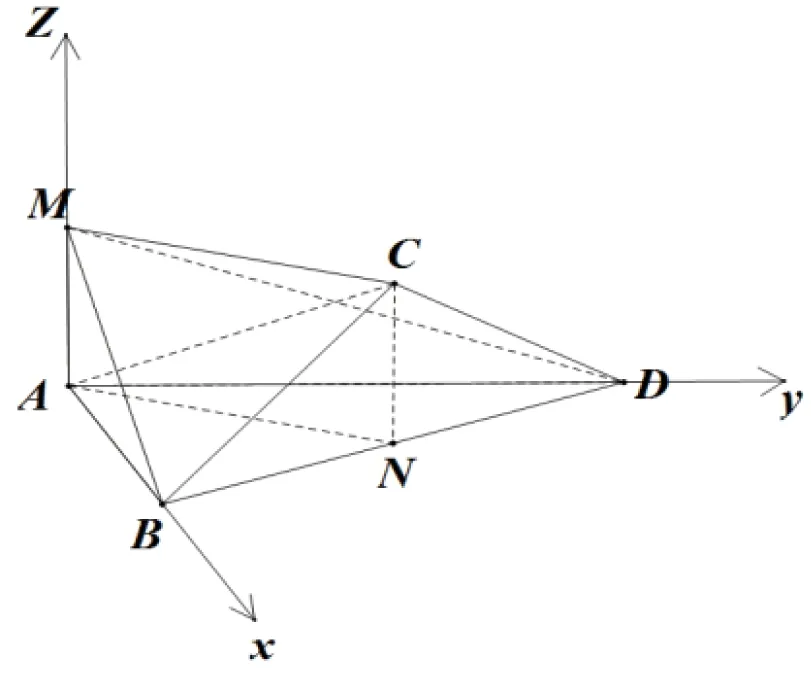
以A為原點(diǎn)，AB、AD、AM所在直線分別為x軸，y軸，z軸，建立空間直角坐標(biāo)系：則

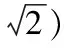
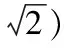
三、結(jié)語(yǔ)

新視域下，新課程增加了現(xiàn)代數(shù)學(xué)內(nèi)容——向量。其目的不僅在于高中數(shù)學(xué)內(nèi)容方面上的更新，更重要的是將新的思維方法帶入了高中數(shù)學(xué)中來，因此可以更有效地處理和解決數(shù)學(xué)問題以及實(shí)際應(yīng)用問題，也從中啟示我們?cè)诟咧袑W(xué)習(xí)數(shù)學(xué)時(shí)，應(yīng)著重突出向量的工具性，注重向量與其它知識(shí)的交匯與融合，切忌諱深層次挖掘。

通過以上的例說，不難看出，借用向量知識(shí)，降低了很多題型的運(yùn)算難度，同時(shí)也減小了運(yùn)算量，向量知識(shí)在高中數(shù)學(xué)中作為一個(gè)新的知識(shí)，在學(xué)習(xí)數(shù)學(xué)中起到了至關(guān)重要的作用，在多個(gè)知識(shí)點(diǎn)交匯的地方完美的體現(xiàn)出了數(shù)與形的統(tǒng)一。我們?cè)谘芯繑?shù)學(xué)問題時(shí)，借助向量這個(gè)獨(dú)特的工具，使我們能深刻的透過數(shù)學(xué)現(xiàn)象看出其中的本質(zhì)問題，從而使問題得到相應(yīng)的解決。

此外，在高考命題方面，命題專家會(huì)根據(jù)知識(shí)點(diǎn)交匯為突破口命題。作為教師，在高中數(shù)學(xué)中，常把其它問題進(jìn)行化歸，變成為簡(jiǎn)單的向量計(jì)算，其中將抽象的邏輯推理演變?yōu)榫唧w的向量運(yùn)算，實(shí)現(xiàn)了數(shù)與形的完美結(jié)合，所以平面向量為載體的數(shù)學(xué)試題與其它數(shù)學(xué)知識(shí)聯(lián)系緊密，具有很強(qiáng)的時(shí)代氣息，因此倍受命題老師的青睞。因此要正確引導(dǎo)學(xué)生把握常見題型的特點(diǎn)，讓學(xué)生多次的反復(fù)熟悉其蘊(yùn)含的數(shù)學(xué)思想以及解題方法，在考場(chǎng)上能應(yīng)對(duì)自如，同時(shí)要注意符號(hào)的書寫，抓住重點(diǎn)內(nèi)容，輕松應(yīng)考。

參考文獻(xiàn)：

[1]呂世虎.高中數(shù)學(xué)新課程中的向量及其教學(xué)[J].課程·教材·教法，2006(1).

[2]金小欣.向量與其他數(shù)學(xué)知識(shí)的交匯[J].數(shù)學(xué)大世界·高中版，2005(4).

[3]李鋒.平面向量與其他知識(shí)的交匯賞析[J].數(shù)理化學(xué)習(xí)(高中版)，2011(12).