放飛過程中平流層飛艇運動與受力分析

張泰華， 姜魯華， 周江華

(1. 中國科學院光電研究院， 北京 100094； 2. 中國科學院大學， 北京 100049； 3. 中國科學院高能物理研究所， 北京 100049)

由于平流層在大氣環境、氣象條件和高度等多方面的綜合特點，在平流層部署飛艇進行長期環境監測、通信中繼和對地觀測成為研究熱點[1]。平流層飛艇的工作高度比衛星低，電波傳播時延小，自由空間損耗小，造價相對較低。同時，平流層飛艇還有較強的抗毀生存能力。因此，平流層飛艇效費比將高于其他亞軌道飛行器和低軌衛星，在區域監控和天-地、天-空信息交互方面優勢明顯，無論是在軍用，還是科學及民用領域，都具有極其廣闊的應用前景[2-3]。在國際上，美國和日本等國進行了一些探索性試驗，美國HiSentinel系列[4-5]和HALE-D[6-7]飛艇曾進行了一些關鍵技術探索和飛行試驗，日本GTS系列[8]和SPF[9]不帶動力飛艇也曾在升空試驗中成功到達了平流層高度，這些工作為平流層飛艇技術的發展積累了一定的經驗。

從解除地面設備對飛艇的約束到飛艇離開地面的過程即為飛艇的放飛過程。將體積龐大的平流層飛艇從艇庫轉運至放飛場，并盡快實施放飛決定了整個飛行試驗是否能順利實施，一些平流層飛艇在放飛階段即被迫推遲或取消飛行試驗[6-7,9]。平流層飛艇放飛后，由靜止開始加速上升，艇體內氦氣竄動引起浮心和重心變化導致飛艇運動復雜，龐大的體積和巨大的表面積導致了氣動與附加質量的疊加，影響了飛艇的動力響應。位于柔性艇體上設備在放飛過程中的過載及其對柔性艇體的應力集中進一步增加了放飛過程的不確定因素和風險。

隨著飛行試驗的開展，國內外對平流層飛艇放飛過程也進行了大量研究。Selby[10]對平流層飛艇在不同工況下放飛及放飛后的特性做了較為深入的研究，分別分析了在順風和逆風情況下實施放飛時所受的氣動力及放飛風險；趙攀峰等[11]以常規布局形式的平流層飛艇為例，分析了飛艇放飛、回收的一般步驟，對上升、下降過程做了數值仿真分析；郭虓等[12]分析了飛艇基本熱力學行為，研究了艇體及內部氣體的能量方程并建立了詳細的飛艇動力學和運動學模型，通過對不同場景的問題進行最優化軌跡求解，評估了飛艇在上升過程中，太陽能輻射和風場對熱交換的影響，進而將不同時間點放飛對飛艇的影響進行了評估；吳雷等[13]分析了飛艇在放飛過程中因其所處環境的巨大變化導致飛艇內部氣體質量和分布情況的變化情況，給出了能基本反映這一變化過程的飛艇放飛段動力學模型。總的來說，這些研究主要對飛艇放飛時機的選擇及模型的求解進行了定性的分析，還沒有開展較為系統的研究。

本文分析了放飛過程飛艇動力學響應特征，計算飛艇完成放飛所需的時間，以及在此期間飛艇的仰角、角速度和地面支撐力等變化。將計算結果與飛行試驗比較，為平流層飛艇放飛過程提供了解析求解方法，也為相關操作及地面輔助措施的選擇提供參考。本文在計算過程中忽略地面風對放飛過程的影響，主要分析放飛過程中的艇體氣動阻力。

1 平流層飛艇囊體結構形式

平流層飛艇通常選擇在20 km左右的平流層底部飛行或駐留，平流層大氣稀薄，要依靠浮力保持穩定駐空，需要飛艇具有較大的體積，一般在數萬至數十萬立方米之間，飛艇的長度在百米量級[14]。平流層飛艇在地面時，由于大氣密度較高，只需在飛艇內充入較少的氦氣就能提供滿足所需的升空浮力，艇囊90%以上的空間中充滿空氣以使飛艇保持設計外形。一般而言，平流層飛艇的艇囊可分為單氦氣囊和多氦氣囊2種形式，如圖1所示。

單氦氣囊結構中，艇囊中的氦氣都在一個氦氣囊中，與空氣囊之間只有一個副氣囊隔層，在飛艇縱向一般對氣體無約束。日本于2003年8月成功實施了飛行試驗的SPF-1飛艇即采用了單氦氣囊結構[9]，飛艇前點解除約束后，飛艇加速抬頭升空，放飛照片如圖2所示。

多氦氣囊結構中，艇囊中的氦氣和(或)空氣被分割成了2個以上的單獨空間，以限制其在飛艇縱向的竄動，防止飛艇姿態變化超出可控范圍。為了便于在飛艇上升過程中排氣順暢和保持壓差穩定，也可將氦氣囊或空氣囊進行局部聯通。

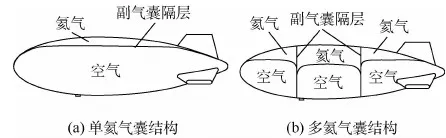
圖1 平流層飛艇氦氣囊結構示意圖Fig.1 Schematic of helium-envelope structure of stratospheric airship

美國于2011年7月進行了“HALE-D”平流層飛艇飛行試驗[6-7](見圖3)，該飛艇解除兩側約束后，飛艇姿態平穩，推測其囊體結構采用了多氦氣囊結構形式。

本文對平流層飛艇采用2種氦氣囊結構形式的放飛過程進行分析，并將分析得到的單氦氣囊結構的定量結果與飛行試驗過程中獲得的數據進行對比，驗證分析計算方法的正確性，也為進一步優化放飛過程的操作提供依據。

圖2 SPF-1飛艇放飛(日本)Fig.2 Launch of SPF-1 airship (Japan)

圖3 HALE-D飛艇放飛(美國)Fig.3 Launch of HALE-D airship (USA)

2 單氦氣囊結構放飛過程分析

根據單氦氣囊結構的特點和安全可靠放飛的要求，一種典型的平流層飛艇放飛過程如圖4所示。放飛前，飛艇接近于水平放置，艇體兩側各用2根繩索拉住，并使艇體后部坐落在支撐墊上，艇體處于小仰角狀態；放飛時，解除艇體兩端約束，在浮力作用下，艇體快速抬頭，仰角迅速增大，當艇體前部升到一定高度時，后部脫離支撐墊，飛艇以大仰角狀態起飛離地，放飛過程完成。

圖4 一種單氦氣囊結構飛艇的放飛過程Fig.4 Launch process of airship with single helium envelope structure

2.1 飛艇受力

飛艇依靠內部充氣達到一定的正壓，以保證其設計外形并使其具有一定的剛度。據此，假設飛艇為剛體，建立如圖5所示坐標系。OXY坐標系為地面坐標系，O′xy為艇基坐標系，以飛艇體心為坐標原點，O′x軸為飛艇縱軸，O′z軸垂直O′xy平面，坐標軸符合右手法則。

圖5中：T1和T2分別表示地面設備對飛艇約束力；Fb為艇囊內氦氣總浮力；Nx、Ny為飛艇所受的接觸力；G為艇體結構重力。

為使問題具有普遍性，假設飛艇在放飛前初始仰角為φ0。從后往前依次解除兩端拉繩T2、T1的約束，飛艇前部逐漸升起。在此過程中的某一時刻，飛艇受力和角度如圖6所示。

圖5 飛艇放飛前受力示意圖Fig.5 Force diagram before airship launch

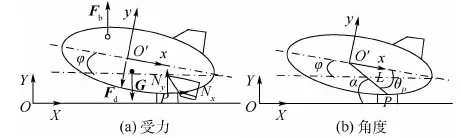
圖6 飛艇放飛過程中受力與角度示意圖Fig.6 Schematic of force status and angle during airship launch process

地面坐標系與艇體坐標系的關系為

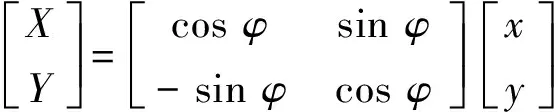
(1)

2.2 動力學方程

飛艇放飛前系統靜止，力系平衡，有

(2)

式中：Fb、Fd和N分別為浮力、氣動阻力和腹部支撐力。放飛后，在體心坐標系上建立方程，可得矢量形式的動力學方程[15]為

(3)

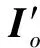
展開后，可得到6自由度標量形式的動力學方程。本文著重考慮飛艇發放過程縱剖面內的運動，因此抽取其縱向3自由度標量形式的動力學方程如下：

(4)

式中：MN為飛艇所受的接觸力矩；Fx、Fy和Mz分別為浮力、重力、氣動阻力產生的合力分量和合力矩；(xa,ya)為飛艇系統總質心。

式(4)變換后得

(5)

式中：J為飛艇轉動慣量。

(6)

其中：mAx、mAy和Iz、IAz分別為附加質量和慣性矩。

運動學方程：

(7)

式中：φ為飛艇仰角。

(8)

2.3 約束條件

在放飛過程中，假設飛艇與支撐點P之間無相對滑動，飛艇質心與支撐點P之間距離為L。當飛艇仰角為φ時，圖6中各角度間關系為

α=φ+θP

(9)

將飛艇姿態變化過程中質心近似為不變，則θP為常數，對式(9)求導，有

(10)

(11)

對式(11)求導，可得

(12)

將式(11)、式(12)代入式(5)，得

(13)

2.4 力和力矩

根據飛艇受力，將飛艇受到的氣動阻力分解為沿x和y2個方向，根據飛艇外形仿真得到這2個方向氣動阻力系數[16]，有

MN=L(NycosθP-NxsinθP)

(14)

(15)

式中：(xb,yb)為飛艇浮心；Ff為凈浮力；Fdx和Fdy為飛艇氣動阻力。

根據飛艇氣動阻力公式[17]，將式(11)代入得

(16)

由式(13)～式(16)得到解除約束后的動力學微分方程

(17)

式中：

f1=-L2(mycos2θP+mxsin2θP)+

2mL(xacosθP+yasinθP)-Jz

(18)

f2=L2[(mx-my)cosθpsinθp+

(19)

f3=Fb(xbcosφ+ybsinφ)-FfL(cosφcosθP+

sinφsinθP)-mg(xacosφ+yasinφ)

(20)

式(17)與式(7)、式(8)一起構成了方程的解。支撐點P所受的約束力，可由式(13)和式(15)得到，轉換到地面坐標系為

NX=Nxcosφ+Nysinφ

(21)

NY=-Nxsinφ+Nycosφ

(22)

2.5 輔助方程

飛艇系統總質量為

m=ms+mHe+mair=

(23)

式中：c=ρ/ρHe，ρHe為氦氣密度；ms、mHe和mair分別為艇體結構、氦氣和空氣的質量。系統總質心為

(24)

式中：(xs,ys)為艇體結構質心。總慣量為

(25)

式中：IHe、Iair和Is分別為氦氣、空氣和艇體的結構慣量；Izt為艇體幾何慣量；Izb為氦氣部分幾何慣量。附加質量[18]和慣性矩為

(26)

式中：k1、k2和k3為附加質量系數。

2.6 工況分析

1) 飛艇放飛瞬間

在飛艇解除約束瞬間，由于ωz=0，由式(17)可求得此時飛艇初始角加速度：

(27)

根據艇上設備位置，進而可得艇上設備放飛時受到的初始過載。

2) 飛艇離地

因支撐點P無法提供拉力，由式(22)可得，當NY<0時，飛艇離開支撐點P，完成放飛。

3 多氦氣囊結構放飛過程分析

多氦氣囊結構中，艇囊內設置多個氦氣囊，極大地限制了因飛艇姿態變化而導致的氦氣竄動，也嚴格控制飛艇浮心變化。在飛艇放飛升空過程中，飛艇姿態一直處于可控狀態。實施放飛時，飛艇一般小仰角或水平狀態離地，其飛行過程如圖7所示。

在實施這種結構飛艇的放飛過程中，飛艇浮心與重心保持不變，飛艇的運動形式將大大簡化，解除約束后，飛艇加速上升。飛艇在放飛前后的約束及受力狀態如圖8所示。

圖7 多氦氣囊結構飛艇的飛行過程Fig.7 Flight process of airship with multi-helium envelope structure

圖8 多氦氣囊結構飛艇放飛前后受力Fig.8 Force status for multi-helium envelope structure before and after airship launch

解除約束后，在不考慮水平來流的情況下，飛艇將垂直上升，即

(28)

根據飛艇動力學方程，由式(4)變換后得

(29)

將式(29)中第1式代入第2式，整理得

(30)

在上升過程中的氣動阻力，由式(16)有

從當今互聯網發展的現狀來看，強調用戶量、用戶關系、優質的內容依然是互聯網發展中的有效保證。移動互聯網的發展帶來了哪些影響呢？改變了內容生產的分發方式，慢慢實現了中心化。在生產內容上，人人都可以成為內容的提供者，使移動互聯網進入了全民時代。也是因為如此，移動短視頻的生產內容逐步走向多元化。其中，最具有代表的兩種：UGC和PGC。

(31)

代入式(15)，得

(32)

式中：g為重力加速度。

將式(32)代入式(30)，得

(xbcosφ+ybsinφ)Fb-(xacosφ+

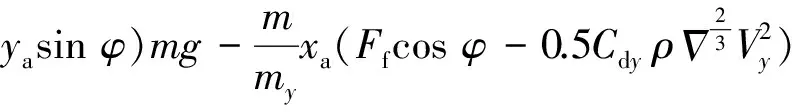
(33)

式(33)與式(7)、式(8)一起構成了方程的解。

(34)

代入式(32)，得

(35)

由式(35)即可求得穩定上升時的升速，也可根據設計升速，求出飛艇所需凈浮力。

4 算 例

4.1 單氦氣囊結構

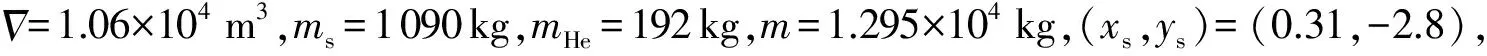
根據上述分析，得到支撐點P受到的作用力(NX,NY)隨時間變化曲線如圖10所示。

飛艇在放飛過程中，質心水平和垂直速度的變化如圖11所示，飛艇仰角隨時間變化的計算結果和實測數據對比如圖12所示，角速度隨時間變化的計算結果和實測數據的對比如圖13所示。從圖12和圖13的對比曲線可以看出，飛艇實際放飛中解除約束的響應比計算分析結果明顯遲滯，這主要是因為在分析中將飛艇是近似為剛體，而實測角速度值較為發散是飛艇上的角度傳感器的測量誤差所致，但在變化趨勢與計算結果一致，能夠滿足工程應用需求。

通過上述分析計算，得到飛艇整個放飛過程中的姿態變化如圖14所示。

計算表明，飛艇放飛后17.9 s，NY<0，此后飛艇離開支撐點，也意味著飛艇完成放飛離開地面，此時飛艇仰角為43.8°。在飛艇放飛過程中，支撐點水平作用力最大NXmax=6.183 kN，支撐點垂直作用力最大NYmax=2.405 kN。

圖9 參數xb,yb和Izb隨飛艇仰角變化示意圖Fig.9 Fluctuation of parameter xb,yb and Izb with airship elevation angle

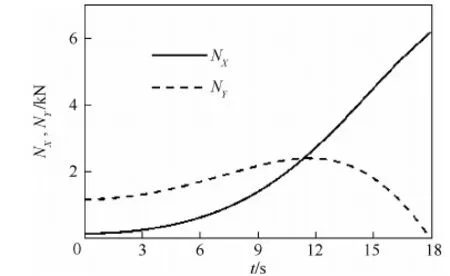
圖10 飛艇放飛過程NX,NY變化Fig.10 Fluctuation of NX,NY during airship launch process

圖11 飛艇放飛過程中質心速度變化Fig.11 Fluctuation of center-of-mass velocity during airship launch process

圖12 飛艇仰角計算結果與實測數據對比Fig.12 Comparison of elevation angle of airship between calculation results and flight test data

圖13 飛艇角速度計算結果與實測數據對比Fig.13 Comparison of angular velocity of airship between calculation results and flight test data

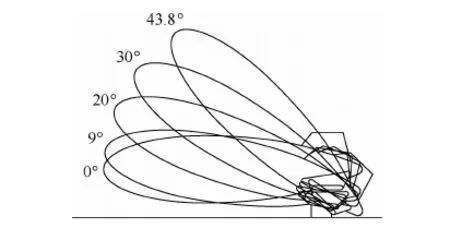
圖14 飛艇放飛過程中的姿態變化Fig.14 Change of airship attitude during launch process

4.2 多氦氣囊結構

如果算例所示飛艇采用多氦氣囊結構形式，解除約束后飛艇重心和浮心都保持不變，利用第3節分析，可以得到飛艇解除約束后的仰角和升速變化如圖15所示。

由圖15可知，如果算例中的飛艇采用多氦氣囊結構，放飛后穩定升速為1.56 m/s。在放飛過程中，解除約束后，飛艇升速在3～5 min內趨于穩定，仰角在21°～5°之間進行寬幅波動后趨于穩定。增大浮重比對飛艇仰角影響較小，但能顯著增大穩定升速。如果平流層飛艇要快速升空，并安全穿過對流層頂疾風區，需增大浮力，以增大飛艇穩定升速。為此，以浮重比η作為輸入參數，其定義為

(36)

不同的浮重比，飛艇穩定升空時的仰角和升速如表1所示。

由表1計算結果可知，飛艇浮重比增大，飛艇穩定升速增大，但對飛艇穩定仰角影響較小。選取浮重比η分別為1.1、1.5和1.8三種情況下，飛艇放飛后的升速變化如圖16所示。

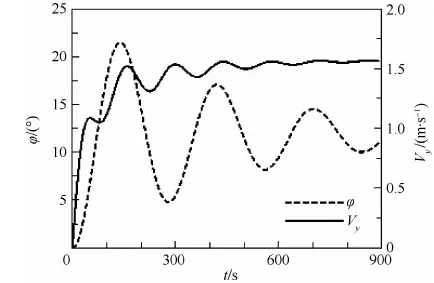
圖15 放飛后飛艇仰角與升速變化Fig.15 Fluctuation of pitch angle and rising velocity of airship after launch

浮重比仰角/(°)升速/(m·s-1)1．111．131．561．211．412．201．311．562．691．411．663．111．511．723．471．611．773．811．711．814．111．811．844．391．911．864．662．011．884．91

圖16 3種典型浮重比下飛艇升速變化Fig.16 Fluctuation of rising velocity of airship for three typical buoyancy-weight ratios

4.3 兩種結構形式比較

通過上述分析可知，氦氣囊結構設計對飛艇放飛和升空影響很大，不同的氦氣囊結構形式決定了飛艇放飛方式。在飛艇升空過程中，升速是一個非常重要的技術指標，以算例中的飛艇為例，不同的設計升速與所需的浮重比η如圖17所示。

采用單氦氣囊和多氦氣囊結構形式，各有利弊，不同形式的氦氣囊結構，決定了不同的放飛和升空過程。在飛艇到達設計高度，進行平飛階段后，無論采用哪種氦氣囊結構形式，其浮重比η都趨近于1，即達到浮重平衡狀態。在飛艇上升過程中，隨著高度增加，不但要排出空氣囊中的空氣以確保艇囊壓差在安全范圍內，也要逐漸排出多余氦氣，以確保飛艇最終的浮重平衡。兩種氦氣囊結構的對比如表2所示。

圖17 兩種氦氣囊結構升速與浮重比關系Fig.17 Comparison of rising velocity and buoyancy-weight ratio between two kinds of helium envelope structure

比較項目單氦氣囊結構多氦氣囊結構氦氣分布同一容腔多個容腔飛艇浮心變化很大，不可控很小，受控升空姿態大仰角小仰角，可選擇放飛時飛艇姿態加速抬頭，尾部下頓仰角不變排氣方式尾部集中排氣分段排氣升速/(m·s-1)5～102～5浮重比小大副氣囊結構簡單復雜加工工藝簡單復雜壓控簡單復雜放飛形式復雜簡單典型案例日本SPF?1美國HALE?D

5 結 論

通過對平流層飛艇在放飛過程中的動力學響應分析，結果表明：

1) 在單氦氣囊結構形式的放飛過程中，飛艇受到的支撐點水平作用力持續增大，支撐點垂直作用力先增大后減小，在放飛后段飛艇尾部必將發生滑動，若采用硬連接方式限制尾部滑動，應充分考慮柔性艇尾的承載能力，確保柔性艇尾的安全。

2) 在多氦氣囊結構形式的放飛過程中，放飛后升速從零開始劇烈波動后收斂較快，仰角變化劇烈，收斂較慢，飛艇以穩定升速升空后，仰角變化逐漸收斂。增大浮重比對飛艇仰角影響較小，但能顯著增大穩定升速。

3) 通過兩種氦氣囊結構形式對比，其各有優缺點：采用單氦氣囊結構形式浮重比較小，可以大仰角快速升空，但仰角變化不可逆不可控，放飛方式復雜；采用多氦氣囊結構形式升空所需凈浮力較大，仰角實時可控可調，壓控與排氣復雜，放飛方式簡單。

4) 通過與飛行試驗數據比較，本文方法能夠滿足工程應用需求，為平流層飛艇放飛方式的選擇和評估提供了理論分析途徑。根據平流層飛艇放飛場實際條件，可對后續的研究進一步細化或區分不同工況：地面風甚至非定常風對飛艇放飛的影響，飛艇行進中放飛動力學，以及將飛艇支撐點代以實際中的苫布或氣墊等，這些分析都可基于本文的計算分析，進行部分方程或條件的增減而完成。

參考文獻 (References)

[1] LIAO L,PASTERNAK I.A review of airship structural research and development[J].Progress in Aerospace Sciences,2009,45(4-5):83-96.

[2] STOCKBRIDGE C,CERUTI A,MARZOCCA P.Airship research and development in the areas of design,structures,dynamics and energy systems[J].International Journal of Aeronautical & Space Sciences,2012,13(2):170-187.

[3] WILSON J R.A new era for airships[J].Aerospace America,2004,42(5):27-31.

[4] STEVE S.The HiSentinel airship[C]∥7th AIAA Aviation Technology,Integration and Operations Conference.Reston:AIAA,2007.

[5] SMITH I,LEE M,FORTNEBERRY M,et al.HiSentinel80:Flight of a high altitude airship[C]∥11th AIAA Aviation Technology,Integration,and Operations Conference.Reston:AIAA,2011.

[6] Lockheed Martin Space System Company High altitude airship[EB/OL].(2014-11-10)[2017-04-13].http:∥www.lockheedmartin.com/us/products/lighter-than-air-vehicles.

[7] GAO.Future aerostat and airship investment decisions drive oversight and coordination needs:GAO-13-81[R].Washington,D.C.:GAO,2012.

[8] JAXA.Ground-to-stratosphere flight test and evaluation of materials and structure for stratospheric airship test vehicle:JAXA-RM-04-012[R].Tokyo:JAXA,2004:7-35.

[9] SHUNICHI O,NOBORU S.R&D status of RFC technology for SPF airship in Japan[C]∥9th Annual International Energy Conversion Engineering Conference.Reston:AIAA,2011.

[10] SELBY C.High altitude airship station keeping and launch model development using output from numerical weather prediction models[D].West Lafayette:Purdue University,2008.

[11] 趙攀峰,王永林,劉傳超.平流層飛艇放飛、回收過程初步分析[J].航空科學技術,2007(4):24-29.

ZHAO P F,WANG Y L,LIU C C.Preparatory analyse on the release and recovery course of stratosphere airship[J].Aeronautical Science and Technology,2007(4):24-29(in Chinese).

[12] 郭虓,祝明,武哲.綜合熱力學模型的平流層飛艇上升軌跡優化[J].北京航空航天大學學報,2012,38(10):1346-1351.

GUO X,ZHU M,WU Z.Ascent trajectory optimization for stratospheric airships with thermal effects[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(10):1346-1351(in Chinese).

[13] 吳雷,李勇,梁棟.平流層飛艇放飛段動力學建模[C]∥第25屆中國控制會議,2006:546-550.

WU L,LI Y,LIANG D.Dynamics modeling on the launch process for a stratospheric airship[C]∥Proceeding of the 25th Chinese Control Conference,2006:546-550(in Chinese).

[14] BLACKINGTON E.United States air force,schriever air force base:AIAA-2003-6005[R].Reston:AIAA,2003.

[15] 周江華.平流層飛艇運動控制律與定點控制律設計[D].北京:中國科學院空間科學與應用中心,2009:22-26.

ZHOU J H.Control law design for motion control and station-keeping control of stratospheric platform airship[D].Beijing:Center for Space Science and Applied Research,Chinese Academy of Sciences,2009:22-26(in Chinese).

[16] CUI Y X,YANG Y C,ZHOU J H,et al.Numerical aerodynamic investigations on stratospheric airships of different tail configurations[C]∥IEEE Aerospace Conference.Piscataway,NJ:IEEE Press,2015:3-4.

[17] KHOURY G,GILLELT J.Airship technology[M].Cambridge:Cambridge University Press,1999:20-23.

[18] LI Y W,NATHON M.Modeling and simulation of airship dynamics[J].Journal of Guidance,Control,and Dynamics,2007,30(6):1691-1700.

[19] 張泰華,姜魯華,張冬輝,等.臨近空間飛艇艇庫外約束及穩定性分析[J].中國空間科學技術,2016,36(5):72-80.

ZHANG T H,JIANG L H,ZHANG D H,et al.Constraint and stability analysis of near space airship outside hangar[J].Chinese Space Science and Technology,2016,36(5):72-80(in Chinese).