變形及電場作用對石墨烯電學特性影響的第一性原理計算?

劉貴立楊忠華

1)(沈陽工業大學力學系,沈陽 110870)

2)(沈陽工業大學建筑環境與能源應用工程系,沈陽 110870)

1 引 言

2004年,英國曼徹斯特大學的Novoselov等[1,2]和Geim研究團隊利用微機械剝離法制備得到了僅由一層碳原子構成的薄片——石墨烯.石墨烯是由單層碳原子緊密堆積成的二維(2D)蜂窩狀結構材料,因其結構簡單、性質奇特而備受關注,迅速成為凝聚態物理、納米科學以及生物技術等前沿學科的交叉研究熱點[3?9].然而石墨烯本身是一個零能隙的半金屬,若要實現傳統半導體的柵極偏壓控制的開關效應等,則需要在石墨烯中打開一定的能隙.若不能實現石墨烯的能隙在一定范圍內的靈活可調,則將嚴重制約其在半導體技術中的實際應用.因此,如何將石墨烯功能化使其產生豐富的能隙具有重要的研究意義.

石墨烯中相鄰碳原子間形成三個σ鍵,剩余一個未成鍵的π電子可以在表面自由移動.石墨烯的電學性質主要由π電子決定[10],而π電子的運動對外力變形非常敏感[11].童國平等[12]研究了拉伸變形對鋸齒形和手扶椅型石墨烯能帶結構的影響,得到了兩種石墨烯π電子能帶及能隙與拉力的解析關系式.Gui等[13]利用第一性原理和緊束縛近似方法分析了不同平面應力下石墨烯的能帶結構.Yu等[14]用分子動力學軟件對含不同晶界的石墨烯進行模擬,研究壓應力條件下對稱傾斜晶界對石墨烯彎曲程度及彎曲變形的影響.Park等[15]利用扭轉變形打開了石墨烯的能隙.但是在石墨烯微電子器件的應用中外加電場對石墨烯性能的影響不可忽略,因為在碳納米管的研究過程中發現,電場對其性質的影響很大.因此,本文利用第一性原理方法,研究在電場作用下變形對石墨烯電學特性影響的電子機理,為提升石墨烯的應用價值提供理論依據.

2 計算方法與模型

本文利用基于密度泛函理論的CASTEP模塊對石墨烯的電學性質進行計算.首先將含有兩個碳原子的石墨烯原胞通過周期性擴展形成3×3×1的超晶胞(圖1(a))來代替石墨烯平面.為防止石墨烯層間的相互影響,添加20 ?的真空層.石墨烯幾何優化的計算參數經過收斂測試確定,采用廣義梯度近似平面波贗勢方法以及Perdew-Burke-Ernzerhof[16]泛函計算電子間的交換關聯勢.為了減少電子體系展開的平面波基數,采用Vanderbilt超軟贗勢[17]描述離子實與價電子之間的相互作用.結構計算中采用Monkhorst-Pack特殊K點取樣方法[18],石墨烯原子模型的K點網格劃分標準為8×8×1.平面波展開的截止能量取為400 eV,并采用Broyden-Fletcher-Goldfarb-Shanno優化算法[19]進行幾何優化,能量的迭代收斂精度為1×10?5eV/atom,原子間相互作用力收斂標準為0.03 eV/?,晶體內應力收斂標準為0.05 GPa,原子最大位移為0.001 ?,自洽場循環收斂為1.0×10?6eV/atom.幾何優化后得到石墨烯C—C原子間的平均鍵長為1.420 ?,與已知結果[20]相符合,說明本文的計算方法可行,參數設置合理.

計算石墨烯的能帶結構及電子態密度使用的第一布里淵區采用閉合路徑G(0,0,0)→M(0,0.5,0)→ K(?0.333,0.667,0)→ G(0,0,0),計算所得本征石墨烯的能帶結構及態密度如圖1(b)所示.能帶結構圖中在費米能級附近存在兩條相切的能帶,即導帶底和價帶頂相重合,能隙為零.總態密度圖可以看作是能帶結構圖的投影,由于費米能級附近本征石墨烯的帶隙為0,故對應的總態密度也呈現出接近0值的情形,這說明本征石墨烯具有零能隙的半金屬特性.這一結果與文獻[9]相一致,從而驗證所建立的計算模型是正確的,可以用于后續的計算.

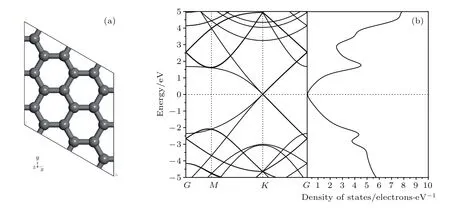
圖1 本征石墨烯的原子結構和電子結構 (a)石墨烯原子模型;(b)能帶結構和態密度Fig.1.Atomic structure and electric structure of intrinsic graphene:(a)Atomic structure of graphene;(b)band structure and density of states.

3 計算結果與分析

3.1 變形對石墨烯能帶結構的影響

在常溫下,石墨烯的邊緣和表面很容易起褶皺,呈現出波動狀態,故石墨烯受到外力作用導致形狀改變的情況是不可避免的.而且石墨烯在電子器件的應用中可以對其施加預應力,這將大大改變石墨烯本身的電子結構和其他性質.因而,本文探討外加力場(變形、電場)對石墨烯電子結構的影響.

圖2所示為對石墨烯施加變形作用,拉伸、剪切變形的施加方法(見圖2(a))為:將石墨烯的兩端碳原子分別沿相反方向施加位移量δ后固定,即紅色碳原子沿±x,±y方向施加位移量δ并固定,其余碳原子呈自由態.拉伸、剪切變形量δ=0.2 ?相當于石墨烯晶格常數(a=b=7.38 ?)的2.7%.對石墨烯施加扭轉變形的方法為:將圖2(a)中的1,2,3號碳原子沿z軸負方向(即向紙面內方向)分別施加0,δ,2δ的位移量,將與之相對的碳原子1′ ,2′ ,3′沿z軸正向(即向紙面外方向)分別施加2δ,δ,0的位移量,位移量δ=0.4 ?相當于石墨烯晶格常數(c=20 ?)的2%,并將移動后的碳原子固定其余碳原子保持自由態;對石墨烯施加彎曲變形的方法如圖2(b)所示,將圖2(b)框中的碳原子沿z軸正向施加δ位移量后固定,位移量δ=0.4 ?相當于石墨烯晶格常數(c=20 ?)的2%,同時將位于石墨烯中部標紅的碳原子固定,這相當于對石墨烯施加彎曲變形作用.

圖2 對石墨烯施加變形作用的示意圖 (a)拉伸、剪切、扭轉變形;(b)彎曲變形Fig.2.Schematic diagram of deformation process of graphene:(a)Stretch,shear and torsion deformation;(b)bending deformation.

幾何優化后,各變形作用下石墨烯的原子結構如圖3所示.

圖3 變形作用下石墨烯的原子結構 (a)剪切變形;(b)拉伸變形;(c)扭轉變形;(d)彎曲變形Fig.3.Atomic structure of deformed graphene:(a)Shear deformation;(b)stretch deformation;(c)torsion deformation;(d)bending deformation.

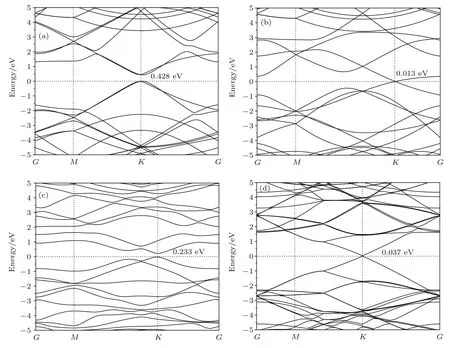
圖4 變形作用下石墨烯的能帶結構 (a)剪切變形;(b)拉伸變形;(c)扭轉變形;(d)彎曲變形Fig.4.Band structure of deformed graphene:(a)Shear deformation;(b)stretch deformation;(c)torsion deformation;(d)bending deformation.

圖4所示為變形作用下石墨烯的能帶結構.圖4(a)可見,剪切變形下石墨烯的導帶底和價帶頂相對,存在直接帶隙.與本征石墨烯相比,剪切變形使得石墨烯的導帶底向高能區方向移動,導致能隙增加至0.428 eV,由半金屬性質向半導體性質轉變,實現了石墨烯能隙寬度的調控;拉伸變形對石墨烯的電子結構影響不大(見圖4(b)),僅產生0.013 eV的微小帶隙;扭轉變形使得石墨烯的能隙增加至0.233 eV(見圖4(c));而彎曲變形對石墨烯能隙的影響可忽略不計(見圖4(d)).

綜上所述,對石墨烯施加變形作用相當于施加外力作用,這能夠引起原子的不規則運動,使得電荷重新分布,進而導致石墨烯能隙的變化.剪切變形、扭轉變形能夠打開石墨烯能隙,實現石墨烯在分子開關、半導體器件等方面的應用.但石墨烯能隙對拉伸變形、彎曲變形不甚敏感.特別是拉伸變形作用,計算發現即使進一步提高拉伸變形量,以至原子間成鍵穩定性被破壞,幾何優化無法收斂至穩定態,也只存在微小能隙.故利用剪切變形和扭轉變形是利用變形調控石墨烯能隙的首選手段.

3.2 外加電場對石墨烯能帶結構的影響

施加的外部電場也可以認為是一個力場,能夠引起石墨烯能隙的變化.本節首先將電場強度確定為0.5 eV/?/e,分別考察〈100〉,〈010〉,〈001〉,〈110〉等電場方向對石墨烯能隙的影響.圖5為不同方向電場作用下石墨烯的能帶結構,可見石墨烯能隙會對平行其平面方向的電場較為敏感,而對垂直其平面方向的電場不敏感;不同方向的平行于石墨烯平面的外加電場對能隙的影響也不同,在xy平面內沿y方向施加電場,打開能隙的效果最為明顯.

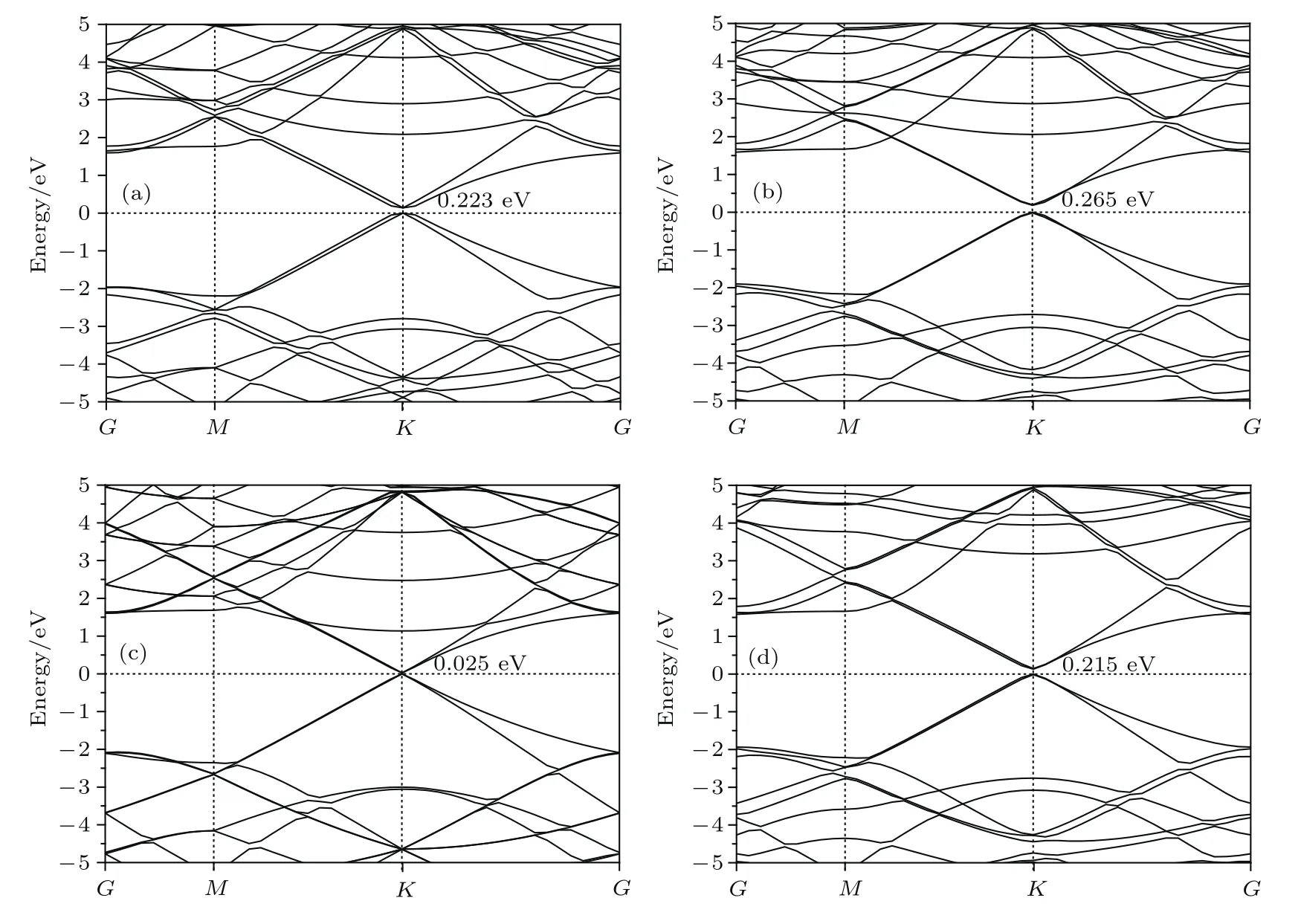
圖5 不同方向電場作用下石墨烯的能帶結構 (a)電場方向〈100〉;(b)電場方向〈010〉;(c)電場方向〈001〉;(d)電場方向〈110〉Fig.5.Band structure of graphene in electric f i elds of different directions:(a)Electric f i eld direction〈100〉;(b)electric f i eld direction〈010〉;(c)electric f i eld direction〈001〉;(d)electric f i eld direction〈110〉.

如表1所列,電場方向對石墨烯系統總能及布居數的影響,不同的電場方向下石墨烯的系統總能不同.〈010〉電場方向下的系統總能最低,〈100〉和〈110〉電場方向下的系統總能次之,而〈001〉電場方向下的系統總能最高.由此可知,不同電場方向下石墨烯的系統穩定性由高至低的變化規律與不同電場方向下的石墨烯能隙寬度由大至小的變化規律相符合,說明石墨烯原子間的鍵能與能隙寬度間存在一定的聯系.布居數值反映原子間的成鍵作用,正值表征原子間呈共價鍵相互作用,負值表征原子間呈反鍵相互作用.〈010〉電場方向下石墨烯C—C原子間的布居數正值數值較大,成鍵鍵能較高,系統總能較低進而穩定性較好.同時,C—C原子間布居數負值數值較小,反鍵鍵能較低.因為成鍵態主要形成價帶,反鍵態主要形成導帶,而能隙為價帶和導帶間的差值,故〈010〉電場方向下石墨烯的能隙較大;〈001〉方向下石墨烯C—C原子間的布居數正值數值較低,負值數值較高,故成鍵鍵能較低,反鍵鍵能較高,系統總能較高,能隙較小.

表1 電場方向對石墨烯系統總能及布居數的影響Table 1.Influence of electric f i eld direction on total system energy and population of graphene.

設置不同的電場強度,沿平行于石墨烯平面的y方向施加電場,考察電場強度與能隙寬度的變化規律.圖6所示為電場強度對石墨烯能隙的影響,電場強度(E)從0.1 eV/?/e增加至0.5 eV/?/e,石墨烯的能隙依次增加,總體上呈線性增長勢.

圖6 不同電場強度對石墨烯能隙的影響Fig.6.Influence of electric f i eld strength on energy gap of graphene.

3.3 外加電場及變形共同作用對石墨烯能帶結構的影響

變形及電場都可以看成為外加力場,影響石墨烯的電子結構從而導致能隙的變化.電場強度對本征石墨烯的能隙(0.056 eV)影響較微弱,在此電場強度下對石墨烯施加剪切、拉伸、扭轉和彎曲等變形作用,考察電場及變形共同作用對石墨烯能隙的影響,結果見表2.

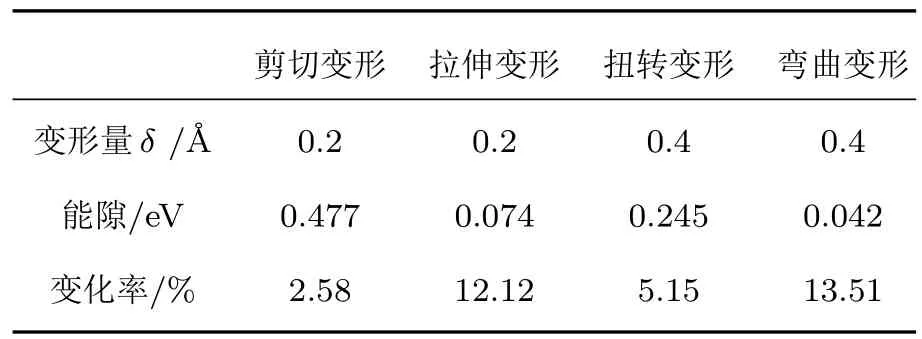
表2 外加電場及變形共同作用對石墨烯能帶結構的影響Table 2.Influence of external electric f i eld and combined deformation on band structure of graphene.

由表2可見,外加電場提高了變形對打開石墨烯能隙的作用效果.相對而言,外加電場對拉伸與彎曲變形的作用效果較明顯.但無論何種變形,石墨烯能隙的打開效果均不及電場與變形兩種外場疊加的作用效果.

4 結 論

利用第一性原理方法,對變形及電場作用下石墨烯的電子結構進行了研究.結果表明,費米能級附近本征石墨烯的能隙及態密度值均為0,呈現出半金屬特性;剪切變形和扭轉變形打開石墨烯能隙的作用明顯,而拉伸變形和彎曲變形對石墨烯的能隙作用可忽略不計;不同的電場方向對石墨烯能隙的影響不同,〈010〉電場方向對打開石墨烯能隙的作用效果最強,而〈001〉電場方向的作用效果最弱.這是因為〈010〉電場方向下石墨烯C—C原子間的布居數正值較大,成鍵鍵能較高.而布居數負值數值較小,反鍵鍵能較低;電場強度從0.1 eV/?/e增加至0.5 eV/?/e,石墨烯的能隙呈線性增長勢;共同作用下外加電場提高了變形對打開石墨烯能隙的作用效果,但均不及電場與變形兩種外場疊加的作用效果.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva V,Firsov A A 2004Science306 666

[2]Novoselov K S,Jiang D,Schedin F,Booth T J,Khotkevich W,Morozov S V,Geim A K 2005Proc.Natl.Acad.Sci.USA102 10451

[3]Zhang Y B,Tan Y W,Stormer H L,Kim P 2005Nature438 201

[4]Ney A,Papakonstantinou P,Kumar A,Shang N G,Peng N 2011Appl.Phys.Lett.99 102504

[5]Nair R R,Sepioni M,Tsai I L,Lehtinen O,Keinonen J,Krasheninnikov A V,Thomson T,Geim A K,Grigorieva I V 2012Nat.Phys.8 199

[6]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009Rev.Mod.Phys.81 109

[7]He J,Chen K Q,Fan Z Q,Tang L M,Hu W P T 2010Appl.Phys.Lett.97 193305

[8]Sun L F,Fang C,Liang T X 2013Chin.Phys.Lett.30 047201

[9]Zhou S,Liu G,Fan D 2017Phys.B:Condens.Matter506 156

[10]Prezzi D,Varsano D,Ruini A,Marini A,Molinari E 2008Phys.Rev.B77 041404

[11]Liao W H 2010Ph.D.Dissertation(Hunan:Hunan Normal University)(in Chinese)[廖文虎 2010博士學位論文(湖南:湖南師范大學)]

[12]Wei Y,Tong G P 2009Acta Phys.Sin.58 1931(in Chinese)[韋勇,童國平 2009物理學報 58 1931]

[13]Gui G,Li J,Zhong J X 2008Phys.Rev.B78 075435

[14]Yu J,Zhang X X,Ji J S,Huang D,Xi W 2015Chin.J.Nonferrous Met.25 3452

[15]Park J S,Choi H J 2015Phys.Rev.B:Condens.Matter Mat.Phys.92 045402

[16]Perdew J P,Burke K,Ernzerhof M 1996Phys.Rev.Lett.77 3865

[17]Vanderbilt D 1990Phys.Rev.B:Condens.Matter41 7892

[18]Monkhorst H J,Pack J D 1976Phys.Rev.B135 188

[19]Shanno D F 1970Math.Comput.24 647

[20]Han T W,He P F 2010Acta Phys.Sin.59 3408(in Chinese)[韓同偉,賀鵬飛 2010物理學報 59 3408]