基于改進廣義S變換的Q值提取及應用

施 羽， 巫南克， 周懷來,b,c， 王 聰

(成都理工大學 a.地球物理學院，b.“油氣藏地質及開發工程”國家重點實驗室，c. “地球探測與信息技術”教育部重點實驗室，成都 610059)

0 引言

彈性波在地下介質中傳播時，地層的非均質性引起的衰減是一種基本現象，品質因子Q常被用來定量描述這種現象。品質因子Q是檢驗地層是否飽含油氣的一個重要標志，也是描述巖石彈性的重要參數之一，與介質內部的結構特征和介質的飽和度、孔隙度、滲透率等流體性質都緊密相關[1-3]。所以求取準確的Q值可以為井位選取、油氣檢測、儲層預測等提供有用且可靠的參考信息。

當從反射地震記錄中提取Q值時，目前主要有三種頻率域方法已被人們廣泛使用：①譜比法(SR)[4];②質心頻率偏移法(CFS)[5];③峰值頻率偏移法(PFS)[6]。其中譜比法基于地層吸收造成的子波能量衰減求取Q值，原理簡單，適用性強，但是對地震數據質量要求高，易受噪聲影響。質心頻率偏移法和峰值頻率偏移法都是基于吸收衰減所造成的子波頻率成分變化求取Q值，方法簡單高效，但是也受地震數據質量限制。王陽華[7-9]通過構造時頻函數將時頻譜轉換為一維數據并通過補償分析求取Q值，該方法雖穩定但較為繁瑣；Singleton[10]提出Gabor-Morlet連接時間頻率分析方法； Hu等[11]提出一種改進的頻率偏移法， Qian Wang等[12]在這種方法基礎上加以改進，這幾種方法均需通過時頻轉換來求取Q值。近年來，從時頻域估計Q值的方法不斷發展。王小杰等[13]基于S變換從S域時頻譜估計地層Q值，該方法有效克服了傳統譜比法抗噪能力差、受薄層調諧作用影響等缺點；但是S變化時窗固定不能根據頻率成分靈活調節，導致其時頻聚焦性不足從而影響Q值估計準確性。付勛勛等[14]基于改進的廣義S變換提取地層頂底界面瞬時頻譜求取Q值，與傳統的頻譜比法相比，通過時頻域求取地層Q值計算精度較高，然而在實際應用中地層頂底界面瞬時頻譜不易準確提取。筆者基于Zhou[15]提出的改進廣義S變換應用譜比法從時頻域估計Q值，該方法在保留譜比法適用性強等優點的同時,利用時頻域能量集中部分作比估計地層平均Q值，無需拾取瞬時頻譜或利用單個子波作比，成功提高了Q值估計的穩定性。

1 基本原理

1.1 譜比法

地震波在粘彈性非均勻介質中傳播時，地震波能量會隨時間衰減，經過旅行時t后對應的振幅可表示為式(1)。

(1)

式中:A0(f)是初始時刻地震波的振幅譜；B(t)是反射系數、幾何擴散等因素相關的因子(與頻率無關)，代表其他因素對地震波吸收衰減的影響；f是地震波的頻率；t為傳播時間。這里振幅衰減是由單個的頻率所影響的。圖1(a)表示主頻為35 Hz的雷克子波，在不同Q值的衰減介質中傳播0.2 s后所觀察到的振幅變化，圖1(b)為子波經衰減后所對應的振幅譜。通過觀察圖1發現：當子波通過衰減介質時，振幅能量會發生衰減，且Q值越小衰減越大，即低Q值高衰減；高頻能量較低頻能量衰減更快，質心頻率向低頻偏移[16]。

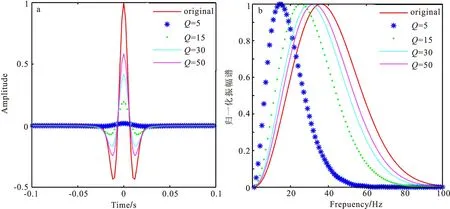
圖1 雷克子波在不同Q值的衰減介質中傳播0.2 s后所得結果Fig.1 The results of Ricker wavelet in different Q value medium propagate of 0.2 s(a)雷克子波；(b)歸一化振幅譜

基于等式(1)，得到式(2)。

(2)

式中:C是與頻率無關的常數,Q值可以由有效頻帶范圍內的兩個振幅譜作比求對數，然后同對應頻率做最小二乘擬合所導出。

頻率域Q值估計方法均需從記錄中拾取子波從而求取Q值，但這樣容易受到相鄰子波和環境噪聲影響，導致Q值求取不穩定。如圖2所示，從信噪比為10 dB的地震記錄中拾取紅色時窗內單個子波并求取子波振幅譜。從圖2可以發現，子波受噪聲和相鄰子波影響嚴重，和單個理想子波振幅譜相比有較大誤差，這樣便導致頻率域Q值估計方法不夠穩定。

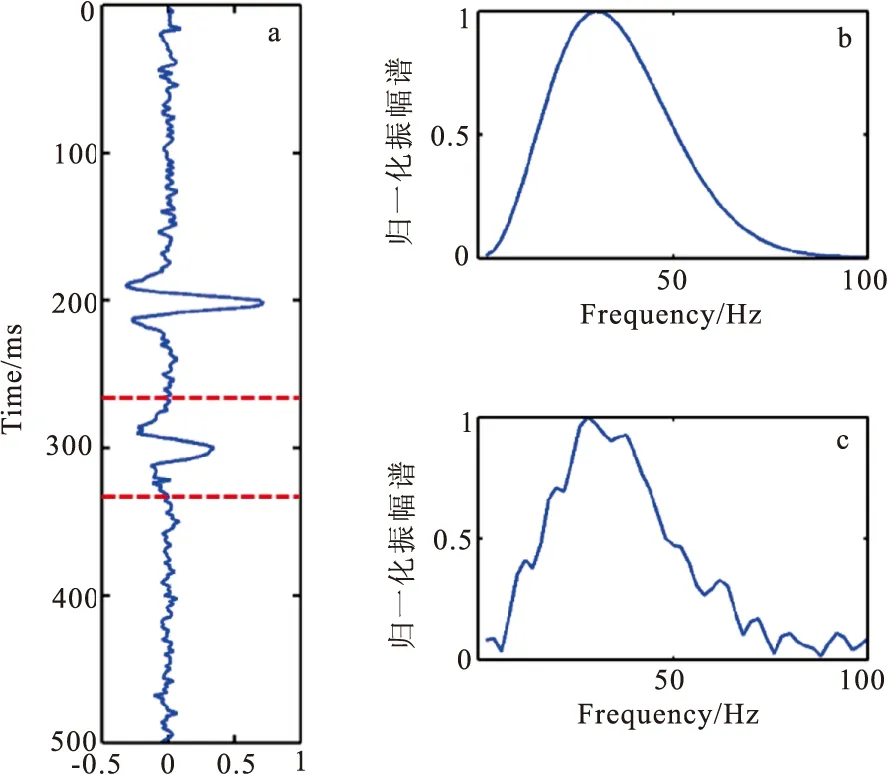
圖2 頻率域Q值估計方法子波提取Fig.2 Frequency domain Q estimation wavelet extraction(a)信噪比為10 dB地震記錄；(b)理想子波振幅譜；(c)紅色時窗內子波振幅譜

1.2 S域衰減估計

王小杰等[13]、付勛勛等[14]基于S變換從S域時頻譜估計地層Q值。作為時頻域的一種Q值估計方法，該方法有效克服了傳統譜比法抗噪能力差、受薄層調諧作用影響等缺點；但是S變化時窗固定不能根據頻率成分靈活調節，導致其時頻聚焦性不足，且在實際應用中地層頂底界面瞬時頻譜不易準確提取，從而影響Q值估計準確性。

假設地震波到目標層上、下界面所用的旅行時分別為t1和t2，t1、t2時刻對應的地震信號S域瞬時頻譜分別為S(t1,f)和S(t2,f)，則地層Q值可通過式(3)得到。

(3)

其中：p為斜率；f為頻率。

(4)

1.3 基于改進廣義S變換的Q值提取法

筆者采用改進廣義S變換取代傅里葉變換在時頻域應用譜比法求取Q值(AGSSR)，該方法在保留譜比法適用性強等優點的同時，利用時頻域能量集中部分作比估計地層平均Q值，無需拾取瞬時頻譜或利用單個子波作比，成功提高了Q值估計的穩定性。

廣義S變換在時頻分析中有很高的靈活性，可以根據實際情況調節尺度參數，從而得到最佳的時頻分辨率，這樣在時頻域Q值估計中便能較準確地判斷子波時域位置和頻域成分。將改進廣義S變換和譜比法相結合，得到一種從時頻域估計Q值的方法(AGSSR)，具體方法如下：

首先，對地震記錄u(t)做廣義S變換得到時變頻譜U(τ,f)，其中τ為時間，f為頻率。

(5)

式中:r和σ''為尺度參數，可以根據實際情況靈活調節其大小，最終使處理效果達到最佳。

只考慮吸收衰減，其時變振幅譜為式(6)。

(6)

然后，利用時頻域振幅能量集中部分采用譜比法對應作比求取Q值：

(7)

式中:tj為時間；τi為取樣間隔；Δtj為時間間隔。最后，分別求取各層的平均Q值：

(8)

圖3為時頻域Q值提取法過程示意圖，首先對記錄(圖3(a))進行廣義S變換得到時頻譜(圖3(b)), 然后利用時頻譜能量集中部分采用譜比法分別作比得到Qji，最后求取各層平均Q值。

圖3 時頻域Q值提取法過程示意圖Fig.3 AGSSR process diagram(a)信噪比為10 dB地震記錄；(b)圖3(a)記錄的時頻譜；(c)t=300 ms時刻的振幅譜

2 合成記錄測試

給定一個多層模型，各層Q值依次設為100、50、20、70。采用主頻為35 Hz的雷克子波與地層模型褶積得到衰減合成記錄，如圖4(a)所示。

為了對比分析譜比法(SR)、S域衰減估計(SSR)、利用目標層頂底界面瞬時頻譜作比的廣義S變換衰減估計(IGSSR)，以及基于改進廣義S變換求取地層平均Q值(AGSSR)等四種Q值估計方法的抗噪能力，筆者采用這四種方法從不同信噪比的記錄中提取Q值，并做誤差分析。

分別從無噪地震記錄(圖4(a))中提取Q值，四種方法都能得到準確的Q值，如表1所示。(本文中Mean為同一信噪比情況下計算10次得到的平均Q值，σ為標準差，下同。)

當從信噪比較高的記錄中提取Q值時，四種方法計算得到的Q值如表2所示，其中SSR、IGSSR、AGSSR求取Q值較為穩定，受噪聲影響最小；而譜比法(SR)受噪聲影響較大。

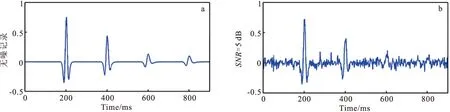
圖4 合成地震記錄Fig.4 Seismic synthetic record(a)信噪比衰減記錄；(b)信噪比為5 dB的衰減記錄

當合成記錄信噪比較低時(圖4(b))，AGSSR穩定性明顯優于其他三種Q值估計方法。但是，由于合成記錄信噪比較低，導致四種方法都不能得到準確可靠的Q值，標準差都較大，平均值也不夠準確(表3)。

綜上所述，四種方法中AGSSR抗噪能力優于其他三種Q值估計方法，方法最為穩定；而其他三種方法中時頻域Q值估計方法(SSR、IGSSR)較頻率域Q值估計方法(SR)有更好的抗噪能力，方法更為穩定。

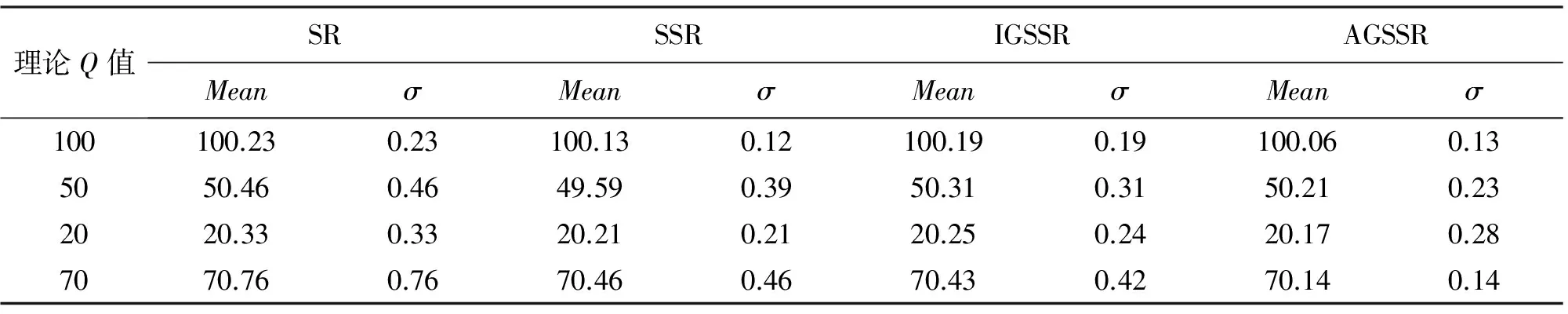
表1 無噪地震信號采用四種方法求取的Q值

表2 信噪比為50 dB的地震信號采用四種方法求取的Q值

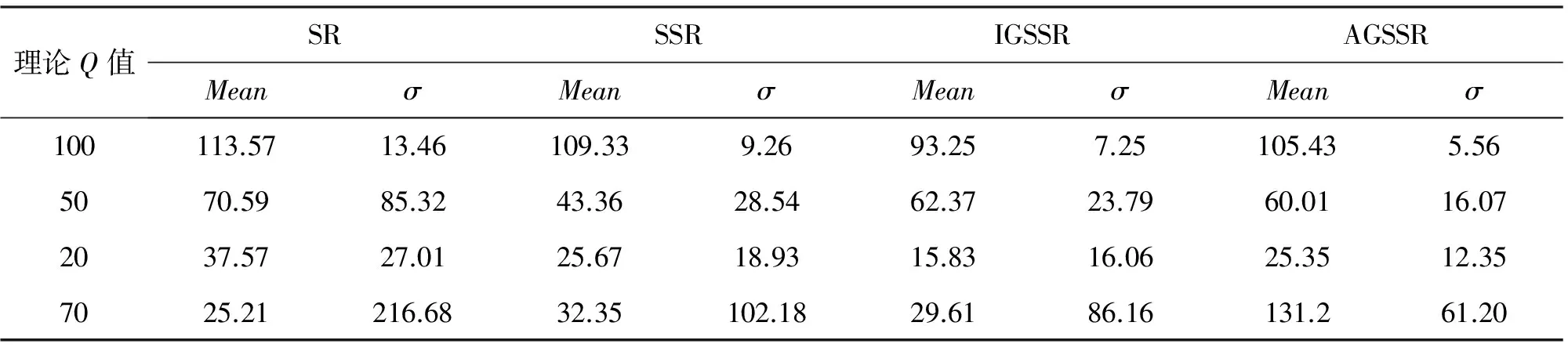
表3 信噪比為5 dB的地震信號采用四種方法求取的Q值

3 實際資料應用

將基于改進廣義S變換的Q值提取方法，運用到西部某工區實際地震資料中，加以驗證該方法的適用性和穩定性。圖5為過井地震剖面，目標層位置在圖中兩紅色虛線之間，該層位裂縫發育，孔隙性良好，是有利的油氣儲集層。根據后期所反饋的信息，圖5中井為高產氣井，目標層段為油氣儲集層段。圖6(a)為單獨提取出的第160道地震記錄，該記錄位于井旁。對記錄進行廣義S變換得到時頻譜(圖6(b))，然后應用時頻譜能量集中部分作比求取該道記錄層狀平均Q值，結果如圖6(c)所示。對結果進行分析，可以發現，在2.6 s～2.7 s之間地層平均Q值明顯低于其余層段，對比實際剖面發現該時間段與目標層段吻合。圖7是對2.6 s～2.7 s時間段求取的平均Q值，如圖7所示，在第100道～200道之間出現了相對的低Q值，這與目標層段相吻合。圖8為運用本文Q值提取法求取的全剖面Q值分布情況，圖8中綠色為高Q值，紅色為低Q值。圖8中兩紅色虛線之間為低Q層段，這與目標層段吻合，為油氣聚集層段。

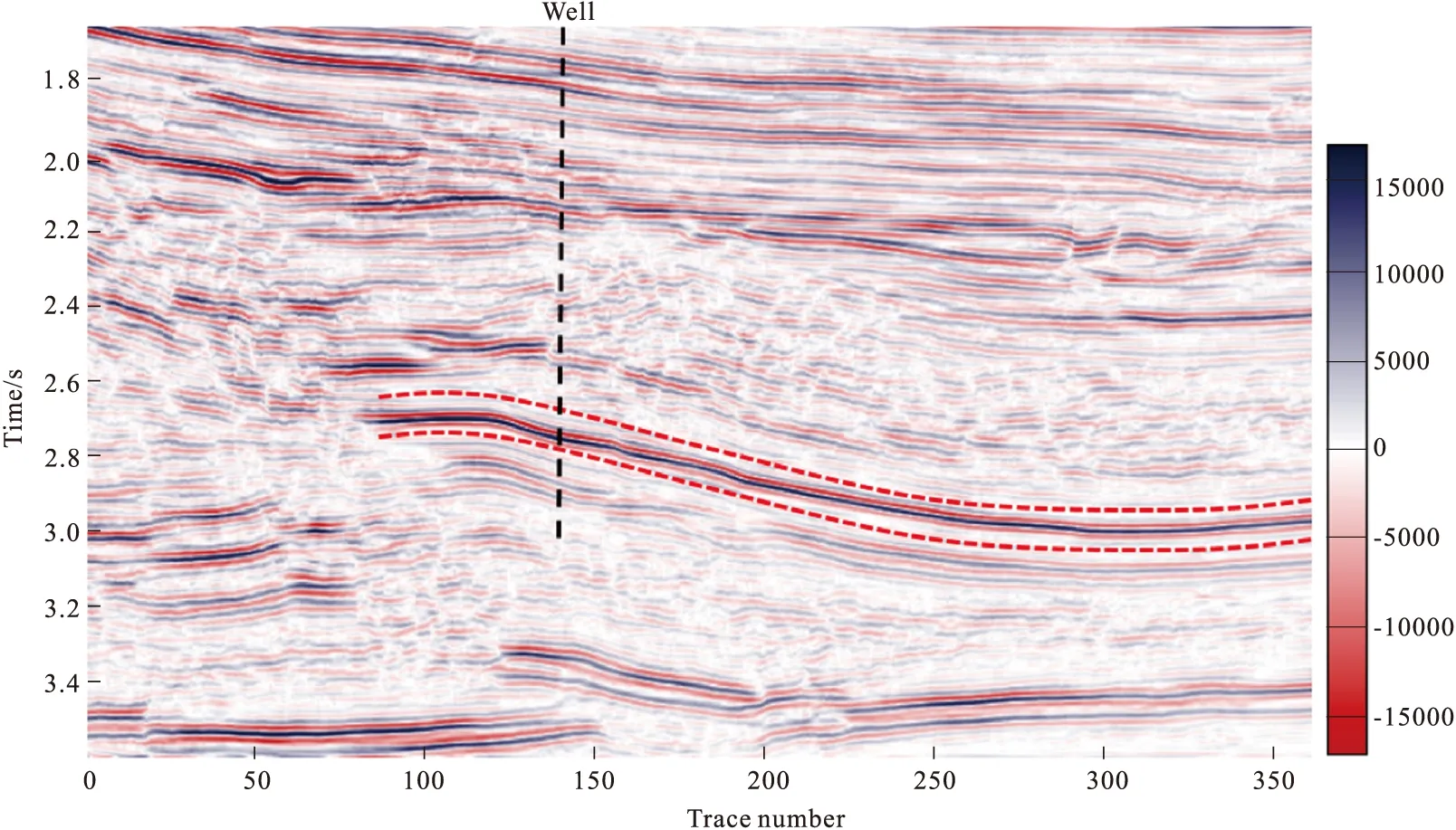
圖5 過井剖面Fig.5 Connecting-well section

圖6 單道記錄Q值求取Fig.6 Single-channel recording Q value estimate(a)單道地震記錄；(b)記錄時頻譜；(c)Q值

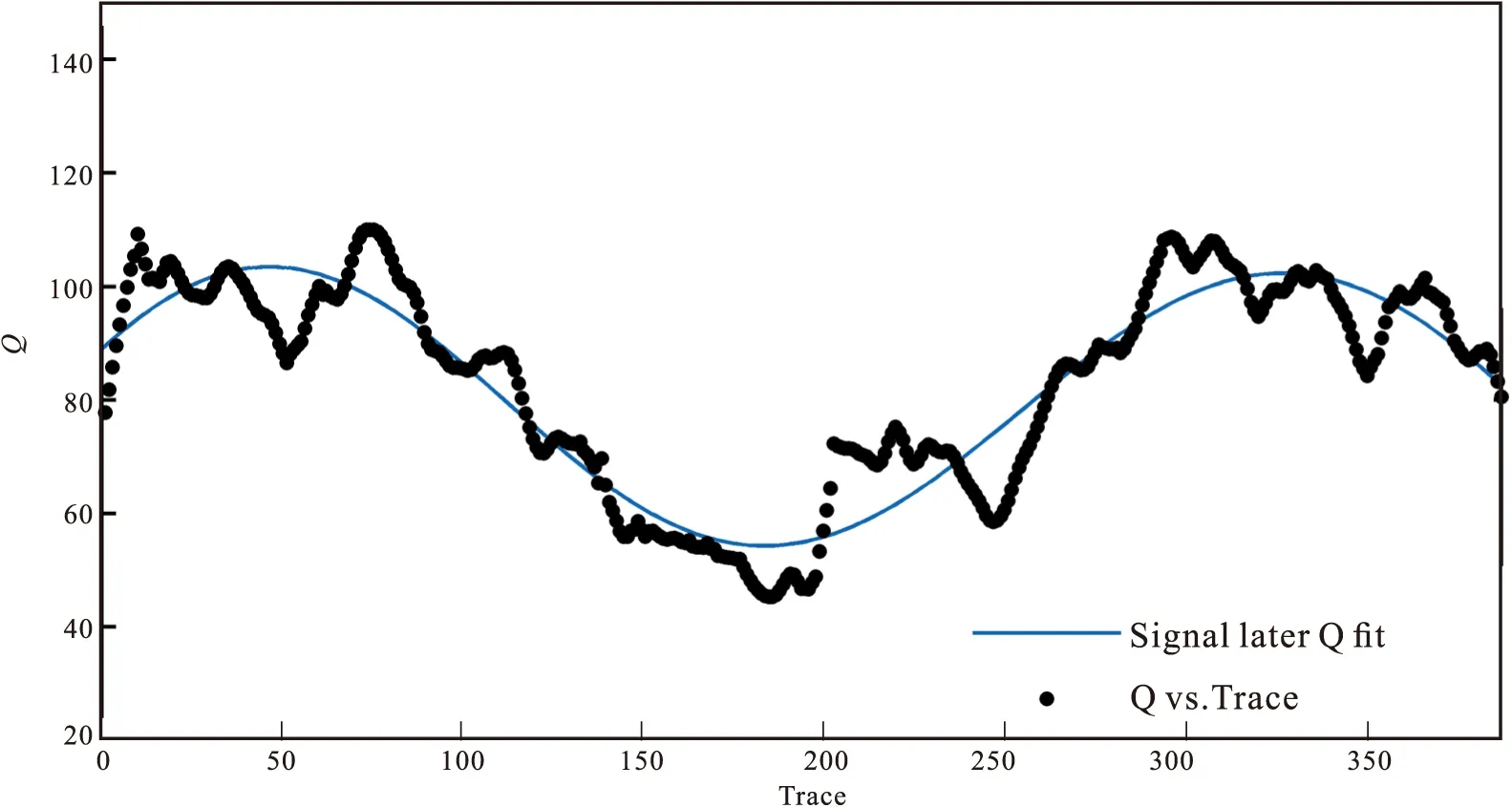
圖7 t=2.6 s～2.7 s時段平均Q值擬合曲線Fig.7 t = 2.6 s to 2.7 s time average Q value curve fitting

圖8 Q值估計圖Fig.8 The estimate of Q

綜上所述，將改進的廣義S變換與譜比法相結合，采用時頻譜能量集中部分對應作比估計平均Q值的方法是有效可行的。

4 結論

常用的頻率域Q值估計方法，均需從地震記錄中拾取子波從而求取Q值，但這樣容易受到相鄰子波和環境噪聲的影響，導致Q值求取不穩定。在常規時頻域Q值估計方法中S變化時窗固定不能根據頻率成分靈活調節，導致其時頻聚焦性不足，且在實際應用中地層頂、底界面瞬時頻譜不易準確提取，從而影響Q值估計準確性。筆者采用改進的廣義S變換取代傅里葉變換在時頻域應用譜比法提取Q值，該方法在保留譜比法適用性強等優點的同時，應用時頻域能量集中部分對應作比估計平均Q值，無需拾取瞬時頻譜或利用單個子波作比，成功提高了Q值估計的穩定性。通過模型試驗和實際資料應用，結果證明該方法是一種有效可行的Q值估計方法。

參考文獻：

[1] 宮同舉，孫成禹. 幾種提取品質因子方法的對比分析[J]. 勘探地球物理進展，2009(4):252-256.

GONG T J, SUN C Y. Contrastive analysis several quality factor extraction methods [J]. Progress in exploration geophysics，2009(4):252-256.(In Chinese)

[2] 馬昭軍, 劉洋. 地震波衰減反演研究綜述[J]. 地球物理學進展,2005，20(4):1074-1082.

MA S J,LIU Y. Review of seismic wave attenuation inversion[J]. Progress in Geophysics , 2005, 20(4): 1074-1082. (In Chinese)

[3] 尹陳，賀振華，黃德濟. 基于波動方程的地震波衰減理論研究及應用[J]. 成都理工大學學報(自然科學版),2008(3):263-267.

YIN C,HE Z H,HUANG D J.Based on the wave equation of seismic wave attenuation theory research and application[J].Journal of chengdu university of technology (Natural Science Edition),2008(3):263-267.(In Chinese)

[4] BATH M . Spectral analysis in geophysics [M]. New York: Elsevier, 1974.

[5] QUAN Y L, HARRIS J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997(62):895-905.

[6] ZHANG C J,ULRYCH T J.Estimation of quality factor from CMP records[J].Geophysics,2002(67):1542-47.

[7] WANG Y.Seismic inverseQfiltering[M].UK:BlackwellPublishing,2008.

[8] WANG Y . StableQanalysis on vertical seismic profiling data[J]. Geophysics,2014, 79(4):D217-D225.

[9] WANG Y . Frequencies of the Ricker wavelet[J]. Geophysics,2015, 80(2):A31-A37.

[10] SINGLETON S, TANER M T ,TREITEL S.Qestimation using Gabor-Morlet joint time-frequency analysis techniques[C]. SEG Extended Abstracts, 2006(25):1610-1614.

[11] HU C H, TU N, LU W K. Seismic attenuation estimation using an improved frequency shift method[J]. IEEE Geoscience and Remote sensing Letters, 2013,10(5):1026-1030.

[12] QIAN WAMG.Qestimation with improved frequency shift method based on generalized seismic wavelet[C]. SEG 2016,International Exposition and 86th Annual Meeting,2016:3016-3020.

[13] 王小杰，印興耀,吳國忱，等. 基于S變換的吸收衰減技術在含氣儲層預測中的應用研究[J]. 石油物探，2012, 51(1):37-42.

WANG X J, YING X Y,WU G C, et al. The application of an S transform based absorption and attenuation technique for prediction of gas-baring reservoir[J]. GPP, 2012, 51(1):37-42. (In Chinese)

[14] 付勛勛，徐峰,等. 基于改進的廣義S變換求取地層品質因子Q值[J]. 石油地球物理勘探，2012,47(3)：457-461.

FU X X, XU F, et al. Eastimation of quality factor based on improved generalized S-transform[J]. OGP, 2012, 47(3)：457-461. (In Chinese)

[15] HUAILAI ZHOU, CANGCHENG WANG,KURT J.MARFURT,et al.Enhancing the resolution of nonstationary seismic data using improved time-frequency spectral modeling[J].Geophysical Journal International,2016, 205,203-219.Doi:10.1093/gji/ggv5

[16] 張固瀾. 地震波吸收特性及應用研究[D].成都:成都理工大學,2008.

ZHANG G L. Seismic wave absorbing properties and Application research [D].Chengdu:Chengdu university of technology, 2008. (In Chinese)