決策問題的分解處理方法

閆 碩 張云勇 嚴斌峰 加雄偉

1中國聯合網絡通信集團有限公司100033北京

2北京郵電大學計算機學院100876北京

3中國聯合網絡通信有限公司研究院100176北京

引言

智能信息的處理，常常涉及數據信息的決策問題，使數據信息與決策問題的聯系成為關注的課題。數據信息的決策過程往往概括為：在數據滿足相關條件的前提下，數據應對結論的判定。這不僅是數據智能處理研究的課題，也在實際當中經常涉及。所以針對數據決策的研究具有理論和應用方面的意義，由此引出本文的討論，如下的工作將面對數據決策相關的問題。

數據決策問題與數據的性質密切相關，決策過程將根據數據滿足的特性，確定數據應對的結論，由此引出的數據決策問題必然涉及數據特性之間的因果關系，以及相關的描述或表示。因此建立數據特性的描述方法，構成討論的研究環境，是工作得以展開的基礎。

實際上，數據處理涉及的決策系統[1-2]是與決策問題密切相關的結構化表示形式。決策系統匯集了數據滿足前提，對應結論的決策信息。作為數據處理的研究課題，決策系統的研究涉及屬性約簡[3-5]、數據關聯[6-7]、數據推理[8-10]、數據合并[11]等課題或方向，并獲得了有意義的成果。不過這些討論并不直接針對數據決策的因果聯系，如何對決策系統記錄的決策信息刻畫描述，明確決策概念的含義也未在這些討論中涉及。因此由數據特性引出的決策問題為決策系統的研究預留了空間，以下針對的正是這方面的問題。

為此，回顧決策系統的結構組成是必要的，即：決策系統匯集了數據以及數據的各類屬性信息，構成了相關對象的結構化表示。如果把決策系統作為參照的模型，實施對樣本的判定，比對樣本數據滿足的性質，確定其應對的結論，則決策系統將支撐決策方法的產生，因此對樣本給予專門的討論是需要考慮的問題。盡管樣本在機器學習[12-13]中頻繁涉及，但因為問題的不同，樣本在不同的討論中具有自身的形式，存在著一定的差異。所以基于決策系統的比對判定，對樣本具有結構上的要求，下面的討論將明確樣本的形式。

決策系統記錄的數據和相關的性質將體現條件信息和決策信息組合在一起的因果聯系。所以與決策系統相關的樣本必然基于決策系統包含的信息，由此體現決策信息的組合，刻畫決策判定的含義，應對判定方法的建立。進而，為使決策判定清晰簡化，判定方法將涉及復雜問題的分解處理。下面的討論將圍繞這些方面展開，由此形成自身的方法體系。

1 決策系統與決策問題

上述的討論表明決策系統由各類信息組合而成，搭建了數據性質之間的因果聯系，形成了決策問題的研究前提。如果把決策系統作為參照的模型，對給定的樣本實施決策判定，那么熟悉了解決策系統的構成是必需的。

1.1 決策系統

決策系統以數學結構的形式匯集了數據和數據的屬性信息，其通過判定數據的性質，得到相應結論的結構化表示為決策問題智能化處理提供了參照依據。決策系統以DS=(U，A，V，f)的形式進行表示，其中的U、A和V都是集合，f是一函數，其含義解釋如下。

U是一有限集，稱為論域，U中的元素稱為數據。

A也是一有限集，其元素稱為屬性，所以A稱為屬性集，滿足A=C∪D及C∩D=?，這里的C和D也都是屬性集，C稱為條件屬性集，其中的元素稱為條件屬性；D稱為決策屬性集，其中的元素稱為決策屬性。

V是一有限集合，由A中屬性取得的值構成。V稱為屬性值域，其中的元素稱為屬性值。

f∶U×A→V是從U×A到V的函數，稱為信息函數。對于∈U×A，存在唯一的v∈V，使得f(x，a)=v。

對于決策系統DS=(U，A，V，f)，考慮屬性a∈A，當x∈U時，有∈U×A，所以存在唯一的v∈V，使得f(x，a)=v。此表達式f(x，a)=v可以記作a(x)=v(=f(x，a))。由此可知屬性集A中的屬性a是從U到V的函數，稱為屬性函數。當a是條件屬性時，稱a為條件屬性函數；當a是決策屬性時，稱a為決策屬性函數。

決策系統可以采用表格的形式予以直觀的表示，稱為決策表，如表1所示。

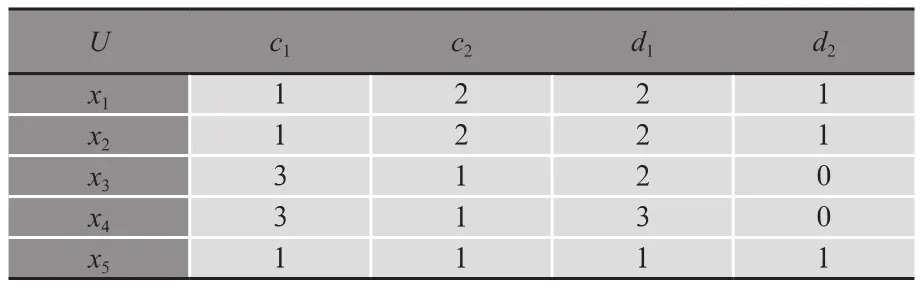
表1 決策系統DS

該決策表表明了決策系統DS=(U，A，V，f)的各個組成部分，其中論域U={x1，x2，x3，x4，x5}包含5個數據；屬性集A=C∪D由條件屬性集C={c1，c2}和決策屬性集D={d1，d2}構成；屬性值域V={0，1，2，3}由有限個數值構成；信息函數f的取值已在表1中展示，如f(x1，c1)=1，f(x4，c2)=1，f(x4，d2)=0等等，這些函數表達式還可表示為c1(x1)=1(=f(x1，c1))；c2(x4)=1(=f(x4，c2))；d2(x4)=0(=f(x4，d2))等。

在表1的決策系統中，論域U={x1，x2，x3，x4，x5}中僅給出5個數據，條件屬性集C={c1，c2}和決策屬性集D={d1，d2}分別給出了兩個條件屬性c1和c2，及兩個決策屬性d1和d2。一般情況下，決策系統DS=(U，A，V，f)的論域U往往包含大量的數據，條件屬性和決策屬性也非個位數計之，決策系統DS=(U，A，V，f)往往構成龐大的數據庫系統。巨大的數據信息可能會對基于決策系統的數據處理或問題決策造成障礙，特別當屬性集A=C∪D中的屬性眾多時，可能使相關的決策變得含混不清，或使決策無所適從。

因此給出一種處理方法，使依據決策系統產生的決策清晰可行，且容易對決策的結果進行判斷是值得考慮的課題。如下將展開這方面的討論，這需要分析決策系統的功能，明確決策系統的作用。為此引入與決策系統相關的概念，以求討論的嚴謹分明。

1)條件函數值：對于屬性a∈A，若x∈U且a(x)=v，則當a是條件屬性函數時，稱v為條件函數值。

2)決策函數值：對于屬性a∈A，若x∈U且a(x)=v，則當a是決策屬性函數時，稱v為決策函數值。

3)樣本：在決策系統DS=(U，A，V，f)對應的決策表中，U中數據x對應的行稱為決策系統的樣本，簡稱樣本，并采用向量(x，u1，u2，…，um；v1，v2，…，vn)進行表示，其中x是論域U中的數據，u1，u2，…，um(m≥1)是與x相關的所有條件函數值，v1，v2，…，vn(n≥1)是與x相關的所有決策函數值，并用分號“；”把條件函數值和決策函數值分開。

4)樣本數據：在樣本(x，u1，u2，…，um；v1，v2，…，vn)中，稱x為樣本數據，樣本數據就是論域U中的數據。

5)同型樣本：如果兩個樣本的條件函數值的個數相同，同時決策函數值的個數也相同，則稱這兩個樣本是同型樣本。比如(x，u1，u2，…，um；v1，v2，…，vn)和(y，w1，w2，…，wm；z1，z2，…，zn)是同型樣本。決策系統DS=(U，A，V，f)的任意兩個樣本都是同型樣本。

6)條件樣本：設(y，w1，w2，…，wm)是一向量，其中y是與論域U中數據同類型的數據，同時w1，w2，…，wm(m個)是與決策系統DS=(U，A，V，f)中任一樣本(x，u1，u2，…，um；v1，v2，…，vn)的條件函數值u1，u2，…，um(m個)類型和個數相同的值，此時稱(y，w1，w2，…，wm)為決策系統DS=(U，A，V，f)的條件樣本，簡稱條件樣本，y稱為條件樣本數據。顯然決策系統DS=(U，A，V，f)的樣本(x，u1，u2，…，um；v1，v2，…，vn)的子部分(x，u1，u2，…，um)是決策系統的條件樣本。

在表1的決策系統中，x1所在行對應的樣本是(x1，1，2；2，1)，其中x1是樣本數據，數值1，2是條件函數值，數值2，1是決策函數值，向量(x1，1，2)是條件樣本。

給定向量(y，u1，u2)，其中y是與論域U中數據同類型的數據，u1和u2是數值，此時(y，u1，u2)與表1中決策系統的每一條件樣本可能不同，但由于數值u1和u2的個數與樣本(x1，1，2；2，1)中條件函數值1，2的個數相同，所以(y，u1，u2)是表1中決策系統的條件樣本。

上述分析討論表明，決策系統DS=(U，A，V，f)不僅是集合U，A，V和信息函數f構成的數學結構，也可看做一系列同型樣本構成的結構體系。

1.2 基于樣本的決策

決策系統DS=(U，A，V，f)匯集了數據滿足條件和對應結論的信息，從條件到結論的對應就是決策的過程。如果從樣本的角度考慮，決策的過程是根據樣本的條件函數值，確定樣本數據的性質，并通過決策函數值予以反映。為了直觀，通過表1的決策系統進行討論。

考慮表1的決策系統DS=(U，A，V，f)，其各類信息可與實際問題聯系在一起，賦予它們具體的含義。設論域U={x1，x2，x3，x4，x5}中的數據表示5個學生，對于屬性集A={c1，c2}∪{d1，d2}，設定c1表示數學，c2表示語文，d1表示等級，d2表示獲獎。因此條件屬性c1和c2，以及決策屬性d1和d2可分別表示學生xi(i=1，2，3，4，5)在學校的數學和語文成績，以及由此確定的整體學習情況和獲獎信息，并通過條件函數值和決策函數值得到反映。表1中的條件函數值和決策函數值與數據xi之間的聯系如下：

如果c1(xi)=k，則表示學生xi的數學成績是第k等；

如果c2(xi)=k，則表示學生xi的語文成績是第k等；

如果d1(xi)=k，則表示學生xi的整體成績是第k級；

如果d2(xi)=1，則學生xi獲得獎勵，如果d2(xi)=0，則學生xi不獲得獎勵。

于是可對表1決策系統反映的學生信息進行如下分析。考慮x1所在的行，由于c1(x1)=1并且c2(x1)=2，所以學生x1的數學成績是第1等，語文成績是第2等，展示了x1滿足的條件。同時d1(x1)=2且d2(x1)=1，表明x1的整體成績是第2級，并且可以獲得獎勵，確定了對x1的評估結果。這表達了如此的信息：當學生x1的數學和語文成績一個是1等，一個是2等時，則該生的整體成績是2級，且可以得到獎勵。這樣的過程就是根據條件做出的決策，體現了學生x1數學和語文成績與評判結果之間的聯系。學生x2，x3，x4，x5的情況也可利用表1進行評判。

通過對表1各類信息與實際問題的聯系，可幫助對決策系統包含的決策信息進行理解。因此對于一般的決策系統DS=(U，A，V，f)，可依據上述直觀的解釋，對決策系統包含的決策信息給予描述，于是引出如下的概念。

7)設(y，w1，w2，…，wm)是決策系統DS=(U，A，V，f)的條件樣本，如果存在DS=(U，A，V，f)的樣本(x，u1，u2，…，um；v1，v2，…，vn)，使得w1，w2，…，wm分別與u1，u2，…，um對應相等，則稱條件樣本(y，w1，w2，…，wm)與樣本(x，u1，u2，…，um；v1，v2，…，vn)相匹配。

8)如果決策系統DS=(U，A，V，f)的條件樣本(y，w1，w2，…，wm)與決策系統DS=(U，A，V，f)的樣本(x，u1，u2，…，um；v1，v2，…，vn)相匹配，則稱決策函數值v1，v2，…，vn為條件樣本數據y的決策結論。

9)對于條件樣本(y，w1，w2，…，wm)，把獲得條件樣本數據y決策結論的過程稱為針對該條件樣本的決策。

所以決策系統DS=(U，A，V，f)中針對條件樣本的決策與相匹配的樣本密切相關。相匹配時，依據決策系統的決策將形成。不匹配時，則不能依據決策系統進行決策。

2 決策的分解處理

把一個決策系統作為參照模型，對于任意的條件樣本實施比對判定，如果在決策系統中存在與之相匹配的樣本，則該樣本的決策函數值作為條件樣本數據的決策結論，將確定該數據的性質，從而完成決策的過程。

2.1 決策的確定和不確定性

在一些情況下，對于給定的條件樣本，即使在決策系統中存在相匹配的樣本，但在確定條件樣本數據的決策結論時，可能遇到決策結論選擇上的不確定性。不妨通過表1的決策系統進行討論。

由表1可知，數據x3和x4分別對應樣本(x3，3，1；2，0)和(x4，3，1；3，0)，其條件函數值3，1相同，但決策函數值2，0和3，0不完全相同。于是對于表1決策系統的條件樣本(y，u1，u2)，如果(y，u1，u2)與(x3，3，1；2，0)相匹配，即數值u1，u2分別與3，1對應相等，則(y，u1，u2)與(x4，3，1；3，0)也相匹配。此時條件樣本數據y的決策結論遇到選擇2，0還是選擇3，0的問題，于是引入如下概念。

10)如果條件樣本數據的決策結論僅有唯一一組，則稱針對條件樣本的決策在DS=(U，A，V，f)中是確定的。

11)如果條件樣本數據的決策結論存在多組，則稱針對條件樣本的決策在DS=(U，A，V，f)中是不確定的。

決策的不確定性可通俗的表述為：相同的條件對應不同的結果。這在實際中也常常遇到，對此人們可通過思維分析，設法應對處理，不過也時常遭遇應對的困難。對于程序設計而言，當涉及決策的不確定性問題時，如果不能有效地應對處理，計算機則無所適從。

當決策系統涉及較多的屬性，特別決策屬性很多時，條件樣本數據的決策結論將涉及很多的決策函數值。因此如果能夠對眾多的決策屬性進行分解，分別考慮每一個決策屬性，使對較多決策函數值的考慮分解為對單一決策函數值的討論，由此對決策的確定或不確定性進行有效的判定，那么該分解方法對決策的確定與否具有清晰化的意義。下文將給出具體的方法，使判定得以分解處理。

2.2 決策的分解

考慮決策系統DS=(U，A，V，f)，其中A=C∪D及C∩D=?。下面的討論主要關注決策屬性，所以不妨設D={d1，d2，…，dn}。此時決策系統DS=(U，A，V，f)具有如下形式：

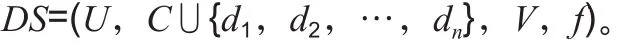
對于di∈{d1，d2，…，dn}(i=1，2，…，n)，構造決策系統如下：

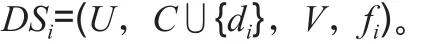
在決策系統DSi=(U，C∪{di}，V，fi)中，論域U、條件屬性集C和屬性值域V與決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)中的對應部分相同，而決策屬性集{di}中僅包含一個決策屬性di，此時DSi中的信息函數fi由DS中的信息函數f所確定：使當∈U×(C∪{di})時，滿足fi(x，a)=f(x，a)。實際上，fi是f在U×(C∪{di})上的限制，為了簡單仍用f表示fi。于是DSi=(U，C∪{di}，V，fi)=(U，C∪{di}，V，f)，并稱為決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)的子系統。

因此對于包含n個決策屬性的決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)，可以得到n個子系統：

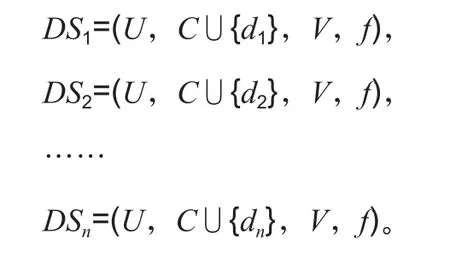
這n個子系統中的每一個僅包含一個決策屬性，形成了對決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)的分解。

由于決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)與其子系統DSi=(U，C∪{di}，V，f)(i=1，2，…，n)具有相同的條件屬性集C，所以如果(y，w1，w2，…，wm)是決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)的條件樣本，則(y，w1，w2，…，wm)也是子系統DSi=(U，C∪{di}，V，f)(i=1，2，…，n)的條件樣本。同時當(x，u1，u2，…，um；v1，v2，…，vn)是決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)的樣本時，向量(x，u1，u2，…，um；vi)(i=1，2，…，n)是子系統DSn=(U，C∪{di}，V，f)的樣本。

進而，當條件樣本(y，w1，w2，…，wm)與決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)的樣本(x，u1，u2，…，um；v1，v2，…，vn)相匹配時，該條件樣本(y，w1，w2，…，wm)與子系統DSi=(U，C∪{di}，V，f)的樣本(x，u1，u2，…，um；vi)(i=1，2，…，n)必然相匹配。

于是提出這樣的問題：在決策系統DS=(U，A，V，f)中，針對條件樣本(y，w1，w2，…，wm)的決策，與在子系統DSi=(U，C∪{di}，V，f)(i=1，2，…，n)中，針對條件樣本(y，w1，w2，…，wm)的決策具有怎樣的聯系？

結論1：針對條件樣本(y，w1，w2，…，wm)的決策在決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)中是確定的，當且僅當對于每一子系統DSi=(U，C∪{di}，V，f)(i=1，2，…，n)，針對(y，w1，w2，…，wm)的決策在DSi=(U，C∪{di}，V，f)中是確定的。

結論2：針對條件樣本(y，w1，w2，…，wm)的決策在決策系統DS=(U，C∪{d1，d2，…，dn}，V，f)中是不確定的，當且僅當存在一子系統DSi=(U，C∪{di}，V，f)(1≤i≤n)，使針對(y，w1，w2，…，wm)的決策在子系統DSi=(U，C∪{di}，V，f)中是不確定的。

鑒于篇幅，這里不給出這兩個結論的證明，僅通過表1的決策系統給予直觀的驗證。

由于表1中的決策系統包含兩個決策屬性，按照上述的分解方法，該決策系統DS=(U，C∪{d1，d2}，V，f)對應分解出兩個子系統DS1=(U，C∪{d1}，V，f)和DS2=(U，C∪{d2}，V，f)，它們都包含一個決策屬性，分別是d1和d2。這兩個子系統分別展示在表2和表3中。

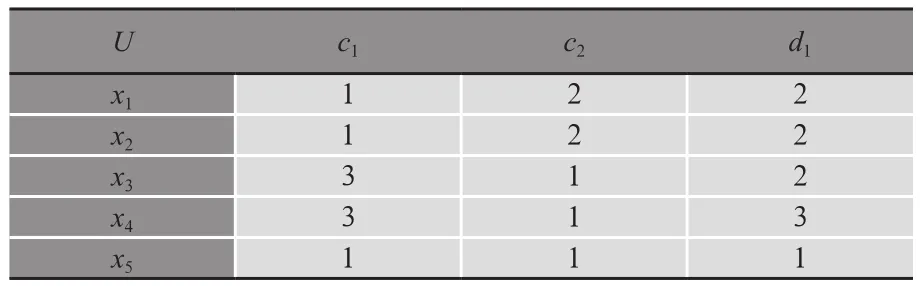
表2 子系統DS1

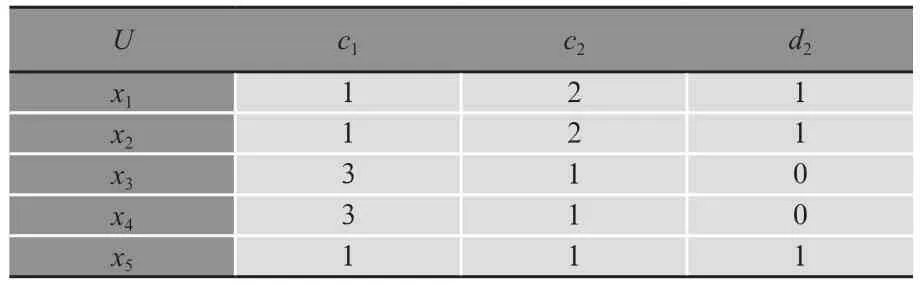
表3 子系統DS2

現考查條件樣本(y，1，2)。在表1的決策系統DS=(U，C∪{d1，d2}，V，f)中，條件樣本(y，1，2)與表1中的樣本(x1，1，2；2，1)和(x2，1，2；2，1)相匹配。由于樣本(x1，1，2；2，1)和(x2，1，2；2，1)的決策函數值都是2，1，所以條件樣本數據y的決策結論僅有唯一一組(即2，1)。因此針對條件樣本(y，1，2)的決策在表1的決策系統DS=(U，C∪{d1，d2}，V，f)中是確定的。另一方面，條件樣本(y，1，2)與表2子系統中的樣本(x1，1，2；2)和(x2，1，2；2)相匹配，此時條件樣本數據y的決策結論是2，唯一確定，因此針對條件樣本(y，1，2)的決策在表2的子系統DS1=(U，C∪{d1}，V，f)中是確定的。同樣，條件樣本(y，1，2)與表3子系統中的樣本(x1，1，2；1)和(x2，1，2；1)相匹配，此時條件樣本數據y的決策結論是1，也唯一確定，因此針對條件樣本(y，1，2)的決策在表3的子系統DS2=(U，C∪{d2}，V，f)中也是確定的。于是針對條件樣本(y，1，2)的決策在決策系統DS=(U，C∪{d1，d2}，V，f)中的確定性與在子系統DS1=(U，C∪{d1}，V，f)和DS2=(U，C∪{d2}，V，f)中的確定性是相同的，這是對結論1的驗證。

再考慮條件樣本(y，3，1)，它與表2子系統DS1=(U，C∪{d1}，V，f)中的樣本(x3，3，1；2)和(x4，3，1；3)相匹配，此時條件樣本數據y的決策結論涉及兩組，分別是2和3，因此針對條件樣本(y，3，1)的決策在子系統DS1=(U，C∪{d1}，V，f)中是不確定的。另一方面，條件樣本(y，3，1)與表1決策系統DS=(U，C∪{d1，d2}，V，f)中的樣本(x3，3，1；2，0)和(x4，3，1；3，0)相匹配，此時條件樣本數據y的決策結論涉及兩組，分別是2，0和3，0，因此針對條件樣本(y，3，1)的決策在決策系統DS=(U，C∪{d1，d2}，V，f)中是不確定的。該討論表明，針對條件樣本(y，3，1)的決策在子系統DS1=(U，C∪{d1}，V，f)中不確定時，在原決策系統DS=(U，C∪{d1，d2}，V，f)中也是不確定的，這是對結論2的驗證。

結論1和結論2表明，在決策系統中針對條件樣本決策的確定或不確定判定可等價轉換到僅包含一個決策屬性的子系統中。這種對決策系統的分解處理是其他討論不曾涉及的方法，達到了清晰或簡化判定過程的目的。

在應用方面，文獻[14]、[15]的討論把醫學診斷基于數據決策的判定，并與決策屬性的分解存在聯系。

3 結語

把決策系統分解為一系列僅包含一個決策屬性的子系統，將決策系統中針對條件樣本的決策等價地轉換到子系統中，是本文建立的方法。由此使以決策函數值為判定依據的決策得到了清晰的判定，實現了決策問題分解處理的目的。特別地，當針對條件樣本的決策在決策系統中具有不確定性時，由結論2，可通過在一子系統中針對條件樣本決策的不確定判定得以完成，這顯然簡化了判定的過程。

把決策系統作為決策問題判定的參照模型，對條件樣本實施比對判定，得到決策結論，形成確定或不確定決策信息的過程體現了機器學習的數據處理思想，同時也有別于傳統的機器學習算法。這基于作者對決策問題與機器學習方法的理解，展示了求變的思想。決策的分解處理為決策問題的清晰簡化提供了路徑，是判定方法的核心。

[1]閆林.數理邏輯基礎與粒計算[M].北京:科學出版社,2007

[2]Wang C Z,He Q,Chen D G.A novel method for attribute reduction of covering decision system[J].Information Sciences,2014(254):181-196

[3]Jia X Y,Liao W H,Tang Z M.Minimum cost attribute reduction in decision-theoretic rough set models[J].Information Sciences,2013(219):151-167

[4]Yan L,Yan S.Granular computing and attribute reduction based on a new discernibility function[J].International Journal of Simulation: Systems,Science and Technology,2016,17(33):24.1-24.10

[5]McAllister R A,Angryk R A.Abstracting for dimensionality reduction in text classification[J].International Journal ofintelligent Systems,2013,28(2):115-138

[6]閆碩,閆林.數據關聯的粒化樹描述方法[J].模式識別與人工智能,2015,28(12):1057-1066

[7]Tagarelli A.Exploring dictionary-based semantic relatedness in labeled tree data[J].Information Sciences,2013,220:244-268

[8]Yan S,Yan L,Wu J Z.Rough data-deduction based on the upper approximation[J].Information Sciences,2016,373:308-320

[9]Yan L,Yan S.Granular reasoning and decision system's decomposition[J].Journal of Software,2012,7(3):683-690

[10]She Y H.On the rough consistency measures of logic theories and approximate reasoning in rough logic[J].International Journal of Approximate Reasoning,2014,55(1):486-499

[11]閆林,高偉,閆碩.數據合并的結構粒化方法與矩陣計算[J].計算機科學,2017,44(9):261-265

[12]Min F,Hu Q H,Zhu W.Feature selection with test cost constraint[J].International Journal of Approximate Reasoning,2014,55(1):167-179

[13]Ma W J,Xiong W,Luo X D.A model for decision making with missing,imprecise,and uncertain evaluations of multiple criteria[J].International Journal ofintelligent Systems,2013,28(2):152-184

[14]Yao J T,Azam N.Web-based medical decision support systems for three-way medical decision making with game-theoretic rough sets[J].IEEE Transactions on Fuzzy Systems,2015,23:3–15

[15]Pauker S G,Kassirer J P.The threshold approach to clinical decision making[J].New England Journal Medicine,1980,302:1109–1117