灰色關聯分析的備件分類方法*

曾翔，徐廷學，安進，顧鈞元

(海軍航空工程學院 兵器科學與技術系，山東 煙臺 264001)

0 引言

在當今社會，為使工廠企業日常的生產運營得到有效保證，其中重要的一個環節即是對備件精準高效地庫存配置。而備件分類作為一種重要的庫存控制手段，它直接決定了庫存管理水平的高低，是實現備件庫存保障的基礎和前提。因此，根據不同行業的庫存保障要求，結合影響其備件分類的不同因素，研究相應的備件分類算法是十分重要的。

一直以來對于備件的分類管理都備受關注。備件分類理論始于1951年的ABC分類法，并且其所遵循的帕累托準則成為后來絕大多數備件分類改進方法的基礎原則。1983年卡拉杰克(Kraljic)針對這一問題首次提出基于Kraljic矩陣的二維分類方法[1]。在國內徐寶強提出備件庫存的“3A”分類法[2]。徐曉燕提出基于需求預測的備件分類法[3]。崔南方等提出了基于數據包絡分析(data envelopment analysis，DEA)的備件分類方法[4]。張作剛[5]、姜晨[6]等分別運用支持向量機原理及其改進方法對備件進行ABC分類。但這些分類方法所運用的理論都較為單一，隨著研究的深入，Braglia[7]，崔南方[8]等通過分析影響備件分類的各因素，應用層次分析法(analytic hierarchy process，AHP)對備件進行多準則分類，受此啟發，以AHP分類為基礎，結合模糊評判原理[9-11]、灰色分析理論[12]、VED(vital essential desirable)分類[13]等的研究相繼開展，極大豐富了備件分類方法。

這些方法在分類準則的選擇上主要可分為2個方面，即僅只考慮客觀數據的分類方法，典型如基于DEA原則的分類；和引入專家經驗的主觀分類方法，典型如基于AHP原則的方法。但是，盡管DEA不考慮指標權重且不受量綱影響，但這些分類指標在被生硬劃分為輸入和輸出2類時，各自間聯系不大，不能完美體現分類的優勢，且完全忽視決策者本身的經驗及影響，這是不妥當的。另一方面，AHP在將專家的主觀判斷過程進行量化時，在對作出這一判斷的專家選擇上有時會顯得說服力不強[14-15]。例如從事維修的專家和從事庫存管理專家，二者對何謂“重要”備件的看法上是有差別的，維修專家認為那些失效會給工廠帶來嚴重后果的備件是重要備件。而庫存管理專家選擇重要備件會更加看重諸如庫存成本、供應商數量等相關因素。

在這樣的一個矛盾中，本文提出一種結合IGAHP(improved group AHP，IGAHP)，SE-DEA以及灰色關聯理論的備件分類方法，綜合3種理論各自的優點，通過IGAHP引入多位專家意見減少單一專家在AHP中的主觀偏差，以SE-DEA和IGAHP共同確定分類指標權重，并最終以灰色關聯分析為橋梁綜合二者分析的結果，計算出最終備件分類的結果。

1 基于IGAHP和SE-DEA的備件分類方法

1.1 改進群體層次分析法(IGAHP)

層次分析法通過對定性、定量準則的賦值，結合不同層次的權重向量解決多屬性決策問題。AHP把數學處理與人的經驗等相結合，通過綜合專家的判斷有效分析各準則間的關系。但在實際應用中，其也存在如下不足：一是因不能集結多位專家的意見而存在單個專家判斷上的偏差；二是在構造判別矩陣時缺乏彈性，無法表達判別的模糊性；三是一旦一致性檢驗的結果顯示不一致時，所得權重向量的可信度會大大降低。

本文提出的改進群體層次分析法的基本思路是通過每位專家確定的判別矩陣，求出各自的權重，再通過分析判斷其差異程度確定權重系數，最后運用所得的各權重系數對各專家權重進行集結，得到指標集的最終權重判斷。具體過程如下：

(1) 構造判斷矩陣

使用1～9的比例標度作為賦予相對重要度大小的數值作為判斷矩陣。假定B層指標中的指標Bs包含下一層次C中的指標C1,C2,…,Cn。aij(i=1,2,…,n;j=1,2,…,n)表示C層指標中的Ci與Cj相比的相對重要性標度值。則aij滿足：

(1)

通常參與指標權重分配的專家有多個，由于各專家的知識、經驗上的差異，其決策權重系數也應不同，因此，需合理確定各專家的決策權重系數。

(2) 計算每位專家評定的指標權重

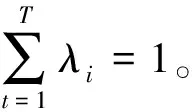
(2)

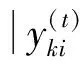
3) 識別判別矩陣中的異常元素并加以調整

由于可能會出現C.R.(t)>0.1的現象，需對判斷矩陣進行調整。考慮到其中判斷元素的錯誤只是個別的，不會出現大面積錯誤。基于此進行調整。調整方法為：

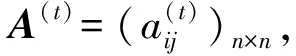
(3)

令k=1,2,3,…，并設k=1時，則A(t)(k)=A(t)，Y(t)(k)=Y(t)。

b.構造錯誤元素識別矩陣

(4)

c.令

(5)

(6)

d.令

(7)

(4) 各專家的決策權重系數確定模型

設第p個專家與第q個專家決策的相近程度用距離dpq(p,q=1,2,…,T)表示，則

(8)

dpq滿足：①dtt=0；②dpq=dqp≥0；③dpq越小，表明2位專家的判斷越接近。當且僅當dpq=0且p≠q時，說明這2位專家的判斷完全一致。

設第t個專家決策與其他所有專家決策的相似程度用dt表示，則

(9)

式中：j=1,2,…,T。可知，dt≥0，dt越小表示Y(t)與其他特征向量越接近，當dt=0時，dt1=dt2=…=dtT=0，說明所有特征向量都相等，每一位專家的判斷都一樣。

綜上，第t位專家的最終決策權重系數λt為

當dt=0時

(10)

當dt≠0時，

(11)

式中:j=1,2,…,T，可知，當dt越大時，表明該專家與其他專家之間的分歧越大，其決策權重系數越小；反之亦然。

(5) 指標權重集結

(12)

1.2 超效率數據包絡分析法(SE-DEA)

DEA模型是利用輸入、輸出數據建立適合每個決策單元線性規劃的一種數學模型，通過計算得到該線性規劃的最優解，并將之作為效率值來評價決策單元的有效性，這其中最為常用的即是C2R模型，但該模型在實際應用中往往會出現因效率值相同而無法進行比較排序的問題，這在備件分類中是不合適的，為此，本文采用可有效排序的SE-DEA模型，其模型表達式如下：

(13)

式中:X,Y為輸入和輸出指標；θ為最終求得的超效率值；s-為剩余變量，即輸入指標權重向量；s+為松弛變量，即輸出指標權重向量，矩陣[s-,s+]即指標權重矩陣，并且利用線性比例法對其作歸一化處理。

1.3 計算綜合權重

利用線性加權方法確定最終的綜合指標權重，具體公式為

(14)

1.4 基于IGAHP和DEA的灰色關聯分析模型

(1) 設待分類備件數量為m，分類指標數為n，則由備件及其各自指標構成的分析模型矩陣為

(15)

(2) 確定備件分類最優指標集D0。當評價指標是成本性指標時，表示其值越小越好，則最優值為所有對應具體值中的最小值，反之，當為效益型指標值時，其最優值為所有對應具體值中的最大值。最優集確定后，構造矩陣為

(16)

(3) 考慮到指標量綱和數量級的差異，需對矩陣G進行規范化處理，這里采用Z-score方法，設G中第i列元素的均值和標準差為μi及σi，則G中某元素dji經規范后為

(17)

(4) 確定關聯系數矩陣

依灰色關聯分析原理得第m個備件的第n個指標與最優指標間的關聯系數

(18)

式中：ρ為分辨系數，且ρ∈[0,1]，本文設定為0.5，于是可得灰色關聯系數矩陣為

(19)

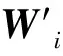
(20)

1.5 基于灰色關聯分析的備件分類方法

1.5.1 備件分類指標體系

通過對各備件分類方法的分析，本文總結歸納出如下6個備件分類指標：

(1) 消耗金額。即備件的年消耗總花費，表示備件單價與備件年平均消耗量的的乘積。

(2) 缺貨損失。即因備件缺貨導致企業生產、管理等方面的損失。

(3) 供應商數量。即市場上提供相應備件的生產銷售廠商。

(4) 庫存費用。即妥善存儲備件所產生的相應維護費用。

(5) 訂貨提前期。即采購備件從訂貨開始到最終入庫存儲所需時間。

(6) 關鍵系數。即備件所屬設備及其所屬零部件對企業生產影響程度大小的表征。

1.5.2 基于灰色關聯分析的備件分類方法

結合前述分析，本文所提的分類方法流程圖如圖1所示。具體過程按圖中順序標注可簡述為：

(1) 利用構建的指標體系，通過咨詢該領域的多位專家，分別給出上述6個指標的AHP判斷矩陣，并利用所提IGAHP方法計算出引入決策者經驗的綜合評價向量W1。

(2) 將關鍵系數和供應商數量作為輸入指標，其他4類指標作為輸出指標，利用SE-DEA計算出客觀評判下的綜合評價向量W2i；并利用線性加權結合W1得到各指標的最終權重Wi。

(3) 分析實際待分類各備件的指標數據，構建分析矩陣D，利用式(15)～(17)得到由最優指標集與各備件數據共同構成的規范矩陣G。

(4) 根據式(18)計算出原始的各備件與最優集間的灰色關聯系數矩陣E，最終通過式(20)結合各指標權重Wi得到最終灰色關聯度Ri，并由大到小進行排序，依據帕累托分類原理，依次將關聯度值數量占總數量20%的備件劃歸為A類備件，占總數量30%的備件劃歸為B類備件，占總數量50%的備件劃歸為C類備件。

2 仿真校驗

對某型裝備中的備件作抽樣分析，選出其中30種備件的分類指標體系數據如表1所示，并按本文所提方法流程進行仿真校驗。

表1備件分類指標樣本

Table1Indexsamplesofsparepartsclassification

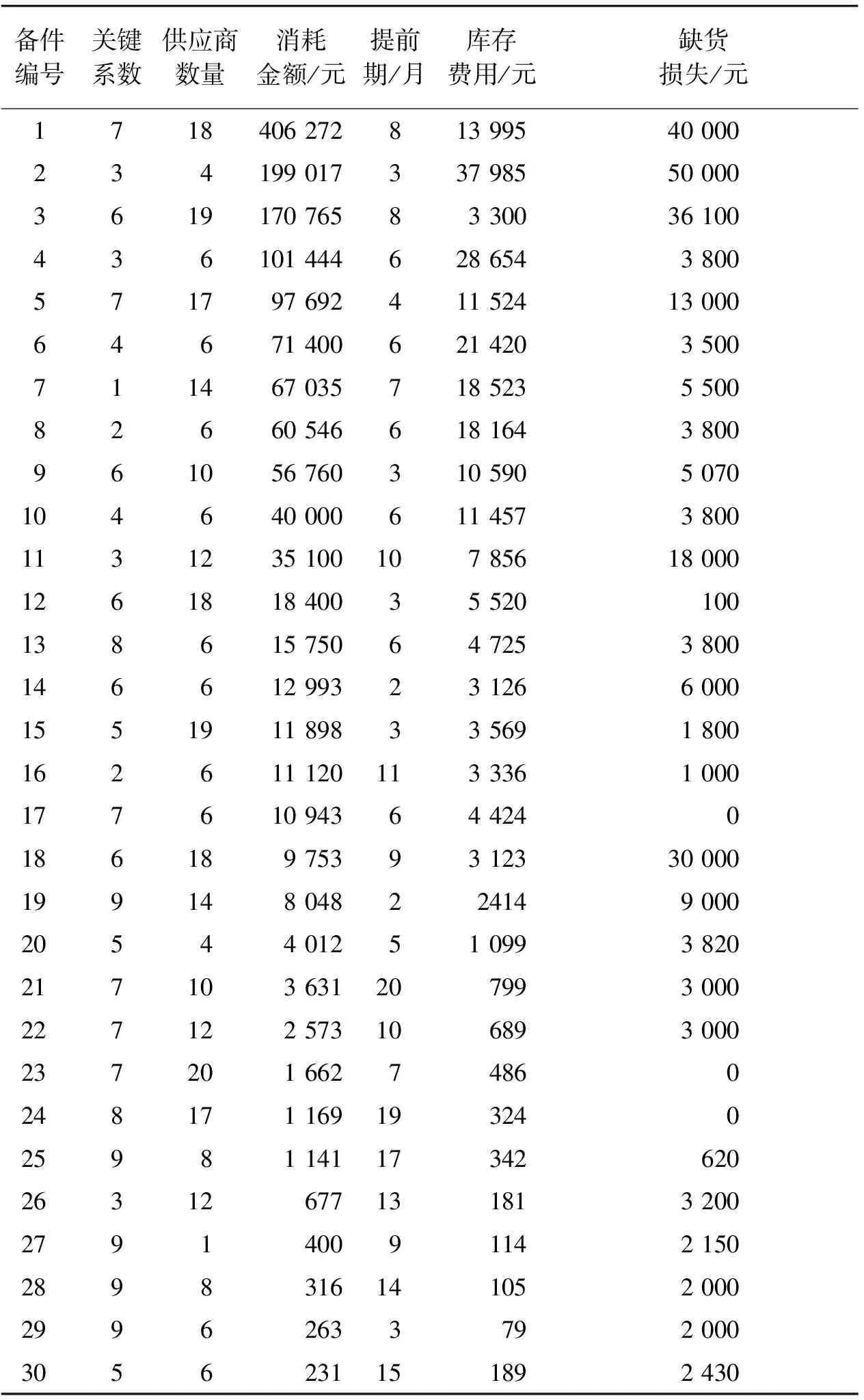
備件編號關鍵系數供應商數量消耗金額/元提前期/月庫存費用/元缺貨損失/元171840627281399540000234199017337985500003619170765833003610043610144462865438005717976924115241300064671400621420350071146703571852355008266054661816438009610567603105905070104640000611457380011312351001078561800012618184003552010013861575064725380014661299323126600015519118983356918001626111201133361000177610943644240186189753931233000019914804822414900020544012510993820217103631207993000227122573106893000237201662748602481711691932402598114117342620263126771318132002791400911421502898316141052000299626337920003056231151892430

(1) 依1.5.2節中所述第1步流程，分別咨詢3位專家給出AHP的判斷矩陣，如表2所示。

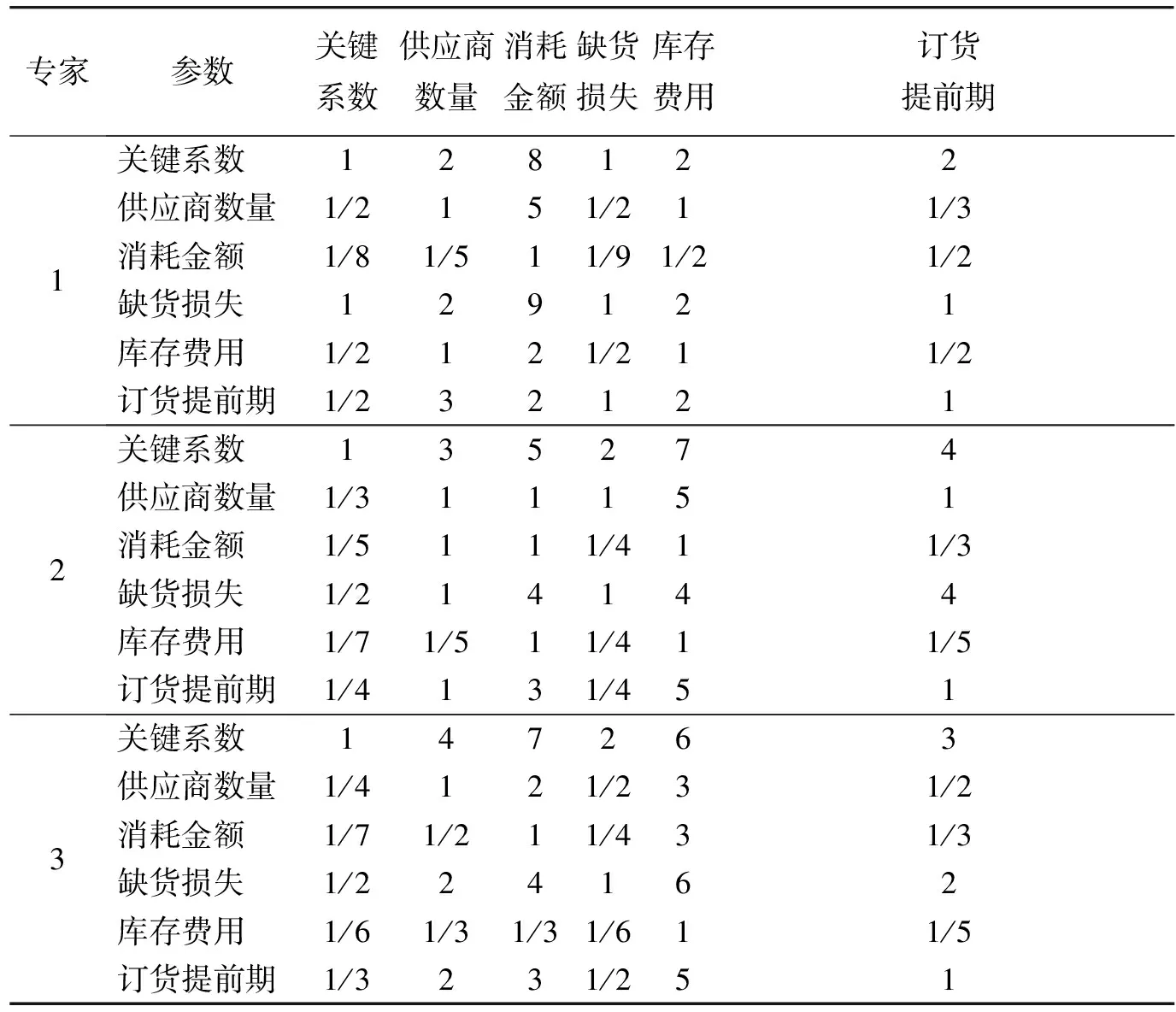
表2 IGAHP判斷矩陣

2) 由式(9)確定各專家的決策權重系數d12=0.152 2，d13=0.144 3，d23=0.038 7，則d1=0.296 5，d2=0.190 8，d3=0.183 0，由式(12)得到各專家的決策權重系數，λ1=0.239 6，λ2=0.372 2，λ3=0.388 2。

3) 指標權重的集結

代入各專家的決策權重系數和特征向量，由式(13)得到該組指標的最終權重向量Y*=(0.367 4，0.139 7，0.058 9，0.238 6，0.056 9，0.155 9)。

(2) 依1.5.2節中所述第2步流程，其所得最終結果如表3中的方法2所得數據，并將其作為評判本方法的優劣加入最終分類對比中。

(3) 依1.5.2節中所述第3,4步流程，本文所提SE-DEA與IGAHP結合的備件分類方法的最終結果如表3中的方法4所示。另外，除將方法2加入最終結果對比外，將利用傳統ABC分類法(方法1，表1中備件編號即是按照方法1順序列出，故不列于表2中)、單一的AHP與SE-DEA結合方法(方法3，僅選用專家1給出的判斷矩陣)計算所得結果也加入對比，綜合驗證本文所提方法的效果，結果如表3所示。

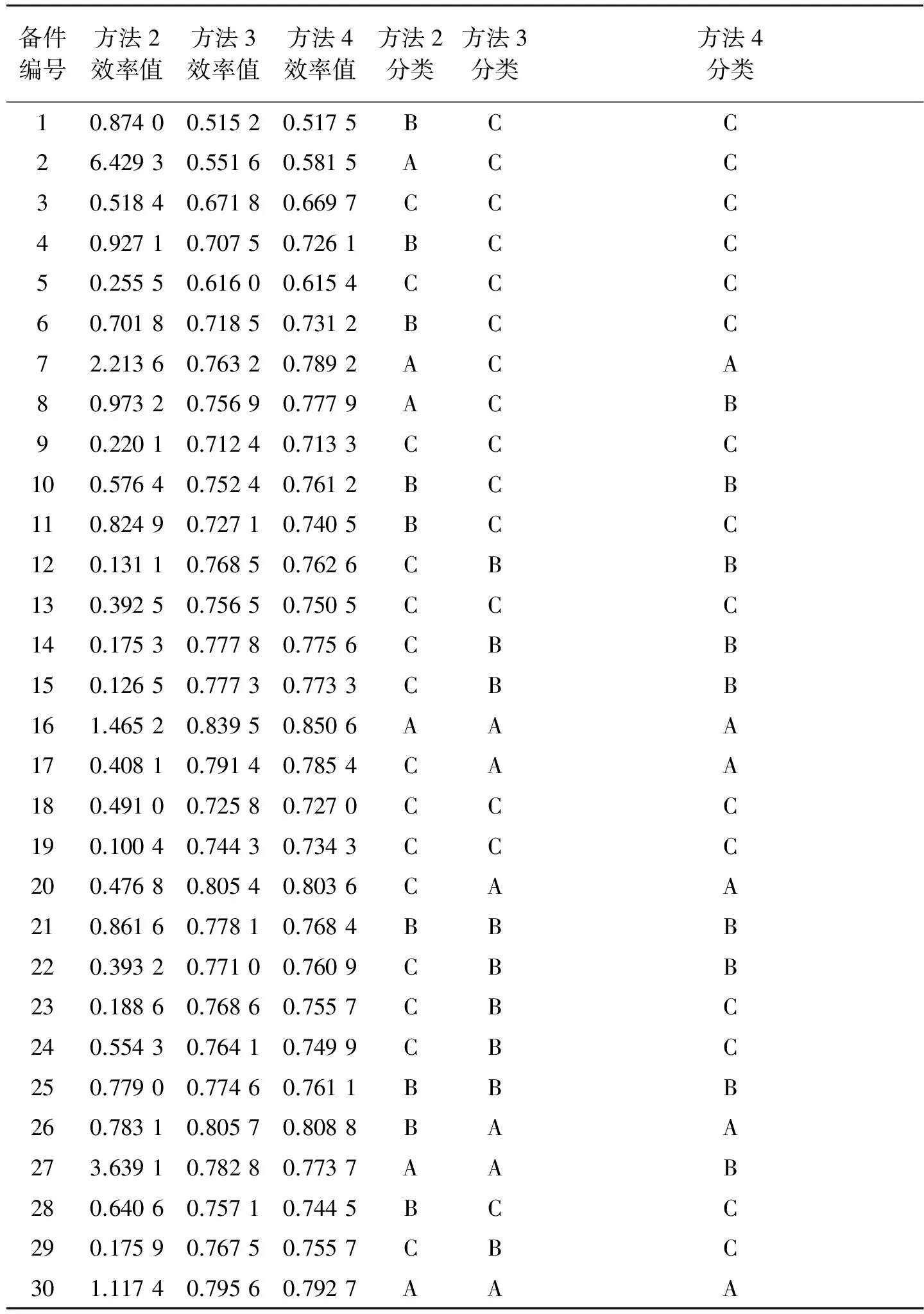
表3 各方法分類結果

通過表1，3可知，4種方法在某些備件的分類上會出現不同的結果，例如備件29，方法1，2，4都判斷其為C類件，但方法3判斷其為B類件，參考其本身指標，不難發現，其各項指標在整個樣本中都是較為靠后的，并沒有值得關注的數值，故將其放在C類件是合適的，造成這一結果的原因即是單個專家判斷矩陣上的主觀影響；又如備件20，方法3，4都將之歸為A類件，方法1，2歸為C類件，觀察其指標，其供應商數量、關鍵系數及訂貨提前期都較為靠前，而這3個指標在最終的權重向量中的占比都很重，故應將其歸為A類件，過于強調客觀結果而忽視決策者的經驗往往就會導致這種情況的出現。通過這些對比結果說明，本文方法綜合了備件主觀分類與客觀分類法的優點，在主觀容錯性能上具有較強的優勢，因此其分類結果也更為合理。

3 結束語

本文提出了一種基于灰色關聯分析的備件分類方法，將現有備件分類方法中的以AHP分類為代表的主觀分類法與以DEA分類為代表的客觀分類法相結合，并通過IGAHP彌補了單個專家經驗對AHP分類中的主觀影響，以SE-DEA解決可能出現的效率值相同而無法排序的問題，并通過灰色關聯分析將二者結合，一方面使得DEA分類不能引入決策者經驗的問題得到解決，另一方面提高了AHP分析的主觀容錯性。最后實例分析的結果表明,本文備件方法更為準確、合理，能夠為相關領域的研究提供有益的參考。

參考文獻：

[1] BANKS J,FABRYCKY W J.Procurement and Inventory Systems Analysis[M].Englewood Cliffs,New Jersey:Prentice-Hall,1987.

[2] 徐寶強，李葆文，魏昕.從備件ABC分類管理到備件3A庫存模型應用[J].設備管理與維修，2007(9)：10-11.

XU Bao-qiang，LI Bao-wen，WEI Xin.From ABC Classifying Method of Spare Part to Application of 3A Inventory Model[J].Plant Maintenance Engineering，2007(9)：10-11.

[3] 徐曉燕.一種基于需求特性分類的備件庫存管理方法及其實證研究[J].系統工程理論與實踐，2006(2)：62-67．

XU Xiao-yan.A Demand Classification Based Approach of Inventory Management for Spare-Parts and Its Application[J].Systems Engineering-Theory & Practice，2006(2)：62-67.

[4] 崔南方，魯家晶.基于DEA的備件ABC分類模型[J].物流技術,2007,26(3):55-58．

CUI Nan-fang，LU Jia-jing.ABC Classification Model for Spare Parts Based on DEA[J].Logistics Technology,2007,26(3):55-58.

[5] 張作剛，劉星，彭作鵬，等.基于支持向量機的多準則航材ABC分類法[J].價值工程，2010，29(22)：248-249.

ZHANG Zuo-gang，LIU Xing，PENG Zuo-peng，et al.Based on Support Vector Machine Multi-Criteria ABC Classification of Aerial Material[J].Value Engineering，2010，29(22)：248-249.

[6] 姜晨，徐廷學，余仁波.基于DAGSVM的裝備不常用備件分類方法[J].艦船科學技術，2011，33(7)：135-139.

JIANG Chen，XU Ting-xue，YU Ren-bo.Classified Method Equipment Rarely Used Spare Parts Based on DAGSVM[J].Ship Science and Technology，2011，33(7)：135-139.

[7] BRAGLIA M，GRASSI A， MONTANARI R.Multi-Attribute Classification Method for Spare Parts Inventory Management[J].Journal of Quality in Maintenance Engineering，2004，10(1)：55-65.

[8] 崔南方，羅雪.維修備件基于AHP的ABC分類模型[J].工業工程與管理，2004(4)：33-36.

CUI Nan-fang，LUO Xue.ABC Classfication Based on AHP in Servicing Spare Part[J].Industrial Engineering and Management，2004(4)：33-36.

[10] 張仲敏，李俊山，嚴其飛，等.電子對抗裝備維修備件混合分類決策模型[J].火力與指揮控制，2014，39(4)：58-62，67.

ZHANG Zhong-min，LI Jun-shan，YAN Qi-fei，et al.A Hybrid Decision Approach for Classification of ECM Equipment Spares[J].Fire Control & Command Control，2014，39(4)：58-62，67.

[11] 馬應欣，張作剛.基于AHP和模糊方法的庫存航材ABC分類模型[J].物流技術，2008，27(2)：130-133.

MA Ying-xin，ZHANG Zuo-gang.ABC Classification Model of Aircraft Spares Based on AHP and Fuzzy Evaluation[J].Logistics Technology，2008，27(2)：130-133.

[12] 孔琳，陳鴻宇，曾斌.基于AHP和灰色分析法的備件ABC分類模型[J].艦船電子工程，2008，28(1)：90-93.

KONG Lin，CHEN Hong-yu，ZENG Bin.ABC Classification for Spare Parts Based on AHP and Grey Analysis Process[J].Ship Electronic Engineering，2008，28(1)：90-93.

[13] MOLENAERS A， BAETS H， PINTELON L，et al.Criticality Classification of Spare Parts：A Case Study[J].Int.J.Production Economics，2012，140：570-578.

[14] 陳奎，韋曉廣，牛俊萍，等.基于AHP-DEA模型的電網規劃方案綜合評判決策[J].電力系統保護與控制，2014，42(21)：40-46.

CHEN Kui，WEI Xiao-guang，NIU Jun-ping，et al.Comprehensive Judgment for Power System Planning Alternatives Based on AHP-DEA[J].Power System Protection and Control，2014，42(21)：40-46.

[15] 王先甲，張熠.基于AHP和DEA的非均一化灰色關聯方法[J].系統工程理論與實踐，2011，31(7)：1222-1229.

WANG Xian-jia，ZHANG Yi.Non-Uniform Grey Relational Method Based on AHP and DEA[J].Systems Engineering-Theory & Practice，2011，31(7)：1222-1229.