共軸雙旋翼直升機扭振系統固有特性計算方法研究

劉永志 查建平

摘要：區別于常規單旋翼帶尾槳直升機，共軸雙旋翼直升機具有獨特的動力傳動構型，其所構成的扭振系統特性也具有自身特點。采用模態綜合法分析建立此類直升機的扭振系統動力學分析模型，通過算例對該系統扭振固有特性進行了計算和結果分析，驗證了此種分析計算方法的可行性。結果表明，此方法可用于研究共軸雙旋翼直升機扭振系統固有特性，同時該方法可在共軸雙旋翼直升機初步工程設計階段為旋翼及動力傳動系統的設計提供一定的設計指導。

關鍵詞：共軸雙旋翼；直升機；扭振；固有特性；計算方法

中圖分類號：V215.9

文獻標志碼：A

DOI：10.19452/j.issn1007-5453.2018.01.021

直升機扭振系統是指由旋翼、尾槳、動力傳動系統和發動機組成的機械扭振系統，該系統在直升機飛行及地面開車時會受到基頻為轉速Ω的N倍（N為槳葉片數）的交變扭矩的作用。當直升機扭振系統的固有頻率與激勵頻率相接近以至重合時，扭振系統就會產生過大的交變載荷，以致引起結構的提前疲勞破壞，同時也會引起直升機較大的振動。在國內外直升機研制過程中，出現扭振系統動力學問題的典型案例有延安二號、SA330、SA365N1、S-76、“虎”型直升機等。

當前，包括主旋翼在內的直升機扭振系統的固有特性可通過商用軟件或自編程的方法計算得到。相比傳統構型的直升機，共軸雙旋翼直升機的動力傳動系統的設計具有自身的特點：該類直升機具有繞同一理論軸線一正一反旋轉的上下兩幅旋翼，由于轉向相反，兩副旋翼產生的扭矩在航向不變的飛行狀態下相互平衡，因此，該類直升機不需要尾槳平衡反扭矩。俄羅斯卡莫夫設計局的共軸雙旋翼直升機設計技術最為成熟，其設計的卡-28、卡-50等直升機均性能優異，不過國內相關技術資料比較少，而我國在扭振系統方面的研究大多集中在傳統單旋翼帶尾槳直升機上，對于此類共軸雙旋翼直升機的研究開展較少。

基于此，本文以共軸雙旋翼直升機的扭振系統作為研究對象，利用模態綜合法建立該系統的動力學分析模型，對典型狀態下扭振系統固有特性進行了算例計算，論證了此種方法的可行性，同時為今后我國開展共軸雙旋翼直升機扭振系統的工程研制提供理論支持。

1旋翼擺振集合型固有特性計算模型

由于旋翼有多片槳葉，可形成集合型和周期型擺振，而周期型又分為前進型和后退型。其中，只有旋翼集合型與傳動系統扭振耦合，所謂集合型擺振是所有槳葉擺振幅值和相位都相同。計算旋翼擺振固有特性通常采用有限元法建立槳葉擺振動力學方程，用式（1）表示，根據邊界條件處理好邊界約束，從而確定了所考慮的旋翼運轉狀態下擺振固有特性。式中：[Mr]為槳葉質量矩陣，[Crl為槳葉阻尼矩陣，主要包括了氣動力阻尼、結構阻尼以及減擺器阻尼，[Kr]為槳葉剛度矩陣。式（1）中阻尼矩陣不是對稱矩陣，僅在進行扭振系統穩定性計算中使用，不用于進行槳葉擺振模態特性的計算。采用一般特征值求解方法解槳葉擺振方程，可得到槳葉各階擺振固有頻率和振型。

當通過求解式（1）得到槳葉的擺振振型矩陣[XM]后，進行模態變換，則方程變為所關注的擺振模態坐標下的槳葉擺振模態方程：式中：ζp為槳葉模態坐標，[Mp]為槳葉模態質量矩陣，[Cp]為槳葉模態阻尼矩陣，[Kp]為槳葉模態剛度矩陣，其模態變換表達式為：

2動力傳動系統動力學分析模型

動力傳動系統扭振方程可表示為：式中：[It]為動力傳動系統質量矩陣，[Ct]為動力傳動系統阻尼矩陣，[Kt]為動力傳動系統剛度矩陣。采用一般特征值求解方法，得到動力傳動系統扭振固有頻率和振型。當考慮的節點較多時，解得的模態頻率個數也多。一般動力傳動系統的有限元模型建模依據結構設計提供的參數和設計圖進行，為了較準確地預測扭振固有頻率，需要較細的設計數據和圖紙，這樣有利于開展參數敏感性分析，對于頻率設計調整更能找到突破點。非耦合狀態下的動力傳動系統扭振頻率和振型分析，既可以了解系統本身的設計和設計變化對頻率和振型的影響，更是分析耦合對動力傳動系統頻率和振型影響的依據。

把式（4）變換成模態坐標下的模態方程：式中：θq為傳動系統模態坐標，[Iq]為動力傳動系統模態質量矩陣，[Cq]為動力傳動系統模態阻尼矩陣，[Kq]為動力傳動系統模態剛度矩陣，令[QM]為模態振型矩陣，則其模態變換表達式為：

3旋翼動力傳動系統耦合扭振系統分析模型

由于旋翼與動力傳動系統耦合，需要考慮的僅是旋翼擺振集合型模態，因此，將槳葉擺振模態參數乘以槳葉片數即為旋翼集合型擺振模態參數。旋翼擺振運動是在旋轉坐標系中描述，其擺振模態與動力傳動系統扭振模態只存在慣性耦合，設槳轂處旋翼軸的扭轉變形為θH，槳葉的擺振位移坐標變量V=φ（r）·θH+XM·ζ，φ（r）是槳葉在槳轂處的約束振型，r是槳葉的展向坐標，對式（1）中的質量和阻尼矩陣進行變換，可得到旋翼動力傳動系統子結構在界面處質量和阻尼耦合矩陣。再按照傳動系統子結構的模態變換關系把θH用模態坐標θq表示，同時計算扭振固有特性時，阻尼項和右端項置0，最后得到旋翼動力傳動耦合扭振系統綜合模態方程：式中：Ir為槳葉展向位置r處的槳葉剖面模態質量。聯立求解上述方程可得到整個耦合全部固有頻率和振型。同時，可了解和研究耦合狀態下旋翼的集合型擺振頻率變化，同樣也可分析動力傳動系統固有頻率和振型的變化情況。

4算例

以典型共軸雙旋翼直升機為例，對該種直升機扭振系統的扭振固有特性進行計算，通過對比耦合前后的計算結果得到此類直升機扭振系統特性的相關規律。

4.1旋翼擺振模態計算

為得到旋翼擺振集合型模態參數，首先計算孤立槳葉擺振前三階擺振模態頻率、模態振型矢量，槳葉以鉸接形式連接槳轂支臂，擺振鉸位置在槳葉0.13R（R為槳葉半徑）處，采用有限元法，將槳葉進行分段處理，利用各段結構參數，計算旋翼100%轉速、100%升力條件下單片槳葉振型圖，如圖1所示。

本算例中槳葉旋轉角頻率為Ω=50rad/s，計算過程中對計算參數進行無量剛化處理，得到槳葉模態質量、模態剛度計算結果如下：

對得到的模態參數進行計算，并恢復槳葉擺振頻率的量綱（即根據矩陣Mp，Kp得到的頻率結果需乘以槳葉旋轉角頻率倍數），計算得到槳葉前三階擺振頻率為3.29Hz、29.87Hz、81.97Hz。

4.2動力傳動系統固有特性計算

動力傳動系統是指不包括旋翼在內的結構，其動力學分析模型的簡化遵循以下原則：

（1）傳動系統由只有轉動慣量的節點和只有扭轉剛度的扭元組成，齒輪簡化成只有轉動慣量的節點，其中齒輪的剛度合并到所連軸剛度中，軸簡化成只有扭轉剛度的扭元，將其轉動慣量平均分到兩端所連節點上，發動機節點主要指發動機動力渦輪部分，并考慮動力軸的轉動慣量。

（2）實際的直升機動力傳動系統中，由于存在多個減速器使整個系統各軸段的轉速不一致，按照能量等效原理，將實際剛度和轉動慣量轉換為對于旋翼參考轉速NRef下的當量剛度和當量轉動慣量。

圖2是兩臺發動機的共軸雙旋翼直升機動力傳動系統扭振特性分析模型，相比于普通的單旋翼帶尾槳直升機，共軸雙旋翼直升機在主減速器齒輪的布置上存在其特殊性，因此，計算時將主減速器內部分為三部分：主減速器共用部分、上旋翼減速齒輪和下旋翼減速齒輪，分別作為獨立的計算節點進行計算。圖2中，線段代表傳動軸，圖中相應標出了轉動慣量和剛度的符號，IUMH表示上旋翼槳轂的轉動慣量，KUMR表示上旋翼槳轂和上旋翼減速齒輪之間傳動軸的剛度，依此類推，表1給出了各計算單元原始計算參數。

動力傳動系統扭振固有頻率和振型數據見表2，振型向量見表3（歸一化處理）。

4.3旋翼動力傳動系統固有特性

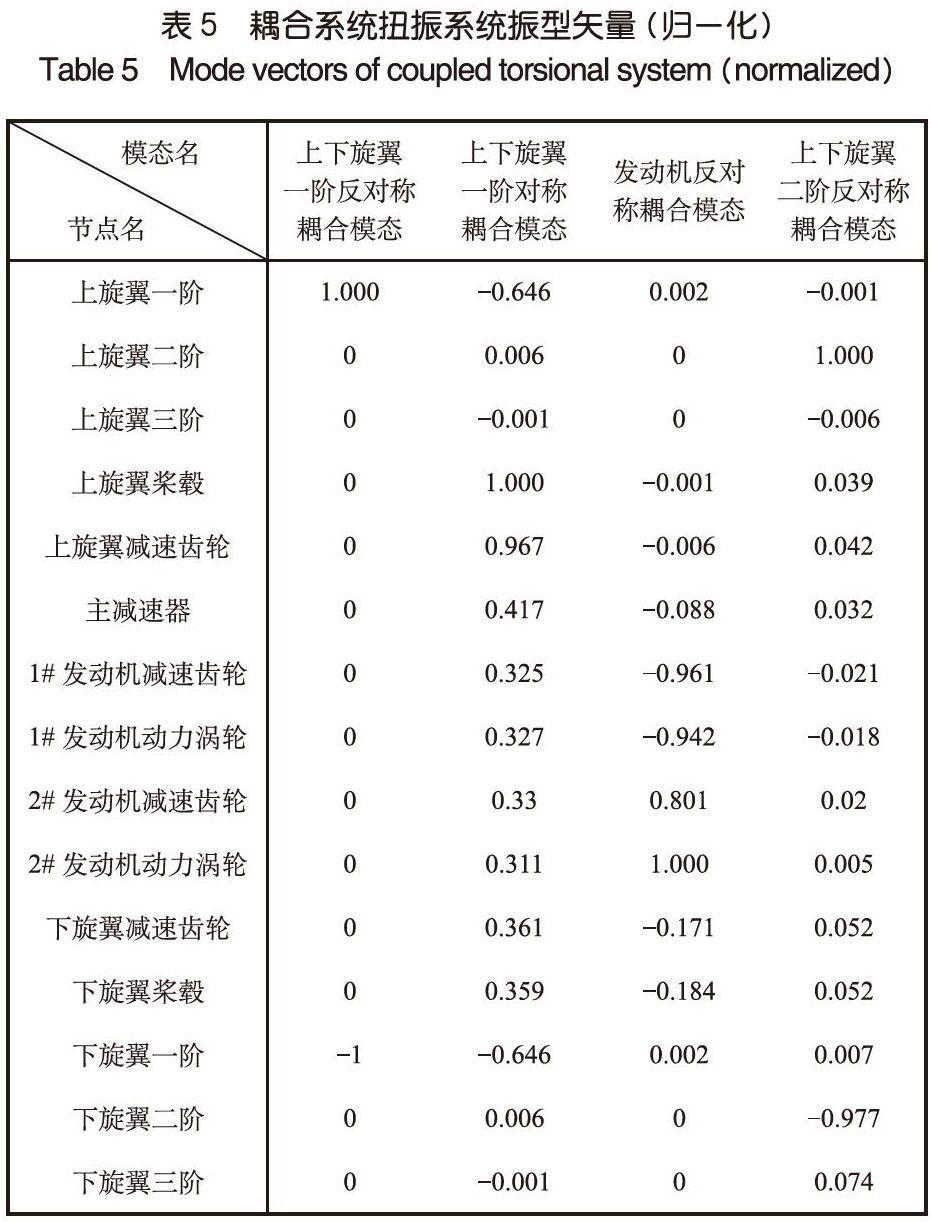
在前面計算孤立槳葉子系統擺振模態和傳動系統扭振模態的基礎上，考慮旋翼槳葉彈性，取槳葉擺振前三階模態、動力傳動系統扭振全部模態進行模態綜合，可以計算得到耦合扭振系統固有特性，計算100%升力、100%旋翼轉速狀態扭振系統固有特性，結果見表4。表5給出了表4所列計算結果的對應振型矢量（歸一化處理）。

5結束語

本文以共軸雙旋翼直升機為研究對象，分別建立了旋翼擺振集合性動力學分析模型以及動力傳動系統動力學分析模型，并以模態綜合法為基礎，綜合得到旋翼動力傳動系統扭振分析模型。通過算例進行驗證計算，總結共軸雙旋翼直升機扭振系統特性具有如下特點：

（1）不同于常規單旋翼帶尾槳式直升機扭振系統，共軸雙旋翼直升機扭振系統具有特有的扭振模態，如上、下兩幅旋翼之間，其耦合模態存在對稱、反對稱共存的特征。

（2）對于某種局部模態，如發動機反對稱模態，在耦合前后不受旋翼模態的影響。

（3）動力傳動系統與旋翼系統耦合后，耦合頻率較耦合前孤立槳葉的頻率更低。

本文僅計算了槳葉正常工作轉速下的扭振耦合特性，由于槳葉轉速由轉速0到100%轉速過程中，槳葉結構因離心力剛度不斷加強，槳葉結構頻率亦不斷提高，這種現象將導致不同階次模態耦合頻率發生不同的變化趨勢，這也將是后續共軸雙旋翼直升機扭振系統特性研究的重點。

總之，計算耦合狀態下旋翼動力傳動扭振系統的固有特性是很有必要的，計算所得到的耦合頻率可為后續分析扭振系統是否會與旋翼一階通過頻率接近從而導致較大強迫振動提供判據。該計算方法可用于直升機初步工程設計階段旋翼和動力傳動系統的優化設計。