基于Gibbs抽樣方法的空間滯后隨機前沿模型Bayesian估計
竇劍軍,王 媛,張輝國,胡錫健
(1.蘭州財經大學隴橋學院,蘭州 730101;2.新疆大學 數學與系統科學學院,烏魯木齊 830046)
0 引言
每個生產單元追求的是低投入高產出的利潤最大化,這就要求生產單元將技術效率發揮到最大化,對于每個生產單元面臨的問題是如何測算它們的技術效率。作為技術效率測算的參數方法的隨機前沿模型應運而生,該模型于 1977 年被 Meeusen[1],Aigner[2]與 Battese[3]提出后被廣泛地應用于諸多行業技術效率的測算中。經過四十多年的發展,一系列關于隨機前沿模型的設定和模型的參數估計方法、技術效率估計推斷以及將隨機前沿模型應用到具體行業測算技術效率的成果不斷出現,為每個行業技術效率的測算提供的一種全新的技術方法。
在隨機前沿模型發展的初期主要研究經典的隨機前沿模型,其假定不同的生產單元相互獨立。但是經濟、知識、技術效率往往具有空間上的溢出效應,技術效率高的生產單元將會集聚到一起,技術效率低的生產單元將會集聚到一起,形成“馬太效應”。所以,地理位置上的鄰接和經濟上的關聯是產生空間效應的重要因素。所以經典的隨機前沿模型在技術效率的測算過程中存在很大的缺陷。
近年來,隨著產業結構的調整,產業出現了集聚化的發展,生產單元與生產單元之間的聯系越來越緊密,空間交互效應發揮著重要的作用。將空間交互效應引入到經典隨機前沿模型中形成空間隨機前沿模型,其理論研究層出不窮并且將該方法應用具體行業的技術效率測算中。在模型參數估計方面,張進峰(2014)[4]應用二階段最小二乘法和矩估計方法對空間滯后隨機前沿模型作了估計。在應用方面,陳關聚(2014)[5]應用隨機前沿技術測算了中國制造業30個行業的全要素能源效率,張月玲等(2015)[6]應用隨機前沿模型研究了人力資本結構、適宜技術選擇與全要素生產率變動的分解,陳潔(2016)[7]應用隨機前沿模型測算了我國各省份用電技術效率。
上述估計方法可以得到模型參數的一致估計,但對參數的顯著性進行假設檢驗時檢驗統計量的構造比較困難。鑒于此,目前應用貝葉斯方法對空間滯后隨機前沿模型的參數做估計還沒有出現,本文用貝葉斯方法對模型參數的估計進行了研究。貝葉斯方法的最大優點在于得到了模型參數的后驗分布,在進行參數的顯著性假設檢驗時檢驗統計量比較容易得到。
1 模型介紹
考慮如下隨機前沿模型:

其中y是n個生產單元的產出構成的一個n×1維的向量,X是一個n×(m+1)的設計矩陣,由每個生產單元的m個投入構成的矩陣,W是n個單元的空間權重矩陣。v是不可控的隨機因素,設v~N(0,),u是技術無效率項,設u~N+(0,),v與u相互獨立,在u已知的條件下,y服從正態分布。
在模型(1)中待估計的參數為ρ,β,,和技術無效率項u,為了對參數進行貝葉斯估計,需要選擇參數的先驗分布。與的先驗分布選擇為倒Gamma分布,即取:
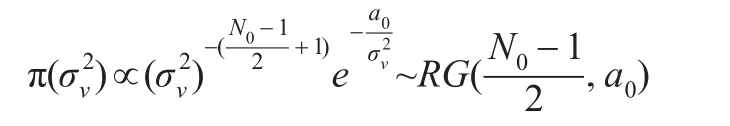
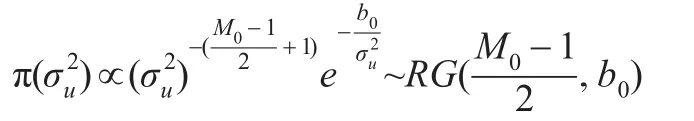
取ρ和β的先驗分布為:
π(β)∝const
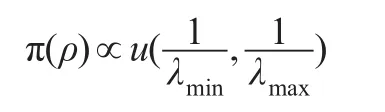
其中λmin,λmax為空間鄰接矩陣的最小特征值和最大特征值。
由y=ρWy+Xβ+v-u和u已知的條件下得v=(I-ρW)y+u-Xβ,根 據v~N(0,) 有所以
由貝葉斯公式,經計算得參數聯合后驗分布:
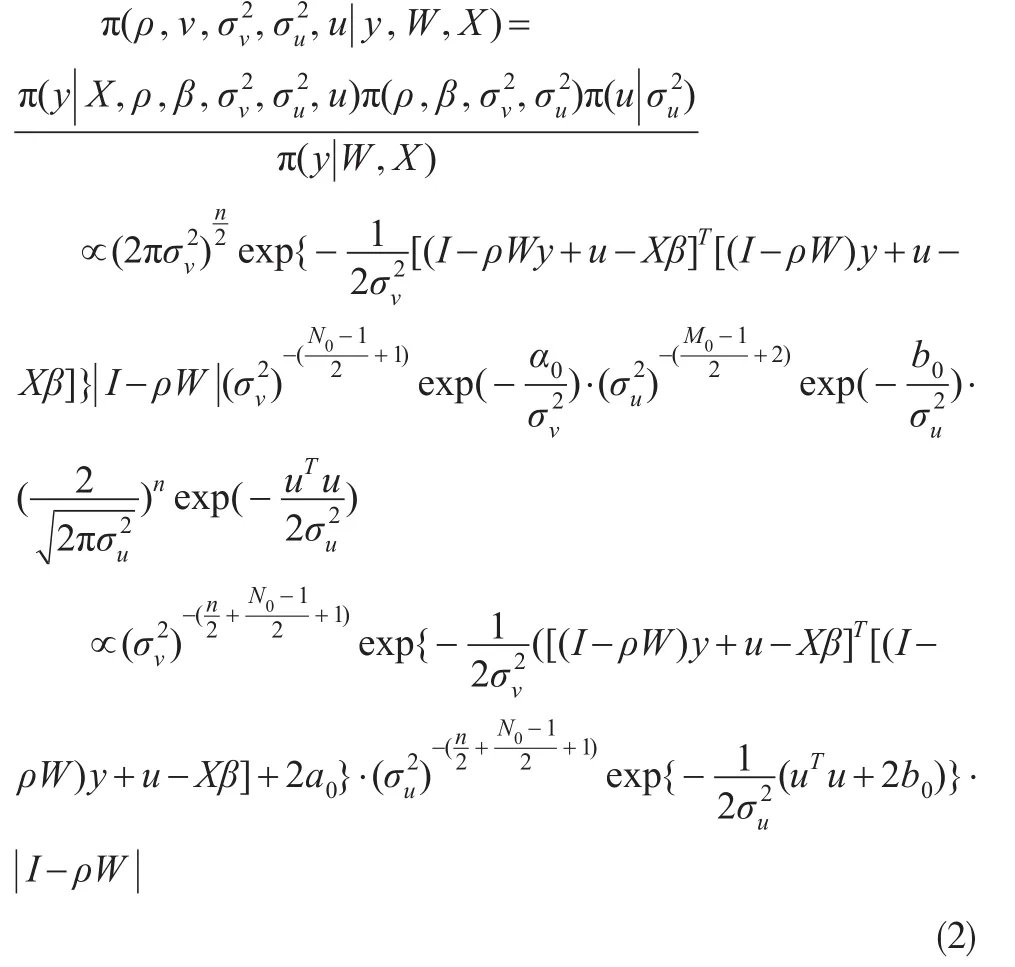
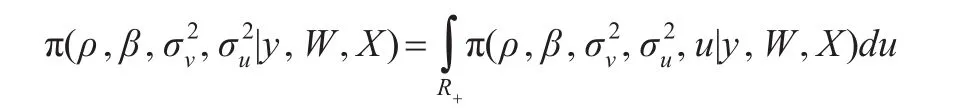
其中R+表示正實數。
從上可以得到,模型參數的聯合后驗分布是一個高維分布,得到每個參數的后驗分布需要對聯合后驗作積分,該積分有可能不存在或沒有辦法得到。基于此,將采用馬爾科夫鏈蒙特卡羅(MCMC)方法中的Gibbs抽樣方法對模型參數的后驗均值進行推斷。Gibbs抽樣是一種解決高維Bayesian模型的后驗積分困難問題的迭代Monte Carlo方法,它避免了對復雜表達式進行積分的問題。Gibbs抽樣得到的樣本{ρ(i),β(i),,,u(i);i=1,2,…n}隨著i的增大將會收斂到已知核的參數后驗分布。因此所有關于參數的向量函數的后驗期望可以通過Gibbs抽樣得到的樣本平均值來近似。即:
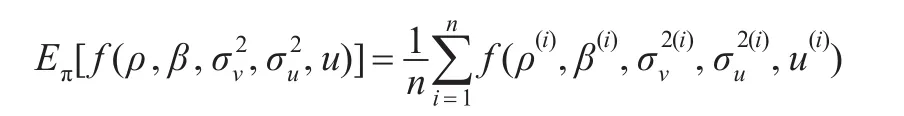
2 參數的條件分布及其抽樣方法
為了進行抽樣,首先需要推導出每個參數的后驗條件分布,在給定u的條件下,由公式(2)可以得到每個參數后驗條件分布的核。這里記D={y,W,X}。β的后驗條件分布為:
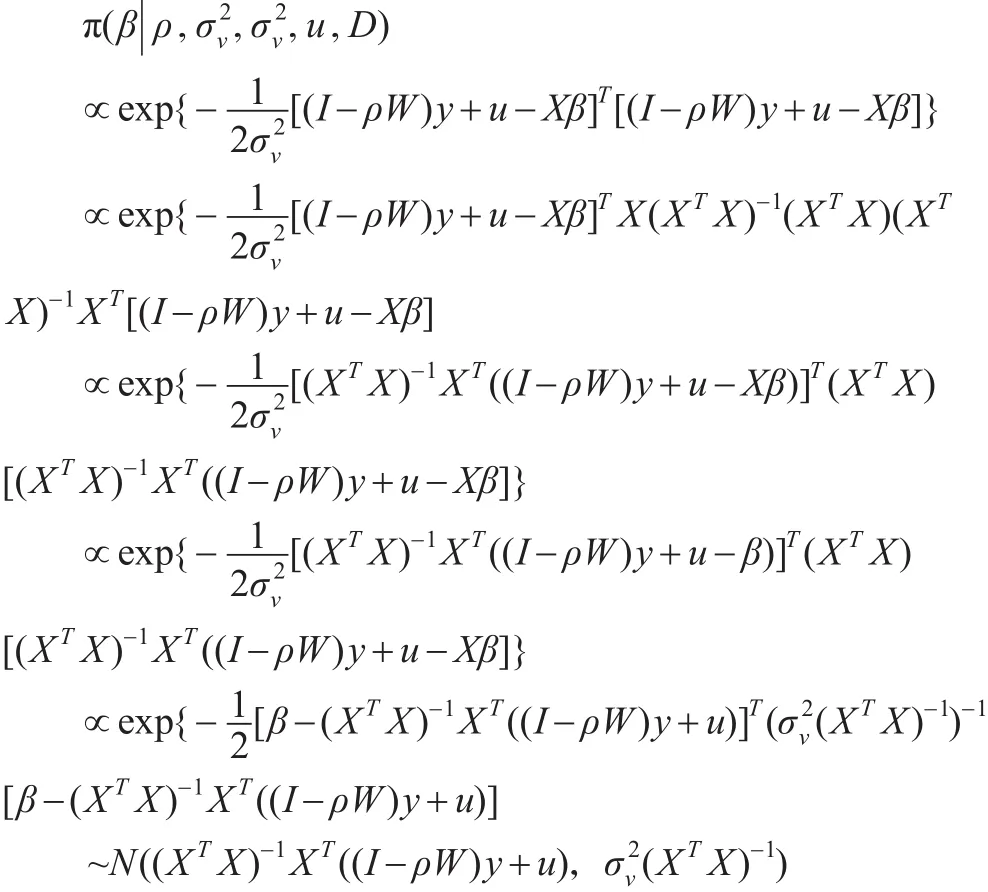
由上式可以看出β后驗條件分布為多元正態分布。
的后驗條件分布為:
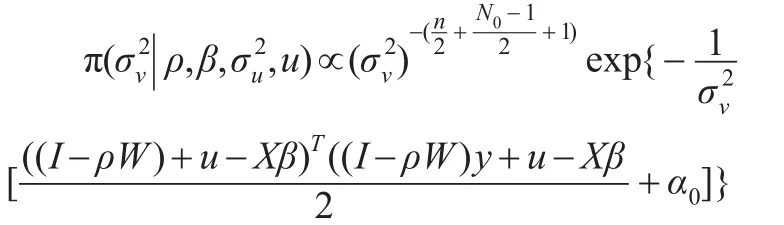
恰好為倒Gamma分布密度函數的核,即:
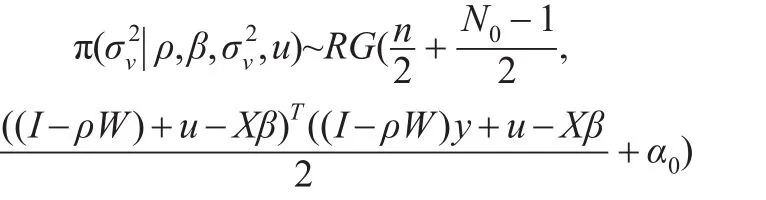
的后驗條件分布為:
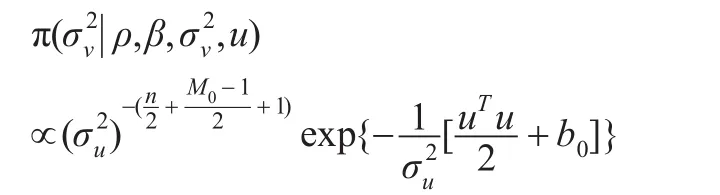
這恰好也為倒Gamma分布密度函數的核,即:
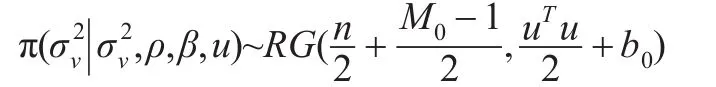
參數ρ的條件后驗分布為:
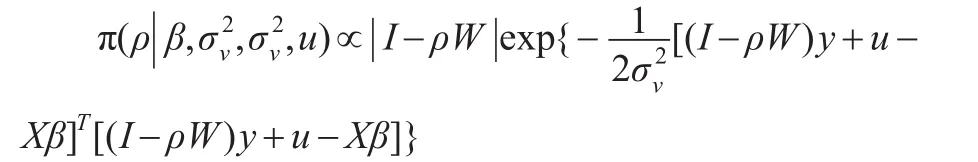
這個后驗條件分布不再是一個常見的分布形式,對參數ρ的抽樣需要采用Metropolis-Hastings方法(M-H)。對于M-H抽樣,需要一個建議分布,從中產生參數ρ的一個候選點,記為ρ*,將這個候選值與當前值ρc代入上式中去計算馬爾科夫鏈轉移概率:

假設ρ*從一個對稱的提議分布g(ρ*|ρc)=g(ρc|ρ*)中產生,則在每一次迭代中,從g(·)中產生一個增量Z,然后ρ*=ρc+Z,比如增量Z可以從標準正態分布中產生,此時候選點ρ*|ρc~N(ρc,σ2),σ2> 0
產生ρ的算法如下:
(1)構造合適的建議分布g(·|ρc);
(2)從 建 議 分 布g(·) 中 產 生 一 個 增 量 Z,令ρ*=ρc+Z;
(3)重復上述步驟(直到馬氏鏈達到平穩狀態)
(a)從 U(0,1)中產生 u;
(c)增加t,返回到(a)。
參數u的條件分布為:
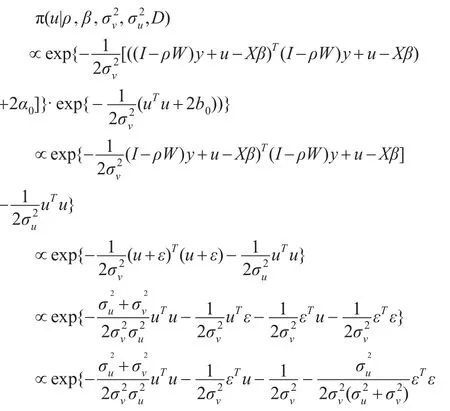
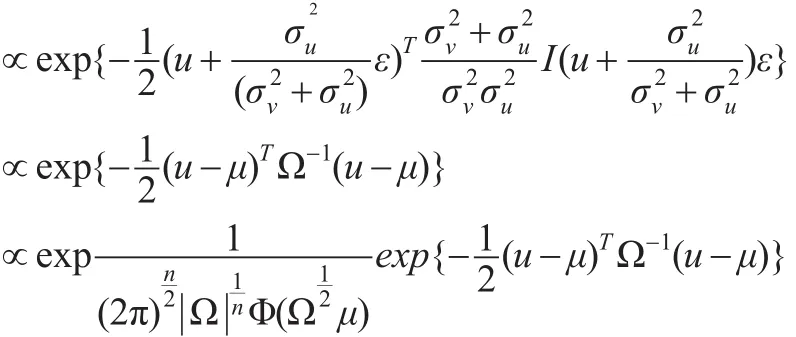
可見u的后驗條件分布服是n元截尾正態分布N+(μ,Ω),可直接對其進行抽樣。
3 技術效率的估計
Jondrow等(1982)[8]研究得到各個生產單元的技術無效率項ui可以通過E(ui|εi)或Mode(ui|εi)來測算,第i個生產單 元 的 技 術 效 率TEi=exp{-u?i} ,其 中=E(ui|εi) 或Mode(ui|εi)。因此,只要求得u的后驗條件分布的均值或眾數即可。因為u的后驗條件分布為截尾正態分布,所以
每個生產單元的技術效率為:
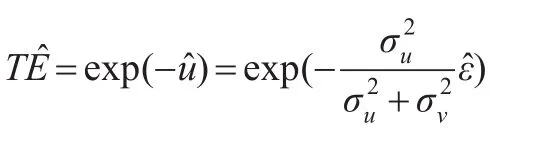
4 模特卡羅模擬
為了驗證解決Bayesian估計中高維積分問題的Gibbs抽樣方法的效果,本文進行了數值模擬,考慮如下數據生成過程:
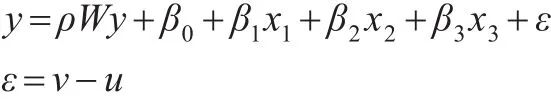
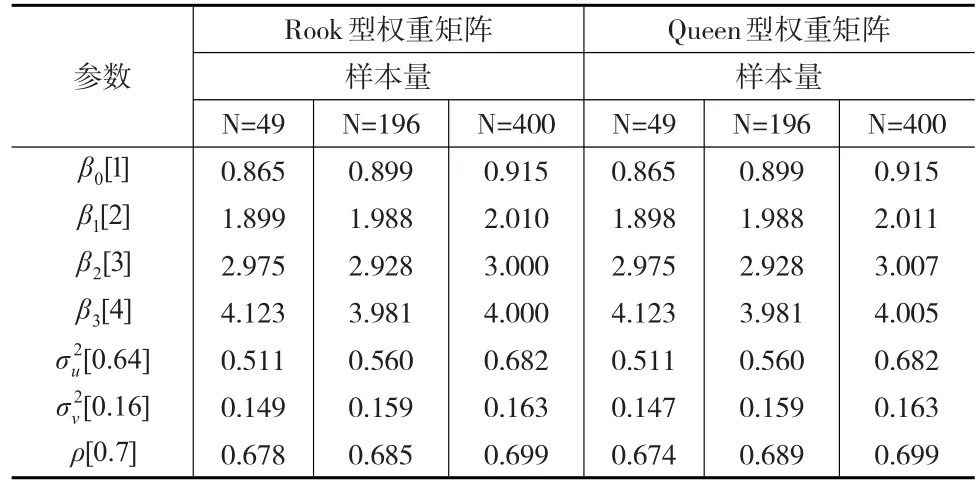
表1 參數后驗均值模擬結果
從表1可以看出,參數的模擬值非常接近真實值(其中第一列中括號里的為真實值),該方法在模擬過程中取得了比較好的效果,因此Bayesian方法能夠很好地對空間滯后隨機前沿模型作出估計。
5 結論與展望
本文基于Gibbs抽樣方法對空間滯后隨機前沿模型進行了Bayesian推斷,得到了模型參數的后驗條件分布和技術效率的估計。Gibbs抽樣方法是一種解決高維Bayesian模型積分問題的后驗迭代Monte Carlo方法,它避免了對聯合后驗分布進行數值積分計算的問題。模擬結果表明,參數的估計值不受空間權重矩陣的影響,并且估計值十分接近真實值。
本文僅考慮因變量的空間滯后,沒有考慮誤差的空間自相關。沿用本文的方法和思想,可以把該方法應用到到空間滯后誤差自相關隨機前沿模型的參數估計中。同時可以把技術無效率的分布擴展到指數分布、截尾正態分布等其他形式的分布。
參考文獻:
[1]Meeusen W,Broeck J V D.Effciency Estimation from Cobb-Douglas Production Functions With Composed Error[J].International Econom?ic Review,1977,(18).
[2]Aigner D,Lovell K,Schmidt P.Formulation and Estimation of Stochas?tic Frontier Production Function Models[J].Journal of Economet?rics,1977,(6).
[3]Battese G,Corra G.Estimation of a Production Frontier Model:With Application to the Pastoral Zone of Eastern Australia[J].Australian Journal of Agricultural Economics,1977,(21).
[4]張進峰.空間滯后隨機前沿模型的估計研究[J].商業經濟與管理,2014,(8).
[5]陳關聚.中國制造業全要素能源效率及影響因素研究——基于面板數據的隨機前沿分析[J].中國軟科學,2014,(1).
[6]張月玲,葉阿忠,陳泓.人力資本結構、適宜技術選擇與全要素變動分解——基于區域異質性隨機前沿生產函數的經驗分析[J].財經研究,2015,41(6).
[7]陳潔.我國用電技術的隨機前沿分析[J].生態經濟,2016,32(8).
[8]Jondrow J,Lovell K,Materov I,et al.On the Estimation of Technical Ineffciency in the Stochastic Frontier Production Function Model[J].Journal of Econometrics,1982,(19).

